Histoire des math??matiques
Contexte des ??coles Wikip??dia
Enfants SOS ont produit une s??lection d'articles de wikipedia pour les ??coles depuis 2005. Tous les enfants disponibles pour le parrainage de SOS Enfants des enfants sont pris en charge dans une maison de famille pr??s de la charit??. Lire la suite ...
| Histoire des sciences |
|---|
 |
Fond
|
Par ??poque
|
Par la culture
|
Sciences naturelles
|
Math??matiques
|
Sciences sociales
|
Technologie
|
M??decine
|
Pages de navigation
|
La zone d'??tude connu comme l'histoire des math??matiques est principalement une enqu??te sur l'origine de d??couvertes en math??matiques et, dans une moindre mesure, une enqu??te sur les m??thodes math??matiques et la notation du pass??.
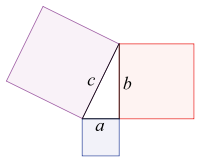
Avant l' ??re moderne et ?? la propagation dans le monde de la connaissance, des exemples ??crits de nouveaux d??veloppements math??matiques en sont venus ?? la lumi??re que dans quelques endroits. Les textes math??matiques les plus anciennes sont disponibles Plimpton 322 ( Babylonienne math??matiques c. 1900 avant JC), le Papyrus Math??matique Rhind (math??matiques ??gyptienne c. 2000-1800 BC) et le Papyrus de Moscou ( Math??matiques ??gyptiennes c. 1890 BC). Tous ces textes concernent la soi-disant th??or??me de Pythagore , qui semble ??tre le d??veloppement math??matique la plus ancienne et r??pandue apr??s l'arithm??tique de base et de la g??om??trie.
L'??tude des math??matiques comme un sujet ?? part enti??re commence dans le 6??me si??cle avant JC avec le Pythagoriciens, qui a invent?? le terme ??math??matiques?? de l'ancienne μάθημα grec (mathema), ce qui signifie ??sous r??serve de l'instruction". Math??matiques grecques grandement affin?? les m??thodes (en particulier par l'introduction de raisonnement d??ductif et rigueur math??matique dans preuves ) et ??largi l'objet de math??matiques. Math??matiques chinoises faites premi??res contributions, y compris une placer syst??me de valeurs. Le Syst??me de num??ration indo-arabe et les r??gles pour l'utilisation de ses op??rations, en usage dans le monde d'aujourd'hui, ont probablement ??volu?? au cours du premier mill??naire de notre ??re en Inde et a ??t?? transmise ?? l'ouest par les math??matiques islamiques. Math??matiques islamiques, ?? son tour, d??velopper et ??tendre les math??matiques connues de ces civilisations. Beaucoup de textes grecs et arabes sur les math??matiques ??taient alors traduit en latin, qui a conduit ?? la poursuite du d??veloppement des math??matiques dans l'Europe m??di??vale .
Depuis les temps anciens par les Moyen-Age , des ??clats de la cr??ativit?? math??matique ??taient souvent suivis par des si??cles de stagnation. ?? partir de la Renaissance en Italie au 16??me si??cle, de nouveaux d??veloppements math??matiques, en interaction avec de nouvelles d??couvertes scientifiques, ont ??t?? faites ?? un rythme croissant qui continue ?? travers le pr??sent jour.
Math??matiques pr??historique
L'origine de la pens??e math??matique se trouvent dans les concepts de nombre , l'ampleur et forme. Les ??tudes modernes de la cognition animale ont montr?? que ces concepts ne sont pas uniques ?? l'homme. Ces concepts auraient fait partie de la vie quotidienne dans les soci??t??s de chasseurs-cueilleurs. L'id??e de la notion de "Num??ro" ??volution progressivement au fil du temps est pris en charge par l'existence des langues qui pr??servent la distinction entre ??un??, ??deux??, et ??beaucoup??, mais pas de num??ros de plus de deux.
L'objet connu ??ventuellement math??matique la plus ancienne est le Lebombo os, d??couvert dans les montagnes Lebombo de Swaziland et dat?? ?? environ 35 000 en Colombie-Britannique. Il se compose de 29 crans distincts coup??es en p??ron?? de babouin. Aussi pr??historique artefacts d??couverts en Afrique et en France , dat??s entre 35 000 et Ancienne 20000 ann??es, sugg??rent les premi??res tentatives ?? quantifier le temps.
Le b??ton d'Ishango , trouv?? pr??s de la source du Nil rivi??re (nord-est du Congo ), peut-??tre autant que 20000 ann??es vieux et se compose d'une s??rie de marques de pointage sculpt??es en trois colonnes sur toute la longueur de l'os. Interpr??tations communes sont que l'os d'Ishango indique soit la premi??re manifestation connue de s??quences de nombres premiers ou un calendrier lunaire de six mois. Dans le livre Comment Math??matiques Happened: Les premiers 50 000 ans, Peter Rudman fait valoir que le d??veloppement de la notion de nombres premiers ne aurait pu se produire apr??s le concept de la division, qu'il remonte ?? 10 000 apr??s JC, avec des nombres premiers probablement pas ?? se faire comprendre jusqu'?? environ 500 BC. Il ??crit ??galement que ??aucune tentative n'a ??t?? faite pour expliquer pourquoi un d??compte de quelque chose doit pr??senter des multiples de deux nombres premiers, entre 10 et 20, et quelques chiffres qui sont presque des multiples de 10." Le b??ton d'Ishango, selon l'universitaire Alexander Marshack, peut avoir influenc?? le d??veloppement ult??rieur des math??matiques en Egypte, comme certaines entr??es sur l'os d'Ishango, l'arithm??tique ??gyptienne a ??galement fait usage de la multiplication par deux; Ceci, cependant, est contest??e.
Pr??dynastique Egyptiens de la 5??me mill??naire avant JC repr??sent??s graphiquement g??om??triques dessins. Il a ??t?? affirm?? que monuments m??galithiques de l'Angleterre et de l'Ecosse , datant du 3??me mill??naire avant JC, int??grent id??es g??om??triques telles que des cercles , ellipses , et Triplets pythagoriciens dans leur conception.
Tout ce qui pr??c??de sont contest??s cependant, et le plus ancien actuellement l'usage math??matique est incontest?? dans les sources ??gyptiennes et babyloniennes dynastiques. Ainsi, il a pris des ??tres humains au moins 45000 ann??es de la r??alisation des la modernit?? comportementale et de la langue (g??n??ralement consid??r??es comme un long moment avant que) de d??velopper les math??matiques en tant que tels.
Math??matiques babyloniennes
Babylonienne math??matiques se r??f??re ?? des math??matiques du peuple de la M??sopotamie (l'actuel Irak ) des jours du d??but des Sum??riens ?? travers le P??riode hell??nistique presque ?? l'aube du christianisme . Il est nomm?? math??matiques babyloniennes en raison du r??le central de Babylone comme un lieu d'??tude. Plus tard dans le cadre du Empire arabe, en M??sopotamie, en particulier ?? Bagdad , une fois de plus devenu un centre important d'??tude pour Math??matiques islamiques.
Contrairement ?? la raret?? des sources de Math??matiques ??gyptiennes, notre connaissance des math??matiques babyloniennes proviennent de plus de 400 tablettes d'argile d??terr??s depuis les ann??es 1850. ??crit en ??criture cun??iforme, les comprim??s ont ??t?? inscrits alors que l'argile ??tait humide, et cuit dur dans un four ou par la chaleur du soleil. Certains d'entre eux semblent ??tre class?? devoirs.
Les premi??res traces ??crites des math??matiques remonte aux anciens Sum??riens , qui ont construit la premi??re civilisation en M??sopotamie. Ils ont d??velopp?? un syst??me complexe de la m??trologie de 3000 BC. Depuis environ 2500 avant J.-C., les Sum??riens ??crit tables de multiplication sur des tablettes d'argile et trait??es g??om??triques exercices et division probl??mes. Les premi??res traces des chiffres babyloniens datent aussi de cette p??riode.
La majorit?? des tablettes d'argile r??cup??r??s datent de 1800 ?? 1600 avant JC, et couvrent des sujets qui comprennent fractions, alg??bre, ??quations du second degr?? et de cubes, et le calcul des r??gulier r??ciproque paires. Les comprim??s comprennent ??galement des tables et des m??thodes pour r??soudre multiplication lin??aire et ??quations du second degr?? . La tablette babylonienne YBC 7289 donne une approximation de √2 pr??cise ?? cinq d??cimales.
Les math??matiques babyloniennes ont ??t?? ??crites en utilisant un sexag??simal (base-60) de syst??me de num??ration . De l?? d??coule l'utilisation moderne de jour de 60 secondes dans une minute, 60 minutes ?? une heure, et 360 (60 x 6) degr??s dans un cercle, ainsi que l'utilisation des secondes et minutes d'arc pour d??signer fractions de degr??. Progr??s en math??matiques babyloniennes ont ??t?? facilit??es par le fait que 60 a de nombreux diviseurs. En outre, contrairement aux Egyptiens, les Grecs et les Romains, les Babyloniens avaient un syst??me de valeur de vrai, o?? chiffres ??crits dans la colonne de gauche repr??sentaient des valeurs plus grandes, autant que dans la d??cimale syst??me. Ils ne avaient pas, cependant, un ??quivalent de la virgule, et ainsi de la valeur de position d'un symbole souvent d?? ??tre d??duite du contexte. D'autre part, ce ??d??faut?? est ??quivalent ?? l'utilisation moderne de l'arithm??tique flottante; En outre, l'utilisation de la base 60 signifie que ne importe quel r??ciproque d'un nombre entier qui est un multiple de diviseurs de 60 a n??cessairement un d??veloppement limit?? ?? la base 60. (En arithm??tique d??cimale, seuls inverses des multiples de 2 et 5 ont des d??veloppements d??cimaux finis. ) En cons??quence, il ya un argument fort que l'arithm??tique babylonienne style ancien est beaucoup plus sophistiqu?? que celui de l'usage courant.
L'interpr??tation de Plimpton 322 ??tait la source de controverse depuis de nombreuses ann??es apr??s sa signification dans le contexte de triangles de Pythagore a ??t?? r??alis??. Dans le contexte historique, les probl??mes de succession impliquant cloisonnement ??gal zone de champs triangulaires et trap??zo??dales (avec des c??t??s entiers de longueur) convertissent rapidement dans la n??cessit?? de calculer la racine carr??e de 2, ou pour r??soudre ??l'??quation de Pythagore" en nombres entiers: plut??t que de consid??rer un place que la somme de deux carr??s, nous pouvons envisager de fa??on ??quivalente un carr?? comme une diff??rence de deux carr??s. Apr??s la division, (ca) (c + a) = bb devient le produit de deux nombres rationnels donnant une: (c / ba / b) (c / b + a / b) = 1. Ceci est facilement r??solu par consultation d'une table des paires r??ciproques. Les solutions de l'??quation originale sont ainsi param??tr??es par le choix d'un nombre rationnel x, d'o??-triangles rectangles de Pythagore triple peuvent facilement ??tre construits en entier d??tartrage un triangle rectangle dont les c??t??s mesurent 2x longueur, xx-1, xx + 1 (si un d??sir de math??maticien contemporain de le faire). Tous les triplets pythagoriciens se posent dans ce chemin, et les exemples fournis dans Plimpton 322 impliquent certains assez grand nombre, selon les normes modernes, tels que (4601, 4800, 6649) dans la notation d??cimale.
Math??matiques ??gyptiennes
??gyptienne math??matiques se r??f??re aux math??matiques ??crites dans le Langue ??gyptienne. Du P??riode hell??nistique, grec remplac?? ??gyptienne comme langue ??crite de ??rudits ??gyptiens. Etude math??matique dans l'Egypte a continu?? tard dans le cadre du Empire arabe dans le cadre de Math??matiques islamiques, o?? l'arabe est devenu la langue ??crite de savants ??gyptiens.
Le plus vaste texte math??matique ??gyptienne est la Papyrus Rhind (parfois aussi appel?? le Ahm??s Papyrus de son auteur), dat?? c. 1650 avant JC, mais probablement une copie d'un document plus ancien de la Moyen-Uni d'environ 2000-1800 av. Ce est un manuel d'instruction pour les ??l??ves de l'arithm??tique et de la g??om??trie. En plus de donner des formules et des m??thodes de multiplication, division r??gion et de travailler avec des fractions de l'unit??, il contient ??galement des preuves d'autres connaissances math??matiques, y compris composites et nombres premiers ; arithm??tique , g??om??trique et des moyens harmoniques; et compr??hensions simplistes ?? la fois du Crible d'??ratosth??ne et la th??orie des nombres parfaits (?? savoir que le nombre de six). Il montre ??galement comment r??soudre de premier ordre des ??quations lin??aires ainsi que arithm??tique et s??rie g??om??trique.
Un autre texte math??matique ??gyptienne importante est la Papyrus de Moscou, ??galement de la P??riode du Moyen Empire, dat?? c. 1890 BC. Il se compose de ce que sont aujourd'hui appel?? probl??mes de mots ou des probl??mes de l'histoire, qui ??taient apparemment destin??s comme un divertissement. Un probl??me est consid??r?? comme ??tant d'une importance particuli??re car elle donne une m??thode pour trouver le volume d'un tronc: "Si on vous dit:. Une pyramide tronqu??e de 6 pour la hauteur verticale de 4 sur la base de 2 sur le haut Vous ??tes ?? la quadrature du 4, entra??ner 16. Vous ??tes ?? doubler 4, le r??sultat 8. Vous ??tes ?? carr?? 2, entra??ner 4. Vous ??tes pour ajouter le 16, le 8 et le 4, entra??ner 28. Vous ??tes de prendre un tiers des 6, entra??ner 2. Vous ??tes de prendre 28 deux fois, entra??ner 56. Voir, ce est 56 . Vous trouverez les choses. "
Enfin, la Berlin papyrus (c. 1300 BC) montre que les anciens Egyptiens pourrait r??soudre un second ordre ??quation alg??brique.
Math??matiques grecques
Math??matiques grecques se r??f??re aux math??matiques ??crites dans la langue grecque de l'??poque de Thal??s de Milet (~ 600 avant JC) ?? la fermeture de la Acad??mie d'Ath??nes en 529 AD. Math??maticiens grecs vivaient dans des villes r??parties sur l'ensemble de la M??diterran??e orientale, de l'Italie ?? l'Afrique du Nord, mais ont ??t?? unis par la culture et la langue. Math??matiques grecques de la p??riode suivant Alexandre le Grand est parfois appel?? math??matiques hell??nistiques.
Math??matiques grecques ??tait beaucoup plus sophistiqu?? que les math??matiques qui ont ??t?? ??labor??s par les cultures ant??rieures. Tous les dossiers survivants des math??matiques pr??-grecs montrent l'utilisation du raisonnement inductif, ce est observations r??p??t??es utilis??s pour ??tablir des r??gles de pouce. Math??maticiens grecs, en revanche, utilis??s raisonnement d??ductif. Les Grecs utilisaient la logique de tirer des conclusions ?? partir des d??finitions et des axiomes, et utilis??s rigueur math??matique ?? prouver eux.
Math??matiques grecques est pens?? pour avoir commenc?? avec Thal??s de Milet (c. 624-c.546 BC) et Pythagore de Samos (c. 582-c. 507 BC). Bien que l'ampleur de l'influence est contest??e, ils ont probablement ??t?? inspir??s par ??gyptienne et Les math??matiques babyloniennes. Selon la l??gende, Pythagore a voyag?? en Egypte pour apprendre les math??matiques, la g??om??trie, l'astronomie et de pr??tres ??gyptiens.
Thales utilis?? la g??om??trie pour r??soudre des probl??mes tels que le calcul de la hauteur des pyramides et la distance des navires de la c??te. Il est cr??dit?? de la premi??re utilisation du raisonnement d??ductif appliqu?? ?? la g??om??trie, en d??rivant quatre corollaires Le th??or??me de Thal??s. En cons??quence, il a ??t?? salu?? comme le premier vrai math??maticien et l'individu d'abord connu ?? qui une d??couverte math??matique a ??t?? attribu??. Pythagore a ??tabli le ??cole de Pythagore, dont la doctrine ??tait que les math??matiques exclure l'univers et dont la devise ??tait ??Tout est nombre??. Ce ??tait les Pythagoriciens, qui a invent?? le terme ??math??matiques??, et avec lesquels l'??tude des math??matiques pour elle-m??me commence. Les pythagoriciens sont cr??dit??s de la premi??re preuve de la th??or??me de Pythagore , si la d??claration du th??or??me a une longue histoire, et la preuve de l'existence de nombres irrationnels .
Platon (428/427 BC - BC 348/347) est important dans l'histoire des math??matiques pour inspirer et guider les autres. Son Acad??mie de Platon, dans Ath??nes , est devenu le centre math??matique du monde dans le 4??me si??cle avant JC, et ce est de cette ??cole que les principaux math??maticiens de l'??poque, tels que Eudoxe de Cnide, est venu. Platon a ??galement examin?? les fondements des math??matiques, a pr??cis?? certaines des d??finitions (par exemple celle d'une ligne comme "longueur sans largeur"), et r??organis?? les hypoth??ses. La m??thode analytique est attribu?? ?? Platon, tout en une formule pour obtenir triplets pythagoriciens porte son nom.
Eudoxe (408-c.355 BC) a d??velopp?? le m??thode de l'??puisement, un pr??curseur du moderne int??gration et une th??orie de rapports qui ont ??vit?? le probl??me de grandeurs incommensurables . L'ancien permis aux calculs de superficies et des volumes de figures curvilignes, tandis que le second a permis g??om??tres ult??rieures de faire des avanc??es significatives dans la g??om??trie. Bien qu'il n'a pas fait de d??couvertes math??matiques techniques sp??cifiques, Aristote (384-c.322 BC) a contribu?? de mani??re significative au d??veloppement des math??matiques en jetant les bases de la logique .
Dans le 3??me si??cle avant JC, le premier centre de l'??ducation et de la recherche math??matique ??tait le Musaeum d' Alexandrie . Ce est l?? que Euclid (c. 300 BC) a enseign??, et a ??crit le Elements , largement consid??r?? comme le manuel le plus de succ??s et les plus influents de tous les temps. Les ??l??ments introduits rigueur math??matique ?? travers le m??thode axiomatique et est le premier exemple du format encore utilis?? en math??matiques aujourd'hui, celle de la d??finition, axiome, th??or??me, et la preuve. Bien que la plupart des contenus des ??l??ments ??taient d??j?? connus, Euclid les rangea dans un seul cadre logique, coh??rente. Les ??l??ments ??tait connu pour tous les gens instruits en Occident jusqu'au milieu du 20e si??cle et son contenu est toujours enseign??e dans les classes de g??om??trie aujourd'hui. En plus des th??or??mes familiers de la g??om??trie euclidienne , des ??l??ments a ??t?? con??u comme un manuel d'introduction ?? tous les sujets math??matiques de l'??poque, tels que la th??orie des nombres , l'alg??bre et une g??om??trie solide, y compris des preuves que la racine carr??e de deux est irrationnel et qu'il existe une infinit?? de nombres premiers. Euclid aussi a beaucoup ??crit sur d'autres sujets, tels que les sections coniques , l'optique , g??om??trie sph??rique, et de la m??canique, mais seulement la moiti?? de ses ??crits survivent.
Le premier math??maticien femme enregistr??e par l'histoire ??tait Hypatie d'Alexandrie (AD 350-415). Elle a succ??d?? ?? son p??re comme biblioth??caire ?? la Grande Biblioth??que et a ??crit de nombreux ouvrages sur les math??matiques appliqu??es. Parce qu'elle ??tait une femme, la communaut?? chr??tienne ?? Alexandrie l'a punie pour sa pr??somption en d??shabillant et gratter sa peau avec des coquilles (certains disent tuiles).
Archim??de (c.287-212 BC) de Syracuse, largement consid??r?? comme le plus grand math??maticien de l'Antiquit??, utilis?? le Proc??d?? d'??puisement de calculer l' aire sous un arc de avec la parabole sommation d'une s??rie infinie, d'une mani??re pas trop diff??rente de calcul moderne. Il a ??galement montr?? on pourrait utiliser la m??thode de l'??puisement pour calculer la valeur de π avec autant de pr??cision que d??sir??, et a obtenu la valeur la plus pr??cise de π alors connu, 3 10/71 <π <3 10/70. Il a ??galement ??tudi?? la spirale qui porte son nom, obtint des formules pour les volumes de surfaces de r??volution (parabolo??de, ellipso??de, hyperbolo??de), et un syst??me ing??nieux pour exprimer un tr??s grand nombre. Alors qu'il est ??galement connu pour ses contributions ?? la physique et plusieurs dispositifs m??caniques avanc??es, Archim??de se pla??a valeur beaucoup plus grande sur les produits de sa pens??e et les principes math??matiques g??n??rales. Qu'il consid??rait comme sa plus grande r??alisation de son constat de la surface et le volume d'une sph??re, qu'il a obtenu en prouvant ce sont 2/3 de la surface et le volume d'un cylindre circonscrit ?? la sph??re.
Apollonius de Perge (c. 262-190 BC) a fait des progr??s importants ?? l'??tude des sections coniques , en montrant que l'on peut obtenir tous les trois vari??t??s de section conique en faisant varier l'angle de l'avion qui coupe un c??ne double-molletonn??e. Il a ??galement invent?? la terminologie en usage aujourd'hui pour les sections coniques, ?? savoir parabole ("placer ?? c??t??" ou "comparaison"), "ellipse" ("carence"), et "hyperbole" ("un jet au-del??"). Son travail de coniques est une des ??uvres les plus connues et les math??matiques conserv??s de l'antiquit??, et en elle il tire de nombreux th??or??mes concernant les sections coniques qui prouveraient une valeur inestimable pour les math??maticiens et astronomes qui ??tudient tard le mouvement des plan??tes, comme Isaac Newton. Bien que ni Apollonius ni d'autres math??maticiens grecs ont fait le saut ?? la g??om??trie analytique, le traitement d'Apollonius de courbes est en quelque sorte similaire au traitement moderne, et une partie de son travail semble anticiper le d??veloppement de la g??om??trie analytique par Descartes quelque 1800 ans plus tard.
Vers la m??me ??poque, Eratosth??ne de Cyr??ne Cyr??ne (c. 276-194 BC) a con??u le Crible d'??ratosth??ne pour trouver des nombres premiers . Le 3??me si??cle avant JC est g??n??ralement consid??r?? comme le "Golden Age" des math??matiques grecques, avec des avanc??es en math??matiques pures d??sormais en d??clin relatif. N??anmoins, dans les si??cles qui ont suivi des progr??s significatifs ont ??t?? r??alis??s en math??matiques appliqu??es, notamment la trigonom??trie , en grande partie pour r??pondre aux besoins des astronomes. Hipparque de Nic??e (c. 190-120 BC) est consid??r?? comme le fondateur de la trigonom??trie pour compiler la table trigonom??trique d'abord connu, et lui est ??galement due ?? l'utilisation syst??matique de la cercle de 360 degr??s. H??ron d'Alexandrie (c. 10-70 AD) est cr??dit?? La formule de H??ron pour trouver l'aire d'un triangle scal??ne et d'??tre le premier ?? reconna??tre la possibilit?? de nombres n??gatifs poss??dant des racines carr??es. M??n??las d'Alexandrie (c. 100 AD) pionnier trigonom??trie sph??rique travers Th??or??me de M??n??la??s. Le travail le plus complet et le plus influent de l'antiquit?? trigonom??trique est le Almageste de Ptol??m??e (c. AD 90-168), un trait?? d'astronomie historique dont les tables trigonom??triques serait utilis?? par les astronomes pour les mille prochaines ann??es. Ptol??m??e est ??galement cr??dit?? Th??or??me de Ptol??m??e pour d??river des quantit??s trigonom??triques, et la valeur la plus pr??cise de π ext??rieur de la Chine jusqu'?? la p??riode m??di??vale, 3,1416.
Apr??s une p??riode de stagnation apr??s Ptol??m??e, la p??riode entre 250 et 350 AD est parfois appel?? le ??Silver Age" des math??matiques grecques. Au cours de cette p??riode, Diophante r??alis?? des progr??s significatifs dans l'alg??bre , en particulier analyse ind??termin??e, qui est ??galement connu comme ??l'analyse diophantienne". L'??tude de ??quations diophantiennes et Approximations diophantiennes est un domaine important de la recherche ?? ce jour. Son travail principal ??tait l'Arithmetica, une collection de 150 probl??mes alg??briques traiter avec des solutions exactes pour d??termin??e et ??quations ind??termin??es. Le Arithmetica eu une influence significative sur les math??maticiens plus tard, comme Pierre de Fermat , qui est arriv?? ?? son c??l??bre dernier th??or??me apr??s avoir essay?? de g??n??raliser un probl??me qu'il avait lu dans le Arithmetica (que de diviser un carr?? en deux carr??s). Diophante a ??galement fait des progr??s significatifs dans la notation, le Arithmetica ??tant la premi??re instance du symbolisme alg??brique et la syncope.
Math??matiques chinoises
Early math??matiques chinois est si diff??rent de celui des autres parties du monde qu'il est raisonnable de supposer d??veloppement ind??pendant. Le plus ancien texte math??matique existant de la Chine est le Chou Pei Suan Ching, diversement dat?? entre 1200 avant JC et 100 avant JC, si une date d'environ 300 avant JC semble raisonnable.
On notera en particulier l'utilisation en math??matiques chinois d'un syst??me de notation positionnelle d??cimale, les soi-disant ??chiffres de tige" dans laquelle des chiffres distincts ont ??t?? utilis??s pour les nombres entre 1 et 10, et des chiffres suppl??mentaires pour les puissances de dix. Ainsi, le nombre 123 seraient ??crits en utilisant le symbole "1", suivi par le symbole ??100??, le symbole de "2" suivi par le symbole de "10", suivi par le symbole "3". Ce ??tait le syst??me de nombre le plus avanc?? dans le monde ?? l'??poque, apparemment en utiliser plusieurs si??cles avant l'??re commune et bien avant le d??veloppement du syst??me de num??ration indienne. num??ros de tige ont permis ?? la repr??sentation des nombres aussi grands que les calculs souhait??s et autoris??s ?? ??tre effectu??s sur la pan Suan ou boulier chinois. La date de l'invention de la casserole de Suan ne est pas certain, mais le premier ??crit dates mention de l'an 190, dans les notes compl??mentaires de Xu Yue sur l'art de figures.
Le plus ancien ouvrage existant sur la g??om??trie en Chine provient de la philosophie Mohist canon c. 330 BC, compil?? par les adeptes de Mozi (470-390 BC). Le Mo Jing d??crit divers aspects de nombreux domaines li??s ?? la science physique, et a fourni un petit nombre de th??or??mes g??om??triques ainsi.
En 212 avant JC, l'empereur Qin Shi Huang (Shi Huang-ti) commandait tous les livres dans l'Empire Qin autres que celles officiellement reconnues ??tre br??l??s. Ce d??cret n'a pas ??t?? universellement ob??i, mais comme une cons??quence de cet ordre peu est connu sur anciens math??matiques chinoises avant cette date. Apr??s le autodaf?? de 212 avant JC, la Dynastie des Han (202 BC-220 AD) produit des ??uvres des math??matiques qui vraisemblablement ??tendus sur les ??uvres qui sont aujourd'hui perdus. Le plus important d'entre eux est Les Neuf Chapitres sur l'art math??matique, le titre complet de ce qui semblaient par AD 179, mais existait en partie sous d'autres titres au pr??alable. Il se compose de 246 probl??mes comportant agriculture, les affaires, l'emploi de la g??om??trie de comprendre trav??es de hauteur et des rapports de dimensions pour Tours de pagode chinoise, de l'ing??nierie, arpentage, et comprend significatif sur triangles rectangles et les valeurs de π . Il a cr???? la preuve math??matique pour le th??or??me de Pythagore , et une formule math??matique pour l'??limination de Gauss . Liu Hui a comment?? sur le travail dans le 3??me si??cle apr??s JC, et a donn?? une valeur de π pr??cision de 5 d??cimales. Bien que plus d'une question d'endurance calcul que aper??u th??orique, dans le 5??me si??cle apr??s JC Zu Chongzhi calcul?? la valeur de π ?? sept d??cimales, qui est rest?? la valeur la plus pr??cise de π pr??s les prochaines 1000 ann??es. Il a ??galement ??tabli une m??thode qui sera plus tard appel?? M??thode des indivisibles de trouver le volume d'une sph??re .
La ligne des hautes eaux de math??matiques chinoises se produit au 13??me si??cle (derni??re partie de la p??riode Sung ), avec le d??veloppement de l'alg??bre chinoise. Le texte le plus important de cette p??riode est le Miroir pr??cieux des quatre ??l??ments par Chu Shih-chieh (fl. 1280-1303), qui traite de la solution d'??quations simultan??es ??lev??s alg??briques de commande en utilisant une m??thode similaire ?? La m??thode de Horner. Le Miroir pr??cieux contient ??galement un sch??ma de triangle de Pascal avec des coefficients de l'expansion binomiale par la huiti??me puissance, bien que les deux apparaissent dans les ouvrages chinois d??s 1100. La Chine a ??galement utilis?? du sch??ma combinatoire complexe connu sous le carr?? magique et cercles magiques, d??crites dans l'antiquit?? et au point par Yang Hui (AD 1238-1298).
M??me apr??s les math??matiques europ??ens ont commenc?? ?? se ??panouir au cours de la Renaissance , les math??matiques europ??ennes et chinoises ??taient traditions distinctes, avec sortie math??matique chinoise significative en d??clin du 13??me si??cle. Missionnaires j??suites tels que Matteo Ricci effectu??e id??es math??matiques et-vient entre les deux cultures du 16e au 18e si??cles, mais ?? ce point des id??es beaucoup plus math??matiques entraient dans la Chine de laisser.
Math??matiques indiennes
La premi??re civilisation sur le sous-continent indien est la civilisation de l'Indus qui a prosp??r?? entre 2600 et 1900 avant JC dans le fleuve Indus bassin. Leurs villes ont ??t?? am??nag??s avec une r??gularit?? g??om??trique, mais pas de documents math??matiques connus survivent de cette civilisation.
Les plus anciens documents math??matiques existants de l'Inde sont les Sulba soutras (dat??es diversement entre le 8??me si??cle avant JC et le 2??me si??cle apr??s JC), les annexes aux textes religieux qui donnent des r??gles simples pour construire des autels de diff??rentes formes, comme des carr??s, des rectangles, des parall??logrammes, et autres. Comme avec l'Egypte, la pr??occupation avec les fonctions du temple souligne ?? une origine des math??matiques dans le rituel religieux. Les soutras Sulba donnent des m??thodes pour construire une cercle avec approximativement la m??me surface d'un carr?? donn??, ce qui implique plusieurs approximations diff??rentes de la valeur de π . En outre, ils calculent la racine carr??e de 2 ?? plusieurs d??cimales, la liste des triples de Pythagore, et de donner une d??claration du th??or??me de Pythagore . Tous ces r??sultats sont pr??sents dans les math??matiques babyloniennes, indiquant influence m??sopotamienne. On ne sait pas dans quelle mesure les soutras Sulba influenc?? math??maticiens indiens tard. Comme en Chine, il ya un manque de continuit?? dans les math??matiques indiennes; des avanc??es significatives sont s??par??es par de longues p??riodes d'inactivit??.
Pāṇini (c. 5??me si??cle avant JC) a formul?? les r??gles de Grammaire sanskrit. Sa notation ??tait semblable ?? la notation math??matique moderne, et utilis?? m??tar??gles, transformations, et r??cursivit??. Pingala (environ 3??me-1??re si??cles avant JC) dans son trait?? de prosodie utilise un appareil correspondant ?? un syst??me de num??ration binaire . Sa discussion des combinatoire de m correspond ?? une version ??l??mentaire de la bin??me. Le travail de Pingala contient ??galement les id??es de base de nombres de Fibonacci (appel?? mātrāmeru).
Les prochains documents math??matiques importants de l'Inde apr??s les soutras Sulba sont les Siddhantas, trait??s d'astronomie de la 4e et 5e si??cles de notre ??re ( P??riode Gupta) montrant une forte influence hell??nistique. Ils sont importants en ce qu'ils contiennent de la premi??re instance de relations trigonom??triques en fonction de la demi-corde, comme ce est le cas dans la trigonom??trie moderne, plut??t que l'accord complet, comme ce fut le cas dans la trigonom??trie ptol??ma??que. Gr??ce ?? une s??rie d'erreurs de traduction, les mots "sinus" et "cosinus" d??coulent de la "jiya" sanskrit et "Kojiya".
Dans le 5??me si??cle apr??s JC, Aryabhata ??crit la Aryabhatiya, un volume mince, ??crite en vers, destin?? ?? compl??ter les r??gles de calcul utilis??s en astronomie et en mensuration math??matique, mais avec aucun sentiment pour la logique ou la m??thode d??ductive. Bien que pr??s de la moiti?? des entr??es sont mauvais, ce est dans le Aryabhatiya que le syst??me de valeur de d??cimale appara??t en premier. Plusieurs si??cles plus tard, le Math??maticien musulman Abu Rayhan Biruni d??crit le Aryabhatiya comme un ??m??lange de cailloux communs et cristaux co??teuses".
Au 7??me si??cle, Brahmagupta identifi?? le Brahmagupta th??or??me, L'identit?? et Brahmagupta Formule de Brahmagupta, et pour la premi??re fois, en Brahma-sphuta-siddhanta, il lucidement expliqu?? l'utilisation de z??ro ?? la fois comme un espace r??serv?? et d??cimale , et explique le Syst??me de num??ration indo-arabe. Il ??tait d'une traduction de ce texte indienne sur les math??matiques (c. 770) que les math??maticiens islamiques ont ??t?? introduits ?? ce syst??me num??rique, qui ils se sont adapt??s que les chiffres arabes . ??rudits islamiques effectu??es connaissance de ce syst??me num??rique pour l'Europe par le 12??me si??cle, et il est maintenant d??plac??e tous les syst??mes num??riques ??g??es ?? travers le monde. Au 10??me si??cle, Le commentaire de Halayudha sur Le travail de Pingala contient une ??tude de la suite de Fibonacci et le triangle de Pascal , et d??crit la formation d'une matrice .
Au 12??me si??cle, Bhāskara II vivait dans le sud de l'Inde et a beaucoup ??crit sur toutes les branches des math??matiques alors connus. Son travail contient des objets math??matiques ou ??quivalent approximativement ??quivalent ?? infinit??simaux, d??riv??s, le th??or??me de la valeur moyenne et la d??riv??e de la fonction sinus. Dans quelle mesure il a anticip?? l'invention du calcul est un sujet de controverse parmi les historiens des math??matiques.
Au 14??me si??cle, Madhava de Sangamagrama, le fondateur de la soi-disant Kerala ??cole de math??matiques, a trouv?? la S??rie Madhava-Leibniz, et, en utilisant 21 termes, calcul?? la valeur de π que 3,14159265359. Madhava ??galement trouv?? la s??rie Madhava-Gr??goire de d??terminer l'arctangente, le Newton-Madhava s??rie de puissance pour d??terminer sinus et cosinus et le rapprochement Taylor pour les fonctions sinus et cosinus. Au 16??me si??cle, Jyesthadeva consolid?? un grand nombre de d??veloppements et les th??or??mes de l'??cole dans le Kerala Yukti-Bhasa. Toutefois, l'??cole Kerala n'a pas formul?? une th??orie syst??matique de la diff??renciation et de l'int??gration , il ne existe aucune preuve directe de leurs r??sultats transmis ?? l'ext??rieur Kerala. Progr??s en math??matiques ainsi que d'autres domaines de la science a stagn?? en Inde avec la cr??ation de La domination musulmane en Inde.
Math??matiques islamique
Le Empire islamique ??tablis ?? travers la Perse , le Moyen-Orient , Asie centrale, Afrique du Nord , Iberia, et dans certaines parties de l'Inde dans le 8??me si??cle apport?? d'importantes contributions math??matiques. Bien que la plupart des textes islamiques sur les math??matiques ont ??t?? ??crits en arabe , la plupart d'entre eux ne ont pas ??t?? ??crits par des Arabes , depuis peu comme le statut de la langue grecque dans le monde hell??nistique, l'arabe a ??t?? utilis?? comme langue ??crite de chercheurs non-arabes dans l'ensemble du monde islamique ?? la temps. Perses contribu?? au monde de math??matiques aux c??t??s des Arabes.
Au 9??me si??cle, le Math??maticien persan Al-Khwarismi a ??crit plusieurs livres importants sur les chiffres indo-arabes et sur les m??thodes de r??solution des ??quations. Son livre Sur le calcul avec chiffres hindous , écrit environ 825, avec le travail de Al-Kindi, ont joué un rôle dans la diffusion des mathématiques indiennes et chiffres indiens à l'Ouest. Le mot algorithme est dérivée de la latinisation de son nom, Algoritmi, et le mot algèbre dans le titre d'une de ses ??uvres, Al-Kitab al-Mukhtasar fî al-hisab Gabr wal-muqabala ( Le Livre Compendious sur le calcul par Achèvement et équilibrage ). Il a donné une explication exhaustive de la solution algébrique des équations du second degré avec racines positives, et il fut le premier à enseigner l'algèbre dans une forme élémentaire et pour son propre bien. Il a également discuté de la méthode fondamentale de « réduction »et« équilibre », se référant à la transposition des termes soustraits à l'autre côté de l'équation, qui est, l'annulation des termes comme sur les côtés opposés de l'équation. Ceci est l'opération qui al-Khwarizmi décrit à l'origine comme al-Jabr . Son algèbre était aussi plus concerné "avec une série de problèmes à résoudre, mais une exposition qui commence avec les termes primitifs dont les combinaisons doivent donner tous les prototypes possibles pour les équations, qui constituent désormais explicitement le véritable objet de l'étude. " Il a également étudié une équation pour son propre bien et "de manière générique, dans la mesure où il ne ressort pas tout simplement dans le cadre de la résolution d'un problème, mais est spécifiquement appelé à définir une classe infinie de problèmes."
D'autres développements dans l'algèbre ont été faites par Al-Karaji dans son traité al-Fakhri , où il étend la méthodologie pour intégrer les puissances entières et les racines entières de quantités inconnues. Quelque chose à proximité d'une preuve par induction mathématique apparaît dans un livre écrit par Al-Karaji autour de 1000 AD, qui sert à prouver la formule du binôme, triangle de Pascal , et la somme des intégrales cubes. Le historien des mathématiques, F. Woepcke, a salué Al -Karaji pour être "le premier qui a introduit la théorie de la algébrique le calcul . " Toujours dans le 10ème siècle, Abul Wafa traduit les ??uvres de Diophante en arabe. Ibn al-Haytham a été le premier mathématicien pour calculer la formule pour la somme des puissances quatrièmes, en utilisant une méthode qui est facilement généralisable pour déterminer la formule générale pour le somme de toutes les puissances entières. Il a effectué une intégration afin de trouver le volume d'un paraboloïde, et a été en mesure de généraliser son résultat pour les intégrales des polynômes jusqu'au quatrième degré. Il est venu ainsi près de trouver une formule générale pour les intégrales de polynômes, mais il n'a pas été préoccupé par des polynômes de plus que la quatrième degré.
Dans la fin du 11ème siècle, Omar Khayyam a écrit discussions des difficultés à Euclid , un livre sur ce qu'il percevait comme des failles dans d'Euclide éléments , en particulier le postulat des parallèles. Il a également été le premier à trouver la solution géométrique générale des équations cubiques. Il a également été très influent dans la réforme du calendrier.
Au 13??me si??cle, Nasir al-Din al-Tusi (Nasireddin) a fait des progrès dans la trigonométrie sphérique. Il a également écrit ouvrage influent sur ??????les Euclid s ' postulat des parallèles. Au 15??me si??cle, Ghiyath al-Kashi calculé la valeur de ?? à la 16e décimale. Kashi a également eu un algorithme de calcul n ième racines, ce qui était un cas particulier des méthodes indiquées nombreux siècles plus tard par Ruffini et Horner.
Autres réalisations de mathématiciens musulmans pendant cette période comprennent l'ajout de lanotation décimale pour leschiffres arabes, la découverte de tous les modernesfonctions trigonométriquesen plus le sinus,l'introduction d'al-Kindi decryptanalyse etla fréquence d'analyse, le développement dela géométrie analytiqueparIbn al-Haytham, le début dela géométrie algébrique parOmar Khayyam et le développement d'unenotation algébrique paral-Qalasadi.
Pendant le temps de l'Empire ottomanetsafavide Empire du 15ème siècle, le développement des mathématiques islamiques est devenu stagnant.
Mathématiques médiévale européenne
Intérêt européen médiéval en mathématiques a été alimentée par des préoccupations tout à fait différentes de celles des mathématiciens modernes. Un élément de conduite était la croyance que les mathématiques à condition que la clé pour comprendre l'ordre créé de la nature, justifie souvent par Platon de Timée et le passage biblique (dans le Livre de la Sagesse ) que Dieu avait ordonné à tous les choses dans la mesure, et le nombre, et poids .
Boèce a fourni un endroit pour les mathématiques dans le curriculum au 6ème siècle quand il a inventé le terme quadrivium pour décrire l'étude de l'arithmétique, la géométrie, l'astronomie et la musique. Il a écrit De institutione arithmetica , une traduction libre du grec de de Nicomaque Introduction à l'arithmétique ; De institutione musica , également dérivé de sources grecques; et une série d'extraits de Euclide s ' Elements . Ses ??uvres étaient théoriques, plutôt que pratique, et sont à la base de l'étude des mathématiques jusqu'à la reprise des travaux mathématiques grecs et arabes.
Au 12ème siècle, les savants européens ont voyagé à l'Espagne et de la Sicileà la recherche de textes arabes scientifiques, y comprisal-Khwarizmis ' Le Compendious livre sur le calcul par l'achèvement et l'équilibrage, traduit en latin parRobert de Chester, et le texte complet ded'EuclideElements, traduits en différentes versions parAdelard de Bath,Herman de Carinthie, etGérard de Crémone.
Ces nouvelles sources ont suscité un renouveau des mathématiques. Fibonacci, écrivant dans le Liber Abaci , en 1202 et mis à jour en 1254, a produit le premier mathématiques importantes en Europe depuis l'époque de Eratosthène, un écart de plus de mille ans. Le travail présenté des chiffres indo-arabes en Europe, et a discuté de nombreux autres problèmes mathématiques.
Le 14e siècle a vu le développement de nouveaux concepts mathématiques pour enquêter sur un large éventail de problèmes. Une contribution importante a été le développement des mathématiques du mouvement local.
Thomas Bradwardine proposé que la vitesse (V) augmente en proportion arithmétique comme le rapport de la force (F) à la résistance (R) augmente en proportion géométrique. Bradwardine exprimé cela en une série d'exemples spécifiques, mais bien que le logarithme avait pas encore été conçu, nous pouvons exprimer sa conclusion anachronique par écrit: V = log (F / R). L'analyse de Bradwardine est un exemple de transfert d'une technique mathématique utilisée par Al-Kindi et Arnaud de Villeneuve à quantifier la nature des médicaments composés d'un problème physique différent.
Un de la 14e siècleOxford Calculatrices,William Heytesbury, manquantcalcul différentiel et la notion delimites, a proposé de mesurer la vitesse instantanée "par le chemin quiseraitêtre décrit par [un organisme]si... il était transféré uniformément à la même degré de rapidité avec laquelle il est déplacé à cet instant donné ".
Heytesbury et d'autres mathématiquement déterminé la distance parcourue par un corps subissant mouvement uniformément accéléré (aujourd'hui résolu parl'intégration), en déclarant que "un corps en mouvement uniforme acquérir ou perdre cet incrément [la vitesse] va traverser dans quelques temps donné une [Distance] complètement égal à celle qu'elle aurait si elle était traverser déplace en continu à travers le même temps avec le degré moyen [de vitesse] ".
Nicole Oresme à l' Université de Paris et l'Italien Giovanni di Casali fourni indépendamment des démonstrations graphiques de cette relation, affirmant que l'aire sous la ligne représentant l'accélération constante, représentait la distance totale parcourue. Dans un commentaire mathématique plus tard d'Euclide Eléments , Oresme a fait une analyse générale plus détaillée dans laquelle il a démontré que le corps va acquérir dans chaque tranche successive de temps un incrément de toute qualité qui augmente à mesure que les nombres impairs. Depuis Euclide avait démontré la somme des nombres impairs sont les nombres carrés, la qualité totale acquise par les corps augmente comme le carré de l'époque.
Mathématiques Renaissance
Pendant la Renaissance , le développement des mathématiques et de la comptabilité ont été liés. Bien qu'il n'y ait pas de relation directe entre l'algèbre et de la comptabilité, l'enseignement des sujets et les livres publiés souvent destiné aux enfants de marchands qui ont été envoyés à compter écoles (en Flandre et l'Allemagne ) ou boulier écoles (connu sous le nom abbaco en Italie), où ils ont appris les compétences utiles pour le commerce et le commerce. Il n'y a probablement pas besoin de l'algèbre dans l'exécution des opérations comptables, mais pour les opérations de troc complexes ou le calcul de l'intérêt composé, une connaissance de base de l'arithmétique était obligatoire et la connaissance de l'algèbre a été très utile.
Luca Pacioli "Summa de Arithmetica, Geometria, Proportioni et Proportionalità" (en italien: «Examen de l'arithmétique , la géométrie , Ratio et Proportion ") premier a été imprimées et publiées dans de Venise en 1494. Il comprenait un 27 pages Trait?? sur comptabilité, "Particularis de Computis et Scripturis " (en italien: «Détails du calcul et d'enregistrement»). Il a été écrit principalement pour, et vendue principalement, les commerçants qui ont utilisé le livre comme un texte de référence, comme une source de plaisir des énigmes mathématiques qu'il contenait, et à une aide à l'éducation de leurs fils. Dans Summa Arithmetica , Pacioli introduit des symboles pour plus et moins pour la première fois dans un livre imprimé, des symboles qui sont devenus notation standard en mathématiques de la Renaissance italienne. Summa Arithmetica était aussi le premier livre imprimé en Italie connue pour contenir l'algèbre . Il est important de noter que Pacioli avait lui-même emprunté une grande partie de l'??uvre de Piero Della Francesca qu'il plagié.
En Italie, au cours de la première moitié du 16ème siècle, Scipione del Ferro et Niccolò Fontana Tartaglia ont découvert des solutions pour les équations cubiques. Gerolamo Cardano les a publiées dans son livre 1545 Ars Magna , avec une solution pour les équations du quatrième degré, découvert par son élève Lodovico Ferrari. En 1572, Rafael Bombelli publié son L'algèbre dans lequel il a montré comment traiter avec les quantités imaginaires qui pourraient apparaître dans la formule de Cardano pour résoudre des équations cubiques.
Le livre de Simon StevinDe thiende(«l'art de dixièmes '), d'abord publié en néerlandais en 1585, contenait le premier traitement systématique denotation décimale, qui a influencé tous les travaux plus tard sur lesystème des nombres réels.
Poussé par les exigences de la navigation et le besoin croissant de cartes précises de grandes zones,la trigonométriea grandi pour être une branche majeure de mathématiques.Bartholomaeus Pitiscus était le premier à utiliser le mot, la publication de sonTrigonometriaen 1595. tableau de Regiomontanus des sinus et cosinus a été publié en 1533.
Pendant la Renaissance le désir des artistes pour représenter le monde naturel de façon réaliste, avec la philosophie retrouvée des Grecs, conduit les artistes à étudier les mathématiques. Ils étaient aussi les ingénieurs et les architectes de cette époque, et avait donc besoin des mathématiques dans tous les cas. L'art de la peinture en perspective, et les développements en géométrie impliqués, ont été étudiés intensément.
Mathématiques au cours de la révolution scientifique
17??me si??cle
Le 17e siècle a vu une explosion sans précédent des idées mathématiques et scientifiques en Europe. Travers Galileo a observé les lunes de Jupiter en orbite autour de cette planète, en utilisant un télescope basé sur un jouet importé de Hollande. Tycho Brahe avait rassemblé une énorme quantité de données mathématiques décrivant le positions des planètes dans le ciel. Grâce à sa position comme l'assistant de Brahe, Johannes Kepler a d'abord été exposé à et sérieusement interagi avec le thème de mouvement planétaire. Les calculs de Kepler ont été simplifiées par l'invention contemporaine de logarithmes par John Napier et Jost Bürgi. Kepler a réussi à formuler des lois mathématiques du mouvement planétaire. La géométrie analytique développé par René Descartes (1596-1650) a permis à ces orbites à être reportés sur un graphique, en coordonnées cartésiennes . Simon Stevin (1585) a créé la base pour la notation décimale moderne capable de décrire tous les numéros, si rationnelle ou irrationnelle.
Construire sur des travaux antérieurs par de nombreux prédécesseurs, Isaac Newton a découvert les lois de la physique expliquant les lois de Kepler , et a réuni les concepts maintenant connu comme calcul infinit??simal. Indépendamment, Gottfried Wilhelm Leibniz a développé le calcul et une grande partie de la notation de calcul encore en usage aujourd'hui. Sciences et les mathématiques étaient devenus une entreprise internationale, qui allait bientôt se répandre sur le monde entier.
En plus de l'application des mathématiques à des études sur les cieux, mathématiques appliquées commencé à se développer dans de nouveaux domaines, avec la correspondance de Pierre de Fermat et de Blaise Pascal . Pascal et Fermat jeté les bases pour les enquêtes de la théorie des probabilités et les règles correspondantes de la combinatoire dans leurs discussions sur un jeu de jeu. Pascal, avec son pari, tenté d'utiliser la théorie des probabilités nouveau développement à plaider en faveur d'une vie consacrée à la religion, sur la motif que, même si la probabilité de succès était faible, les récompenses étaient infinies. Dans un certain sens, cela préfigure le développement de la théorie de l'utilité dans le 18e au 19e siècle.
18??me si??cle
Le mathématicien le plus influent du 18ème siècle était sans doute Leonhard Euler . Ses contributions vont de la fondation de l'étude de la théorie des graphes avec les sept ponts de Königsberg problème de la normalisation de nombreux termes et des notations mathématiques modernes. Par exemple, il a nommé la racine carrée de moins 1 avec le symbole i , et il a popularisé l'utilisation de la lettre grecque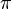 
pour représenter le rapport de la circonférence d'un cercle à son diamètre. Il a fait de nombreuses contributions à l'étude de la topologie, la théorie des graphes, le calcul, la combinatoire, et l'analyse complexe, comme en témoigne la multitude de théorèmes et de notations nommés pour lui.
Autres mathématiciens européens importants du 18ème siècle inclusJoseph Louis Lagrange, qui a fait ??uvre de pionnier dans la théorie des nombres, l'algèbre, le calcul différentiel, et le calcul des variations, etLaplacequi, à l'âge deNapoléon, ont fait un travail important sur ??????les fondations decéleste la mécanique et sur??????les statistiques.
Mathématiques modernes
19??me si??cle
Tout au long du 19e siècle les mathématiques sont devenus de plus en plus abstraite. Au 19ème siècle vécu Carl Friedrich Gauss (1777-1855). Laissant de côté ses nombreuses contributions à la science, en mathématiques pures qu'il a fait un travail révolutionnaire sur les fonctions de variables complexes, à la géométrie , et sur ??????la convergence des s??rie. Il a donné les premières preuves satisfaisantes du théorème fondamental de l'algèbre et de la la loi de r??ciprocit?? quadratique.
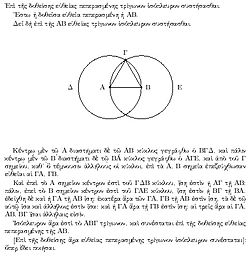
Ce siècle a vu le développement des deux formes de la géométrie non-euclidienne, où le postulat parallèle de la géométrie euclidienne ne tient plus. Le mathématicien russe Nikolaï Ivanovitch Lobatchevski et son rival, le mathématicien hongrois János Bolyai, définis indépendamment et étudié la géométrie hyperbolique, où l'unicité de parallèles ne tient plus. Dans cette géométrie la somme des angles d'un triangle ajouter jusqu'à moins de 180 °. géométrie elliptique a été développé plus tard dans le 19ème siècle par le mathématicien allemand Bernhard Riemann ; ici pas d'équivalent peut être trouvé et les angles d'un triangle ajouter jusqu'à plus de 180 °. Riemann a également développé la géométrie de Riemann, qui unifie et généralise largement les trois types de géométrie, et il a défini le concept d'un collecteur , qui généralise les idées de courbes et surfaces.
Le 19ème siècle a vu le début d'une grande partie de l'algèbre abstraite . Hermann Grassmann en Allemagne a donné une première version du espaces vectoriels , William Rowan Hamilton en Irlande développé l'algèbre non commutative. Le mathématicien britannique George Boole a conçu une algèbre qui a vite évolué dans ce qui est maintenant appelé l'algèbre de Boole, dans lequel les seuls chiffres étaient de 0 et de 1. algèbre de Boole est le point de départ de la logique mathématique et a d'importantes applications dans l'informatique .
Augustin-Louis Cauchy,Bernhard Riemann, etKarl Weierstrass reformulées le calcul d'une manière plus rigoureuse.
Aussi, pour la première fois, les limites des mathématiques ont été explorées. Niels Henrik Abel, un Norvégien, et Évariste Galois, un Français, ont prouvé qu'il n'y a pas de méthode algébrique générale pour résoudre des équations algébriques de degré supérieur à quatre ( Abel-Ruffini théorème ). Autres mathématiciens du 19ème siècle utilisé ce dans leurs preuves que la règle et compas sont seuls ne suffisent pas à la trisection un angle arbitraire, pour construire le côté d'un cube deux fois le volume d'un cube donné, ni pour construire une égale carrés dans la zone à une donnée cercle. Mathématiciens avaient vainement tenté de résoudre tous ces problèmes depuis l'époque des Grecs anciens. D'autre part, la limitation des trois dimensions de la géométrie a été dépassé dans le 19ème siècle par des considérations de l'espace des paramètres et des numéros hypercomplexes.
Les enquêtes d'Abel et de Galois dans les solutions de diverses équations polynomiales ont jeté les bases de nouveaux développements de la théorie des groupes , et les domaines connexes de l'algèbre abstraite . Au 20e siècle, les physiciens et d'autres scientifiques ont vu la théorie des groupes comme le moyen idéal pour étudier la symétrie .
À la fin du 19ème siècle, Georg Cantor a établi les premiers fondements de la théorie des ensembles , ce qui a permis le traitement rigoureux de la notion de l'infini et est devenu la langue commune de presque tous les mathématiques. La théorie des ensembles de Cantor, et la montée de la logique mathématique dans les mains de Peano, LEJ Brouwer, David Hilbert , Bertrand Russell , et AN Whitehead, a lancé un débat long de roulement sur ??????la fondements des math??matiques.
Le 19ème siècle a vu la création d'un certain nombre de sociétés mathématiques nationales: laLondon Mathematical Society en 1865, laSociété Mathématique de France en 1872, leCircolo Matematico di Palermo en 1884, laSociété mathématique d'Edimbourg en 1883, et de l'American Mathematical Society 1888. La première, la société d'intérêt spécial international, laSociété Quaternion, a été formé en 1899, dans le contexte d'unecontroverse de vecteur.
En 1897, Hensel introduitnombres p-adiques.
20i??me si??cle
Le 20e siècle a vu les mathématiques deviennent une profession importante. Chaque année, des milliers de nouveaux titulaires d'un doctorat en mathématiques sont attribués, et les emplois sont disponibles dans l'enseignement et l'industrie.
Dans un discours de 1900 à l' Congrès international des mathématiciens, David Hilbert a établi une liste de 23 problèmes non résolus en mathématiques. Ces problèmes, couvrant de nombreux domaines des mathématiques, ont formé un point central pour une grande partie des mathématiques 20e siècle. Aujourd'hui, 10 ont été résolus, 7 sont partiellement résolus, et 2 sont encore ouverts. Les 4 autres sont trop lâche formulé pour être déclaré comme résolu ou non.
Conjectures historiques notables ont finalement été prouvés. En 1976, Wolfgang Haken et Kenneth Appel utilisé un ordinateur pour prouver la théorème des quatre couleurs . Andrew Wiles, se fondant sur ??????le travail des autres, a prouvé le dernier théorème de Fermat en 1995. Paul Cohen et Kurt Gödel a démontré que l' hypothèse de continuum est indépendant de (possible être ni prouvée ni réfutée à partir de) les axiomes standard de la théorie des ensembles. En 1998, Thomas Hales Callister prouvé la conjecture de Kepler.
Collaborations mathématiques de la taille et la portée sans précédent ont eu lieu. Un exemple est le classification des groupes finis simples (également appelés la «énorme théorème"), dont la preuve entre 1955 et 1983 requise articles de revues quelque 500 d'environ 100 auteurs, et des dizaines de remplissage de milliers de pages. Un groupe de mathématiciens français, dont Jean Dieudonné et André Weil, de l'édition sous le pseudonyme de " Nicolas Bourbaki ", a tenté de Exposit toutes les mathématiques connues comme un tout cohérent rigoureuse. Les plusieurs dizaines de volumes résultant a eu une influence controversée sur l'enseignement des mathématiques.
Géométrie différentielle est venu dans son propre quand Einstein a utilisé dans la relativité générale . Nouvelles zones entières des mathématiques tels que la logique mathématique, topologie , et John von Neumann de la théorie des jeux changé les types de questions qui pourraient être résolues par des méthodes mathématiques. Tous les types de structures ont été extraites en utilisant axiomes et prénoms, comme les espaces métriques, espaces topologiques, etc. Comme font les mathématiciens, la notion d'une structure abstraite était elle-même abstraite et ont conduit à th??orie des cat??gories. Grothendieck et Serre refonte géométrie algébrique en utilisant la théorie de la gerbe. Les grandes avancées ont été faites dans l'étude qualitative des systèmes dynamiques que Poincaré avait commencé dans les années 1890. Mesurer la théorie a été développée à la fin du 19ème et début du 20ème siècles. Applications de mesures comprennent l' intégrale de Lebesgue , l'axiomatisation de Kolmogorov de la théorie des probabilités et la théorie ergodique. Nouez théorie considérablement élargi. La mécanique quantique a conduit au développement d' analyse fonctionnelle. autres domaines nouveaux comprennent, de Laurent Schwarz la théorie de distribution, théorie des points fixes, la th??orie des singularit??s et de René Thom la théorie des catastrophes, modèle la théorie et de Mandelbrot les fractales . théorie de Lie avec ses groupes de Lie et algèbres de Lie est devenu l'un des principaux domaines d'étude.
L'analyse non-standard, introduit par Abraham Robinson, rehabillitated l' approche au calcul infinitésimal, qui était tombé en discrédit en faveur de la théorie de limites , en étendant le champ des nombres réels pour les numéros hyperréaliste qui comprennent des quantités infimes et infinies. Un système de nombre encore plus important, les chiffres surréalistes ont été découvert par John Horton Conway dans le cadre de jeux combinatoires.
Le développement et l'amélioration continue des ordinateurs , au premières machines mécaniques analogiques, puis les machines électroniques numériques, a permis l'industrie pour faire face à des quantités plus en plus grandes de données pour faciliter la production et la distribution et la communication de masse, et de nouveaux domaines des mathématiques ont été élaborés pour faire face à cette : Alan Turing s ' théorie de la calculabilité; théorie de la complexité; de Claude Shannon théorie de l'information; traitement du signal; l'analyse des données; optimisation et d'autres domaines de la recherche opérationnelle . Dans les siècles précédents beaucoup l'accent mathématique était sur ??????le calcul et fonctions continues, mais la montée des réseaux informatiques et de communication a conduit à une importance croissante des concepts distincts et l'expansion de la combinatoire , y compris la th??orie des graphes. les capacités de vitesse et de traitement de données d'ordinateurs a également permis à la manipulation de mathématique problèmes qui étaient beaucoup trop de temps à traiter par papier et crayon calculs, conduisant à des domaines tels que l'analyse numérique et calcul symbolique. Certains des procédés les plus importants et les algorithmes du 20ème siècle sont: l' algorithme du simplexe, la transformée de Fourier rapide, les codes correcteurs d'erreurs, le filtre de Kalman à partir de la théorie du contrôle et de l' algorithme RSA de cryptographie ?? cl?? publique.
Dans le même temps, des idées profondes ont été faites sur les limites aux mathématiques. En 1929 et 1930, il a été prouvé la vérité ou la fausseté de toutes les déclarations formulées sur les nombres naturels plus un des additions et des multiplications, était décidable, ce pourrait être déterminée par un algorithme. En 1931, Kurt Gödel a constaté que ce ne fut pas le cas pour le naturel numéros plus deux addition et de multiplication; ce système, connu sous le nom arithmétique de Peano, était en fait inachevable. (Arithmétique de Peano est adéquate pour une bonne partie de la théorie des nombres , y compris la notion de nombre premier .) Une conséquence de deux de Gödel théorèmes d'incomplétude est que dans tout système mathématique qui inclut l'arithmétique de Peano (y compris l'ensemble des analyses et géométrie ), la vérité devance nécessairement la preuve, à savoir qu'il ya de vrais déclarations qui ne peuvent pas être prouvés au sein du système. Ainsi les mathématiques ne peut être réduite à la logique mathématique, et David Hilbert rêve de faire de toutes les mathématiques complètes et cohérentes nécessaires pour être reformulé.
Une des figures les plus colorés en mathématiques 20e siècle était Srinivasa Ramanujan Aiyangar (1887-1920), un Indien autodidacte qui a conjecturé ou avéré plus de 3000 théorèmes, y compris les propriétés des nombres très composites, la fonction de partition et ses asymptotique et fonctions thêta maquettes . Il a également fait des enquêtes majeures dans les domaines de fonctions gamma, formes modulaires, séries divergentes, séries hypergéométriques et nombre premier théorie.
Paul Erd??s a publié plus de documents que tout autre mathématicien dans l'histoire, en collaboration avec des centaines de collaborateurs. Les mathématiciens ont un jeu équivalent à la Kevin Bacon jeu, ce qui conduit à l' nombre Erd??s d'un mathématicien. Cela décrit la «distance de collaboration" entre une personne et Paul Erd??s, telle que mesurée par la paternité conjointe de documents mathématiques.
Emmy Noethera été décrit par beaucoup comme la femme la plus importante dans l'histoire des mathématiques, elle a révolutionné les théories de bagues, champs, et alg??bres.
Comme dans la plupart des domaines d'étude, l'explosion des connaissances à l'ère scientifique a conduit à une spécialisation: d'ici la fin du siècle, il y avait des centaines de domaines spécialisés dans les mathématiques et la Classification Mathématique était plusieurs dizaines de pages. De plus en plus de revues mathématiques ont été publiés et, d'ici la fin du siècle, le développement du World Wide Web a conduit à la publication en ligne.
21e si??cle
En 2000, le Clay Mathematics Institute a annoncé les septproblèmes du prix du millénaire, et en 2003, laconjecture de Poincaré a été résolu parGrigori Perelman (qui a refusé d'accepter un prix sur ce point).
La plupart des revues mathématiques ont maintenant des versions en ligne ainsi que les versions imprimées, et de nombreux ligne uniquement revues sont lancés. Il ya un lecteur de plus en plus vers l'édition en libre accès, d'abord popularisée par le arXiv.
Avenir des mathématiques
Il ya beaucoup de tendances observables dans les mathématiques, la plus notable étant que le sujet se développe toujours plus, les ordinateurs sont de plus en plus important et puissant, l'application des mathématiques à la bioinformatique est en pleine expansion, le volume de données à analyser étant produite par la science et la l'industrie, facilitée par les ordinateurs, est explosive en pleine expansion.
