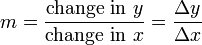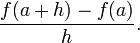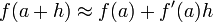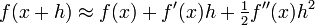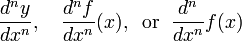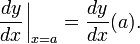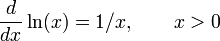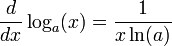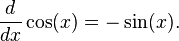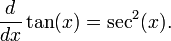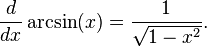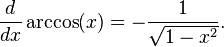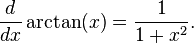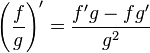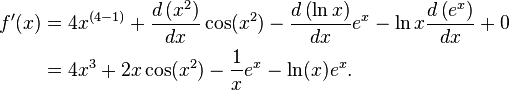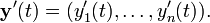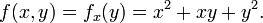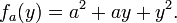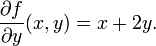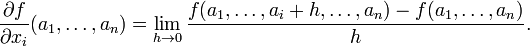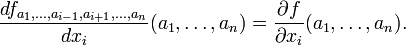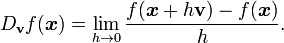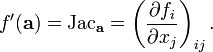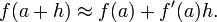D??riv??

Saviez-vous ...

SOS Enfants a essay?? de rendre le contenu plus accessible Wikipedia par cette s??lection des ??coles. Tous les enfants disponibles pour le parrainage de SOS Enfants des enfants sont pris en charge dans une maison de famille pr??s de la charit??. Lire la suite ...

Le graphique d'une fonction, dessin?? en noir, et une tangente ?? cette fonction, dessin??e en rouge. La pente de la tangente est ??gale ?? la d??riv??e de la fonction au point marqu??.

Dans le calcul , une branche de math??matiques , le d??riv?? est une mesure de la fa??on dont une fonction change lorsque les valeurs de ses entr??es changent. Grosso modo, un d??riv?? peut ??tre consid??r?? comme combien une quantit?? est en train de changer ?? un moment donn??. Par exemple, la d??riv??e de la position ou de distance d'un v??hicule ?? un moment donn?? dans le temps est la vitesse instantan??e ou de vitesse instantan??e (respectivement), ?? laquelle la voiture se d??place (l'inverse du int??grale de la vitesse est la position de la voiture).

Une notion ??troitement li??e est le diff??rentielle d'une fonction.

La d??riv??e d'une fonction ?? une valeur d'entr??e choisie d??crit le meilleur approximation lin??aire de la fonction proche de cette valeur d'entr??e. Pour un fonction de valeur r??elle d'une seule variable r??elle, la d??riv??e en un point est ??gal ?? la pente de la tangente ?? la graphe de la fonction ?? ce moment. Dans les dimensions sup??rieures, la d??riv??e d'une fonction en un point est un transformation lin??aire appel??e lin??arisation ..

Le processus de recherche d'un d??riv?? est appel?? diff??renciation. Le th??or??me fondamental du calcul indique que la diff??renciation est le processus inverse ?? l'int??gration .

Diff??renciation et le d??riv??

?? chaque point, le d??riv?? est le une pente de ligne qui est tangente ?? la courbe . La ligne rouge est toujours tangente ?? la courbe bleue; sa pente est le d??riv??.

La diff??renciation est un proc??d?? pour calculer la vitesse ?? laquelle une quantit??, y, les changements par rapport ?? la variation d'une autre quantit??, x, sur lequel il est d??pendante. Ce taux de variation est appel?? la d??riv??e de y par rapport ?? x. En termes plus pr??cis, la d??pendance de y sur x signifie que y est une fonction de x. Si x et y sont des nombres r??els , et si le graphique de y est trac??e contre x, les mesures les d??riv??s pente de ce graphique ?? chaque point. Cette relation fonctionnelle est souvent not??e y = f (x), o?? f repr??sente la fonction.

Le cas le plus simple est lorsque Y est un fonction lin??aire de x, ce qui signifie que le graphe de y contre x est une ligne droite. Dans ce cas, y = f (x) = x m + c, pour les nombres r??els et m c, m et la pente est donn??e par

$m = {\ mbox {} y changer \ over \ mbox {} changer dans x} = {\ Delta y \ over {\ Delta x}}$

o?? le symbole Δ (la forme majuscule de la lettre grecque Delta) est une abr??viation de "changement dans." Cette formule est vrai parce que

Δ y + y = f (x + Δ x) = m (x + Δ x) + c = m x m + c + Δ x = y + x Δ m.

Il en r??sulte que Δ Δ m y = x.

Cela donne une valeur exacte pour la pente d'une ligne droite. Si la fonction f ne est pas lin??aire (ce est ?? dire son graphique ne est pas une ligne droite), cependant, le changement y divis?? par le changement de x varie: la diff??renciation est une m??thode pour trouver une valeur exacte de ce taux de changement ?? tout donn?? La valeur de x.

Figure 1. La tangente ligne ?? (x, f (x))

Figure 2. La s??cante ?? la courbe y = f (x) d??termin??e par des points (x, f (x)) et (x + h, f (x + h)).

Figure 3. La tangente comme limite de s??cantes.

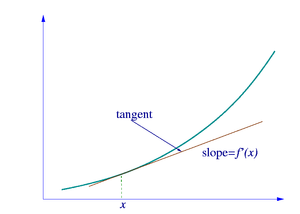
L'id??e, illustr??e par les figures 1 ?? 3, consiste ?? calculer le taux de variation en tant que valeur limite de la rapport des diff??rences Δ Y / Δ x comme Δ x devient infiniment petit.

En Notation de Leibniz, une telle changement infime dans x est not??e dx, et le d??riv?? de y par rapport ?? x est ??crit

$\ Frac {} {dx dy} \, \!$

ce qui sugg??re le rapport de deux quantit??s infinit??simales. (L'expression ci-dessus est prononc?? dans diverses fa??ons telles que "dy dx" ou "dy sur dx". La forme orale "dydx?? est souvent utilis?? de la conversation, m??me si elle peut pr??ter ?? confusion.)

L'approche la plus commune pour transformer cette id??e intuitive dans une d??finition pr??cise utilise limites , mais il ya d'autres m??thodes, telles que analyse non-standard.

D??finition via quotients de diff??rence

Soit y = f (x) une fonction de x. Dans la g??om??trie classique, la tangente ?? un nombre r??el a ??t?? la ligne unique ?? travers le point (a, f (a)), qui ne respectait pas le graphe de f transversalement, ce qui signifie que la ligne ne passe pas directement par le graphique. La d??riv??e de y par rapport ?? x est ?? un, g??om??triquement, la pente de la tangente ?? la courbe de f en un. La pente de la tangente est tr??s proche de la pente de la droite passant par (a, f (a)) et un point sur le graphe ?? proximit??, par exemple (a + h, f (a + h)). Ces lignes sont appel??es droites s??cantes. Une valeur de h proche de z??ro donnera une bonne approximation de la pente de la tangente, et des valeurs plus petites (en valeur absolue ) de h seront, en g??n??ral, donner une meilleure approximations. La pente de la s??cante est la diff??rence entre les valeurs de y de ces points divis?? par la diff??rence entre les valeurs de x, qui est,

$\ Frac {f (a + h) -f (a)} {} h.$

Cette expression est Newton s ' diff??rence quotient. Le d??riv?? est la valeur du quotient de la diff??rence que les lignes s??cantes se rapprocher et plus proche de la ligne tangente. Formellement, la d??riv??e de la fonction f ?? un est la limite

$f '(a) = \ lim_ {h \ 0} {f (a + h) -f (a) \ over h}$

du quotient de diff??rence en tant h tend vers z??ro, si cette limite existe. Si la limite existe, alors f est diff??rentiable en a. Voici (a) est une f de plusieurs notations communes pour le d??riv?? ( voir ci-dessous ).

??quivalente, le d??riv?? satisfait la propri??t?? que

$\ Lim_ {h \ 0} {f (a + h) -f (a) - f '(a) \ cdot h \ over h} = 0,$

qui a l'interpr??tation intuitive (voir Figure 1) que la tangente ?? f ?? une donne le meilleur approximation lin??aire

$f (a + h) \ env f (a) + f '(a) h$

?? f pr??s d'un (ce est ?? dire, pour les petits h). Cette interpr??tation est le plus facile de g??n??raliser ?? d'autres param??tres ( voir ci-dessous ).

La substitution de 0 ?? h dans les causes diff??rence de quotient la division par z??ro, de sorte que la pente de la tangente ne se trouvent pas directement. Au lieu de cela, d??finissent Q (h) comme ??tant le quotient de la diff??rence en fonction de h:

$Q (h) = \ frac {f (a + h) - f (a)} {h}$ .

Q (h) est la pente de la droite s??cante entre (a, f (a)) et (a + h, f (a + h)). Si f est une fonction continue, ce qui signifie que son graphe est une courbe continue sans ??carts, alors Q est une fonction continue loin du point h = 0. Si la limite 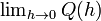$\ Textstyle \ lim_ {h \ 0} Q (h)$ existe, ce qui signifie qu'il ya une fa??on de choisir une valeur pour Q (0) ce qui rend le graphique de Q une fonction continue, alors la fonction f est diff??rentiable au point a, et son d??riv?? ?? une ??gale Q (0).

Dans la pratique, la continuit?? de la diff??rence quotient Q (h) ?? h = 0 est repr??sent??e en modifiant le num??rateur pour annuler h dans le d??nominateur. Ce processus peut ??tre long et fastidieux pour les fonctions complexes, et de nombreux raccourcis sont couramment utilis??s pour simplifier le processus.

Exemple

La fonction d'??l??vation au carr?? f (x) = x ?? est diff??rentiable en x = 3, et son d??riv?? est l?? 6. Ceci est prouv?? par l'??criture du quotient de diff??rence comme suit:

${F (3 + h) -f (3) \ over h} = {(3 + h) ^ 2-9 \ over {h}} = {9 + 6h + h ^ 2-9 \ over {h}} = {6h + h ^ 2 \ over {h}} = 6 + h.$

Alors nous obtenons la fonction simplifi??e dans la limite:

$\ Lim_ {h \ 0} 6 h = + 6 + 0 = 6.$

La derni??re expression montre que le quotient de diff??rence est ??gale ?? 6 + h lorsque h ne est pas z??ro et ne est pas d??finie lorsque h est ??gal ?? z??ro. (Rappelez-vous qu'en raison de la d??finition du quotient de diff??rence, le quotient de diff??rence est toujours pas d??finie lorsque h est z??ro.) Cependant, il est un moyen naturel de remplir une valeur pour le quotient de diff??rence ?? z??ro, ?? savoir 6. D'o?? la pente de la courbe de la fonction d'??l??vation au carr?? au point (3, 9) est de 6, et ainsi de son d??riv?? ?? x = 3 est f '(3) = 6.

Plus g??n??ralement, un calcul similaire montre que la d??riv??e de la fonction d'??l??vation au carr?? ?? x = est un f '(a) = 2 a.

Continuit?? et d??rivabilit??

Cette fonction ne est pas un d??riv?? au point marqu??, que la fonction ne est pas continue l??.

Si y = f (x) est d??rivable en a, alors f doit ??galement ??tre continue ?? une. Par exemple, choisir un point A et soit f la fonction de l'??tape qui retourne une valeur, soit 1, pour tout x moins d'un, et retourne une valeur diff??rente, disons 10, pour tout x sup??rieur ou ??gal ?? un. f ne peut pas avoir un d??riv?? ?? un. Si h est n??gatif, alors a + h est sur la partie basse de l'??tape, de sorte que la ligne ?? partir d'une s??cante ?? une H + sera tr??s raide, et lorsque h tend vers z??ro, la pente tend vers l'infini. Si h est positif, alors a + h est sur la partie haute de l'??tape, de sorte que la s??cante d'un ?? un H + aura pente nulle. En cons??quence, les droites s??cantes ne se approchent pas de pente unique, donc ne existe pas la limite du quotient de diff??rence.

La fonction valeur absolue est continue, mais ne parvient pas ?? ??tre diff??rentiable en x = 0 car il a un angle vif.

Cependant, m??me si une fonction est continue en un point, il peut ne pas ??tre diff??rentiables il. Par exemple, la valeur absolue fonction y = | x | est continue en x = 0, mais il ne est pas diff??rentiable il. Si h est positif, alors la pente de la droite s??cante de 0 ?? h est un, alors que si h est n??gative, alors la pente de la droite s??cante de 0 ?? h est n??gatif. Ceci peut ??tre vu graphiquement comme un ??coude?? dans le graphique ?? x = 0. M??me une fonction avec un graphique en douceur ne est pas diff??rentiable en un point o?? sa tangente est verticale: Par exemple, la fonction y = ³ √ x ne est pas diff??rentiable en x = 0.

La plupart des fonctions qui se produisent dans la pratique ont d??riv??s ?? tous les points ou ?? presque tous les points. Cependant, ?? la suite de Stefan Banach stipule que l'ensemble des fonctions qui ont un d??riv?? ?? un moment donn?? est une ensemble maigre en l'espace de toutes les fonctions continues. Officieusement, cela signifie que les fonctions diff??rentiables sont tr??s atypique parmi les fonctions continues. Le premier exemple connu d'une fonction qui est continue partout mais nulle part diff??rentiable est le Fonction de Weierstrass.

Le d??riv?? en fonction

Soit f une fonction qui a une d??riv??e en tout point un dans le domaine de f. Parce que chaque point a une d??riv??e, il est une fonction qui envoie le point A ?? la d??riv??e de f ?? un. Cette fonction se ??crit f '(x) et est appel?? la fonction d??riv??e ou la d??riv??e de f. La d??riv??e de f rassemble tous les d??riv??s de f ?? tous les points dans le domaine de f.

Parfois f a une d??riv??e au plus, mais pas tous, les points de son domaine. La fonction dont la valeur est ??gale ?? une f '(a) si f' (a) est d??fini et ne est pas d??fini ailleurs est ??galement appel?? la d??riv??e de f. Il est encore une fonction, mais son domaine est strictement inf??rieure ?? la domaine de f.

En utilisant cette id??e, la diff??renciation devient une fonction de fonctions: Le d??riv?? est un l'op??rateur dont le domaine est l'ensemble de toutes les fonctions qui ont d??riv??s en tout point de leur domaine et dont la gamme est un ensemble de fonctions. Si l'on d??signe par cet op??rateur D, puis D (f) est la fonction f '(x). Depuis D (f) est une fonction, il peut ??tre ??valu?? ?? un point a. D'apr??s la d??finition de la fonction d??riv??e, D (f) (a) = f '(a).

A titre de comparaison, consid??rer la fonction de doublement f (x) = x 2; f est une fonction ?? valeur r??elle d'un nombre r??el, ce qui signifie qu'il prend num??ros comme entr??es et sorties a nombres comme:

$\ Begin {align} 1 & {} \ mapsto 2, 2 \\ & {} \ mapsto 4, 3 \\ & {} \ mapsto 6. \ end {align}$

L'op??rateur D, cependant, ne est pas d??fini sur un num??ro individuel. Il est d??fini que sur les fonctions:

$\ Begin {align} D (x \ mapsto 1) & = (x \ mapsto 0), \\ D (x \ mapsto x) & = (x \ mapsto 1), \\ D (x \ mapsto x ^ 2) & = (x \ mapsto 2 \ cdot x). \ End {align}$

Parce que la sortie de D est une fonction dont la sortie D peut ??tre ??valu?? ?? un point. Par exemple, lorsque D est appliqu??e ?? la fonction de mise au carr??,

$x \ mapsto x ^ 2,$

D envoie la fonction de doublement,

$x \ mapsto 2x,$

que nous avons nomm??e f (x). Cette fonction de sortie peut alors ??tre ??valu??e pour obtenir f (1) = 2, f (2) = 4, et ainsi de suite.

D??riv??s plus ??lev??s

Soit f une fonction d??rivable, et f '(x) son d??riv??. La d??riv??e de f '' (x) (se il en a un) est ??crit f '(x) et est appel?? la d??riv??e seconde de f. De m??me, la d??riv??e d'une d??riv??e seconde, si elle existe, se ??crit f '' '(x) et est appel?? le troisi??me d??riv??e de f. Ces d??riv??s r??p??t??es sont appel??s d??riv??s d'ordre sup??rieur.

Une fonction f peut ??tre d??pourvu d'un d??riv??, par exemple, si elle ne est pas continue. De m??me, m??me si f a un d??riv??, il peut ne pas avoir une d??riv??e seconde. Par exemple, laissez-

$f (x) = \ begin {} cas x ^ 2, et \ mbox {if} x \ ge 0 \\ -x ^ 2, et \ mbox {if} x \ le 0 \ end {} cas$ .

Un calcul ??l??mentaire montre que f est une fonction dont la d??riv??e est diff??rentiable

$f '(x) = \ begin {} cas 2x, et \ mbox {if} x \ ge 0 \\ -2x, & \ mbox {if} x \ le 0 \ end {} cas$ .

f '(x) est le double de la fonction valeur absolue, et il n'a pas un d??riv?? ?? z??ro. Des exemples similaires montrer qu'une fonction peut avoir des d??riv??s de k pour tout entier k non-n??gatif, mais pas (k + 1) d??riv?? -order. Une fonction qui a des d??riv??es successives k est appel?? k fois d??rivable. Si en plus la k i??me d??riv??e est continue, alors la fonction est dit ??tre des diff??rentiabilit?? classe C ^k. (Ce est une condition plus forte que d'avoir des d??riv??s de k. Pour un exemple, voir classe diff??rentiabilit??.) Une fonction qui a une infinit?? de d??riv??s est appel?? ind??finiment diff??rentiable ou lisse.

Sur la ligne r??elle, chaque fonction polynomiale est infiniment diff??rentiable. Par la norme r??gles de diff??renciation, si un polyn??me de degr?? n est diff??renci?? n fois, alors il devient un fonction constante. Tous ses d??riv??s ult??rieures sont identiquement nulle. En particulier, ils existent, afin polyn??mes sont des fonctions lisses.

Les d??riv??s d'une fonction f ?? un point x fournissent des approximations polyn??mes ?? cette fonction ?? proximit?? de x. Par exemple, si f est deux fois d??rivable, puis

$f (x + h) \ env f (x) + f '(x) + h \ tfrac12 f' '(x) h ^ 2$

en ce sens que

$\ Lim_ {h \ 0} \ frac {f (x + h) - f (x) - f '(x) h - \ frac12 f' '(x) h ^ 2} {h ^ 2} = 0.$

Si f est infiniment diff??rentiable, alors ce est le d??but de la s??rie de Taylor pour f.

Notations de diff??renciation

Notation de Leibniz

La notation pour les produits d??riv??s introduits par Gottfried Leibniz est l'un des premiers. Il est encore couramment utilis??e lorsque l'??quation y = f (x) est consid??r??e comme une relation fonctionnelle entre variables d??pendantes et ind??pendantes. Ensuite, le premier d??riv?? est d??sign?? par

$\ Frac {} {dy dx}, \ quad \ frac {} {df dx} (x), \; \; \ mathrm {ou} \; \; \ Frac {d} {dx} f (x).$

D??riv??s plus ??lev??s sont exprim??s en utilisant la notation

$\ Frac {d ^ ny} {dx ^ n}, \ quad \ frac {d ^ nf} {dx ^ n} (x), \; \; \ mathrm {ou} \; \; \ Frac {d ^ n} {dx ^ n} f (x)$

pour la n i??me d??riv??e de y = f (x) (par rapport ?? x).

Avec la notation de Leibniz, nous pouvons ??crire la d??riv??e de y au point x = une de deux fa??ons diff??rentes:

$\ Frac {} {dx dy} \ left {\ \ \ frac {} {}!} \ Right |. _ {X = a} = \ frac {} {dx dy} (a).$

Notation de Leibniz permet de sp??cifier la variable de diff??renciation (dans le d??nominateur). Ceci est particuli??rement pertinent pour les diff??rentiation partielle. Il rend ??galement le r??gle facile ?? retenir de la cha??ne:

$\ Frac {} {dx dy} = \ frac {} {dy du} \ cdot \ frac {du} {dx}.$

La notation de Lagrange

Un des notations modernes les plus courantes pour la diff??renciation est due ?? Joseph Louis Lagrange et utilise le Premier marque, f sorte que la d??riv??e d'une fonction f (x) est not??e '(x) ou tout simplement f'. De m??me, les seconde et troisi??me d??riv??s sont d??sign??s

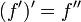$(F ')' = f '' \,$ et $(F '') '= f' '' \ ,.$

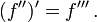
Au-del?? de ce point, certains auteurs utilisent chiffres romains tels que

$f ^ {\ mathrm {iv}} \,$

pour le quatri??me d??riv??, alors que d'autres auteurs placent au nombre de d??riv??s entre parenth??ses:

$f ^ {(4)} \,$

Cette derni??re notation g??n??ralise pour donner le f notation ⁽ⁿ⁾ pour le n-i??me d??riv??e de f - cette notation est tr??s utile lorsque l'on veut parler de la d??riv??e comme ??tant une fonction elle-m??me, comme dans ce cas la notation Leibniz peut devenir encombrant.

La notation de Newton

La notation de Newton pour la diff??renciation, aussi appel??e la notation par points, met un point sur le nom de la fonction de repr??senter un d??riv??. Si y = f (t), et

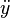
$\ Dot {y}$ et $\ Ddot {y}$

d??signent, respectivement, les premi??re et deuxi??me d??riv??es de y par rapport ?? t. Cette notation est utilis??e presque exclusivement pour d??riv??es dans le temps, ce qui signifie que la variable ind??pendante de la fonction repr??sente le temps . Il est tr??s commun dans la physique et dans les disciplines math??matiques li??s ?? la physique telles que les ??quations diff??rentielles . Alors que la notation devient ing??rable pour les d??riv??s d'ordre ??lev??, dans la pratique, que tr??s peu de d??riv??s sont n??cessaires.

La notation d'Euler

Euler notation s 'utilise une op??rateur diff??rentiel D, qui est appliqu?? ?? une fonction f pour donner le d??riv?? premier Df. La d??riv??e seconde est not??e D ² f, et la n i??me d??riv?? est d??sign?? D ⁿ f.

Si y = f (x) est une variable d??pendante, alors souvent l'indice x est fix?? ?? la D pour clarifier la variable ind??pendante x. La notation d'Euler se ??crit alors

$D_x y \,$ ou $D_x f (x) \,$ ,

bien que cela indice est souvent omis lorsque la variable x est compris, par exemple, lorsque ce est la seule pr??sente variable dans l'expression.

La notation d'Euler est utile pour ??noncer et r??soudre ??quations diff??rentielles lin??aires.

Le calcul de la d??riv??e

La d??riv??e d'une fonction peut, en principe, ??tre calcul??e ?? partir de la d??finition en consid??rant le quotient de la diff??rence et le calcul de la limite. Pour quelques exemples, voir D??riv??s (exemples). Dans la pratique, une fois que les d??riv??s de quelques fonctions simples sont connus, les d??riv??s d'autres fonctions sont plus facilement calcul??es en utilisant les r??gles d'obtention de d??riv??s de fonctions plus complexes ?? partir de plus simples.

D??riv??s de fonctions ??l??mentaires

En outre, les d??riv??s de certaines fonctions communes sont utiles ?? conna??tre.

D??riv??s de pouvoirs: si

$f (x) = x ^ r \,$ ,

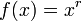o?? r est tout nombre r??el , alors

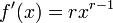$f '(x) = rx ^ {r-1} \,$ ,

o?? cette fonction est d??finie. Par exemple, si r = 1/2, puis

$f '(x) = \ frac {1} {2} x ^ {- \ tfrac12} \,$ .

et la fonction est d??finie que pour x non-n??gative. Lorsque r = 0, cette r??gle r??cup??re la r??gle constante.

Exponentielles et logarithmes fonctions:

$\ Frac {d} {dx} e ^ x = e ^ x$

$\ Frac {d} {} dx = a ^ x \ ln (a) a ^ x$

$\ Frac {d} {dx} \ ln (x) = 1 / x, \ qquad x> 0$

$\ Frac {d} {dx} \ log_a (x) = \ frac {1} {x \ ln (a)}$

Les fonctions trigonom??triques :

$\ Frac {d} {dx} \ sin (x) = \ cos (x).$

$\ Frac {d} {dx} \ cos (x) = - \ sin (x).$

$\ Frac {d} {dx} \ tan (x) = \ s ^ 2 (x).$

Fonctions trigonom??triques inverses:

$\ Frac {d} {dx} \ arcsin (x) = \ frac {1} {\ sqrt {1-x ^ 2}}.$

$\ Frac {d} {dx} \ arccos (x) = - \ frac {1} {\ sqrt {1-x ^ 2}}.$

$\ Frac {d} {dx} \ arctan (x) = \ frac {1} {{1 + x ^ 2}}.$

R??gles pour trouver le d??riv??

Dans de nombreux cas, les calculs compliqu??s de limites par l'application directe de la diff??rence le quotient de Newton peuvent ??tre ??vit??s en utilisant les r??gles de diff??renciation. Certaines des r??gles les plus ??l??mentaires sont les suivants.

R??gle constante: si f (x) est constante, alors

$f '= 0 \,$

R??gle Somme:

$(Af + bg) '= af' + bg \ ',$ pour toutes les fonctions F et G et tous les nombres r??els a et b.

r??gle de produit:

$(Fg) '= f' g + fg \ ',$ pour toutes les fonctions f et g.

Quotient r??gle:

$\ Left (\ frac {f} {g} \ right) '= \ frac {f'g - fg'} {g ^ 2}$

r??gle de la cha??ne: Si 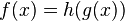$f (x) = h (g (x))$ , Puis

$f '(x) = h' (g (x)) g '(x) \,$ .

Exemple de calcul

Le d??riv?? de

$f (x) = x ^ 4 + \ sin (x ^ 2) - \ ln (x) e ^ x + 7 \,$

est

$\ Begin {align} f '(x) = & 4 x ^ {(4-1)} + \ frac {d \ gauche (x ^ 2 \ right)} {dx} \ cos (x ^ 2) - \ frac {d \ gauche (\ ln {x} \ right)} {dx} e ^ x - \ ln {x} \ frac {d \ gauche (e ^ x \ right)} {dx} + 0 = \\ & 4x ^ 3 + 2x \ cos (x ^ 2) - \ ln (x) e ^ x - de frac {1} {x} e ^ x \. \ End {align}$

Voici le second terme a ??t?? calcul?? en utilisant la r??gle de la cha??ne et la troisi??me en utilisant la r??gle du produit: les d??riv??s connus des fonctions ??l??mentaires x ??, x ^4, sin (x), ln (x) et exp (x) = e ^x ont ??galement ??t?? utilis??s .

D??riv??s de dimensions sup??rieures

D??riv??s de fonctions vectorielles valeur

Un valeurs vectorielles fonction y (t) d'une variable r??elle est une fonction qui envoie des nombres r??els ?? des vecteurs dans certains espace vectoriel R ^n. Une fonction de vecteur ?? valeur peut ??tre subdivis??e en ses fonctions de coordonn??es y ₁ (t), y ₂ (t), ..., y _n (t), ce qui signifie que y (t) = (y ₁ (t), ... , y _n (t)). Cela comprend, par exemple, courbes param??triques par R ² ou R ^3. Les fonctions coordonn??es sont r??elles fonctions ??valu??es, de sorte que la d??finition ci-dessus de d??riv?? se applique ?? eux. La d??riv??e de y (t) est d??fini comme ??tant le vecteur , appel?? le vecteur tangent, dont les coordonn??es sont les d??riv??es des fonctions de coordonn??es. C'est,

$\ Mathbf {y} '(t) = (y'_1 (t), \ ldots, y'_n (t)).$

De mani??re ??quivalente,

$\ Mathbf {y} '(t) = \ lim_ {h \ 0} \ frac {\ mathbf {y} (t + h) - \ mathbf {y} (t)} {h},$

si la limite existe. La soustraction dans le num??rateur est la soustraction de vecteurs, et non scalaires. Si la d??riv??e de y existe pour chaque valeur de t, alors y 'est une autre fonction de valeurs vectorielles.

Si e _1, ..., e _n est la norme de base pour R ^n, y (t) peut aussi se ??crire comme y ₁ (t) e ₁ + ... + y _n (t) e _n. Si nous supposons que la d??riv??e d'une fonction vectorielle ??valu??s conservent la propri??t?? de lin??arit??, la d??riv??e de y (t) doit ??tre

$y'_1 (t) \ mathbf {e} _1 + \ cdots + y'_n (t) \ mathbf {e} _n$

parce que chacun des vecteurs de base est une constante.

Cette g??n??ralisation est utile, par exemple, si y (t) est le vecteur de position d'une particule ?? l'instant t; alors le d??riv?? de y '(t) est la vitesse de la particule vecteur ?? l'instant t.

D??riv??es partielles

Supposons que f est une fonction qui d??pend de plus d'une variable. Par exemple,

$f (x, y) = x ^ 2 + xy + y ^ 2. \,$

f peut ??tre r??interpr??t?? comme une famille de fonctions d'une variable index?? par les autres variables:

$f (x, y) = f_x (y) = x ^ 2 + xy + y ^ 2. \,$

En d'autres termes, ?? chaque valeur de x choisit une fonction not??e f _x, qui est une fonction d'un nombre r??el. C'est,

$x \ mapsto f_x, \,$

$f_x (y) = x ^ 2 + xy + y ^ 2. \,$

Une fois qu'une valeur de x est choisi, par exemple un, alors f (x, y) d??termine une fonction f qui y envoie _un ?? un ?? + ay + y ??:

$f_a (y) = a ^ ay + 2 + y ^ 2. \,$

Dans cette expression, a est un, pas une variable constante, de sorte que f _a est _une fonction d'une seule variable r??elle. Par cons??quent, la d??finition de la d??riv??e d'une fonction d'une variable se applique:

$f_a '(y) = a + 2y. \,$

La proc??dure ci-dessus peut ??tre r??alis??e pour ne importe quel choix d'un. Assemblage des d??riv??s, ainsi que dans une fonction donne une fonction qui d??crit la variation de f dans la direction y:

$\ Frac {\ part f} {\ part y} (x, y) = x + 2y.$

Ce est la d??riv??e partielle de f par rapport ?? y. Voici ∂ est une d arrondi appel?? le symbole d??riv??e partielle. Pour le distinguer de la lettre d, ∂ est parfois prononc?? "der", "del", ou "partielle" au lieu de "dee".

En g??n??ral, la d??riv??e partielle d'une fonction f (x _1, ..., x _n) dans la direction x _i au point (a ₁ ..., a _n) est d??fini comme ??tant:

$\ Frac {\ part f} {\ part x_i} (a_1, \ ldots, a_n) = \ lim_ {h \ 0} \ frac {f (a_1, \ ldots, a_i + h, \ ldots, A_N) - f (a_1, \ ldots, a_n)} {} h.$

Dans la diff??rence quotient ci-dessus, toutes les variables, sauf x _i sont maintenus fixes. Ce choix de valeurs fixes d??termine une fonction d'une variable

$F_ {a_1, \ ldots, a_ {i-1}, {a_ i + 1}, \ ldots, a_n} (x_i) = f (A_1, \ ldots, a_ {i-1}, x_i, a_ {i + 1}, \ ldots, a_n)$

et, par d??finition,

$\ Frac {{df_ A_1, \ ldots, a_ {i-1}, {a_ i + 1}, \ ldots, a_n}} {} dx_i (a_1, \ ldots, a_n) = \ frac {\ part f} { \ part x_i} (a_1, \ ldots, A_N).$

En d'autres termes, les diff??rents choix d'un indice d'une famille de fonctions ?? une variable de m??me que dans l'exemple ci-dessus. Cette expression montre ??galement que le calcul des d??riv??es partielles r??duit pour le calcul des d??riv??s ?? une variable.

Un exemple important d'une fonction de plusieurs variables est le cas d'un fonction f de scalaires (x _1, ... x _n) sur un domaine dans l'espace euclidien R ⁿ (par exemple, le R ou R ?? ??). Dans ce cas f a une d??riv??e partielle ∂ f / ∂ _{x j} par rapport ?? chaque variable x _j. Au point a, ces d??riv??es partielles d??finissent le vecteur

$\ Nabla f (a) = \ left (\ frac {\ f partielle} {\ x_1 partielle} (a), \ ldots, \ frac {\ f partielle} {\ de x_n partielle} (a) \ right).$

Ce vecteur est appel?? le gradient de f en un. Si f est d??rivable en tout point dans certains domaine, le gradient est une fonction ∇ vecteur f-valeur qui prend le point a au vecteur ∇ f (a). En cons??quence, le gradient d??termine une champ de vecteurs.

D??riv??es directionnelles

Si f est une fonction ?? valeurs r??elles sur R ^n, alors les d??riv??es partielles de f mesure la variation dans la direction des axes de coordonn??es. Par exemple, si f est une fonction de x et y, puis ses d??riv??es partielles mesurent la variation de f dans la direction x et la direction y. Ils ne ont pas, cependant, de mesurer directement la variation de f dans une autre direction, comme le long de la ligne y diagonales = x. Ils sont ??valu??s en utilisant des d??riv??s directionnelles. Choisissez un vecteur

$\ Mathbf {v} = (v_1, \ ldots, V_n).$

La d??riv??e directionnelle de f dans la direction de v au point x est la limite

$D _ {\ mathbf {v}} {f} (\ boldsymbol {x}) = \ lim_ {h \ rightarrow 0} {\ frac {f (\ boldsymbol {x} + h \ mathbf {v}) - f (\ boldsymbol {x})} {h}}.$

Soit λ ??tre un scalaire. La substitution de h / λ pour h change diff??rence le quotient de λ v direction dans les temps λ diff??rence de quotient de la direction de v. Par cons??quent, la d??riv??e directionnelle dans la direction de λ c λ est la fois d??riv??e directionnelle dans la direction de v. Pour cette raison, d??riv??es directionnelles sont souvent consid??r??s uniquement pour les vecteurs unitaires c.

Si toutes les d??riv??es partielles de f existent et sont continues en x, puis ils d??terminent la d??riv??e directionnelle de f dans la direction v par la formule:

$D _ {\ mathbf {v}} {f} (\ boldsymbol {x}) = \ sum_ {j = 1} ^ n v_j \ frac {\ f partielle} {\ x_j partielle}.$

Ceci est une cons??quence de la d??finition de la d??riv??e totale. Il se ensuit que la d??riv??e directionnelle est lin??aire dans v.

La m??me d??finition fonctionne ??galement lorsque f est une fonction ?? valeurs dans R ^m. On utilise simplement la d??finition ci-dessus dans chacune des composantes des vecteurs. Dans ce cas, la d??riv??e directionnelle est un vecteur de R ^m.

La d??riv??e totale, l'??cart total et le jacobien

Soit f une fonction ?? partir d'un domaine dans R ?? R. La d??riv??e de f en un point a dans son domaine est la meilleure approximation lin??aire ?? f ?? ce point. Comme ci-dessus, ce est un nombre. G??om??triquement, si v est un vecteur d'unit?? en commen??ant ?? un, alors f '(a), la meilleure approximation lin??aire de f en a, doit ??tre la longueur du vecteur v trouv?? en d??pla??ant vers l'espace cible ?? l'aide f. (Ce vecteur est appel?? pushforward de v par f et est habituellement ??crite 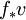$f_ * v$ .) En d'autres termes, si v est mesur??e en termes de distances sur la cible, alors, parce que v ne peut ??tre mesur??e par f, v ne semble plus ??tre un vecteur de l'unit?? parce f ne pr??serve pas des vecteurs unitaires. Au lieu de cela semble avoir v longueur f '(a). Si m est sup??rieur ?? un, puis en ??crivant f en utilisant des fonctions de coordonn??es, la longueur de v dans chacune des directions de coordonn??es peut ??tre mesur??e s??par??ment.

Supposons maintenant que f est une fonction d'un domaine ?? R ⁿ ?? ^m et que R a est un point dans le domaine de f. La d??riv??e de f ?? une devrait toujours ??tre la meilleure approximation lin??aire pour f ?? un. En d'autres termes, si v est un vecteur de R ^n, f '(a) doit ??tre le transformation lin??aire qui approxime le mieux f. La transformation lin??aire doit contenir toutes les informations sur la fa??on f transforme vecteurs ?? un des vecteurs ?? f (a), et en symboles, ce qui signifie qu'il devrait ??tre la transformation lin??aire f '(a) de telle sorte que

$\ {Lim_ || \ mathbf {h} || \ rightarrow 0} \ frac {|| f (\ mathbf {a} + \ mathbf {h}) - f (\ mathbf {a}) - f '(\ mathbf {a}) \ mathbf {h}} {|| || \ mathbf {h}} || = 0.$

Voici h est un vecteur de R ^n, de sorte que le norme dans le d??nominateur est la longueur standard sur R ^n. Cependant, f '(a) h est un vecteur de R ^m, et la norme dans le num??rateur est la longueur standard sur R ^m. La transformation lin??aire f '(a), se il existe, est appel??e la d??riv??e totale de f ?? un ou le (s) diff??rentielle de f en a.

Si la d??riv??e totale existe ?? un, tous les d??riv??es partielles de f existent ?? un. Si l'on ??crit f en utilisant des fonctions de coordonn??es, de sorte que f = (f _1, f _2, ..., f _m), la d??riv??e totale peut ??tre exprim?? comme une matrice appel??e Matrice jacobienne de f en un:

$f '(\ mathbf {a}) = \ text {} Jac _ {\ mathbf {a}} = \ left (\ frac {\ f_i partielle} {\ x_j partielle} \ right) _ {} ij.$

L'existence de la jacobienne est strictement plus forte que l'existence de toutes les d??riv??es partielles, mais si les d??riv??es partielles existent et satisfont ?? des conditions de r??gularit?? doux, alors la d??riv??e totale existe et est donn?? par la jacobienne.

La d??finition de la d??riv??e totale englobe la d??finition de la d??riv??e dans une variable. Dans ce cas, le d??riv?? totale existe si et seulement si le d??riv?? d'habitude existe. La matrice jacobienne est r??duite ?? une matrice 1 ?? 1 dont l'entr??e est uniquement la d??riv??e f '(x). Cette matrice 1 ?? 1 satisfait la propri??t?? que f (a + h) - f (a) - f '(a) h est approximativement nulle, en d'autres termes que

$f (a + h) \ env f (a) + f '(a) h.$

Jusqu'?? des variables changeantes, ce est la d??claration que la fonction 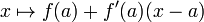$x \ mapsto f (a) + f '(a) (x-a)$ est la meilleure approximation lin??aire de f ?? un.

Le d??riv?? d'une fonction totale ne donne pas une autre fonction de la m??me fa??on que des cas une variable. Ce est parce que la d??riv??e totale d'une fonction multivari??e doit enregistrer beaucoup plus d'informations que la d??riv??e d'une fonction ?? une seule variable. Au lieu de cela, le d??riv?? totale donne une fonction de la faisceau tangent ?? la source de faisceau de la tangente de la cible.

G??n??ralisations

Le concept d'un d??riv?? peut ??tre ??tendu ?? bien d'autres param??tres. Le d??nominateur commun est que la d??riv??e d'une fonction en un point sert de approximation lin??aire de la fonction ?? ce moment.

Une g??n??ralisation des pr??occupations importantes d??riv??s complexes des fonctions de variables complexes, telles que les fonctions de (dans un domaine) le nombres complexes C ?? C. La notion de la d??riv??e d'une telle fonction est obtenue en rempla??ant les variables r??elles avec des variables complexes dans la d??finition. Cependant, cette d??finition innocente se cache des propri??t??s tr??s profondes. Si C est identifi?? avec R ?? en attribuant un nombre complexe z comme x + y i, puis une fonction diff??rentiable de C ?? C est certainement diff??rentiable en fonction de R ?? R ?? ?? (en ce sens que ses d??riv??es partielles existent tous) , mais l'inverse ne est pas vrai en g??n??ral: le d??riv?? complexe ne existe que si le d??riv?? r??el est lin??aire complexe et cela impose des relations entre les d??riv??es partielles appel?? ??quations de Cauchy Riemann - voir fonctions holomorphes.

Un autre concerne la g??n??ralisation fonctions entre vari??t??s diff??rentiables ou lisses. Intuitivement parle une telle vari??t?? M est un espace qui peut ??tre approch??e ?? proximit?? de chaque point x par un espace vectoriel appel?? son espace tangente: l'exemple prototypique est un surface lisse en R ??. Le d??riv?? (ou diff??rentiel) d'un (diff??rentiables) f: M → N entre les collecteurs, ?? un point x dans M, est alors une lin??aire de l'espace tangent de M en x ?? l'espace tangent de N ?? f (x). La fonction d??riv??e devient une carte entre le tangents faisceaux de m et n. Cette d??finition est fondamentale dans la g??om??trie diff??rentielle et a de nombreuses utilisations - voir pushforward (diff??rentiel) et recul (g??om??trie diff??rentielle).

Diff??renciation peut ??galement ??tre d??finie pour les cartes entre dimension infinie espaces vectoriels tels que Espaces de Banach et Espaces de Fr??chet. Il est ?? la fois une g??n??ralisation de la d??riv??e directionnelle, appel??e G??teaux d??riv??, et de l'??cart, appel?? le Fr??chet.

Un d??ficit du d??riv?? classique est que pas beaucoup de fonctions sont diff??rentiables. N??anmoins, il existe un moyen d'??tendre la notion de la d??riv??e de sorte que toutes des fonctions continues et de nombreuses autres fonctions peuvent ??tre diff??renci??es en utilisant un concept connu sous le nom d??riv??e faible. L'id??e est d'int??grer les fonctions continues dans un espace plus large appel?? l'espace de distributions et ne n??cessitent qu'une fonction est diff??rentiable "en moyenne".

Les propri??t??s du d??riv?? ont inspir?? l'introduction et l'??tude de nombreux objets similaires en alg??bre et topologie - voir, par exemple, alg??bre diff??rentielle.

R??cup??r?? ?? partir de " http://en.wikipedia.org/w/index.php?title=Derivative&oldid=198886698"