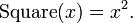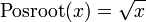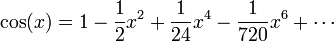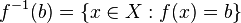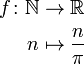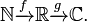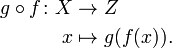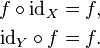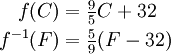Fonction (math??matiques)

Graphique de l'exemple de fonction,

La math??matique notion de fonction exprime la d??pendance entre deux grandeurs, dont l'une est indiqu??e (le variable ind??pendante, argument de la fonction, ou de son "entr??e") et l'autre produit (la variable d??pendante, la valeur de la fonction, ou "sortie"). Une fonction associe une seule sortie pour chaque ??l??ment d'entr??e partant d'un fixe d??finir, tels que les nombres r??els .

Il ya plusieurs fa??ons de donner une fonction: par une formule , par une intrigue ou graphique, par un algorithme qui calcule ce, d'une description de ses propri??t??s. Parfois, une fonction est d??crite ?? travers sa relation ?? d'autres fonctions (voir, par exemple, la fonction inverse ). Dans les disciplines appliqu??es, les fonctions sont souvent sp??cifi??es par leurs tableaux de valeurs ou par une formule. Pas tous les types de la description peuvent ??tre donn??s pour chaque fonction possible, et il faut faire une distinction nette entre la fonction elle-m??me et plusieurs fa??ons de pr??senter ou de le visualiser.

Une id??e de grande importance dans l'ensemble des math??matiques est la composition de fonctions : si z est une fonction de y et y est une fonction de x, alors z est une fonction de x. On peut d??crire de fa??on informelle en disant que la fonction composite est obtenu en utilisant la sortie de la premi??re fonction en tant que l'entr??e de la seconde. Cette fonctionnalit?? des fonctions les distingue des autres constructions math??matiques, comme les num??ros ou chiffres, et fournit la th??orie des fonctions avec sa structure la plus puissante.

Introduction

Fonctions jouent un r??le fondamental dans tous les domaines des math??matiques, ainsi que dans les autres sciences et de l'ing??nierie. Cependant, l'intuition se rapportant ?? des fonctions, la notation, et m??me le sens m??me du terme ??fonction?? varie entre les champs. Plus de zones abstraites des math??matiques, comme la th??orie des ensembles , consid??rent types tr??s g??n??raux de fonctions, qui ne peuvent ??tre sp??cifi??es par une r??gle concr??te et ne sont pas r??gis par des principes familiers. La propri??t?? caract??ristique d'une fonction dans le sens le plus abstrait est qu'elle concerne pr??cis??ment une sortie ?? chacune de ses entr??es admissibles. Ces fonctions ne implique pas n??cessairement le nombre et peuvent, par exemple, associer chacun d'un ensemble de mots avec leurs propres premi??res lettres.

Fonctions dans l'alg??bre sont g??n??ralement exprimable en termes de op??rations alg??briques. Fonctions ??tudi??s dans l'analyse , comme la fonction exponentielle , peuvent avoir des propri??t??s suppl??mentaires r??sultant de la continuit?? de l'espace, mais dans le cas le plus g??n??ral ne peuvent pas ??tre d??fini par une formule unique. Fonctions analytiques dans analyse complexe peut ??tre d??finie assez concr??tement par leur d??veloppements en s??rie. D'autre part, dans lambda-calcul, la fonction est un concept primitif, au lieu d'??tre d??fini en termes de la th??orie des ensembles. Les termes transformation et cartographie sont souvent synonyme de fonction. Dans certains contextes, cependant, ils diff??rent l??g??rement. Dans le premier cas, la transformation terme se applique g??n??ralement aux fonctions dont les entr??es et les sorties sont des ??l??ments d'un m??me ensemble ou une structure plus g??n??rale. Ainsi, on parle de transformations lin??aires d'un espace vectoriel dans lui-m??me et de sym??trie transformations d'un objet g??om??trique ou un motif. Dans le second cas, utilis?? pour d??crire des ensembles dont la nature est arbitraire, la cartographie du terme est le concept le plus g??n??ral de la fonction.

Les fonctions math??matiques sont souvent d??sign??s par des lettres, et la notation standard pour la sortie d'une fonction ?? avec l'entr??e x est f (x). Une fonction peut ??tre d??finie que pour certains intrants, et la collecte de toutes les entr??es acceptables de la fonction est appel??e son domaine. L'ensemble de toutes les sorties r??sultant est appel?? gamme de la fonction. Cependant, dans de nombreux domaines, il est ??galement important de pr??ciser le codomain d'une fonction, qui contient la plage, mais ne est pas n??cessairement ??gale. La distinction entre la plage et codomaine nous permet de se demander si les deux se trouvent ??tre ??gales, ce qui dans certains cas peut ??tre une question d'un certain int??r??t math??matique.

Par exemple, l'expression de ?? (x) = x ² d??crit une fonction f d'une variable x, qui, en fonction du contexte, peuvent ??tre un nombre entier , un r??el ou complexe m??me nombre ou un ??l??ment d'un groupe . Pr??cisons que x est un entier; alors cette fonction concerne chaque entr??e, x, avec une seule sortie, x ^2, x obtenue ?? partir de quadrature. Ainsi, l'entr??e 3 est reli??e ?? la sortie 9, dont l'entr??e 1 ?? la sortie 1, et l'entr??e de -2 ?? la sortie 4, et on ??crit ?? (3) = 9, ?? (1) = 1, ?? (-2) = 4. Depuis tout entier peut ??tre carr??, le domaine de cette fonction se compose de tous les entiers, tandis que sa gamme est l'ensemble des carr??s parfaits. Si nous choisissons entiers que le codomaine ainsi, nous constatons que de nombreux num??ros, tels que 2, 3, et 6, sont dans l'ensemble d'arriv??e mais non la gamme.

Ce est une pratique habituelle en math??matiques d'introduire des fonctions temporaires avec des noms comme ??; dans le paragraphe suivant nous pourrions d??finir ?? (x) = 2 x 1, puis ?? (3) = 7. Quand un nom pour la fonction ne est pas n??cessaire, souvent la forme y = x ² est utilis??.

Si nous utilisons une fonction souvent, nous pouvons lui donner un nom plus permanente comme, par exemple,

La propri??t?? essentielle d'une fonction est que, pour chaque entr??e, il doit y avoir une sortie unique. Ainsi, par exemple, la formule

ne d??finit pas une fonction d'une variable r??elle positive, car elle attribue deux sorties ?? chaque num??ro: les racines carr??es de 9 sont 3 et -3. Pour rendre la racine carr??e d'une fonction, il faut pr??ciser ce qui racine carr??e de choisir. La d??finition

pour toute entr??e positive choisit la racine carr??e positive comme une sortie.

Comme mentionn?? ci-dessus, une fonction ne implique pas n??cessairement des nombres. A titre d'exemples, consid??rer la fonction qui associe ?? chaque mot sa premi??re lettre ou la fonction qui associe ?? chaque triangle sa zone.

D??finitions

Comme les fonctions sont utilis??es dans de nombreux domaines des math??matiques, et de tant de mani??res diff??rentes, pas de d??finition unique de la fonction a ??t?? universellement adopt??e. Certaines d??finitions sont ??l??mentaires, tandis que d'autres utilisent un langage technique qui peut obscurcir la notion intuitive. N??anmoins, l'id??e essentielle est la m??me dans toute d??finition.

Une d??finition ??l??mentaire est que

• Une fonction est donn??e par une expression arithm??tique d??crivant comment une nombre d??pend de l'autre.

Un exemple d'une telle fonction est y = 5 x 16 -20 x ³ x ^5, o?? la valeur de y d??pend de la valeur de x. Ce est tout ?? fait satisfaisante pour les parties des math??matiques ??l??mentaires, mais est trop maladroit et restrictive pour les zones plus avanc??es. Par exemple, le cosinus fonction utilis??e dans la trigonom??trie ne peut pas ??tre ??crit de cette mani??re; le mieux que nous pouvons faire, ce est un s??rie infinie,

Cela dit, si nous sommes pr??ts ?? accepter s??rie comme un sens large de ??expression arithm??tique", nous avons une d??finition qui a servi math??matiques raisonnablement bien pendant des centaines d'ann??es.

Finalement, la transformation progressive de "calcul" intuitive dans "analyse" formelle a la n??cessit?? d'une d??finition plus large. L'accent se est d??plac?? de la fa??on dont une fonction a ??t?? pr??sent?? - comme une formule ou une r??gle - ?? un concept plus abstrait. Une partie de la nouvelle fondation ??tait l'utilisation de jeux , de sorte que les fonctions ne sont plus limit??s aux num??ros. Ainsi nous pouvons dire que

• Une fonction f d'un ensemble X ?? un ensemble Y associ??s ?? chaque ??l??ment x de X un ??l??ment y = f (x) dans Y.

Notez que X et Y ne doit pas n??cessairement ??tre diff??rents ensembles; il est possible d'avoir une fonction d'un ensemble ?? lui-m??me. Bien qu'il soit possible d'interpr??ter le terme ??associ??s?? ?? cette d??finition avec une r??gle concr??te pour l'association, il est essentiel d'aller au-del?? de cette restriction. Par exemple, nous pouvons parfois prouver qu'une fonction de certaines propri??t??s existe, mais ne pas ??tre en mesure de donner une r??gle explicite pour l'association. En fait, dans certains cas, il est impossible de donner une r??gle explicite y produire un sp??cifique pour chaque x, m??me si une telle fonction existe. Dans le cadre des fonctions d??finies sur des ensembles arbitraires, il ne est m??me pas clair comment l'expression "r??gle explicite" doit ??tre interpr??t??e.

Comme fonctions prennent de nouveaux r??les et de trouver de nouveaux usages, la relation de la fonction des ensembles n??cessite plus de pr??cision. Peut-??tre que chaque ??l??ment Y est associ??e ?? certains x, peut-??tre pas. Dans certaines parties des math??matiques, y compris la th??orie et la r??cursivit?? analyse fonctionnelle, il est commode pour autoriser les valeurs de x sans association (dans ce cas, le terme fonction partielle est souvent utilis??). Pour ??tre en mesure de discuter de telles distinctions, de nombreux auteurs r??partis en fonction en trois parties, chacune un ensemble:

• Une fonction f est un triplet ordonn?? d'ensembles (F, X, Y) avec des restrictions, o??

  F (graphique) est un ensemble de couples (x, y),

  X (la source) contient tous les premiers ??l??ments de F et peut-??tre plus, et

  Y (la cible) contient tous les ??l??ments du deuxi??me F et peut-??tre plus.

Les restrictions les plus courantes sont que F x paires chacun avec un seul y, et que X est simplement l'ensemble des premiers ??l??ments de F et pas plus.

En l'absence de restrictions sont plac??es sur F, nous parlons d'un relation entre X et Y, plut??t qu'une fonction. La relation est ???? valeur unique" lorsque la premi??re restriction se applique: (x, y ₁₎ ∈ F (x, y ₂₎ ensemble implique ∈ F y ₁ = y _2. Relations qui ne sont pas une valeur unique sont parfois appel??s fonctions multiples. Une relation est "totale" lorsqu'une deuxi??me restriction est titulaire: si x ∈ X alors (x, y) ∈ F pour une y. Ainsi, nous pouvons ??galement dire que

• Une fonction de X ?? Y est une valeur unique, la relation totale entre X et Y.

La gamme de F, et ??, est l'ensemble de toutes les secondes ??l??ments de F; il est souvent d??sign?? par RNG ??. Le domaine de F est l'ensemble de tous les premiers ??l??ments de F; il est souvent d??sign?? par dom ??. Il ya deux d??finitions communes pour le domaine de la ?? certains auteurs d??finissent comme le domaine de F, tandis que d'autres la d??finissent comme la source de F.

La cible de ?? Y est aussi appel?? le codomaine de ??, not??e par la morue ??; et la gamme de ?? est aussi appel?? l'image de ??, d??sign?? par ?? im. Le ?? de notation: X → Y indique que ?? est une fonction avec le domaine X et Y codomaine.

Certains auteurs omettent la source et la cible des donn??es inutiles. En effet, ??tant donn?? que le graphique F, on peut construire une triple appropri?? en prenant dom F ?? la source et rng F ?? la cible; ce qui provoque automatiquement F soit totale. Cependant, la plupart des auteurs en math??matiques avanc??s pr??f??rent la plus grande puissance d'expression conf??r??e par le triple, en particulier la distinction entre elle permet gamme et codomaine.

Incidemment, les paires et triplets ordonn??s que nous avons utilis??es ne sont pas distinctes de jeux; nous pouvons facilement les repr??senter au sein de la th??orie des ensembles. Par exemple, on peut utiliser {{x}, {x, y}} pour le couple (x, y). Ensuite, pour un triplet (x, y, z), on peut utiliser le couple ((x, y), z). Une construction important est le Produit cart??sien d'ensembles X et Y, not??e X ?? Y, qui est l'ensemble de toutes les paires possibles command?? (x, y) avec x ∈ X et y ∈ Y. Nous pouvons ??galement construire l'ensemble de toutes les fonctions possibles du jeu X pour mettre Y, que nous noterons soit [X → Y] ou Y ^X.

Nous avons maintenant une grande flexibilit??. En utilisant des paires pour X nous pouvons traiter, dire la soustraction de nombres entiers en fonction, sous: Z ?? Z → Z. En utilisant paires Y nous pouvons tirer une courbe plane en utilisant une fonction, crv: R → R ?? R. Dans l'intervalle unit??, je, nous pouvons avoir une fonction d??finie comme l'un des nombres rationnels et ?? z??ro autrement, rat: I → 2. En utilisant les fonctions de X nous pouvons consid??rer une int??grale d??finie sur l'intervalle de l'unit?? pour ??tre une fonction, int: [I → R] → R.

Pourtant, nous ne sommes pas encore satisfaits. Nous pouvons voulons encore plus g??n??rale, comme une fonction dont l'int??grale est un fonction de l'??tape; Ainsi, nous d??finissons le soi-disant fonctions g??n??ralis??es. Nous pourrions moins g??n??ralit??, comme une fonction nous pouvons toujours utiliser effectivement pour obtenir une r??ponse d??finitive; Ainsi, nous d??finissons fonctions r??cursives primitives et puis nous limiter ?? ceux que nous pouvons prouver sont effectivement calculable. Ou nous pouvons vouloir porter d??finit pas seulement, mais les structures alg??briques , compl??te avec des op??rations; Ainsi, nous d??finissons homomorphismes.

Histoire

L'histoire de la notion de fonction en math??matiques est d??crit par da Ponte (1992). En terme math??matique, ??fonction?? a ??t?? invent?? par Leibniz en 1694, pour d??crire une quantit?? li??e ?? une courbe , par exemple une courbe de pente ?? un particulier Point. Les fonctions Leibniz consid??r??e sont aujourd'hui appel?? fonctions diff??rentiables . Pour ce type de fonction, on peut parler de limites et d??riv??s ; les deux sont des mesures de la production ou la variation de la sortie car elle d??pend de l'entr??e ou de la modification de l'entr??e. Ces fonctions sont la base de calcul .

La fonction de mot a ??t?? utilis?? plus tard par Leonhard Euler au cours de la mi-18??me si??cle pour d??crire une expression ou une formule impliquant divers arguments, par exemple ?? (x) = sin (x) + x ^3.

Pendant le 19??me si??cle, les math??maticiens ont commenc?? ?? formaliser toutes les diff??rentes branches des math??matiques. Weierstrass pr??conis?? la construction tartre sur l'arithm??tique plut??t que sur la g??om??trie , ce qui a favoris?? la d??finition d'Euler sur Leibniz (voir arithm??tisation de l'analyse).

Au d??but, l'id??e d'une fonction ??tait plut??t limit??e. Joseph Fourier, par exemple, affirm?? que chaque fonction a eu un s??rie de Fourier, quelque chose qu'aucun math??maticien pr??tendre aujourd'hui. En ??largissant la d??finition des fonctions, les math??maticiens ont pu ??tudier des objets math??matiques "??tranges", comme fonctions continues qui sont nulle part diff??rentiables. Ces fonctions ont d'abord ??t?? pens?? pour ??tre seulement curiosit??s th??oriques, et ils ont ??t?? appel??s collectivement "monstres" pas plus tard que la fin du 20??me si??cle. Cependant techniques, de puissants analyse fonctionnelle ont montr?? que ces fonctions sont en quelque sorte ??plus commun?? que les fonctions diff??rentiables. Ces fonctions ont depuis ??t?? appliqu??e ?? la mod??lisation de ph??nom??nes physiques tels que Mouvement brownien.

Vers la fin du 19??me si??cle, les math??maticiens ont commenc?? ?? formaliser toutes les math??matiques ?? l'aide de la th??orie des ensembles , et ils ont cherch?? ?? d??finir chaque objet math??matique comme un d??finir. Dirichlet et Lobachevsky sont traditionnellement cr??dit?? de donner ind??pendamment la d??finition moderne ??formelle?? d'une fonction comme une relation dans laquelle chaque premier ??l??ment a un second ??l??ment unique, mais la demande de Dirichlet ?? cette formalisation est contest??e par Imre Lakatos:

Il n'y a pas une telle d??finition dans les ??uvres de Dirichlet ?? tous. Mais il ya suffisamment de preuves qu'il ne avait aucune id??e de ce concept. Dans son [1837], par exemple, quand il discute des fonctions continues par morceaux, il dit que dans les points de discontinuit?? de la fonction a deux valeurs: ...

(Preuves et R??futations, 151, Cambridge University Press, 1976.)

Hardy (1908, pp. 26-28) d??finie comme une fonction d'une relation entre les deux variables x et y tels que "pour certaines valeurs de x correspond ?? ne importe quel taux valeurs de y." Il requis ni la fonction ?? d??finir pour toutes les valeurs de x, ni d'associer ?? chaque valeur de x pour une seule valeur de y. Cette d??finition large d'une fonction englobe plus que les relations sont ordinairement consid??r??s comme fonctions math??matiques contemporaines.

La notion d'une fonction comme une r??gle pour informatique, plut??t que d'un type particulier de relation, a ??t?? largement ??tudi?? dans la logique math??matique et informatique th??orique. Mod??les pour ces fonctions calculables comprennent la lambda-calcul, le fonctions μ-r??cursives et Machines de Turing.

Vocabulaire

Une entr??e sp??cifique dans une fonction est appel??e un argument de la fonction. Pour chaque valeur de l'argument x, y l'unique correspondant dans le codomaine est appel?? la valeur de fonction en x, ou de la image de x dans ??. L'image de x peut se ??crire f (x) ou y. (Voir la section sur la notation .)

Le graphique d'une fonction f est l'ensemble de toutes couples (x, ?? (x)), pour tout x dans le domaine X. Si X et Y sont des sous-ensembles de R, les nombres r??els, cette d??finition co??ncide avec le sens familier de "graph" comme une image ou un trac?? de la fonction, avec les paires ordonn??es ??tant les coordonn??es cart??siennes de points.

Le concept de l'image peut ??tre ??tendue ?? partir de l'image d'un point de l'image d'un d??finir. Si A est tout sous-ensemble du domaine, puis ?? (A) est le sous-ensemble de la gamme compos??e de toutes les images d'??l??ments de A. On dit ?? (A) est l'image de A sous f.

Notez que la gamme de ?? est le ?? de l'image (X) de son domaine, et que la gamme de ?? est un sous-ensemble de son codomaine.

Le pr??image (ou une image inverse, ou plus pr??cis??ment, image compl??te inverse) d'un sous-ensemble B de la codomain Y sous une fonction ?? est le sous-ensemble du domaine d??fini par X

Ainsi, par exemple, la pr??-image de {4, 9} sous la fonction d'??l??vation au carr?? est l'ensemble {-3, -2, + 2, + 3}.

En g??n??ral, la pr??-image d'un singleton (un ensemble avec un seul ??l??ment) peut contenir ne importe quel nombre d'??l??ments. Par exemple, si ?? (x) = 7, puis l'image r??ciproque de {5} est l'ensemble vide, mais l'image r??ciproque de {7} est l'ensemble du domaine. Ainsi, la pr??-image d'un ??l??ment dans le codomaine est un sous-ensemble du domaine. La convention habituelle sur l'image r??ciproque d'un ??l??ment est que ?? ^-1 (b) des moyens ?? ^-1 ({b}), c.-??-

Trois types importants de la fonction sont les injections (ou un-??-un), qui ont la propri??t?? que si ?? (a) = f (b), puis un must ??gale b; la surjections (ou sur les fonctions), qui ont la propri??t?? que, pour chaque y dans le codomaine il existe un x dans le domaine de telle sorte que f (x) = y; et le bijections, qui sont tous les deux un-??-un et sur. Cette nomenclature a ??t?? introduit par le Groupe Bourbaki.

Lorsque la premi??re d??finition de la fonction donn??e ci-dessus est utilis??, depuis le codomaine ne est pas d??fini, le "surjection" doit ??tre accompagn??e d'une d??claration sur l'ensemble de la fonction cartes sur. Par exemple, nous pourrions dire cartes ?? sur l'ensemble des nombres r??els.

Restrictions et extensions

Officieusement, un restriction d'une fonction ?? est le r??sultat de la coupe de son domaine.

Plus pr??cis??ment, si ?? est une fonction d'un X ?? Y, et S est ne importe quel sous-ensemble de X, la restriction de ?? pour S est la fonction f | _S de S ?? Y de sorte que ?? | _S (S) = ?? (s ) pour tous les s en S.

Si g est toute restriction de ??, nous disons que ?? est une extension de g.

Notation

Il est courant d'omettre les parenth??ses autour de l'argument quand il ya peu de chance d'ambigu??t??, donc: sin x. Dans certains contextes formels, l'utilisation de notation polonaise inverse, x ??, ??limine la n??cessit?? pour toutes les parenth??ses; et, par exemple, la factorielle fonction est toujours ??crite n!, m??me si sa g??n??ralisation, le fonction gamma, est ??crit Γ (n).

Description formelle d'une fonction implique g??n??ralement le nom de la fonction, son domaine, son codomaine, et une r??gle de correspondance. Ainsi, nous voyons souvent une notation en deux parties, un exemple ??tant

o?? la premi??re partie est lu:

• "Ƒ est une fonction de N ?? R" (on ??crit souvent de mani??re informelle "Laissez ??: X → Y?? signifie ??Let ?? ??tre une fonction de X ?? Y"), ou
• "Ƒ est une fonction sur N dans R", ou
• "Ƒ est une fonction de R -??valu??es d'un N ?? valeurs variable",

et la deuxi??me partie est lu:

• cartes ??

Ici, la fonction nomm??e "??" a les nombres naturels comme domaine, les nombres r??els que codomain et cartes n de se divis?? par π. Moins formellement, ce long formulaire peut ??tre abr??g??

mais avec une certaine perte d'informations; nous ne sommes plus explicitement donn?? le domaine et codomaine. M??me la forme longue ici abr??ge le fait que le n sur le c??t?? droit est silencieusement trait?? comme un nombre r??el en utilisant le plongement standard.

Une alternative ?? la notation du c??lon, au moment opportun fonctions sont compos??es, ??crit le nom de la fonction dessus de la fl??che. Par exemple, si ?? est suivie par g, o?? g produit le nombre complexe e ^{i x,} on peut ??crire

Une forme plus ??labor??e de ce est la diagramme commutatif.

Utilisation de ?? (A) identifiant l'image d'un sous-ensemble A ⊆ X est conforme tant qu'aucun sous-ensemble du nom de domaine est ??galement un ??l??ment de nom de domaine. Dans certains domaines (par exemple dans la th??orie des ensembles, o?? ordinaux sont aussi des ensembles de ordinaux), il est commode ou m??me n??cessaire de distinguer les deux concepts; la notation habituelle est ?? [A] pour l'ensemble {?? (x): x ∈ A}; certains auteurs ??crivent ??` x au lieu de f (x), et ??`` ?? A au lieu de [A].

Composition de Fonction

La composition de la fonction de deux ou plusieurs fonctions utilise la sortie d'une fonction que l'entr??e de l'autre. Par exemple, f (x) = sin (x ²⁾ est la composition de la fonction sinus et la fonction d'??l??vation au carr??. Les fonctions ??: X → Y et g: Y → Z peuvent ??tre compos??es en appliquant d'abord ?? ?? un argument x pour obtenir y = ?? (x) et en appliquant ensuite g ?? y obtenir z = g (y). La fonction composite form?? de cette mani??re ?? partir de g ?? g??n??ral et peut se ??crire

La fonction sur la droite agit d'abord et la fonction sur la gauche agit secondes, renversant l'anglais ordre de lecture. Nous nous souvenons de l'ordre par la lecture de la notation comme ??g de ??". L'ordre est important, parce que rarement pouvons-nous obtenir le m??me r??sultat dans les deux sens. Par exemple, supposons que f (x) = x ² g (x) = x 1. Ensuite g (f (x)) = x ² + 1, alors que f (g (x)) = (x 1) ^2, qui est ² x 2 x 1, une fonction diff??rente.

la fonction d'identit??

La fonction unique sur un ensemble X qui mappe chaque ??l??ment se est appel??e la fonction d'identit?? pour X, et g??n??ralement d??sign?? par id _X. Chaque jeu a sa propre fonction d'identit??, donc l'indice ne peut ??tre omise sauf si l'ensemble peut ??tre d??duite ?? partir du contexte. Sous la composition, une fonction d'identit?? est ??neutre??: si ?? est une fonction de X ?? Y, puis

Fonction inverse

Si ?? est une fonction de X ?? Y alors une fonction inverse pour ??, d??sign?? par ?? ^-1, est une fonction dans la direction oppos??e, de Y ?? X, avec la propri??t?? que d'un aller-retour (une composition ) retourne chaque ??l??ment lui-m??me. Non chaque fonction a un inverse; ceux qui le font sont appel??s inversible.

Comme un exemple simple, si ?? convertit une temp??rature en degr??s Celsius ?? des degr??s Fahrenheit, la fonction de conversion degr??s Fahrenheit en degr??s Celsius serait une ^-1 ?? appropri??.

La notation pour la composition nous rappelle de la multiplication; En fait, parfois on note ?? l'aide de la juxtaposition, g ??, sans cercle intervenir. En vertu de cette analogie, fonctions d'identit?? sont comme une, et inverses sont comme inverses (d'o?? la notation).

Sp??cifiant une fonction

Une fonction peut ??tre d??finie par ne importe quelle condition math??matique relative ?? chaque param??tre la valeur de sortie correspondant. Si le domaine est fini, une fonction ?? peut ??tre d??finie par tabulation simplement tous les arguments x et leurs valeurs correspondantes de la fonction ?? (x). Plus g??n??ralement, une fonction est d??finie par une formule , ou (plus g??n??ralement) un algorithme - une recette qui raconte comment calculer la valeur de ?? (x) donn?? aucun ??l??ment x dans le domaine.

Il ya beaucoup d'autres fa??ons de d??finir les fonctions. Des exemples comprennent r??cursivit??, ou alg??brique analytique fermeture, limites , prolongement analytique, infini s??rie, et que les solutions ?? int??grales et diff??rentielles ??quations . Le lambda-calcul fournit un puissant et flexible syntaxe pour la d??finition et la combinaison des fonctions de plusieurs variables.

Calculabilit??

Fonctions qui envoient entiers en entiers ou des cha??nes finies ?? finie, cordes, peuvent parfois ??tre d??finis par un algorithme , qui donne une description pr??cise d'un ensemble d'??tapes de calcul de la sortie de la fonction de son entr??e. Fonctions d??finissables par un algorithme sont appel??s fonctions calculables. Par exemple, le Algorithme d'Euclide permet un proc??d?? pr??cis pour calculer le plus grand commun diviseur de deux nombres entiers positifs. La plupart des fonctions ??tudi??es dans le cadre de la th??orie des nombres sont calculable.

Les r??sultats fondamentaux de th??orie de la calculabilit?? montrent que il ya des fonctions qui peuvent ??tre d??finies avec pr??cision, mais ne sont pas calculable. De plus, dans le sens de la cardinal, presque toutes les fonctions des entiers dans les entiers ne sont pas calculable. Le nombre de fonctions calculables ?? partir des nombres entiers en entiers est d??nombrable, parce que le nombre d'algorithmes possibles est. Le nombre de toutes les fonctions des entiers dans les entiers est plus ??lev??: le m??me que le cardinal des nombres r??els . Ainsi, la plupart des fonctions des entiers dans les entiers ne sont pas calculable. Des exemples sp??cifiques de fonctions incalculable sont connus, y compris la fonction et fonctions de castor affair?? li??e ?? la probl??me de l'arr??t et d'autres probl??mes ind??cidables.

Fonctions avec plusieurs entr??es et sorties

La notion de fonction peut ??tre ??tendu ?? un objet qui prend une combinaison des deux (ou plus) valeurs d'argument ?? un seul r??sultat. Ce concept intuitive est formalis??e par une fonction dont le domaine est le Produit cart??sien de deux ou plusieurs ensembles.

Par exemple, consid??rez la multiplication fonction qui associe deux entiers ?? leur produit: ?? (x, y) = x ?? y. Cette fonction peut ??tre d??fini officiellement comme ayant un domaine de Z ?? Z, l'ensemble de toutes les paires d'entiers; codomain Z; et, pour le graphique, l'ensemble de toutes les paires ((x, y), x ?? y). A noter que le premier composant d'une telle paire est elle-m??me une paire (des entiers), tandis que le second composant est un entier.

La valeur de la fonction de la paire (x, y) est f ((x, y)). Cependant, il est de coutume de d??poser un ensemble de parenth??ses et d'envisager ?? (x, y) une fonction de deux variables (ou avec deux arguments), x et y.

Le concept peut encore ??tre ??tendue en consid??rant une fonction qui produit ??galement une sortie qui est exprim??e en tant que plusieurs variables. Par exemple, consid??rons la fonction de miroir (x, y) = (y, x) avec R x R domaine et codomaine R ?? R ainsi. Le couple (y, x) est une valeur unique dans le codomaine consid??r?? comme un produit cart??sien.

Les op??rations binaires

Le familier op??rations binaires de l'arithm??tique , plus et la multiplication , peuvent ??tre consid??r??s comme des fonctions de R ?? R ?? R. Ce point de vue est g??n??ralis?? dans l'alg??bre abstraite , o?? les fonctions n -aire sont utilis??s pour mod??liser les op??rations de structures alg??briques arbitraires. Par exemple, un r??sum?? groupe est d??fini comme un ensemble X et une fonction ?? de X ?? X ?? X qui satisfait certaines propri??t??s.

Traditionnellement, l'addition et la multiplication sont ??crites dans le notation infix??e: x + y et x ?? y + au lieu de (x, y) et x (x, y).

des espaces de fonction

L'ensemble de toutes les fonctions d'un ensemble X ?? un ensemble Y est not??e X → Y, par [X → Y], ou en Y ^X. Cette derni??re notation est justifi??e par le fait que | Y ^X | = | Y ^| | ^{X |} et est un exemple de la convention de la combinatoire ??num??rative qui fournit des notations pour les jeux en fonction de leurs cardinalit??s.

Voir l'article sur le nombre de cardinaux pour plus de d??tails.

On peut interpr??ter ??: X → Y signifie ?? ∈ [X → Y]; ce est, "?? est une fonction de X ?? Y".

Op??rations ponctuelles

Si ??: X → R et g: X → R sont des fonctions avec X domaine commun et un codomaine commune anneau R, alors on peut d??finir la fonction de somme ?? + g: X → R et la fonction du produit ?? ⋅ g: X → R comme suit:

pour tout x dans X.

Cela transforme l'ensemble de toutes ces fonctions dans un anneau. Les op??rations binaires dans cet anneau ont comme domaine ordonn?? paires de fonctions, et en tant que fonctions codomaine. Ceci est un exemple de monter en abstraction, pour plusieurs types de fonctions complexes.

En prenant une autre structure alg??brique A ?? la place de R, nous pouvons transformer l'ensemble des fonctions de X ?? A dans une structure alg??brique du m??me type d'une mani??re analogue.

Autres propri??t??s

Il ya beaucoup d'autres classes sp??ciales de fonctions qui sont importantes pour certaines branches des math??matiques, ou des applications particuli??res. Voici une liste partielle: