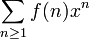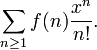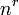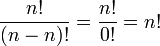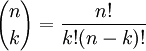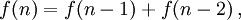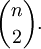Combinatoire

Combinatoire est une branche de math??matiques pures concernant l'??tude des discret (et habituellement finis) objets. Elle est li??e ?? de nombreux autres domaines de math??matiques , comme l'alg??bre , la th??orie des probabilit??s , th??orie ergodique et la g??om??trie , ainsi que des sujets appliqu??s en informatique et la physique statistique. Aspects de la combinatoire comprennent "compter" les objets r??pondant ?? certains crit??res ( combinatoire ??num??rative), de d??cider si les crit??res peuvent ??tre satisfaits, et la construction et l'analyse des objets r??pondant aux crit??res (comme dans mod??les combinatoires et la th??orie des matro??des), trouver des ??plus grands??, ou des objets "plus petite" ??optimales?? ( combinatoire et extr??mes optimisation combinatoire), et de trouver alg??briques structures ces objets peuvent avoir ( combinatoire alg??brique).

Combinatoire est autant ?? r??soudre que le renforcement de la th??orie probl??me, mais il a d??velopp?? de puissantes m??thodes th??oriques, en particulier depuis la fin du XXe si??cle (voir la page Liste des sujets combinatoire pour les d??tails de la mise au point plus r??cente du sujet). Une des parties les plus anciennes et les plus accessibles de la combinatoire est la th??orie des graphes, qui a ??galement de nombreux liens naturels vers d'autres zones.

Il existe de nombreux mod??les combinatoires et th??or??mes li??s ?? la structure de jeux combinatoires. Ces concentrent souvent sur un partition ou partition ordonn??e d'un ensemble. Voir la Liste des sujets de partition pour une liste ??largie de sujets connexes ou sur la Liste des sujets combinatoire pour une liste plus g??n??rale. Certains des r??sultats les plus notables sont mis en ??vidence ci-dessous.

Un exemple d'une question combinatoire simple est la suivante: Quel est le nombre d'ordres possibles d'un jeu de 52 cartes de jeu distinctes? La r??ponse est 52! (52 factorielle ), qui est ??gale ?? environ 8,0658 x 10 ^67.

Un autre exemple d'un probl??me plus difficile: Compte tenu d'un certain nombre n de personnes, est-il possible de les assigner ?? des ensembles de sorte que chaque personne est en au moins un jeu, chaque couple de personnes est dans exactement un jeu ensemble, tous les deux ensembles ont exactement une personne en commun, et aucun ensemble contient tout le monde, tout sauf une personne, ou exactement une seule personne? La r??ponse d??pend de n. Voir ?? th??orie de la conception "ci-dessous.

Combinatoire est fr??quemment utilis?? dans la science de l'ordinateur pour obtenir des estimations sur le nombre d'??l??ments de certains jeux. Un math??maticien qui ??tudie la combinatoire est souvent consid??r?? comme un combinatorialist ou combinatorist.

Histoire de la combinatoire

Utilisations premi??res

L'apparition de la nombre de Fibonacci cinq dans la prosodie. Il ya une fa??on d'organiser un temps, deux ?? deux, trois pour trois, et cinq pour quatre battements.

Les premiers livres sur la combinatoire sont de l'Inde. Un Jainist texte, le Sutra Bhagabati, avait la premi??re mention d'un probl??me de combinatoire; il a demand?? combien de fa??ons on pourrait prendre six go??ts une, deux ou trois go??ts ?? la fois. Le Sutra a ??t?? ??crit autour Bhagabati 300 avant JC, et donc ??tait le premier livre de mentionner la fonction de choix . Les prochaines id??es de combinatoire provenaient Pingala, qui ??tait int??ress?? ?? la prosodie. Plus pr??cis??ment, il a voulu savoir combien de fa??ons un m??tre syllabe six pourrait ??tre fabriqu?? ?? partir de notes courtes et longues. Il a ??crit ce probl??me dans le sutra Chanda (??galement Chandahsutra) dans le deuxi??me si??cle avant JC. En outre, il a aussi trouv?? le nombre de m??tres qui avaient notes n longues et de courtes notes k, ce qui est ??quivalent ?? trouver les coefficients du bin??me.

Les id??es de la Bhagabati ont ??t?? g??n??ralis??es par le math??maticien indien Mahariva en 850 AD, et le travail de Pingala de prosodie a ??t?? ??largi par Bhaskara et Hemacandra en 1100 AD. Bhaskara ??tait la premi??re personne connue ?? trouver la fonction de choix g??n??ralis??e, bien que Brahmagupta peut avoir connu plus t??t. Hemacandra a demand?? combien de m??tres existaient d'une certaine longueur si une longue note a ??t?? consid??r?? comme deux fois plus longtemps que une courte note, qui est ??quivalent ?? trouver les nombres de Fibonacci.

Un Hexagram

Alors que l'Inde ??tait le premier pays ?? publier les r??sultats sur la combinatoire, il y avait d??couvertes par d'autres nations sur des sujets similaires. La premi??re connexion connue ?? combinatoire vient du Papyrus Rhind, probl??me 79, pour la mise en ??uvre d'une s??rie g??om??trique. La prochaine ??tape est d??tenu par le I Ching . Le livre est sur ce que les diff??rents hexagrammes signifient, et pour ce faire, ils avaient besoin de savoir combien il y avait hexagrammes possible. Comme chaque hexagramme est une permutation avec des r??p??titions de six lignes, o?? chaque ligne peut ??tre l'un des deux Etats, solides ou en pointill??s, la combinatoire donne le r??sultat que leur sont 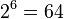hexagrammes. Un moine peut aussi avoir compt?? le nombre de configurations ?? un jeu similaire ?? Aller vers 700 AD. Bien que la Chine avait relativement peu de progr??s dans la combinatoire ??num??rative, ils r??solu un probl??me de conception combinatoire, le carr?? magique , environ 100 AD.

En Gr??ce, Plutarque ??crit que les X??nocrate d??couvert le nombre de diff??rentes syllabes possibles dans la langue grecque. Ceci, cependant, est peu probable parce que ce est l'un des rares mentions de combinatoire en Gr??ce. Le nombre ils ont trouv??, semble ??galement trop rond pour ??tre plus qu'une conjecture. .

Les carr??s magiques sont rest??s un int??r??t de la Chine, et ils ont commenc?? ?? g??n??raliser leur origine 3 ?? 3 carr??s entre 900 et 1300 AD. Chine correspondait avec le Moyen-Orient sur ce probl??me dans le 13??me si??cle. Le Moyen-Orient a ??galement appris ?? propos de coefficients binomiaux de travail indienne, et a trouv?? la connexion ?? l'expansion polynomiale.

Combinatoire de l'Ouest

Combinatoire est arriv?? en Europe au 13??me si??cle par deux math??maticiens, Leonardo Fibonacci et Jordanus Nemorarius. Fibonacci de Liber Abaci introduit beaucoup de l'Arabie et de l'Inde ?? l'Europe des id??es, y compris celle des nombres de Fibonacci. Jordanus ??tait la premi??re personne ?? organiser le coefficient binomial de dans un triangle, comme il le faisait dans la proposition 70 de De Arithmetica. Cela a ??galement ??t?? fait dans le Moyen-Orient en 1265, et la Chine vers 1300. Aujourd'hui, ce triangle est connu comme le triangle de Pascal.

La contribution de Pascal au triangle qui porte son nom vient de son travail sur des preuves formelles ?? ce sujet, en plus de sa connexion entre elle et la probabilit??. Avec Leibniz et ses id??es sur les partitions du 17??me si??cle, ils sont consid??r??s comme les fondateurs de la combinatoire modernes.

Pascal et Leibniz ont compris que l'alg??bre et la combinatoire correspondaient (aka, d??veloppement du bin??me ??tait ??quivalente ?? la fonction de choix.) Cela a ??t?? ??largi par De Moivre, qui a trouv?? l'expansion d'un multinomial. De Moivre a ??galement trouv?? la formule pour d??rangements en utilisant le principe de l'inclusion-exclusion, une m??thode diff??rente de Nikolaus Bernoulli, qui les avait trouv??s pr??c??demment. Il a r??ussi ?? se rapprocher de la coefficients binomiaux et factorielle. Enfin, il a trouv?? une forme ferm??e pour les nombres de Fibonacci en inventant fonctions g??n??ratrices.

Au 18??me si??cle, Euler a travaill?? sur les probl??mes de combinatoire. En plus de travailler sur plusieurs probl??mes de probabilit?? qui pointent vers combinatoire, il a travaill?? sur la Visite chevaliers, Carr?? gr??co-latin, Nombre d'Euler, et autres. Il a ??galement invent?? la th??orie des graphes en r??solvant le Sept ponts de K??nigsberg probl??me, qui entra??nent ??galement la formation de topologie . Enfin, il a innov?? avec partitions de par l'utilisation de fonctions g??n??ratrices.

Combinatoire ??num??rative

Compter le nombre de fa??ons que certains mod??les peuvent ??tre form??s est le probl??me central de la combinatoire ??num??rative. Deux exemples de ce type de probl??me comptent combinaisons et permutations comptant (comme discut?? dans la section pr??c??dente). Plus g??n??ralement, compte tenu d'une collection d'ensembles finis infini {S _i} index??s par les nombres naturels , combinatoire ??num??rative cherche ?? d??crire une fonction de comptage qui compte le nombre d'objets par S _n pour tout n. Bien que comptant le nombre d'??l??ments dans un ensemble est un assez large probl??me math??matique, bon nombre des probl??mes qui se posent dans les applications ont une description relativement simple combinatoire.

Les plus simples de ces fonctions sont formules ferm??es, qui peuvent ??tre exprim??es comme une composition de fonctions ??l??mentaires telles que factorielles , les pouvoirs, et ainsi de suite. Par exemple, comme montr?? ci-dessous, le nombre des diff??rents ordres possibles d'un jeu de n cartes est f (n) = n!. Souvent, aucune forme ferm??e est initialement disponible. Dans ces cas, nous avons fr??quemment premier d??rivons une relation de r??currence, puis r??soudre la r??currence d'arriver ?? la forme ferm??e souhait??e.

Enfin, f (n) peut ??tre exprim?? par un s??ries formelles, appel?? son fonction g??n??ratrice, ce qui est le plus souvent le navigateur fonction ordinaire de production

ou la fonction g??n??ratrice exponentielle

Souvent, une formule ferm??e compliqu?? donne peu d'indications sur le comportement de la fonction de comptage du nombre d'objets compt??s grandit. Dans ces cas, une simple rapprochement asymptotique peut ??tre pr??f??rable. Une fonction 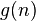est une approximation asymptotique 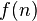si comme l'infini . Dans ce cas, nous ??crivons .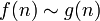

Une fois d??termin??, la fonction g??n??ratrice peut permettre d'extraire toutes les informations donn??es par les approches pr??c??dentes. En outre, les diff??rentes op??rations naturelles sur les fonctions g??n??ratrices telles que l'addition, la multiplication, la diff??renciation, etc., ont une signification combinatoire; Ceci permet de prolonger les r??sultats d'une probl??me combinatoire afin de r??soudre les autres.

Permutations avec r??p??titions

Quand l'ordre est important, et un objet peut ??tre choisie plus d'une fois, le nombre de permutations est

o?? n est le nombre d'objets ?? partir de laquelle vous pouvez choisir et R est le nombre d'??tre choisi.

Par exemple, si vous avez les lettres A, B, C et D et vous souhaitez d??couvrir le nombre de fa??ons de les organiser en trois configurations de lettres ( trigrammes)

1. questions d'ordre (par exemple, AB est diff??rent de BA, les deux sont inclus que les possibilit??s)
2. un objet peut ??tre choisie plus d'une fois (AA possible)

vous trouverez qu'il ya ³ ou 4 64 fa??ons. Ce est parce que pour la premi??re tranche, vous pouvez choisir l'une des quatre valeurs, pour la deuxi??me fente, vous pouvez choisir l'un des quatre, et la fente finale, vous pouvez choisir l'une des quatre lettres. Les multipliant ensemble donne le total.

Permutations sans r??p??titions

Lorsque les questions d'ordre et chaque objet peut ??tre s??lectionn?? seulement une fois, puis le nombre de permutations est

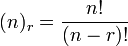o?? n est le nombre d'objets ?? partir de laquelle vous pouvez choisir, r est le nombre ?? ??tre choisi et "!" est le symbole standard signifie factorielle .

Par exemple, si vous avez cinq personnes et allez choisir trois des ceux-ci, vous aurez 5 / (5-3)! = 60 permutations.

Notez que si n = r (qui signifie le nombre d'??l??ments choisis est ??gal au nombre d'??l??ments ?? choisir, cinq personnes et ramasser tous les cinq), la formule devient

o?? 0! = 1.

Par exemple, si vous avez les m??mes cinq personnes et que vous voulez savoir combien de fa??ons que vous pouvez les organiser, il serait 5! ou 5 ?? 4 ?? 3 ?? 2 ?? 1 = 120 fa??ons. La raison pour cela est que vous pouvez choisir parmi 5 pour l'emplacement initial, alors vous ??tes de gauche avec seulement 4 ?? choisir pour la deuxi??me fente, etc. les multipliant ensemble donne le total de 120.

Combinaisons sans r??p??titions

Lorsque l'ordre n'a pas d'importance et chaque objet peut ??tre choisi qu'une seule fois, le nombre de combinaisons est le coefficient binomial :

o?? n est le nombre d'objets ?? partir de laquelle vous pouvez choisir et K est le nombre d'??tre choisi.

Par exemple, si vous avez dix chiffres et souhaitez choisir 5 vous auriez 10 / (5 (10 -! 5))! = 252 fa??ons de choisir. Le coefficient binomial est aussi utilis?? pour calculer le nombre de permutations ?? une loterie.

Combinaisons avec r??p??titions

Lorsque l'ordre n'a pas d'importance et un objet peut ??tre choisie plus d'une fois, le nombre de combinaisons est

o?? n est le nombre d'objets ?? partir de laquelle vous pouvez choisir et K est le nombre d'??tre choisi.

Par exemple, si vous avez dix types de beignets (n) sur un menu ?? choisir et vous voulez trois beignets (k) il ya (10 + 3-1)! / 3 (10 - 1)! = 220 fa??ons de choisir (voir aussi multiset).

Nombres de Fibonacci

Soit f (n) le nombre de sous-ensembles distincts de l'ensemble qui ne contiennent pas deux entiers cons??cutifs. Lorsque n = 4, on a les ensembles {}, {1}, {2}, {3}, {4}, {1,3}, {1,4}, {2,4}, de sorte que f (4 ) = 8. Nous comptons les sous-ensembles souhait??s de 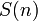en comptant s??par??ment ces sous-ensembles qui contiennent ??l??ment et ceux qui ne le font pas. Si un sous-ensemble contient , Alors elle ne contient pas d'??l??ment 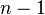. Donc, il ya exactement 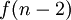des sous-ensembles qui contiennent ??l??ment souhait??s . Le nombre de sous-ensembles qui ne contiennent pas est tout simplement . 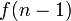L'ajout de ces chiffres ensemble, nous obtenons la relation de r??currence:

o?? et .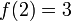

D??s 1202, Leonardo Fibonacci ??tudi?? ces chiffres. Ils sont maintenant appel??s nombres de Fibonacci ; en particulier, 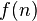qui est connu comme le e nombre de Fibonacci. Bien que la relation de r??currence permet de calculer chaque nombre de Fibonacci, le calcul est inefficace. Toutefois, en utilisant des techniques classiques pour r??soudre relations r??currence, nous pouvons atteindre le ferm??e solution de formulaire:

o?? 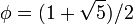, Le nombre d'or .

Dans l'exemple ci-dessus, une approximation asymptotique ?? 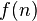est:

lorsque n devient grand.

Combinatoire structurels

Th??orie des graphes

Les graphiques sont des objets de base de la combinatoire. Les questions vont de comptage (par exemple le nombre de graphes sur n sommets avec des bords k) ?? la structure (par exemple, qui contiennent des graphiques Cycles hamiltoniens).

th??orie de la conception

Un r??sultat simple dans le bloc la zone de designs de la combinatoire est que le probl??me des ensembles formant, d??crit dans l'introduction, a une solution seulement si n est de la forme q ² + q + 1. Il est moins simple de prouver qu'il existe une solution si q est un alimentation principale. On suppose que ce sont les seules solutions. Il a ??t?? en outre montr?? que, si une solution ne existe pour q congru ?? 1 ou 2 mod 4, alors q est ??gal ?? une somme de deux nombres carr??s. Ce dernier r??sultat, le Bruck-Ryser th??or??me, est prouv?? par une combinaison de m??thodes constructives sur la base un corps fini et une application de formes quadratiques.

Quand il existe une telle structure, il est appel?? un fini plan projectif; montrant ainsi comment g??om??trie et combinatoire finie croisent.

Th??orie Matroid

Th??orie Matroid abstraction partie de la g??om??trie . Il ??tudie les propri??t??s des ensembles (g??n??ralement, ensembles finis) de vecteurs dans un espace vectoriel qui ne d??pendent pas sur les coefficients particuliers dans un relation de d??pendance lin??aire. Non seulement la structure, mais ??galement des propri??t??s ??num??ratives appartiennent ?? matro??de th??orie.

Par exemple, ??tant donn?? un ensemble de n vecteurs dans l'espace euclidien , ce est le plus grand nombre d' avions qu'ils peuvent g??n??rer? R??ponse: le coefficient binomial

Y at-il un ensemble qui g??n??re exactement un plan sensiblement? (Non, dans presque tous les cas.) Ce sont des questions extr??mes en g??om??trie, comme on le verra ci-dessous.

Extremal et la combinatoire probabilistes

Beaucoup de questions extr??mes face ?? syst??mes fixes. Un exemple simple est la suivante: quel est le plus grand nombre de sous-ensembles d'un n -Element mis l'on peut avoir, si aucun des deux sous-ensembles sont disjoints? R??ponse: la moiti?? du nombre total de sous-ensembles. Preuve: Appelez le n -Element ensemble S. Entre tout sous-ensemble T et son compl??ter S - T, au plus on peut ??tre choisie. Cela prouve le nombre maximum de sous-ensembles choisis ne est pas sup??rieure ?? la moiti?? du nombre de sous-ensembles. Pour montrer l'on peut atteindre la moiti?? du nombre, choisir un ??l??ment x de S et choisir tous les sous-ensembles qui contiennent x.

Un probl??me plus difficile est de caract??riser les solutions extr??mes; dans ce cas, de montrer que pas d'autre choix de sous-ensembles peut atteindre le nombre maximal tout en satisfaisant l'exigence.

Souvent, ce est trop dur, m??me pour trouver le f extr??mal de r??ponse (n) exactement et on ne peut donner une estimation asymptotique.

Th??orie Ramsey

Th??orie Ramsey est une partie c??l??bre de la combinatoire extr??maux. Il stipule que toute suffisamment grande configuration al??atoire contiendra un peu d'ordre.

Frank Ramsey se est av??r?? que pour tout entier k il existe un entier n tel que tout graphe ?? n sommets soit contient une clique ou un ensemble ind??pendant de taille k. Ce est un cas particulier de Th??or??me de Ramsey. Par exemple, compte tenu de tout groupe de six personnes, ce est toujours le cas que l'on peut trouver trois personnes sur ce groupe soit se connaissent tous ou ne savez pas ?? l'autre. La cl?? de la preuve dans ce cas est le Pigeonhole Principe: soit A conna??t trois des personnes qui restent, ou A ne sait pas trois des personnes restantes.

Voici une preuve simple: Prenez l'une des six personnes, l'appeler A. Soit A conna??t trois des personnes qui restent, ou A ne sait pas trois des personnes restantes. Supposons que l'ancienne (la preuve est identique si l'on suppose ce dernier). Que les trois personnes que A sait ??tre B, C, et D. Maintenant, soit deux personnes de {B, C, D} conna??tre (dans ce cas, nous avons un groupe de trois personnes qui se connaissent - ces deux plus un ) ou aucun de B, C, D conna??tre (dans ce cas, nous avons un groupe de trois personnes qui ne connaissent pas l'autre - B, C, D). CQFD.

Combinatoire extr??mes

Les types de questions abord??es dans ce cas sont de la plus grande possible graphique qui satisfait certaines propri??t??s. Par exemple, le plus grand graphe sans triangle sur les sommets 2n est un graphe complet biparti K _{n, n.}

Combinatoire probabilistes

Voici les questions sont du type suivant: quelle est la probabilit?? d'une certaine propri??t?? de graphe pour un graphe al??atoire (dans une certaine classe) Par exemple ce est le nombre moyen de triangles dans un graphe al??atoire?

Combinatoire g??om??triques

Combinatoire g??om??trique est li??e ?? convexe et g??om??trie discr??te. Il demande, par exemple, combien de faces de chaque dimension peut un polytope convexes ont. Propri??t??s m??triques de polytopes jouent un r??le important ainsi, par exemple la Cauchy th??or??me sur la rigidit?? des polytopes convexes. Polytopes sp??ciaux sont ??galement envisag??es, comme permuto??dre, et Associa??dre Polytope Birkhoff.