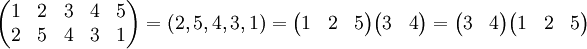Permutation

Dans plusieurs domaines de math??matiques la permutation terme est utilis?? avec des significations diff??rentes, mais ??troitement li??s. Ils se rapportent tous ?? la notion de (r??) organisation ??l??ments d'une donn??e ensemble fini dans une s??quence .

D??finitions

Le concept g??n??ral de permutation peut ??tre d??fini de fa??on plus formelle dans des contextes diff??rents:

Dans combinatoire

En combinatoire , une permutation est g??n??ralement comprise comme une s??quence contenant chaque ??l??ment d'un ensemble fini une fois, et une seule fois. Le concept de la s??quence est diff??rente de celle d'un ensemble, en ce que les ??l??ments d'une s??quence apparaissent dans un certain ordre: la s??quence pr??sente un premier ??l??ment (sauf se il est vide), un deuxi??me ??l??ment (?? moins que sa longueur est inf??rieure ?? 2), et ainsi de suite. En revanche, les ??l??ments d'un ensemble ont pas d'ordre; {1, 2, 3} et {3, 2, 1} sont diff??rentes fa??ons pour d??signer le m??me ensemble.

Toutefois, il existe ??galement une signification plus g??n??rale classique du terme "permutation" utilis??e dans la combinatoire. En ce sens plus g??n??ral, ces permutations sont des s??quences dans lesquelles, comme pr??c??demment, chacun des ??l??ments se produit au plus une fois, mais pas tous les ??l??ments de l'ensemble suivant doivent ??tre utilis??s.

Pour une notion associ??e dans laquelle l'ordre des ??l??ments s??lectionn??s forment un ensemble, dont l'ordre ne est pas pertinent, voir Combinaison.

Dans la th??orie des groupes

Dans la th??orie des groupes et des domaines connexes, les ??l??ments d'une permutation n'a pas besoin d'??tre dispos??s dans un ordre lin??aire, ou m??me dans ne importe quel ordre ?? tous. Selon cette d??finition raffin??e, une permutation est un une bijection de ensemble fini sur lui-m??me. Cela permet la d??finition des groupes de permutations; voir groupe de permutation.

Compter permutations

Dans ce seul article, la d??finition traditionnelle de la combinatoire est utilis??: une permutation est une s??quence ordonn??e d'??l??ments choisis parmi un ensemble fini donn??, sans r??p??titions, et pas n??cessairement en utilisant tous les ??l??ments d'un ensemble donn??. Par exemple, compte tenu de l'ensemble des lettres {C, E, G, I, N, R}, quelques permutations sont RING, RIZ, NICER, r??gne et grincer des dents, mais aussi RNCGI -. La s??quence n'a pas besoin d'??peler un mot existant MOTEUR , d'autre part, ne est pas une permutation, car il utilise des ??l??ments E et N deux fois.

Si n d??signe la taille de l'ensemble - le nombre d'??l??ments disponibles pour la s??lection - et seuls sont consid??r??s les permutations qui utilisent tous les ??l??ments N, alors le nombre total de permutations possibles est ??gal ?? n, o?? "!" est la factorielle op??rateur. Cela peut ??tre d??montr?? de mani??re informelle comme suit. Dans la construction d'une permutation, il existe n choix possibles pour le premier ??l??ment de la s??quence. Une fois qu'il a ??t?? choisi,

les ??l??ments sont ?? gauche, si pour le deuxi??me ??l??ment il n'y a que

choix possibles. Pour les deux premiers ??l??ments, qui nous donne

n ?? (n - 1) permutations possibles.

Pour s??lectionner le troisi??me ??l??ment, il existe alors

??l??ments gauche, donnant, pour les trois premiers ??l??ments,

n ?? (n - 1) ?? (n - 2) permutations possibles.

Continuer ainsi jusqu'?? ce que il n'y a que deux ??l??ments de gauche, il ya deux choix, donnant le nombre de permutations possibles, comprenant des

??l??ments:

n ?? (n - 1) ?? (n - 2) ?? ... ?? 2.

Le dernier choix est maintenant forc??, comme il ya exactement un ??l??ment gauche. Dans une formule, ce est le nombre

n ?? (n - 1) ?? (n - 2) ?? ... ?? 2 ?? 1

(Qui est le m??me que pr??c??demment parce que le facteur 1 ne fait pas de diff??rence). Ce num??ro est, par d??finition, le m??me que n!.

En g??n??ral, le nombre de permutations est d??sign??e par P (n, r), _n P _r, ou parfois O??:

• n est le nombre d'??l??ments pouvant ??tre s??lectionn??s, et
• r est le nombre d'??l??ments ?? s??lectionner (0 ≤ r ≤ n).

Pour le cas o??

il vient d'??tre montr?? que

. Le cas g??n??ral est donn?? par la formule:

Comme pr??c??demment, ceci peut ??tre localis??e de mani??re informelle en consid??rant la construction d'une permutation arbitraire, mais ce temps d'arr??t lorsque la longueur r est atteinte. La construction se d??roule d'abord comme ci-dessus, mais se arr??te ?? longueur r. Le nombre de permutations possibles qui a ??t?? atteint, est:

P (n, r) = n ?? (n - 1) ?? (n - 2) ?? ... ?? (n - r + 1).

Donc:

n! = N ?? (n - 1) ?? (n - 2) ?? ... ?? 2 ?? 1

= N ?? (n - 1) ?? (n - 2) ?? ... ?? (n - r + 1) ?? (n - r) ?? ... ?? 2 ?? 1

= P (n, r) ?? (n - r) ?? ... ?? 2 ?? 1

= P (n, r) ?? (n - r) !.

Mais si n! = P (n, r) ?? (n - r) !, puis

. Par exemple, se il existe un total de 10 ??l??ments et sont s??lection d'une s??quence de trois ??l??ments de cet ensemble, la premi??re est une s??lection ?? partir de 10 ??l??ments, le c??t?? de l'une restante 9, et enfin de la 8 restant, ce qui donne

. Dans ce cas, n = 10 et r = 3. En utilisant la formule pour calculer P (10,3),

Dans le cas particulier o?? n = r la formule ci-dessus se simplifie en:

La raison pour laquelle 0! 1 = 0, ce est que! est un vide produit, qui est toujours ??gal ?? 1.

Dans l'exemple donn?? dans l'en-t??te de cet article, avec 6 entiers {1..6}, ce serait: P (6,6) = 6! / (6-6)! = (1 ?? 2 ?? 3 ?? 4 ?? 5 ?? 6) / 0! = 720/1 = 720.

Les autres notations, ??g??s comprennent ^{le n} P _r, P _{n, r, n} ou P _r. Une notation moderne commun est (n) _r qui est appel?? un tomber factorielle. Cependant, la m??me notation est utilis??e pour la la hausse factorielle (??galement appel?? Symbole Pochhammer)

n (n + 1) (n + 2) ⋯ (n + r - 1) r.

Avec la notation factorielle en hausse, le nombre de permutations est (n - r + 1) _r.

Permutations dans la th??orie des groupes

Comme expliqu?? dans une section pr??c??dente, en th??orie des groupes la permutation terme (d'un ensemble) est r??serv??e ?? un bijection ( bijection) ?? partir d'un ensemble fini sur lui-m??me. L'exemple pr??c??dent, de faire des permutations de num??ros de 1 ?? 10, serait traduit par une carte de l'ensemble {1, ..., 10} pour lui-m??me.

Notation

Il ya deux principales notations pour ces permutations. Dans la notation de relation, on peut juste arranger l'ordre "naturel" des ??l??ments ??tant permut?? sur une ligne, et la nouvelle commande sur une autre ligne:

signifie la permutation s de l'ensemble {1,2,3,4,5} d??finie par s (1) = 2, S (2) = 5, S (3) = 4, s (4) = 3, s (5) = 1.

Si nous avons un ensemble fini E de n ??l??ments, il est par d??finition bijection avec l'ensemble {1, ..., n}, o?? cette bijection f correspond juste pour num??roter les ??l??ments. Une fois qu'ils sont num??rot??s, nous pouvons identifier les permutations de l'ensemble E avec permutations de l'ensemble {1, ..., n}. (En termes plus math??matiques, la fonction qui associe une permutation de E s ?? la permutation de fosof ^-1 {1, ..., n} est un morphisme de la groupe sym??trique de E dans celui de {1, ..., n}, voir ci-dessous.)

Sinon, nous pouvons ??crire la permutation en termes de la fa??on dont les ??l??ments changent lorsque la permutation est successivement appliqu??e. Ceci est d??sign?? comme la d??composition de la permutation dans un produit de disjointe cycles. Il fonctionne comme suit: partant d'un ??l??ment x, nous ??crivons la s??quence (x s (x) s ² (x) ...) jusqu'?? ce que nous serons de retour l'??l??ment de d??part (?? quel point nous fermons la parenth??se sans ??crire pour une deuxi??me fois ). Ceci est appel?? le cycle associ?? ?? x 's orbite suivante s. Puis nous prenons un ??l??ment, nous ne avons pas ??crit encore et faisons la m??me chose, jusqu'?? ce que nous avons consid??r?? tous les ??l??ments. Dans l'exemple ci-dessus, on obtient: s = (2 1 5) (3 4).

Chaque cycle (x ₁ x ₂ ... x _L) signifie que la permutation cartes x _i x _i sur _une (i = 1 ... L -1) et x _L x sur _1, et tous les autres ??l??ments laisse invariante. L est appel??e la dur??e du cycle. ??tant donn?? que ces cycles ont par construction disjoints des supports (ce est ?? dire qu'ils agissent non triviale sur des sous-ensembles disjoints de E), ils ne commutent (par exemple, (1 2 5) (3 4) = (3 4) (2 1 5)). L'ordre des cycles dans le (composition) produit n'a pas d'importance, alors que l'ordre des ??l??ments dans chaque cycles ne importe ( jusqu'?? changement cyclique; voir aussi cycles et points fixes).

De toute ??vidence, un 1 cycle (cycle de longueur 1) est le m??me que la fixation de l'??l??ment qu'il contient, donc il est inutile de l'??crire explicitement. La d??finition de certains auteurs d'un cycle ne incluent pas les cycles de longueur 1.

Cycles de longueur deux sont appel??s transpositions; ces permutations simplement ??changer la place de deux ??l??ments. (A l'inverse, un transposition matricielle est lui-m??me un exemple important d'une permutation.)

Produit et inverse de permutations

On peut d??finir le produit de deux permutations comme suit. Si nous avons deux permutations, P et Q, l'action de la premi??re ex??cution de P et Q sera le m??me que l'ex??cution certaine permutation unique R. Le produit de P et Q est alors d??fini comme ??tant que R permutation. Regarde permutations que bijections, le produit de deux permutations est donc le m??me que leur composition que des fonctions. Il n'y a aucune notation universellement accept??e pour le fonctionnement du produit entre les permutations, et selon l'auteur une formule comme PQ peut signifier soit P ∘ ∘ Q ou Q P. Depuis la composition de fonctions est associative , est donc le fonctionnement du produit sur des permutations: (P ∘ Q) ∘ ∘ R = P (Q ∘ R).

De m??me, ??tant donn?? que bijections ont inverses , alors ne permutations, et les deux P ∘ P et P ^{-1 -1} ∘ P sont la "permutation identit??" (voir ci-dessous) qui laisse toutes les positions inchang??es. Ainsi, on peut voir que les permutations forment un groupe .

Comme pour ne importe quel groupe, il existe un groupe isomorphisme de groupes de permutation, obtenus en attribuant ?? chaque permutation inverse son, et ce est un isomorphisme involution, donnant une double vision sur un r??sultat abstrait. Depuis (P ∘ Q) ^-1 = Q ^-1 ∘ P ^-1, d'un point de vue abstrait il est indiff??rent que PQ repr??sente "P avant Q" ou "P apr??s Q". Pour permutations concr??tes, la distinction est, bien s??r, tout ?? fait mat??riel.

Permutations sp??ciales

Si nous pensons ?? une permutation que ??changements?? la position du premier ??l??ment au premier ??l??ment, la seconde ?? la seconde, et ainsi de suite, nous avons vraiment ne ont pas chang?? les positions des ??l??ments du tout. En raison de son action, nous d??crivons ce que la permutation identit??, car elle agit comme un fonction identit??. Inversement, une permutation qui change la position de tous les ??l??ments (pas d'??l??ment est mapp?? sur lui-m??me) est appel?? un d??rangement.

Si l'on a une certaine permutation, appel?? P, on peut d??crire une permutation, P ^-1 ??crite, qui d??fait l'action de l'application P. En substance, l'ex??cution P alors P ^-1 ??quivaut ?? effectuer la permutation identit??. On a toujours une telle permutation depuis une permutation est une bijection. Une telle permutation est appel?? le permutation inverse. Il est calcul?? en ??changeant chaque num??ro et le num??ro de la place qu'il occupe.

Une m??me permutation est une permutation qui peut ??tre exprim?? comme le produit d'un nombre pair de transpositions, et la permutation est une permutation identit?? m??me si elle est ??gale ?? (1 2) (1 2). Une permutation impaire est une permutation qui peut ??tre exprim?? comme le produit d'un nombre impair de transpositions. Il peut ??tre d??montr?? que chaque permutation est soit pair ou impair et ne peut pas ??tre ?? la fois.

Un th??or??me concernant la permutation inverse est l'effet d'une conjugaison d'une permutation par une permutation dans un groupe de permutation. Si nous avons une permutation Q = ₍₁ i i i ... _{2 n)} et une permutation P, alors RPQ ^-1 = (P (i ₁₎ P (i ₂₎ ... P (i _n)).

Nous pouvons ??galement repr??senter une permutation de matrice forme; la matrice r??sultante est appel??e matrice de permutation.

Permutations en informatique

Certains des anciens manuels Regardons permutations, les affectations, comme mentionn?? ci-dessus. En sciences informatiques termes, ce sont op??rations d'affectation, avec des valeurs

1, 2, ..., n

affect?? aux variables

x _1, x _2, ..., x _n.

Chaque valeur doit ??tre attribu??e qu'une seule fois.

La diff??rence cession / substitution est alors illustre une mani??re dont programmation fonctionnelle et la programmation imp??rative diff??rer - programmation fonctionnelle pure a pas de m??canisme d'affectation. La convention de math??matiques est aujourd'hui que permutations sont juste des fonctions et l'op??ration sur eux est la composition de fonctions ; programmeurs fonctionnels suivent cette. Dans la langue d'affectation une substitution est une instruction pour basculer autour des valeurs attribu??es, simultan??ment; un probl??me bien connu.

Num??rotation permutations

Factoradic num??ros peuvent ??tre utilis??s pour attribuer des num??ros uniques aux permutations, telle que donn??e une factoradic de k, on peut trouver rapidement la permutation correspondante.

Les algorithmes pour g??n??rer des permutations

G??n??ration non ordonn??e

! Pour tout nombre k, avec 0 ≤ k <n, l'algorithme suivant g??n??re une permutation unique de _{la j} de la s??quence initiale, j = 1 ... n:

  la fonction de permutation (k, s) {
      var int factorielle: = 1;
      pour j = 2 ?? la longueur (s) {
         factorial: = * factorielle (j-1);  // Factorielle = (j-1)!
         [la j- ((k / factoriel) mod j)] de swap avec s [j];
      }
      retourner s;
  }

La g??n??ration de l'ordre lexicographique

! Pour tout nombre k, avec 0 ≤ k <n, l'algorithme suivant g??n??re la permutation correspondant lexicographique de _{la j} de la s??quence initiale, j = 1 ... n:

  la fonction de permutation (k, s) {
      int var n: = longueur (s);  factorielle: = 1;
      pour j = 2 ?? n-1 {// calculer (n-1)!
          factorielle: = factorielle * j;
      }
      pour j = 1 ?? N-1 {
          tempj: = (k / factorielle) mod (n + 1- j);
          Temps: = s [j] + tempj
          pour i = j + tempj ?? j + 1 ??tape -1 {
              S [i]: = s [i-1];  // Changer le droit de la cha??ne
          }
          s [j]: = temps;
          factorial: = factorielle / (n- j);
      }
      retourner s;
  }

Notation

• k / j repr??sente la division enti??re de k par j, ce est ?? dire l'int??grale quotient sans reste, et
• k mod j est le reste suit division enti??re de k par j.
• s [n] d??signe le n i??me ??l??ment de la s??quence s.

Impl??mentations logicielles et mat??rielles

Fonctions de calcul

La plupart des calculatrices ont une fonction int??gr??e pour calculer le nombre de permutations, appel?? nPr ou PERM sur un grand nombre. La fonction de permutations ne est souvent disponible ?? travers plusieurs couches de menus; comment acc??der ?? la fonction est g??n??ralement indiqu?? dans la documentation de calculatrices qui le soutiennent.

Les fonctions de tableur

Plus tableur fournit ??galement une fonction int??gr??e pour calculer le nombre de permutations, appel?? PERMUT dans de nombreux tableurs populaires. Apple logiciels Num??ros notamment ne comprend pas actuellement une telle fonction.