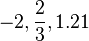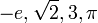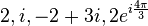Math??matiques
Saviez-vous ...
SOS Enfants, un organisme de bienfaisance de l'??ducation , a organis?? cette s??lection. parrainage SOS enfant est cool!
Math??matiques (famili??rement, math??matiques ou math??matiques) est l'ensemble des connaissances centr??e sur des concepts tels que la quantit?? , la structure, l'espace, et changer, et aussi la discipline acad??mique qui les ??tudie. Benjamin Peirce a appel?? ??la science qui en tire les conclusions n??cessaires". D'autres praticiens des math??matiques soutiennent que les math??matiques sont la science de mod??le, et que les math??maticiens cherchent des patrons se trouve dans le nombre, l'espace, la science, ordinateurs, abstractions imaginaires, ou ailleurs. Math??maticiens explorer ces concepts, visant ?? formuler de nouvelles conjectures et ??tablir leur v??rit?? en rigoureux d??duction choisi de mani??re appropri??e axiomes et d??finitions.
Gr??ce ?? l'utilisation de abstraction et logique raisonnement, les math??matiques ont ??volu?? ?? partir comptage, le calcul, la mesure et l'??tude syst??matique de la formes et mouvements d'objets physiques. Connaissance et utilisation des math??matiques de base ont toujours ??t?? une partie intrins??que et int??grante de la vie individuelle et collective. Raffinements des id??es de base sont visibles dans les textes math??matiques originaires de la Egypte ancienne, M??sopotamienne, indienne , Chinois, Grec et Mondes islamiques. Arguments rigoureux premi??re apparition dans Math??matiques grecques, notamment dans Euclide l ' Elements . Le d??veloppement se est poursuivi en rafales capricieuses jusqu'?? la Renaissance p??riode du 16??me si??cle , lorsque les innovations math??matiques interagi avec le nouveau d??couvertes scientifiques, conduisant ?? une acc??l??ration de la recherche qui se poursuit jusqu'?? nos jours.
Aujourd'hui, les math??matiques sont utilis??es ?? travers le monde dans de nombreux domaines, y compris les sciences naturelles, l'ing??nierie , la m??decine et le sciences sociales telles que l'??conomie . math??matiques appliqu??es , l'application des math??matiques ?? des domaines tels, inspire et fait usage de nouvelles d??couvertes math??matiques et conduit au d??veloppement de nouvelles disciplines parfois enti??rement. Les math??maticiens se engagent aussi dans math??matiques pures, ou math??matiques pour elle-m??me, sans avoir ne importe quelle application ?? l'esprit, bien que les demandes pour ce qui a commenc?? comme les math??matiques pures sont souvent d??couverts plus tard.
??tymologie
Le mot ??math??matiques?? (en grec: μαθηματικά ou mathēmatik??) vient du grec μάθημα (MATHEMA), ce qui signifie l'apprentissage, l'??tude, la science, et de plus est venu d'avoir le sens de "??tude math??matique" plus ??troite et plus technique, m??me ?? l'??poque classique. Son adjectif est μαθηματικός (mathēmatik??s), li??s ?? l'apprentissage, ou studieuse, qui m??me encore venu ?? signifier math??matique. En particulier, μαθηματικὴ τέχνη (mathēmatikḗ TEKHNE), en latin ars Mathematica, signifiait l'art math??matique.
Le pluriel apparente anglais , comme le fran??ais pluriel les math??matiques (et le singulier d??riv?? la math??matique moins couramment utilis??es), remonte ?? la Mathematica pluriel neutre latine ( Cicero), sur la base du μαθηματικά de τα pluriel grec (ta mathēmatik??), utilis?? par Aristote , et qui signifie ?? peu pr??s ??toutes choses math??matique". En anglais, cependant, les math??matiques nominaux prend des formes de verbe au singulier. Il est souvent abr??g?? en math??matiques en langue anglaise en Am??rique du Nord et en math??matiques ailleurs.
Histoire

L'??volution des math??matiques pourrait ??tre consid??r?? comme une s??rie de plus en plus de abstractions, ou encore une expansion de la mati??re. La premi??re abstraction ??tait probablement celui de num??ros . La r??alisation que deux pommes et deux oranges ont quelque chose en commun ??tait une perc??e dans la pens??e humaine. En plus de reconna??tre comment compter des objets physiques, peuples pr??historiques ont ??galement reconnu la fa??on de compter quantit??s abstraites, comme le temps - jour , saisons , ann??es. arithm??tique ( addition , soustraction , multiplication et division ), ont naturellement suivi.
Des mesures suppl??mentaires doivent ??criture ou d'un autre syst??me pour les num??ros d'enregistrement tels que pointages ou les cordes nou??es appel??s quipu utilis?? par l' empire inca pour stocker des donn??es num??riques. num??ral syst??mes ont ??t?? nombreuses et vari??es, avec les chiffres d'abord connus ??crite cr????s par les Egyptiens au Moyen-Uni textes comme la Papyrus Math??matique Rhind.

Depuis les d??buts de l'histoire, les principales disciplines dans les math??matiques d??coulaient de la n??cessit?? de faire des calculs relatifs ?? la fiscalit?? et commerce, de comprendre les relations entre les nombres, mesurer la terre, et de pr??dire des ??v??nements astronomiques . Ces besoins peuvent ??tre plus ou moins li??e ?? la large subdivision des math??matiques dans les ??tudes sur la quantit??, la structure, l'espace, et le changement.
Math??matiques a depuis ??t?? consid??rablement ??tendu, et il ya eu une interaction fructueuse entre les math??matiques et la science, au profit des deux. D??couvertes math??matiques ont ??t?? faites ?? travers l'histoire et continuent d'??tre faite aujourd'hui. Selon Mikhail B. Sevryuk, dans le num??ro de Janvier 2006 de la Bulletin de l'American Mathematical Society, "Le nombre de papiers et de livres inclus dans le Base de donn??es de math??matique avis depuis 1940 (la premi??re ann??e de fonctionnement du MR) est maintenant plus de 1,9 millions d'habitants, et plus de 75 000 articles sont ajout??s ?? la base de donn??es chaque ann??e. L'??crasante majorit?? des ??uvres dans cet oc??an contient de nouvelles math??matiques th??or??mes et leurs preuves ".
Inspiration, les math??matiques pures et appliqu??es, et de l'esth??tique

Math??matiques se pose partout o?? il ya des probl??mes difficiles qui impliquent la quantit??, la structure, l'espace, ou de changement. Au d??but, ils ont ??t?? trouv??s dans commerce, la mesure de terre et plus tard l'astronomie ; de nos jours, toutes les sciences sugg??rent probl??mes ??tudi??s par les math??maticiens, et de nombreux probl??mes se posent dans les math??matiques elles-m??mes. Newton ??tait l'un des inventeurs de calcul infinit??simal, m??me si la quasi-totalit?? de la notation utilis??s dans calcul infinit??simal a ??t?? fourni par Leibniz ?? l'exception d'un point au-dessus d'une variable pour signifier la diff??renciation par rapport au temps. Feynman a invent?? le Int??grante de chemin de Feynman en utilisant une combinaison de raisonnement et de compr??hension de la physique, et aujourd'hui la th??orie des cordes inspire ??galement de nouvelles math??matiques. Certains des math??matiques ne est pertinente que dans la r??gion qui l'a inspir??, et est appliqu?? pour r??soudre d'autres probl??mes dans ce domaine. Mais souvent, les math??matiques inspir?? par une zone se av??re utile dans de nombreux domaines, et rejoint la r??serve g??n??rale des concepts math??matiques. Le fait remarquable que m??me les math??matiques "pure" se av??re souvent avoir des applications pratiques est ce Eugene Wigner a appel?? " la d??raisonnable efficacit?? des math??matiques ".
Comme dans la plupart des domaines d'??tude, l'explosion des connaissances dans l'??re scientifique a conduit ?? une sp??cialisation en math??matiques. Une distinction majeure entre math??matiques pures et math??matiques appliqu??es . Plusieurs domaines des math??matiques appliqu??es ont fusionn?? avec les traditions connexes en dehors des math??matiques et de devenir disciplines dans leur propre droit, y compris des statistiques , la recherche op??rationnelle et informatique .
Pour ceux qui sont math??matiquement inclin??, il ya souvent un aspect esth??tique d??finitive ?? une grande partie de math??matiques. Beaucoup de math??maticiens parlent de l'??l??gance des math??matiques, ses intrins??ques esth??tique et int??rieur beaut??. Simplicit?? et g??n??ralit?? sont ??valu??s. Il ya de la beaut?? dans une d??monstration simple et ??l??gant, comme Euclide preuve d 'qu'il ya une infinit?? de nombres premiers , et dans une m??thode num??rique ??l??gante qui acc??l??re le calcul, comme le transform??e de Fourier rapide. GH Hardy Apologie de math??maticien a exprim?? la conviction que ces consid??rations esth??tiques sont, en eux-m??mes, suffisants pour justifier l'??tude des math??matiques pures. Les math??maticiens se efforcent souvent de trouver des preuves de th??or??mes qui sont particuli??rement ??l??gante, une qu??te Paul Erdős souvent d??sign?? comme trouver des preuves de "Le Livre" dans lequel Dieu avait ??crit ses preuves pr??f??r??s. La popularit?? de math??matiques r??cr??atives est un autre signe du plaisir beaucoup trouvent dans la r??solution de questions math??matiques.
Notation, la langue, et la rigueur

La plupart de la notation math??matique en usage aujourd'hui n'a pas ??t?? invent?? jusqu'?? ce que le 16??me si??cle . Avant cela, les math??matiques a ??t?? ??crit en mots, un processus laborieux qui limitait d??couverte math??matique. Dans le 18??me si??cle , Euler ??tait responsable de la plupart des notations en usage aujourd'hui. Notation moderne rend les math??matiques beaucoup plus facile pour les professionnels, mais les d??butants trouvent souvent intimidante. Il est tr??s comprim??: quelques symboles contiennent une grande quantit?? d'informations. Comme la notation musicale, la notation math??matique moderne dispose d'une syntaxe stricte et encode l'information qu'il serait difficile d'??crire de toute autre mani??re.
Math??matique langue est ??galement difficile pour les d??butants. Des mots tels que ou et seulement avoir un sens plus pr??cis que dans le langage courant. Confondant aussi aux d??butants, des mots tels que ouvert et domaine ont ??t?? donn?? significations math??matiques sp??cialis??es. Jargon math??matique comprend des termes techniques tels que hom??omorphisme et int??grable. Mais il ya une raison pour la notation sp??ciale et le jargon technique: les math??matiques n??cessite plus de pr??cision que le langage courant. Les math??maticiens se r??f??rent ?? cette pr??cision du langage et de la logique ??rigueur??.
Rigueur est fondamentalement une question de preuve math??matique . Les math??maticiens veulent que leurs th??or??mes de suivre des axiomes par des moyens de raisonnement syst??matique. Ce est pour ??viter erron??es " th??or??mes ??, bas??s sur des intuitions faillibles, dont de nombreux cas se sont produits dans l'histoire de l'objet. Le niveau de rigueur pr??vu en math??matiques a vari?? au fil du temps: les Grecs devraient arguments d??taill??s, mais au moment de Isaac Newton les m??thodes employ??es ??taient moins rigoureux. Probl??mes inh??rents aux d??finitions utilis??es par Newton conduirait ?? une r??surgence d'une analyse minutieuse et la preuve formelle dans le 19??me si??cle. Aujourd'hui, les math??maticiens continuent de soutenir entre eux sur preuves assist??e par ordinateur. Depuis grands calculs sont difficiles ?? v??rifier, ces preuves peuvent ne pas ??tre suffisamment rigoureuses. Axiomes de la pens??e traditionnelle ??taient ??v??rit??s ??videntes", mais que la conception est probl??matique. Au niveau formel, un axiome est juste une cha??ne de symboles, qui a une signification intrins??que seulement dans le contexte de l'ensemble des formules derivable d'un syst??me axiomatique. Ce ??tait l'objectif de Le programme de Hilbert pour mettre toutes les math??matiques sur une base axiomatique cabinet, mais selon Th??or??me d'incompl??tude de G??del tous les (suffisamment puissant) syst??me axiomatique a ind??cidables formules; et ainsi une finale axiomatisation des math??matiques est impossible. N??anmoins math??matiques est souvent imagin?? pour ??tre (autant que son contenu formel) rien que la th??orie des ensembles dans certains axiomatisation, dans le sens que tout ??nonc?? math??matique ou de preuve pourraient ??tre jet??s dans des formules dans la th??orie des ensembles.
Les math??matiques comme la science

Carl Friedrich Gauss appel?? math??matiques comme "la reine des sciences??. Dans l'original latin Regina Scientiarum, ainsi que dans allemand K??nigin der Wissenschaften, le mot correspondant ?? des moyens scientifiques (domaine de) la connaissance. En effet, ce est aussi le sens original en anglais, et il ne fait aucun doute que les math??matiques est en ce sens une science. La sp??cialisation restreindre le sens ?? la science naturelle est de date plus tard. Si l'on consid??re la science comme strictement sur le monde physique, puis les math??matiques, ou au moins math??matiques pures, ne est pas une science. Albert Einstein a d??clar?? que ??dans la mesure o?? les lois des math??matiques se r??f??rent ?? la r??alit??, ils ne sont pas certains;. et dans la mesure o?? elles sont certaines, elles ne se r??f??rent pas ?? la r??alit??"
Beaucoup de philosophes croient que les math??matiques ne est pas exp??rimentalement falsifiable, et donc pas une science, selon la d??finition de Karl Popper . Cependant, dans les ann??es 1930 un travail important dans la logique math??matique a montr?? que les math??matiques ne peuvent pas ??tre r??duits ?? la logique, et Karl Popper a conclu que ??la plupart des th??ories math??matiques sont, comme celles de la physique et de la biologie, hypoth??tico-d??ductive: math??matiques pures se av??re donc ??tre beaucoup plus proche aux sciences naturelles dont hypoth??ses sont conjectures, qu'il ne semblait m??me r??cemment ". D'autres penseurs, notamment Imre Lakatos, ont appliqu?? une version de falsificationisme se math??matiques.
Un autre point de vue, ce est que certains domaines scientifiques (telles que physique th??orique) sont les math??matiques avec axiomes qui sont destin??s ?? correspondre ?? la r??alit??. En fait, le physicien th??orique, JM Ziman, a propos?? que la science est de notori??t?? publique et comprend donc les math??matiques. Dans tous les cas, les math??matiques part beaucoup en commun avec de nombreux domaines des sciences physiques, notamment l'exploration des cons??quences logiques d'hypoth??ses. Intuition et exp??rimentation jouent ??galement un r??le dans la formulation de conjectures en math??matiques et les sciences (autres). Math??matiques exp??rimentale continue de cro??tre en importance au sein des math??matiques et le calcul et la simulation jouent un r??le croissant dans les deux les sciences et les math??matiques, l'affaiblissement de l'opposition que les math??matiques ne utilisent pas le m??thode scientifique. Dans son livre 2002 A New Kind of Science, Stephen Wolfram fait valoir que les math??matiques de calcul m??rite d'??tre explor??e empiriquement comme un domaine scientifique ?? part enti??re.
Les opinions des math??maticiens sur cette question sont vari??es. Beaucoup de math??maticiens estiment que d'appeler leur r??gion une science est de minimiser l'importance de son c??t?? esth??tique, et son histoire dans le traditionnel sept arts lib??raux; d'autres estiment que d'ignorer sa connexion aux sciences est de fermer les yeux sur le fait que l'interface entre les math??matiques et ses applications dans les sciences et l'ing??nierie a conduit beaucoup de d??veloppement en math??matiques. Une fa??on cette diff??rence de point de vue se joue est dans le d??bat philosophique de savoir si les math??matiques est cr???? (comme dans l'art) ou d??couvert (comme dans la science). Il est fr??quent de voir des universit??s divis??s en sections qui comprennent une division de sciences et des math??matiques, ce qui indique que les domaines sont consid??r??s comme ??tant des alli??s, mais qu'ils ne co??ncident pas. Dans la pratique, les math??maticiens sont g??n??ralement regroup??s avec des scientifiques au niveau brut, mais s??par??s ?? des niveaux plus fins. Ce est l'une des nombreuses questions examin??es dans le philosophie des math??matiques.
R??compenses math??matiques sont g??n??ralement s??par??s des leurs ??quivalents dans la science. Le prix le plus prestigieux en math??matiques est le M??daille Fields, cr???? en 1936 et d??cern?? tous maintenant quatre ann??es. Il est souvent consid??r??, ?? tort, l'??quivalent de la science de Prix Nobel. Le Prix Wolf de math??matiques, institu?? en 1979, reconna??t les r??alisations de vie, et un autre important prix international, le Prix Abel, a ??t?? introduit en 2003. Ceux-ci sont attribu??s pour un corps particulier de travail, qui peut ??tre l'innovation, ou la r??solution d'un probl??me en suspens dans un champ mis en place. Une fameuse liste de 23 ces probl??mes ouverts, appel??e " Probl??mes de Hilbert ??, ont ??t?? compil??es en 1900 par le math??maticien allemand David Hilbert . Cette liste a r??alis?? une grande c??l??brit?? parmi les math??maticiens, et au moins neuf des probl??mes ont ??t?? r??solus. Une nouvelle liste de sept probl??mes importants, l'intitul?? " Probl??mes du prix du mill??naire ", a ??t?? publi?? en 2000. Solution de chacun de ces probl??mes porte une r??compense de 1 million de dollars et un seul (la Hypoth??se de Riemann) est dupliqu?? dans Probl??mes de Hilbert.
Domaines des math??matiques

Comme indiqu?? plus haut, les principales disciplines dans les math??matiques premier d??coulaient de la n??cessit?? de faire des calculs dans le commerce, de comprendre les relations entre les nombres, pour mesurer la terre, et de pr??dire astronomiques ??v??nements. Ces quatre besoins peuvent ??tre plus ou moins li??e ?? la large subdivision des math??matiques dans l'??tude de la quantit??, de la structure, de l'espace, et de changer (ce est ?? dire, l'arithm??tique , l'alg??bre , la g??om??trie et l'analyse ). En plus de ces principales pr??occupations, il ya aussi des subdivisions d??di?? ?? l'exploration des liens du c??ur des math??matiques ?? d'autres champs: ?? logique, th??orie des ensembles ( fondations), aux math??matiques empiriques des diff??rentes sciences ( math??matiques appliqu??es ), et plus r??cemment ?? l'??tude rigoureuse de incertitude.
Quantit??
L'??tude de la quantit?? commence par un nombre premier, les familiers des nombres naturels et des nombres entiers ("nombres entiers") et les op??rations arithm??tiques sur eux, qui sont caract??ris??s en arithm??tique . Les propri??t??s les plus profondes de entiers sont ??tudi??s dans la th??orie des nombres , o?? ces r??sultats populaires comme le dernier th??or??me de Fermat . La th??orie des nombres d??tient ??galement deux probl??mes non r??solus largement consid??r??es: la conjecture des nombres premiers jumeaux et la conjecture de Goldbach .
Comme le syst??me de num??ro est d??velopp??, les entiers sont reconnus comme un sous-ensemble des nombres rationnels (?? fractions ??). Ceux-ci, ?? leur tour, sont contenues dans les nombres r??els , qui sont utilis??s pour repr??senter des quantit??s continues. Les nombres r??els sont g??n??ralis??s ?? des nombres complexes . Ce sont les premi??res ??tapes d'une hi??rarchie des num??ros qui se passe ?? inclure quarternions et octonions. Examen des nombres naturels conduit ??galement ?? la nombres transfinis, qui formalisent le concept de comptage ?? l'infini. Un autre domaine d'??tude est de taille, ce qui conduit ?? des nombres cardinaux et ensuite ?? une autre conception de l'infini: la num??ros Aleph, qui permettent une comparaison significative de la taille d'une infinit?? de grands ensembles.
Structure
Beaucoup d'objets math??matiques, comme ensembles de nombres et fonctions , pr??sentent la structure interne. Les propri??t??s structurelles de ces objets sont ??tudi??es dans l'??tude des groupes , bagues, les champs et les autres syst??mes abstraits, qui sont eux-m??mes de tels objets. Ce est le domaine de l'alg??bre abstraite . Un concept important ici est que des vecteurs , g??n??ralis??e ?? espaces vectoriels , et a ??tudi?? ?? l'alg??bre lin??aire . L'??tude des vecteurs combine trois des domaines fondamentaux des math??matiques:. Quantit??, structure, et l'espace calcul vectoriel ??largit le champ en quart domaine fondamental, celui du changement.




La th??orie des nombres Alg??bre abstraite La th??orie des groupes la th??orie de la commande
Espace
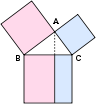
L'??tude de l'espace ??mane de la g??om??trie - en particulier, la g??om??trie euclidienne . trigonom??trie combine espace et num??ros, et englobe la c??l??bre th??or??me de Pythagore . L'??tude moderne de l'espace g??n??ralise ces id??es ?? inclure la g??om??trie de dimension sup??rieure, g??om??tries non-euclidiennes (qui jouent un r??le central dans la relativit?? g??n??rale ) et topologie . Quantit?? et l'espace jouent tous deux un r??le dans la g??om??trie analytique , g??om??trie diff??rentielle , et g??om??trie alg??brique. Dans la g??om??trie diff??rentielle sont les concepts de faisceaux de fibres et le calcul sur les collecteurs . Dans la g??om??trie alg??brique est la description des objets g??om??triques comme des ensembles de solutions de polyn??mes ??quations, combinant les notions de quantit?? et de l'espace, ainsi que l'??tude de groupes topologiques, qui combinent la structure et de l'espace. groupes de Lie sont utilis??es pour ??tudier l'espace, la structure, et le changement. Topologie dans toutes ses nombreuses ramifications peut-??tre la plus grande zone de croissance en math??matiques 20e si??cle, et comprend de longue date Conjecture de Poincar?? et le controvers?? th??or??me des quatre couleurs , dont la preuve que, par ordinateur, n'a jamais ??t?? v??rifi?? par un humain.
Changement
Comprendre et d??crire le changement est un th??me commun dans le sciences naturelles, et le calcul a ??t?? d??velopp?? comme un outil puissant pour faire enqu??te. Fonctions posent ici, comme un concept central d??crivant une quantit?? ??volution. L'??tude rigoureuse des nombres r??els et fonctions r??elles est connu comme analyse r??elle, avec analyse complexe le champ ??quivalent pour les nombres complexes. Le Hypoth??se de Riemann, l'une des questions ouvertes les plus fondamentaux en math??matiques, est tir??e de l'analyse complexe. Analyse fonctionnelle met l'accent sur (g??n??ralement de dimension infinie) des espaces de fonctions. L'une des nombreuses applications de l'analyse fonctionnelle est la m??canique quantique . Beaucoup de probl??mes conduisent naturellement aux relations entre une quantit?? et son taux de variation, et ceux-ci sont ??tudi??s comme des ??quations diff??rentielles . De nombreux ph??nom??nes dans la nature peuvent ??tre d??crits par syst??mes dynamiques; la th??orie du chaos rend pr??cis la fa??on dont beaucoup de ces syst??mes pr??sentent impr??visibles mais toujours comportement d??terministe.
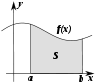 |  |  |  | 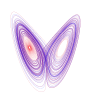 |
| Calcul | Calcul vectoriel | ??quations diff??rentielles | Syst??mes dynamiques | La th??orie du chaos |
Fondations et de la philosophie
Afin de clarifier la fondements des math??matiques, les champs de la logique math??matique et la th??orie des ensembles ont ??t?? ??labor??s, ainsi que la th??orie de la cat??gorie qui est encore en d??veloppement.
La logique math??matique est pr??occup?? par la mise en math??matiques sur un rigide cadre axiomatique, et d'??tudier les r??sultats d'un tel cadre. En tant que tel, il est le foyer de Deuxi??me th??or??me d'incompl??tude de G??del, peut-??tre le r??sultat le plus largement c??l??br?? dans la logique, qui (de mani??re informelle) implique que toute syst??me formel qui contient l'arithm??tique de base, si le son (ce qui signifie que tous les th??or??mes qui peuvent ??tre prouv??es sont vraies), est n??cessairement incompl??te (ce qui signifie qu'il ya de v??ritables th??or??mes qui ne peuvent pas ??tre prouv??s dans ce syst??me). G??del a montr?? comment construire, quelle que soit la collection donn??e d'axiomes la th??orie des nombres, une d??claration formelle dans la logique qui est un nombre th??orique fait vrai, mais qui ne suivent pas de ces axiomes. Par cons??quent pas de syst??me formel est un v??ritable axiomatisation de la th??orie des nombres plein. La logique moderne est divis?? en th??orie r??cursivit??, th??orie des mod??les, et la preuve la th??orie, et est ??troitement li??e ?? th??orique informatique .
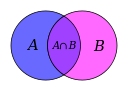
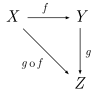
La logique math??matique La th??orie des ensembles La th??orie des cat??gories
Les math??matiques discr??tes
Les math??matiques discr??tes est le nom commun pour les domaines des math??matiques les plus g??n??ralement utiles dans informatique th??orique. Ceci comprend th??orie de la calculabilit??, th??orie de la complexit?? de calcul, et th??orie de l'information. th??orie de la calculabilit?? examine les limites de diff??rents mod??les th??oriques de l'ordinateur, y compris le mod??le le plus puissant connue - la Machine de Turing. th??orie de la complexit?? est l'??tude de tra??abilit?? par ordinateur; certains probl??mes, bien que th??oriquement r??soluble par ordinateur, sont si co??teux en termes de temps ou d'espace qui leur r??solution est susceptible de rester pratiquement impossible, m??me avec l'avance rapide du mat??riel informatique. Enfin, la th??orie de l'information est pr??occup?? par la quantit?? de donn??es pouvant ??tre stock??es sur un support donn??, et donc des concepts tels que compression et entropie.
Comme un domaine relativement nouveau, math??matiques discr??tes a un certain nombre de probl??mes fondamentaux ouverts. Le plus c??l??bre d'entre eux est le " P = NP? "Probl??me, l'un des Probl??mes du prix du mill??naire.


Combinatoire Th??orie du calcul Cryptographie Th??orie des graphes
Math??matiques appliqu??es
Math??matiques appliqu??es consid??re l'utilisation d'outils math??matiques abstraits dans la r??solution de probl??mes concrets dans les sciences , des affaires et d'autres domaines. Un domaine important en math??matiques appliqu??es est des statistiques , qui utilise la th??orie des probabilit??s comme un outil et permet la description, l'analyse et la pr??vision des ph??nom??nes o?? le hasard joue un r??le. La plupart des exp??riences, des enqu??tes et des ??tudes d'observation n??cessitent l'utilisation ??clair??e des statistiques. (Beaucoup de statisticiens, toutefois, ne se consid??rent pas comme des math??maticiens, mais plut??t une partie d'un groupe alli??.) Analyse num??rique enqu??te sur les m??thodes de calcul pour r??soudre efficacement un large ??ventail de probl??mes math??matiques qui sont g??n??ralement trop grand pour la capacit?? num??rique humaine; il comprend l'??tude des erreurs d'arrondi ou d'autres sources d'erreur dans les calculs.

Analyse num??rique 
Optimisation 
Math??matiques financi??res
Id??es re??ues
Math??matiques ne est pas un syst??me ferm?? intellectuelle, dans lequel tout a d??j?? ??t?? ??labor??. Il ne manque pas de probl??mes ouverts. Math??maticiens publier des milliers de documents incorporant de nouvelles d??couvertes en math??matiques chaque mois.
Math??matiques ne est pas num??rologie, il ne est pas la comptabilit?? ; ni est-il limit?? ?? l'arithm??tique .
Pseudo-est une forme d'activit?? comme les math??matiques r??alis??es ?? l'ext??rieur le milieu universitaire, et parfois par les math??maticiens eux-m??mes. Il se compose souvent d'attaques sur des questions d??termin??es c??l??bres, comprenant des correcteurs tentatives faites de mani??re isol??e (ce est-longs documents ne sont pas support??es par la th??orie pr??c??demment publi??e). La relation de math??matiques g??n??ralement admis est similaire ?? celle entre pseudoscience et la vraie science. Les id??es fausses impliqu??s sont normalement bas??s sur:
- incompr??hension des implications de rigueur math??matique;
- les tentatives de contourner les crit??res habituels de la publication de documents math??matiques dans un revue savante apr??s examen par les pairs, souvent dans la croyance que la revue est un parti pris contre l'auteur;
- manque de familiarit?? avec, et donc sous-estimation de la litt??rature existante.
Le cas de Le travail de Kurt Heegner montre que la cr??ation math??matique ne est ni infaillible, ni ne veulent pas admettre l'erreur dans l'??valuation du travail 'amateur'. Et comme l'astronomie , les math??matiques doit beaucoup ?? contributeurs amateurs comme Fermat et Mersenne.
Math??matiques et la r??alit?? physique
Concepts et th??or??mes math??matiques ne doivent pas correspondre ?? quelque chose dans le monde physique. Dans la mesure o?? il existe une correspondance, alors que les math??maticiens et les physiciens peuvent s??lectionner axiomes et postulats qui semblent raisonnables et intuitive, il ne est pas n??cessaire pour les hypoth??ses de base dans un syst??me axiomatique pour ??tre vrai dans un sens empirique ou physique. Ainsi, alors que beaucoup syst??mes d'axiomes sont tir??es de nos perceptions et exp??riences, ils ne sont pas ?? leur charge.
Par exemple, nous pourrions dire que le concept physique de deux pommes peut ??tre pr??cise mod??lis?? par le nombre naturel 2. D'autre part, nous pourrions ??galement dire que les nombres naturels ne sont pas un mod??le pr??cis, car il n'y a pas "unit??" pomme standard et aucune deux pommes sont exactement semblables. L'id??e de la mod??lisation est encore compliqu??e par la possibilit?? de fractions des pommes ou partielles. Ainsi, alors il peut ??tre instructif de visualiser la d??finition axiomatique des nombres naturels comme des collections de pommes, la d??finition m??me ne d??pend pas ni d??riv?? de toutes les entit??s physiques r??elles.
N??anmoins, les math??matiques demeure extr??mement utile pour r??soudre les probl??mes du monde r??el. Ce fait conduit physicien Eugene Wigner d'??crire un article intitul?? " Le d??raisonnable efficacit?? des math??matiques dans les sciences naturelles ".