Th??or??me

Une image math??matique vaut mille mots: le th??or??me de Pythagore .

En la logique math??matique, un th??or??me est un type de objet abstrait, une de jeton qui est un une formule de langage formel qui peut ??tre d??riv??e ?? partir de la r??gles de la syst??me formel qui est appliqu??e ?? la langue formelle; un autre signe de ce qui est une d??claration langage naturel, qui peut ??tre prouv?? sur la base d'hypoth??ses explicitement ??nonc??es ou pr??alablement convenues.

Dans tous les param??tres, une propri??t?? essentielle de th??or??mes, ce est qu'ils peuvent ??tre d??riv??es en utilisant un ensemble fixe de r??gles d'inf??rence et axiomes sans les hypoth??ses suppl??mentaires. Ce ne est pas une question de la s??mantique du langage: l'expression qui r??sulte d'une d??rivation est un cons??quence syntaxique de toutes les expressions qui la pr??c??dent. En math??matiques , la d??rivation d'un th??or??me est souvent interpr??t??e comme une preuve de la v??rit?? de l'expression r??sultante, mais diff??rent syst??mes d??ductifs peuvent donner d'autres interpr??tations, selon les significations des r??gles de d??rivation.

Les preuves de th??or??mes ont deux composantes, appel?? hypoth??ses et la conclusions. La d??monstration d'un th??or??me math??matique est un argument logique d??montrant que les conclusions sont une cons??quence n??cessaire des hypoth??ses, dans le sens que si les hypoth??ses sont vraies alors les conclusions doivent aussi ??tre vrai, sans autres hypoth??ses. Le concept d'un th??or??me est donc fondamentalement d??ductive, contrairement ?? l'id??e d'une scientifique th??orie, qui est empirique.

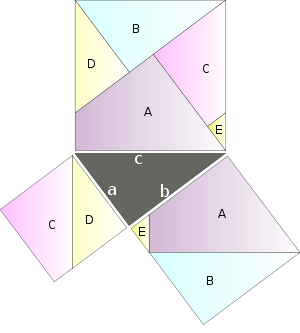
M??me si elles peuvent ??tre ??crites dans un compl??tement forme symbolique, th??or??mes sont souvent exprim??es dans un langage naturel comme l'anglais. La m??me chose est vraie des preuves, qui sont souvent exprim??s comme logiquement organis?? et clairement formul?? arguments informels destin??s ?? d??montrer que la preuve symbolique formelle peut ??tre construit. De tels arguments sont g??n??ralement plus faciles ?? v??rifier que purement symboliques - en effet, de nombreux math??maticiens exprimer une pr??f??rence pour une preuve que non seulement d??montre la validit?? d'un th??or??me, mais explique aussi en quelque sorte pourquoi il est ??videmment vrai. Dans certains cas, une image peut suffire ?? prouver un th??or??me.

Parce th??or??mes sont au c??ur des math??matiques, ils sont ??galement au c??ur de son esth??tique. Th??or??mes sont souvent d??crits comme ??tant ??trivial??, ou ??difficile?? ou ??profond??, ou m??me ??beau??. Ces jugements subjectifs varient non seulement d'une personne ?? personne, mais aussi avec le temps: par exemple, comme une preuve est simplifi??e ou mieux compris, un th??or??me qui ??tait autrefois difficile peut devenir trivial. D'autre part, un th??or??me profonde peut ??tre simplement d??clar??, mais sa d??monstration peut impliquer des connexions surprenantes et subtiles entre les zones disparates de math??matiques. dernier th??or??me de Fermat est un exemple particuli??rement bien connu d'un tel th??or??me.

Notions formelles et informelles

Logiquement la plupart des th??or??mes sont de la forme d'un indicative conditionnelle:. si A, puis B Un tel th??or??me ne affirme pas que B est toujours vrai, mais seulement que B doit ??tre vrai si A est vrai. Dans ce cas, A est appel?? le hypoth??se du th??or??me (?? noter que ??hypoth??se?? ici est quelque chose de tr??s diff??rent d'un conjecture) et B la conclusion. Le th??or??me "Si n est un m??me nombre naturel alors n / 2 est un nombre naturel ??est un exemple typique o?? l'hypoth??se est que n est un nombre pair naturel et la conclusion est que n / 2 est ??galement un nombre naturel.

Afin d'??tre prouv??e, un th??or??me doit ??tre exprim?? sous la forme, une d??claration officielle pr??cise. N??anmoins, th??or??mes sont g??n??ralement exprim??s en langage naturel plut??t que dans une forme compl??tement symbolique, avec l'intention que le lecteur sera en mesure de produire une d??claration officielle de l'informel. En outre, il ya souvent des hypoth??ses qui sont compris dans son contexte, plut??t que dit explicitement.

Il est fr??quent en math??matiques de choisir un certain nombre d'hypoth??ses qui sont suppos??s ??tre vrai dans une th??orie donn??e, puis d??clarent que la th??orie se compose de tous les th??or??mes prouvables utilisant ces hypoth??ses comme hypoth??ses. Dans ce cas, les hypoth??ses qui forment la base fondamentale sont appel??s axiomes ou postulats () de la th??orie. Le domaine des math??matiques appel??s th??orie de la preuve ??tudie les syst??mes d'axiomes formels et les preuves qui peuvent ??tre effectu??es en leur sein.

Un plan carte avec cinq couleurs telles que deux r??gions avec la m??me couleur se rencontrent. Il peut en fait ??tre color??e de cette fa??on avec seulement quatre couleurs. Le th??or??me des quatre couleurs indique que ces colorants sont possibles pour toute carte plane, mais toutes les preuves connu implique une recherche de calcul qui est trop long pour v??rifier ?? la main.

Certains th??or??mes sont "trivial", dans le sens o?? ils suivent des d??finitions, axiomes et autres th??or??mes fa??ons ??videntes et ne contiennent pas de aper??us surprenants. Certains, d'autre part, peut ??tre appel?? ??profonde??: leurs preuves peuvent ??tre longue et difficile, implique domaines des math??matiques superficiellement distincte de la d??claration du th??or??me lui-m??me, ou de montrer des liens surprenants entre zones disparates de math??matiques. Un th??or??me pourrait ??tre simple ?? ??noncer et pourtant ??tre profond. Un excellent exemple est le dernier th??or??me de Fermat , et il ya beaucoup d'autres exemples de th??or??mes encore profondes simples dans la th??orie des nombres et la combinatoire , entre autres domaines.

Il ya d'autres th??or??mes pour lesquels une preuve est connu, mais la preuve ne peuvent pas facilement ??tre ??crites. Les exemples les plus frappants sont les th??or??me de couleur Quatre et de la Conjecture de Kepler. Ces deux th??or??mes ne sont connus pour ??tre vrai en les r??duisant ?? une recherche de calcul qui est ensuite v??rifi??e par un programme informatique. Initialement, de nombreux math??maticiens ne ont pas accept?? cette forme de preuve, mais il est devenu plus largement accept??s au cours des derni??res ann??es. Le math??maticien Doron Zeilberger est m??me all?? jusqu'?? pr??tendre que ce sont probablement les seuls r??sultats non triviaux que les math??maticiens ont jamais prouv??. Beaucoup de th??or??mes math??matiques peuvent ??tre r??duits au calcul plus simple, y compris les identit??s polynomiales, identit??s trigonom??triques et les identit??s hyperg??om??triques.

Relation ?? la preuve

La notion d'un th??or??me est intimement li??e ?? la notion de preuve. En effet, th??or??mes sont remplies avec pr??cision dans le sens o?? ils poss??dent des preuves. Par cons??quent, d'??tablir un ??nonc?? math??matique comme un th??or??me, l'existence d'une ligne de raisonnement des axiomes dans le syst??me (et d'autres, les th??or??mes d??j?? ??tablis) ?? la d??claration donn??e doit ??tre d??montr??e.

Bien que la preuve est n??cessaire pour produire un th??or??me, il ne est g??n??ralement pas consid??r?? comme faisant partie du th??or??me. Et m??me si plus d'une preuve peut ??tre connu pour un seul th??or??me, seule la preuve est n??cessaire pour ??tablir la validit?? du th??or??me. Le th??or??me de Pythagore et le droit de r??ciprocit?? quadratique sont en lice pour le titre du th??or??me le plus grand nombre d'??preuves distinctes.

Th??or??mes de logique

Logique , en particulier dans le domaine de la th??orie de la preuve, estime que les d??clarations th??or??mes (appel??es formules ou ainsi form?? formules) d'un langage formel. Un ensemble de r??gles de d??duction, ??galement appel??es r??gles de transformation ou d'un grammaire formelle, doit ??tre fournie. Ces r??gles de d??duction dire exactement quand une formule peut ??tre d??riv?? d'un ensemble de locaux.

Diff??rents ensembles de r??gles de d??rivation donnent lieu ?? des interpr??tations diff??rentes de ce que cela signifie pour une expression soit un th??or??me. Certaines r??gles de d??rivation et les langues officielles sont destin??s ?? capturer raisonnement math??matique; les exemples les plus courants utilisent logique du premier ordre . Autres syst??mes d??ductifs d??crivent la r????criture de termes, tels que les r??gles de r??duction pour calcul λ.

La d??finition de th??or??mes que les ??l??ments d'un langage formel permet des r??sultats en th??orie de la preuve qui ??tudient la structure de preuves formelles et la structure des formules prouvables. Le r??sultat le plus c??l??bre est Le th??or??me d'incompl??tude de G??del; en repr??sentant th??or??mes sur la th??orie des nombres de base comme des expressions dans un langage formel, puis repr??sentant cette langue au sein de la th??orie des nombres lui-m??me, G??del construit des exemples de d??clarations qui ne sont ni prouvables ni r??futable de axiomatisations de la th??orie des nombres.

Relation avec les th??ories scientifiques

Th??or??mes en math??matiques et th??ories scientifiques sont fondamentalement diff??rents dans leur ??pist??mologie. Une th??orie scientifique ne peut ??tre prouv??e; son attribut cl?? est qu'il est falsifiable, qui est, il fait des pr??dictions sur le monde naturel qui sont testables par exp??riences. Tout d??saccord entre pr??vision et exp??rience d??montre l'inexactitude de la th??orie scientifique, ou au moins de limiter leur exactitude ou leur domaine de validit??. Th??or??mes math??matiques, d'autre part, sont purement d??clarations formelles abstraites: la preuve d'un th??or??me peut pas impliquer exp??riences ou d'autres preuves empiriques de la m??me mani??re telle preuve est utilis?? pour soutenir les th??ories scientifiques.

La conjecture de Syracuse: une fa??on d'illustrer sa complexit?? est d'??tendre l'it??ration des nombres naturels aux nombres complexes. Le r??sultat est une fractale, qui (conform??ment ?? l'universalit??) ressemble ?? l' ensemble de Mandelbrot .

N??anmoins, il ya un certain degr?? de l'empirisme et la collecte de donn??es impliqu??s dans la d??couverte de th??or??mes math??matiques. En ??tablissant un mod??le, parfois avec l'utilisation d'un ordinateur puissant, math??maticiens peuvent avoir une id??e de ce ?? prouver, et dans certains cas m??me un plan pour savoir comment r??gler de faire la preuve. Par exemple, le Collatz Conjecture a ??t?? v??rifi?? pour les valeurs de d??marrage jusqu'?? environ 2,88 ?? 10 ^18. Le Hypoth??se de Riemann a ??t?? v??rifi?? pour les 10000000000000 premiers z??ros de la fonction zeta. Aucune de ces affirmations est consid??r?? ??tre prouv??e.

Ces ??l??ments de preuve ne constitue pas une preuve. Par exemple, le Mertens conjecture est une d??claration au sujet des nombres naturels qui est maintenant connu pour ??tre faux, mais pas contre-explicite (ce est ?? dire, un nombre naturel n pour laquelle la fonction Mertens M (n) est ??gal ou sup??rieur ?? la racine carr??e de n) est connu: tous les num??ros moins de 10 ¹⁴ ont la propri??t?? Mertens, et le plus petit nombre qui ne poss??de pas cette propri??t?? ne est connu pour ??tre inf??rieure ?? la exponentielle de 1,59 ?? 10 ^40, qui est d'environ 10 ?? la puissance 4,3 ?? 10 ^39. Comme le nombre de particules dans l'univers est g??n??ralement consid??r??s comme moins de 10 ?? la puissance 100 (un googol), il n'y a aucun espoir de trouver un contre-exemple explicite recherche exhaustive ?? l'heure actuelle.

Notez que le mot ??th??orie?? existe aussi en math??matiques, pour d??signer un corps d'axiomes math??matiques, les d??finitions et th??or??mes, comme, par exemple, la th??orie des groupes . Il ya aussi des ??th??or??mes?? dans la science, en particulier la physique et de l'ing??nierie, mais ils ont souvent des d??clarations et des preuves dans lequel hypoth??ses physiques et l'intuition jouent un r??le important; les axiomes physiques sur lesquels ces ??th??or??mes?? sont fond??s sont eux-m??mes falsifiables.

Terminologie

Th??or??mes sont souvent indiqu??es par plusieurs autres termes: l'??tiquette ??th??or??me?? r??elle est r??serv?? pour les r??sultats les plus importants, alors que les r??sultats qui sont moins importants, ou distingu??s par d'autres moyens, sont nomm??s par une terminologie diff??rente.

• Un proposition est une d??claration non associ?? ?? tout th??or??me particulier. Ce terme ??voque parfois une d??claration avec une preuve simple.
• Un lemme est un ??pr??-th??or??me", une d??claration qui fait partie de la preuve d'un th??or??me plus grande. La distinction entre les th??or??mes et lemmes est plut??t arbitraire, puisque l'un de math??maticien r??sultat majeur est une autre r??clamation est mineur. Lemme de Gauss et Lemme de Zorn, par exemple, sont assez int??ressant de noter que certains auteurs pr??sentent le lemme nominale sans passer ?? l'utiliser dans la d??monstration d'un th??or??me.
• Un corollaire est une proposition qui suit avec peu ou pas de preuve d'un autre th??or??me ou une d??finition. Ce est, proposition B est un corollaire d'une proposition A si B peut ??tre facilement d??duit de A.
• Une r??clamation est un r??sultat n??cessaire ou ind??pendamment int??ressante qui peut faire partie de la preuve d'une autre instruction. Malgr?? le nom, les r??clamations doivent ??tre prouv??es.

Il ya d'autres termes, moins couramment utilis??s, qui sont classiquement attach??s aux ??tats ??prouv??s, de sorte que certains th??or??mes sont d??sign??s par des noms historiques ou coutumi??res. Pour exemples:

• Identit??, utilis?? pour th??or??mes qui indiquent une ??galit?? entre deux expressions math??matiques. Les exemples incluent l'identit?? d'Euler et Identit?? de Vandermonde.
• R??gle, utilis?? pour certains th??or??mes tels que La r??gle de Bayes et La r??gle de Cramer, qui ??tablissent formules utiles.
• Loi. Des exemples comprennent le loi des grands nombres, le loi des cosinus, et Loi du z??ro un de Kolmogorov.
• Principe. Des exemples comprennent Principe de Harnack, le principe limite sup??rieure moins, et de la classer principe.
• Un Converse est un th??or??me inverse. Par exemple, si un th??or??me affirme que A est une li?? ?? B, ce est r??ciproque ??noncerait que B est li?? ?? A. L'inverse d'un th??or??me ne est pas n??cessairement toujours vrai.

A quelques th??or??mes bien connus ont des noms encore plus idiosyncrasiques. Le division algorithme un th??or??me exprimant le r??sultat de la division dans les nombres naturels et des anneaux plus g??n??raux. Le Banach-Tarski paradoxe est un th??or??me th??orie de la mesure ce est- paradoxale dans la mesure o?? elle contredit intuitions communes sur le volume dans l'espace en trois dimensions.

Une d??claration ?? prouver que l'on croit ??tre vrai est appel?? conjecture (ou parfois une hypoth??se, mais avec un sens diff??rent de celui d??crit ci-dessus). Pour ??tre consid??r?? comme une conjecture, une d??claration doit g??n??ralement ??tre propos?? au public, ?? quel point le nom du promoteur peut ??tre attach?? ?? la conjecture, comme avec la conjecture de Goldbach . Autres conjectures c??l??bres incluent la Collatz conjecture et de la Hypoth??se de Riemann.

Disposition

Un th??or??me et sa preuve sont g??n??ralement dispos??s comme suit:

Th??or??me (nom de la personne qui a prouv?? et ann??e de la d??couverte, la preuve ou de la publication).

D??claration du th??or??me.

Preuve.

Description de la preuve.

La fin de la preuve peut ??tre signal?? par les lettres CQFD sens " quod erat demonstrandum ??ou par l'un des marques de Tombstone "□" ou "∎" qui signifie "Fin de la preuve", introduite par Paul Halmos la suite de leur utilisation dans des articles de magazines.

Le style exact d??pendra de l'auteur ou de la publication. Beaucoup de publications fournissent des instructions ou macros pour la composition dans le style maison.

Il est commun pour un th??or??me d'??tre pr??c??d?? par d??finitions d??crivant le sens exact des termes utilis??s dans le th??or??me. Il est ??galement fr??quent pour un th??or??me ?? ??tre pr??c??d??e d'un certain nombre de propositions ou lemmes qui sont ensuite utilis??es dans la preuve. Cependant, lemmes sont parfois int??gr??s dans la d??monstration d'un th??or??me, soit avec des preuves imbriqu??s, ou avec leurs preuves pr??sent??s apr??s la d??monstration du th??or??me.

Corollaires ?? un th??or??me sont soit pr??sent??es entre le th??or??me et la preuve, ou directement apr??s la preuve. Parfois corollaires ont des preuves de leur propre qui expliquent pourquoi ils suivent du th??or??me.

Traditions

Il a ??t?? estim?? que plus d'un quart de million th??or??mes sont prouv??s chaque ann??e.

Le bien-connue aphorisme, "Un math??maticien est un dispositif pour transformer le caf?? en th??or??mes", est probablement due ?? Alfr??d R??nyi, m??me si elle est souvent attribu??e ?? un coll??gue de R??nyi Paul Erdős (et R??nyi peuvent avoir pens?? Erdős), qui ??tait c??l??bre pour les nombreux th??or??mes qu'il produit, le nombre de ses collaborations, et sa consommation de caf??.

Le classification des groupes simples finis est consid??r?? par certains comme la plus longue d??monstration d'un th??or??me; il comprend des dizaines de milliers de pages de 500 articles de revues par certains auteurs 100. Ces documents sont ainsi cens??s donner une preuve compl??te, et il ya plusieurs projets en cours pour raccourcir et simplifier cette preuve.

Chercher th??or??me dans Wiktionary, le dictionnaire libre.