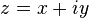Ensemble de Mandelbrot
Renseignements g??n??raux
SOS Enfants a essay?? de rendre le contenu plus accessible Wikipedia par cette s??lection des ??coles. Les enfants SOS est le plus grand don de charit?? du monde enfants orphelins et abandonn??s la chance de la vie familiale.

L'ensemble de Mandelbrot est un ensemble de points dans le plan complexe , le limite forme une fractale . Math??matiquement, l'ensemble de Mandelbrot peut ??tre d??finie comme l'ensemble des -values c complexes pour lesquels la orbite de 0 dans it??ration de la complexe quadratique polyn??me x n + 1 = x 2 n + C reste d??limit??e.
Par exemple. c = 1 donne la s??quence 0, 1, 2, 5, 26 ... ce qui conduit ?? l'infini. Comme cette s??quence ne est pas born??, 1 ne est pas un ??l??ment de l'ensemble de Mandelbrot.
D'un autre c??t??, c = i donne la s??quence 0, i, (-1 + i), -i (-1 + i), ... -i qui est d??limit??e, et si elle appartient ?? l'ensemble de Mandelbrot.
Quand elle est calcul??e et repr??sent??e graphiquement sur le plan complexe, l'ensemble de Mandelbrot est consid??r?? comme ayant une limite ??labor??e, ce qui ne simplifie pas ?? ne importe quel grossissement donn??. Ce qualifie la fronti??re comme une fractale.
L'ensemble de Mandelbrot est devenu populaires en dehors des math??matiques ?? la fois pour son attrait esth??tique et pour ??tre une structure complexe r??sultant d'une d??finition simple. Beno??t Mandelbrot et d'autres ont travaill?? dur pour communiquer domaine des math??matiques au public.
Histoire
L'ensemble de Mandelbrot a sa place dans dynamiques complexes, un premier champ d'une enqu??te par les math??maticiens fran??ais Pierre Fatou et Gaston Julia au d??but du 20??me si??cle. Les premi??res photos de celui-ci ont ??t?? ??tablis en 1978 par Robert et Peter Brooks Matelski dans le cadre d'une ??tude de Groupes kleiniennes.
Mandelbrot a ??tudi?? l'espace des param??tres de polyn??mes quadratiques dans un article paru en 1980. L'??tude math??matique de l'ensemble de Mandelbrot vraiment commenc?? avec le travail par les math??maticiens Adrien Douady et John H. Hubbard, qui a ??tabli plusieurs de ses propri??t??s fondamentales et nomm?? en l'honneur de l'ensemble de Mandelbrot.
Les math??maticiens Heinz-Otto et Peitgen Peter Richter est devenu bien connu pour la promotion de l'ensemble de photographies sur papier glac??, des livres, et une galerie de tourisme.
L'article de couverture du Ao??t 1985 Scientific American en vedette une image cr????e par Mandelbrot, Peitgen, et Hubbard.
Le travail de Douady et Hubbard a co??ncid?? avec une forte augmentation de l'int??r??t pour la dynamique complexes et math??matiques abstraites, et l'??tude de l'ensemble de Mandelbrot a ??t?? une pi??ce ma??tresse de ce champ depuis. Une liste exhaustive de tous les math??maticiens qui ont contribu?? ?? la compr??hension de cet ensemble depuis, ce est au-del?? du champ d'application de cet article, mais une telle liste inclurait notamment Mikhail Lyubich, Curt McMullen, John Milnor, Mitsuhiro Shishikura, et Jean-Christophe Yoccoz.
D??finition formelle
L'ensemble de Mandelbrot  est d??finie par une famille de polyn??mes quadratique complexe
est d??finie par une famille de polyn??mes quadratique complexe
donn?? par
 ,
,
o??  est un param??tre complexe. Pour chaque
est un param??tre complexe. Pour chaque  , On consid??re le comportement de la s??quence
, On consid??re le comportement de la s??quence 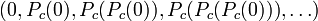 obtenu par it??ration
obtenu par it??ration 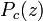 ?? partir de point critique
?? partir de point critique  , Qui soit se ??chappe ?? l'infini ou reste dans un disque de certains rayon fini. L'ensemble de Mandelbrot est d??fini comme l'ensemble de tous les points
, Qui soit se ??chappe ?? l'infini ou reste dans un disque de certains rayon fini. L'ensemble de Mandelbrot est d??fini comme l'ensemble de tous les points  de telle sorte que la s??quence ci-dessus ne se ??chappe pas ?? l'infini.
de telle sorte que la s??quence ci-dessus ne se ??chappe pas ?? l'infini.

Plus formellement, si  d??signe le n-i??me it??ration de
d??signe le n-i??me it??ration de 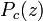 (C.
(C. 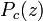 compos?? avec lui-m??me n fois), l'ensemble de Mandelbrot est le sous-ensemble du plan complexe donn??e par
compos?? avec lui-m??me n fois), l'ensemble de Mandelbrot est le sous-ensemble du plan complexe donn??e par
Math??matiquement, l'ensemble de Mandelbrot est juste un un ensemble de nombres complexes. Un nombre complexe donn??  soit appartient ??
soit appartient ??  ou il ne le fait pas. Une image de l'ensemble de Mandelbrot peut ??tre faite par la coloration tous les points
ou il ne le fait pas. Une image de l'ensemble de Mandelbrot peut ??tre faite par la coloration tous les points  qui appartiennent ??
qui appartiennent ??  noir, et tous les autres points blanc. Les photos les plus color??s habituellement vus sont g??n??r??s par des points de colorants ne sont pas dans l'ensemble selon la fa??on dont rapidement ou lentement la s??quence
noir, et tous les autres points blanc. Les photos les plus color??s habituellement vus sont g??n??r??s par des points de colorants ne sont pas dans l'ensemble selon la fa??on dont rapidement ou lentement la s??quence  diverge ?? l'infini. Voir la section sur les dessins informatiques ci-dessous pour plus de d??tails.
diverge ?? l'infini. Voir la section sur les dessins informatiques ci-dessous pour plus de d??tails.
L'ensemble de Mandelbrot peut ??galement ??tre d??finie comme ??tant la connexit?? locus de la famille des polyn??mes 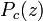 . Autrement dit, ce est le sous-ensemble du plan complexe ces param??tres consistant en
. Autrement dit, ce est le sous-ensemble du plan complexe ces param??tres consistant en  pour lesquels le Ensemble de Julia de
pour lesquels le Ensemble de Julia de  est reli??.
est reli??.
Propri??t??s de base
L'ensemble de Mandelbrot est un ensemble compact , contenue dans le disque ferm?? de rayon 2 autour de l'origine. En fait, un point  appartient ?? l'ensemble de Mandelbrot si et seulement si
appartient ?? l'ensemble de Mandelbrot si et seulement si 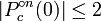 pour tous
pour tous 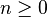 . En d'autres termes, si la valeur absolue de
. En d'autres termes, si la valeur absolue de 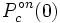 devient de plus en plus grand que 2, la s??quence sera ??chapper ?? l'infini.
devient de plus en plus grand que 2, la s??quence sera ??chapper ?? l'infini.

L' intersection de  avec l'axe r??el est pr??cis??ment l'intervalle
avec l'axe r??el est pr??cis??ment l'intervalle ![[-2, 0,25] \,](../../images/214/21445.png) . Les param??tres le long de cet intervalle peuvent ??tre mis en one-to-one correspondance avec ceux de la vraie famille logistique,
. Les param??tres le long de cet intervalle peuvent ??tre mis en one-to-one correspondance avec ceux de la vraie famille logistique,
La correspondance est donn??e par
En fait, ce qui donne une correspondance entre l'ensemble de l'espace des param??tres de la famille de logistique et que l'ensemble de Mandelbrot.
La superficie de l'ensemble de Mandelbrot est estim?? ?? 1,506 ?? 0,000 591 77 000 08.
Douady et Hubbard ont montr?? que l'ensemble de Mandelbrot est reli??. En fait, ils ont construit un explicite conforme isomorphisme entre le compl??ment de l'ensemble de Mandelbrot et le compl??ment de la disque de l'unit?? de fermeture. Mandelbrot avait initialement suppos?? que l'ensemble de Mandelbrot est d??branch??. Cette conjecture a ??t?? bas??e sur des images informatiques g??n??r??s par les programmes qui sont incapables de d??tecter les minces filaments reliant les diff??rentes parties du  . Apr??s d'autres exp??riences, il a r??vis?? sa conjecture, d??cidant que
. Apr??s d'autres exp??riences, il a r??vis?? sa conjecture, d??cidant que  doit ??tre connect??.
doit ??tre connect??.
La formule pour la dynamique uniformisation du compl??ment de l'ensemble de Mandelbrot, d??coulant de la preuve de Douady et Hubbard de la connexit?? des  , Donne lieu ?? rayons externes de l'ensemble de Mandelbrot. Ces rayons peuvent ??tre utilis??s pour ??tudier l'ensemble de Mandelbrot en termes combinatoires et forment l'??pine dorsale de la Parapuzzle Yoccoz.
, Donne lieu ?? rayons externes de l'ensemble de Mandelbrot. Ces rayons peuvent ??tre utilis??s pour ??tudier l'ensemble de Mandelbrot en termes combinatoires et forment l'??pine dorsale de la Parapuzzle Yoccoz.
Le fronti??re de l'ensemble de Mandelbrot est exactement le bifurcation locus de la famille quadratique; ce est l'ensemble de param??tres  pour lesquels la dynamique change brusquement sous de petites modifications de
pour lesquels la dynamique change brusquement sous de petites modifications de 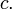 Il peut ??tre construit comme un ensemble d'une s??quence de fin de course courbes alg??briques d'avion, les courbes de Mandelbrot, du type g??n??ral connu sous le nom lemniscates polynomiale. Les courbes de Mandelbrot sont d??finies par la mise en p 0 = z, p n = p n-1 2 + z, puis l'interpr??tation de l'ensemble des points | p n (z) | = 1 dans le plan complexe comme une courbe dans le r??el cart??sien plan de degr?? 2 n + 1 en x et y.
Il peut ??tre construit comme un ensemble d'une s??quence de fin de course courbes alg??briques d'avion, les courbes de Mandelbrot, du type g??n??ral connu sous le nom lemniscates polynomiale. Les courbes de Mandelbrot sont d??finies par la mise en p 0 = z, p n = p n-1 2 + z, puis l'interpr??tation de l'ensemble des points | p n (z) | = 1 dans le plan complexe comme une courbe dans le r??el cart??sien plan de degr?? 2 n + 1 en x et y.
Autres propri??t??s
Les principaux ampoules cardio??de et p??riode

En regardant une image de l'ensemble de Mandelbrot, on remarque imm??diatement le grande r??gion en forme de cardio??de dans le centre. Cette cardio??de principal est la r??gion de param??tres  pour lequel
pour lequel  a un attirer point fixe. Il se compose de tous les param??tres de la forme
a un attirer point fixe. Il se compose de tous les param??tres de la forme
pour certains  dans le ouverte disque unit??.
dans le ouverte disque unit??.
Pour la gauche de la cardio??de principale, attach?? ?? elle au point  Une ampoule de forme circulaire est visible. Cette ampoule est constitu??e de ces param??tres
Une ampoule de forme circulaire est visible. Cette ampoule est constitu??e de ces param??tres  pour lequel
pour lequel  a un attirer cycle de la p??riode 2. Cet ensemble de param??tres est un cercle r??elle, ?? savoir que de rayon autour de 1/4 -1.
a un attirer cycle de la p??riode 2. Cet ensemble de param??tres est un cercle r??elle, ?? savoir que de rayon autour de 1/4 -1.
Il ya une infinit?? de nombreux autres ampoules tangente ?? la cardio??de principale: pour chaque nombre rationnel 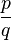 , Avec p et q premiers entre eux, il existe une telle ampoule qui est tangente au param??tre
, Avec p et q premiers entre eux, il existe une telle ampoule qui est tangente au param??tre

Cette ampoule est appel?? le 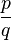 -bulb de l'ensemble de Mandelbrot. Il se compose de param??tres qui ont une p??riode de cycle attractif
-bulb de l'ensemble de Mandelbrot. Il se compose de param??tres qui ont une p??riode de cycle attractif 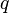 et le nombre de rotation combinatoire
et le nombre de rotation combinatoire 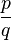 . Plus pr??cis??ment, la
. Plus pr??cis??ment, la 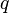 p??riodique Fatou composants contenant le cycle attirer tout contact en un point commun (commun??ment appel?? le
p??riodique Fatou composants contenant le cycle attirer tout contact en un point commun (commun??ment appel?? le  Point -fixed). Si nous appelons ces composants
Point -fixed). Si nous appelons ces composants 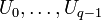 dans une orientation anti-horaire, puis
dans une orientation anti-horaire, puis  Cartes du composant
Cartes du composant  au composant
au composant  .
.

Le changement de comportement se produisant ??  qui est connu comme un bifurcation: le point fixe "entre en collision avec un?? Attirer q -cycle p??riode de r??pulsion. Comme nous passons par le param??tre de bifurcation dans le
qui est connu comme un bifurcation: le point fixe "entre en collision avec un?? Attirer q -cycle p??riode de r??pulsion. Comme nous passons par le param??tre de bifurcation dans le 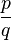 -bulb, le point fixe attirer se transforme en un point fixe r??pulsif (la
-bulb, le point fixe attirer se transforme en un point fixe r??pulsif (la  Point -fixed), et la p??riode q -cycle devient attirant.
Point -fixed), et la p??riode q -cycle devient attirant.
Composantes hyperboliques
Toutes les ampoules que nous avons rencontr??s dans la section pr??c??dente ??taient composants int??rieurs de l'ensemble de Mandelbrot dans lequel les cartes 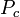 avoir un cycle p??riodique attirer. Ces composants sont appel??s composantes hyperboliques.
avoir un cycle p??riodique attirer. Ces composants sont appel??s composantes hyperboliques.
On suppose que ce sont les seules r??gions de l'int??rieur de  . Ce probl??me, connu sous le nom de densit?? hyperbolicit??, peut-??tre le probl??me ouvert le plus important dans le domaine de la dynamique complexe. Composants non-hyperboliques hypoth??tiques de l'ensemble de Mandelbrot sont souvent d??sign??s comme des composants "queer".
. Ce probl??me, connu sous le nom de densit?? hyperbolicit??, peut-??tre le probl??me ouvert le plus important dans le domaine de la dynamique complexe. Composants non-hyperboliques hypoth??tiques de l'ensemble de Mandelbrot sont souvent d??sign??s comme des composants "queer".
Pour les vrais polyn??mes quadratiques, cette question a ??t?? r??pondu positivement dans les ann??es 1990 de fa??on ind??pendante par Lyubich et en Graczyk et Świątek. (Notez que les composantes hyperboliques coupant l'axe r??els correspondent exactement aux fen??tres p??riodiques dans le Sch??ma Feigenbaum. Donc, ce r??sultat indique que ces fen??tres existent pr??s de chaque param??tre dans le sch??ma.)
Non chaque composante hyperbolique peut ??tre atteint par une s??quence de bifurcations directs de la cardio??de principal de l'ensemble de Mandelbrot. Cependant, un tel composant peut ??tre atteint par une s??quence de bifurcations directs de la cardio??de principal d'une petite copie Mandelbrot (voir ci-dessous).
Connectivit?? locale
On suppose que l'ensemble de Mandelbrot est connect?? localement. Cette fameuse conjecture est connu comme MLC (pour Mandelbrot connect??s localement). Par le travail de Adrien Douady et John H. Hubbard, cette conjecture se traduirait par un mod??le simple abstrait "disque pinc???? de l'ensemble de Mandelbrot. En particulier, cela impliquerait la conjecture de hyperbolicit?? important mentionn?? ci-dessus.
Le c??l??bre ouvrage de Jean-Christophe Yoccoz ??tabli connectivit?? locale de l'ensemble de Mandelbrot ?? tous fini-renormalisable param??tres; ce est, grosso modo celles qui sont contenues seulement dans un nombre fini de petites copies de Mandelbrot. Depuis lors, la connectivit?? locale a ??t?? prouv?? dans de nombreux autres points de  , Mais la conjecture compl??te est toujours ouverte.
, Mais la conjecture compl??te est toujours ouverte.
Auto-similarit??

 .
. 
L'ensemble de Mandelbrot est auto-similaire ?? la loupe dans les quartiers de la Les points Misiurewicz. Il est ??galement conjectur?? ??tre auto-similaire autour g??n??ralis??e Feigenbaum des points (par exemple -1,401155 ou -.1528 + 1.0397i), dans le sens d'une convergence vers un ensemble de limite.

L'ensemble de Mandelbrot en g??n??ral ne est pas strictement auto-similaire mais il est quasi-auto-similaire, comme de petites versions l??g??rement diff??rentes de lui-m??me peut ??tre trouv?? ?? arbitrairement petites ??chelles.
Les petites copies de l'ensemble de Mandelbrot sont tous l??g??rement diff??rents, surtout ?? cause des minces filets qui les relient au corps principal de l'ensemble.
D'autres r??sultats
Le Hausdorff dimension de la fronti??re de l'ensemble de Mandelbrot est ??gal ?? 2 tel que d??termin?? par la suite de Mitsuhiro Shishikura. On ne sait pas si la fronti??re de l'ensemble de Mandelbrot a plane positif Mesure de Lebesgue.
Dans le Mod??le Blum-Shub-Smale de calcul r??el, l'ensemble de Mandelbrot ne est pas calculable, mais son compl??ment est r??cursivement ??num??rable. Cependant, de nombreux objets simples (par exemple, le graphe de exponentiation) ne sont ??galement pas calculable dans le mod??le BSS. ?? l'heure actuelle, on ignore si l'ensemble de Mandelbrot est calculable dans les mod??les de calcul r??el bas??e sur analyse r??cursive, qui correspondent plus ??troitement ?? la notion intuitive de "comploter l'ensemble par un ordinateur." Hertling a montr?? que l'ensemble de Mandelbrot est calculable dans ce mod??le si la conjecture de hyperbolicit?? est vrai.
Relations avec les ensembles de Julia

En cons??quence de la d??finition de l'ensemble de Mandelbrot, il existe une correspondance ??troite entre la g??om??trie de l'ensemble de Mandelbrot ?? un moment donn?? et la structure du correspondant Ensemble de Julia.
Ce principe est exploit??e dans les r??sultats quasi-totalit?? profondes sur l'ensemble de Mandelbrot. Par exemple, Shishikura prouve que, pour un ensemble dense de param??tres dans la limite de l'ensemble de Mandelbrot, l'ensemble de Julia a Dimension de Hausdorff deux, et puis transf??re ces informations au plan de param??tre. De m??me, Yoccoz prouve d'abord la connectivit?? locale des ensembles de Julia, avant d'??tablir pour l'ensemble de Mandelbrot les param??tres correspondants. Adrien Douady Phrases ce principe
Plough dans le plan dynamique, et la r??colte dans l'espace des param??tres.
G??om??trie

Rappelons que, pour chaque nombre rationnel 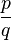 O??
O?? 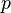 et
et 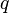 sont relativement premiers, il ya une composante hyperbolique de la p??riode
sont relativement premiers, il ya une composante hyperbolique de la p??riode 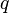 bifurquant ?? partir de la cardio??de principale. La partie de l'ensemble de Mandelbrot reli?? ?? la cardio??de principal ?? ce point de bifurcation est appel?? le p / q-membre. exp??riences informatiques sugg??rent que le diam??tre de la branche tend vers z??ro comme
bifurquant ?? partir de la cardio??de principale. La partie de l'ensemble de Mandelbrot reli?? ?? la cardio??de principal ?? ce point de bifurcation est appel?? le p / q-membre. exp??riences informatiques sugg??rent que le diam??tre de la branche tend vers z??ro comme 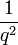 . La meilleure estimation actuelle connue est la c??l??bre Yoccoz l'in??galit??, qui stipule que la taille tend vers z??ro comme
. La meilleure estimation actuelle connue est la c??l??bre Yoccoz l'in??galit??, qui stipule que la taille tend vers z??ro comme  .
.
Une p??riode 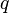 -limb auront
-limb auront 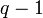 ??Antennes?? en haut de sa branche. On peut donc d??terminer la p??riode d'une ampoule donn??e en comptant ces antennes.
??Antennes?? en haut de sa branche. On peut donc d??terminer la p??riode d'une ampoule donn??e en comptant ces antennes.
G??n??ralisations

Parfois, le locus de la connectivit?? des familles autres que la famille quadratique est ??galement d??sign?? sous le nom de Mandelbrot de ces familles.
Le locus de connexit?? des familles de polyn??mes unicritical  pour
pour  sont souvent appel??s ensembles Multibrot.
sont souvent appel??s ensembles Multibrot.

Pour les familles g??n??rales de fonctions holomorphes, la limite de l'ensemble de Mandelbrot se g??n??ralise au bifurcation locus, qui est un objet naturel d'??tudier m??me lorsque le lieu de connexit?? ne est pas utile.
Il est ??galement possible d'envisager des structures similaires dans l'??tude des mappages non analytiques. D'un int??r??t particulier est le tricorne, le lieu de la connectivit?? de la famille anti-holomorphe
Le tricorne (parfois aussi appel?? l'ensemble Mandelbar) a ??t?? rencontr??e par Milnor dans son ??tude de tranches de param??tres de polyn??mes r??els cubes. Il ne est pas connect?? localement. Cette propri??t?? est h??rit??e par le locus de connexit?? des polyn??mes r??els cubes.
dessins informatiques


Algorithmes:
- ??chapper algorithme de temps
- Version bool??enne (attire M-set et son ext??rieur en utilisant deux couleurs) = algorithme Mandelbrot
- discret (entier) version = level set m??thode (LSM / M); attire ensemble de Mandelbrot et de bandes de couleur dans son ext??rieur
- version continue
- courbes de niveau version = attire lemniscates d'ensemble de Mandelbrot = limites d'ensembles de niveau
- la d??composition de l'ext??rieur des ensemble de Mandelbrot
- potentiel complexe
- Hubbard-Douady (r??el) potentiel des ensemble de Mandelbrot (CPM / M) - partie radiale du potentiel complexe
- angle externe de Mandelbrot set - partie angulaire du potentiel complexe
- abstraite M-set
- Distance m??thode d'estimation pour ensemble de Mandelbrot
- estimation de distance ext??rieur = algorithme Milnor (DEM / M)
- int??rieur estimation de la distance
- algorithme utilis?? pour explorer l'int??rieur d'ensemble de Mandelbrot
- p??riode de composantes hyperboliques
- multiplicateur de orbite p??riodique (rayons internes (angle) et le rayon intenal)
- bof61 et bof60
Chaque algorithme peut ??tre mis en oeuvre s??quentielle ou version parall??le. La sym??trie miroir peut ??tre utilis?? pour des calculs d'acc??l??ration .
| Wikibooks a un livre sur le th??me de: Fractales |
??chapper algorithme de temps
L'algorithme simple pour g??n??rer une repr??sentation de l'ensemble de Mandelbrot est connu comme l'algorithme "??chapper au temps". Un calcul r??p??tition est effectu??e pour chaque x, point dans la zone de la parcelle y et bas??e sur le comportement de ce calcul, une couleur est choisie pour ce pixel.
X et Y emplacement de chaque point sont utilis??s comme valeurs de d??part dans une r??p??tition, ou it??ration calcul (d??crit en d??tail ci-dessous). Le r??sultat de chaque it??ration est utilis?? comme valeur de d??part pour l'autre. Les valeurs sont v??rifi??s lors de chaque it??ration pour voir si elles ont atteint un ????chapper?? un ??tat critique. Si cette condition est atteinte, le calcul est ?? l'arr??t, le pixel est trac??, et les prochaines x, y point est examin??. Pour certaines valeurs de d??part, l'??vasion se produit rapidement, apr??s seulement un petit nombre d'it??rations. Pour les autres valeurs de d??part, il peut prendre des centaines ou des milliers d'it??rations de se ??chapper. Pour les valeurs au sein de l'ensemble de Mandelbrot, l'??vasion ne se produira jamais. Le programmeur ou l'utilisateur doit choisir combien it??ration, ou ??profondeur??, ils souhaitent examiner. Plus le nombre maximum d'it??rations, plus de d??tails et la subtilit?? ??merger dans l'image finale, mais le temps que cela prendra pour calculer l'image.
La couleur de chaque point repr??sente la fa??on dont rapidement les valeurs ont atteint le point de fuite. Souvent noir est utilis?? pour afficher les valeurs qui ??chouent ?? se ??chapper avant la limite d'it??ration, et les couleurs vives sont progressivement utilis??s pour les points qui se ??chappent. Ceci donne une repr??sentation visuelle du nombre de cycles ont ??t?? n??cessaires avant d'atteindre l'??tat d'??vacuation.
Pour les programmeurs
La d??finition de l'ensemble de Mandelbrot, avec ses propri??t??s de base, sugg??re un algorithme simple pour dessiner une image de l'ensemble de Mandelbrot. La r??gion du plan complexe nous envisageons est divis?? en un certain nombre de pixels. Pour colorer un tel pixel, laissez-  le point m??dian de ce pixel. Nous parcourons maintenant la valeur critique
le point m??dian de ce pixel. Nous parcourons maintenant la valeur critique  sous
sous 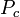 , En v??rifiant ?? chaque ??tape si le point de l'orbite a module plus grand que deux.
, En v??rifiant ?? chaque ??tape si le point de l'orbite a module plus grand que deux.
Si tel est le cas, on sait que la milieu ne appartient pas ?? l'ensemble de Mandelbrot, et nous colorer notre pixel. (Soit on colorie en blanc pour obtenir l'image math??matique simple ou de la couleur en fonction du nombre d'it??rations utilis??es pour obtenir les images color??es bien connus). Sinon, nous continuons it??ration pendant un certain (grand, mais fixe) nombre d'??tapes, apr??s quoi nous d??cidons que notre param??tre est ??probablement?? dans l'ensemble de Mandelbrot, ou au moins tr??s proche de lui, et la couleur du pixel noir.
En pseudo, cet algorithme ressemblerait ?? ce qui suit.
Pour chaque pixel de l'??cran faire: {x = x0 = x coordonn??e du pixel y = y0 = y coordonn??e du pixel it??ration = 0 max_iteration = 1000 tout (x * x + y * y <= (2 * 2 ) et l'it??ration <max_iteration) {x = xtemp * x - y * y + x0 y = 2 * x * y + x = y0 xtemp it??ration it??ration = + 1} if (it??ration == max_iteration) puis color = autre couleur noire = parcelle d'it??ration (x0, y0, couleur)} o??, concernant le pseudo-code ??  et
et 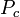 :
:
et si, comme on peut le voir dans le pseudo-code dans le calcul de x et y:
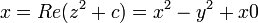 et y =
et y = 
Pour obtenir des images color??es de l'ensemble, l'affectation d'une couleur ?? chaque valeur du nombre d'it??rations ex??cut??es peut ??tre fait en utilisant une d'une vari??t?? de fonctions (lin??aire, exponentielle, etc.). Une fa??on pratique de le faire, sans ralentir les calculs, est d'utiliser le nombre d'it??rations ex??cut??es comme une entr??e ?? une table palette de couleurs consultation initialis?? au d??marrage. Si la table de couleur a, par exemple, 500 entr??es, alors vous pouvez utiliser n mod 500, o?? n est le nombre d'it??rations, pour s??lectionner la couleur ?? utiliser. Vous pouvez initialiser la matrice de palette de couleurs de diff??rentes mani??res, en fonction de ce particularit?? du comportement de fuite que vous voulez souligner graphiquement.
Continu (lisse) colorant
The Escape Temps algorithme est populaire pour sa simplicit??. Toutefois, il cr??e des bandes de couleur, ce qui peut nuire ?? la valeur d'une image. Cela peut ??tre r??solu en utilisant l'algorithme normalis?? nombre d'it??rations, qui fournit une transition en douceur de couleurs entre les it??rations. L'??quation est
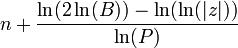
o?? n est le nombre d'it??rations pour z, B est le rayon de sauvetage (ce est normalement 2 pour un ensemble de Mandelbrot, mais il peut ??tre modifi??), et P est la puissance pour laquelle z est soulev??e ?? l'ensemble ??quation de Mandelbrot (z n = 1 z n + P c, P est g??n??ralement deux). Une autre ??quation pour cela est
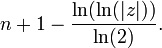
Notez que cette nouvelle ??quation est plus simple que le premier, mais il ne fonctionne que pour Mandelbrot avec un rayon de sauvetage de 2 et une puissance de 2.
Bien que cet algorithme est relativement simple ?? mettre en ??uvre (en utilisant soit l'??quation), il ya quelques choses qui doivent ??tre pris en consid??ration. Tout d'abord, les deux ??quations renvoient un flux continu de nombres. Cependant, il est ?? vous de d??cider comment les valeurs de retour seront convertis en une couleur. Certains type de m??thode pour la coul??e de ces chiffres sur un gradient devrait ??tre ??labor??. Deuxi??mement, il est recommand?? que quelques it??rations suppl??mentaires sont effectu??es de telle sorte que z peut se d??velopper. Si vous arr??tez it??ration d??s que z ??vasions, il ya la possibilit?? que l'algorithme de lissage ne fonctionnera pas.
Les estimations de distance
On peut calculer la distance du point c (en ou ext??rieur int??rieur) au point de la plus proche limite d'ensemble de Mandelbrot.
Ext??rieur estimation ?? distance
La preuve de la connectivit?? de l'ensemble de Mandelbrot donne en fait une formule pour la uniformisation de la carte compl??ment  (Et le d??riv?? de cette carte). Par le Koebe 1/4 th??or??me, on peut alors estimer la distance entre le point m??dian de notre pixel et l'ensemble de Mandelbrot jusqu'?? un facteur de quatre.
(Et le d??riv?? de cette carte). Par le Koebe 1/4 th??or??me, on peut alors estimer la distance entre le point m??dian de notre pixel et l'ensemble de Mandelbrot jusqu'?? un facteur de quatre.
En d'autres termes, ?? condition que le nombre maximal d'it??rations est suffisamment ??lev??e, on obtient une image de l'ensemble de Mandelbrot avec les propri??t??s suivantes:
- Chaque pixel qui contient un point de l'ensemble de Mandelbrot est de couleur noire.
- Chaque pixel qui est de couleur noire est proche de l'ensemble de Mandelbrot.
L'estimation de la distance d'un pixel c (un nombre complexe) de l'ensemble de Mandelbrot est donn??e par
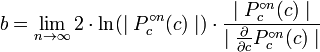
o??
 signifie polyn??me quadratique complexe
signifie polyn??me quadratique complexe 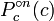 signifie n it??rations de
signifie n it??rations de 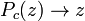 ou
ou  , ?? commencer par z = c:
, ?? commencer par z = c: 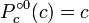 ,
, 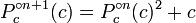 ;
; 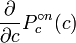 est la d??riv??e de
est la d??riv??e de 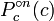 par rapport ?? c. Ce d??riv?? peut ??tre trouv??e en commen??ant par
par rapport ?? c. Ce d??riv?? peut ??tre trouv??e en commen??ant par 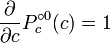 et puis
et puis  . Cela peut facilement ??tre v??rifi?? en utilisant la r??gle de la cha??ne pour le d??riv??.
. Cela peut facilement ??tre v??rifi?? en utilisant la r??gle de la cha??ne pour le d??riv??.
Du point de vue d'un math??maticien, cette formule ne fonctionne que dans la limite o?? n tend vers l'infini, mais les estimations tr??s raisonnables peut ??tre trouv?? avec quelques it??rations suppl??mentaires apr??s les principales sorties de boucle.
Une fois b se trouve, par le Koebe quart-th??or??me, nous savons qu'il ne ya pas de point de l'ensemble de Mandelbrot avec la distance de c plus petit que b / 4.
Int??rieur estimation de la distance
Il est ??galement possible d'estimer la distance d'un (ce est ?? dire, int??rieure) Point limitly p??riodique de la fronti??re de l'ensemble de Mandelbrot. L'estimation est donn??e par 
o??
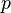 est la p??riode,
est la p??riode,  est le point qui doit ??tre estim??e,
est le point qui doit ??tre estim??e, 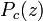 est le polyn??me quadratique complexe
est le polyn??me quadratique complexe 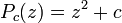
 est
est 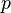 compositions de
compositions de 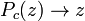 En commen??ant par
En commen??ant par 
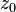 est l'une des caract??ristiques
est l'une des caract??ristiques 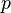 Le secteur qui rendent le attracteur des it??rations de
Le secteur qui rendent le attracteur des it??rations de 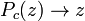 commen??ant par
commen??ant par 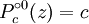 ;
; 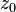 satisfait
satisfait 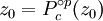 ,
,  ,
,  ,
,  et
et 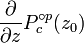 sont divers d??riv??s de
sont divers d??riv??s de 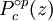 , ??valu?? ??
, ??valu?? ?? 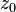 .
.
Donn?? 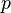 et
et 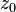 ,
,  et ses d??riv??s peuvent ??tre ??valu??s par:
et ses d??riv??s peuvent ??tre ??valu??s par:

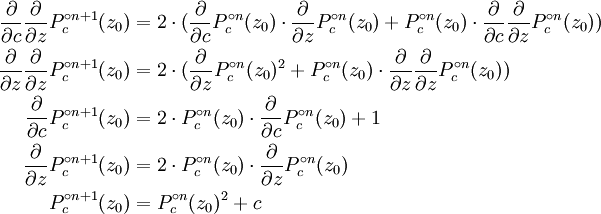 .
.
Analogue au bo??tier ext??rieur, une fois b est trouv??e, nous savons que tous les points de la distance de b / 4 c sont ?? l'int??rieur de l'ensemble de Mandelbrot.
Il ya deux probl??mes pratiques avec l'estimation de la distance int??rieure: d'abord, nous devons trouver 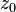 pr??cis??ment, et deuxi??mement, nous devons trouver
pr??cis??ment, et deuxi??mement, nous devons trouver 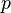 pr??cis??ment. Le probl??me avec
pr??cis??ment. Le probl??me avec 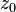 est que la convergence de
est que la convergence de 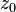 en it??rant
en it??rant 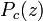 exige, en th??orie, un nombre infini d'op??rations. Le probl??me avec la p??riode est que, parfois, en raison d'erreurs d'arrondi, une p??riode est faussement identifi?? comme ??tant un multiple entier de la p??riode r??elle (par exemple, une p??riode de 86 est d??tect??e, tandis que la p??riode r??elle est seulement 43 = 86/2) . Dans ce cas, la distance est surestim??e, ce est ?? dire, le rayon rapport?? pourrait contenir des points en dehors de l'ensemble de Mandelbrot.
exige, en th??orie, un nombre infini d'op??rations. Le probl??me avec la p??riode est que, parfois, en raison d'erreurs d'arrondi, une p??riode est faussement identifi?? comme ??tant un multiple entier de la p??riode r??elle (par exemple, une p??riode de 86 est d??tect??e, tandis que la p??riode r??elle est seulement 43 = 86/2) . Dans ce cas, la distance est surestim??e, ce est ?? dire, le rayon rapport?? pourrait contenir des points en dehors de l'ensemble de Mandelbrot.
Optimisations
Une fa??on d'am??liorer les calculs est de savoir ?? l'avance si le point donn?? se trouve dans la cardio??de ou dans la p??riode de deux ampoule.
Pour ??viter d'avoir ?? faire un tr??s grand nombre d'it??rations pour les autres points de l'ensemble, on peut faire "v??rifier" la p??riodicit?? des moyens -Quels v??rifier si un point atteint en r??it??rant un pixel a ??t?? atteint avant. Si oui, le pixel ne peut pas se ??carter, et doit ??tre dans l'ensemble. Ce est la plus pertinente pour les calculs en virgule fixe, o?? il ya une chance relativement ??lev??e de cette p??riodicit??-plein virgule flottante (ou sup??rieur pr??cision) la mise en ??uvre serait rarement aller dans une telle p??riode.
P??riodicit?? v??rification est, bien s??r, un compromis: La n??cessit?? de rappeler les points co??te m??moire et de gestion de donn??es des instructions, alors qu'il enregistre des instructions de calcul



![z \ mapsto \ lambda z (z-1), \ quad \ lambda \ in [1,4]. \,](../../images/214/21446.png)