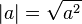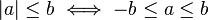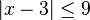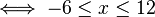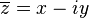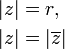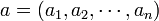Valeur absolue

Contexte des ??coles Wikip??dia

Cette s??lection se fait pour les ??coles par la charit?? pour enfants lire la suite . Avant de vous d??cider ?? propos de parrainer un enfant, pourquoi ne pas en apprendre davantage sur diff??rents organismes de parrainage premier ?

En math??matiques , la valeur absolue (ou module qui est latine pour une petite mesure) d'un nombre r??el est sa valeur num??rique sans ??gard ?? son signe . Ainsi, par exemple, la figure 3 est la valeur absolue de 3 fois et -3. Dans la programmation informatique , la fonction math??matique utilis??e pour effectuer ce calcul est habituellement donn?? le nom abs ().

G??n??ralisations de la valeur absolue de nombres r??els se produisent dans une grande vari??t?? de param??tres math??matiques. Par exemple une valeur absolue est ??galement d??finie pour les nombres complexes , la quaternions, cycles command??s, les champs et les espaces vectoriels . La valeur absolue est ??troitement li?? aux notions de amplitude, la distance , et norme dans diff??rents contextes physiques et math??matiques.

Le graphe de la fonction de valeur absolue pour les nombres r??els.

Nombres r??els

Pour tout nombre r??el la valeur absolue d'un module ou d'un est d??sign?? par | a |, et est d??finie comme

$| a | = \ begin {} un cas, et \ mbox {} si un \ ge 0 \\ -a, & \ mbox {} si un <0. \ end {} cas$

Comme on peut le voir d'apr??s la d??finition ci-dessus, la valeur absolue de a est toujours soit positive ou nulle , mais jamais n??gative .

D'un point de vue g??om??trique, la valeur absolue d'un nombre r??el est la distance le long de la v??ritable ligne de num??ro de ce nombre de z??ro, et, plus g??n??ralement, la valeur absolue de la diff??rence de deux nombres r??els est la distance entre eux. En effet, la notion d'un r??sum?? fonction de distance en math??matiques peut ??tre consid??r??e comme une g??n??ralisation de la valeur absolue de la diff??rence (voir ??Distance?? ci-dessous).

La proposition suivante, donne une identit?? qui est parfois utilis?? comme une alternative (et ??quivalent) d??finition de la valeur absolue:

Proposition 1:

$| A | = \ sqrt {a ^ 2}$

La valeur absolue a les quatre propri??t??s fondamentales suivantes:

Proposition 2:

$\| A \| \ ge 0$	Non-n??gativit??
$\| A \| = 0 \ ssi a = 0$	Positive-nettet??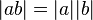
$\| Ab \| = \| a \|\| b \| \,$	Multiplicativeness
$\| A + b \| \ le \| a \| + \| B \|$	Sous-additivit??

D'autres propri??t??s importantes de la valeur absolue comprennent:

Proposition 3:

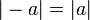
$\| -a \| = \| A \| \,$	Sym??trie
$\| A - b \| = 0 \ ssi a = b$	Identit?? des indiscernables (??quivalent ?? positive nettet??)
$\| A - b \| \ le \| a - c \| + \| c - b \|$	l'in??galit?? de Triangle (??quivalent ?? la sous-additivit??)
$\| A / b \| = \| a \| / \| b \| \ mbox {(si b} \ ne 0) \,$	Pr??servation de la division (??quivalent ?? multiplicativeness)
$\| A-b \| \ ge \|\| a \| - \| b \|\|$	(??quivalent ?? la sous-additivit??)

Deux autres in??galit??s sont utiles:

$| A | \ le b \ ssi -b \ le un \ le b$

$| A | \ ge b \ ssi a \ le -b \ mbox {} ou b \ le un$

Le ci-dessus sont souvent utilis??s dans la r??solution des in??galit??s; par exemple:

$\| X-3 \| \ le 9$	$\ Ssi -9 \ le x-3 \ le 9$
	$\ Ssi -6 \ le x \ le 12$

Les nombres complexes

La valeur absolue d'un nombre complexe z est la distance r de z ?? l'origine. Il est ??galement consid??r?? que l'image en z et z ont la m??me valeur absolue.

??tant donn?? que les nombres complexes ne sont pas ordonn??, la d??finition donn??e ci-dessus pour la valeur absolue r??elle ne peut pas ??tre directement g??n??ralis??e pour un nombre complexe. Cependant l'identit?? donn??e dans la Proposition 1:

$| A | = \ sqrt {a ^ 2}$

peut ??tre consid??r?? comme la motivation la d??finition suivante.

Pour tout nombre complexe

$z = x + iy, \,$

o?? x et y sont des nombres r??els, la valeur absolue ou module de z est not??e | z |, et est d??finie comme

$| Z | = \ sqrt {x ^ 2 + y ^ 2}.$

Il se ensuit que la valeur absolue d'un nombre r??el x est ??gal ?? sa valeur absolue consid??r?? comme un nombre complexe puisque:

$| X + i0 | = \ sqrt {x ^ 2 + 0 ^ 2} = \ sqrt {x ^ 2} = | x |.$

Comme pour l'interpr??tation g??om??trique de la valeur absolue pour les nombres r??els, il r??sulte de ce qui th??or??me de Pythagore que la valeur absolue d'un nombre complexe est la distance dans le plan complexe de ce nombre complexe de la origine, et plus g??n??ralement, que la valeur absolue de la diff??rence de deux nombres complexes est ??gale ?? la distance entre ces deux nombres complexes.

Les actions de valeur absolue complexes toutes les propri??t??s de la valeur absolue r??elle donn??s dans les propositions 2 et 3 ci-dessus. En outre, si

$z = x + i y = r (\ cos \ phi + i \ sin \ phi) \,$

$\ overline {z} = x - iy$

est le conjugu??e complexe de z, il est alors facile de voir que

$\ Begin {align} | z | = r &, \\ | z | = & | \ overline {z} | \ end {align}$

$| Z | = \ sqrt {z \ overline {z}},$

avec la derni??re formule ??tant l'analogue complexe de la proposition 1 mentionn?? ci-dessus dans le cas r??el.

Depuis les r??els positifs forment un sous-groupe des nombres complexes sous la multiplication, nous pouvons penser de la valeur absolue comme un endomorphisme de la groupe multiplicatif des nombres complexes.

Fonctions valeur absolue

La fonction r??elle de valeur absolue est continue partout. Il est diff??rentiable partout sauf pour x = 0. Il est monotone d??croissante sur l'intervalle (-∞, 0] et monotone croissante sur l'intervalle [0, ∞). Depuis un nombre r??el et son n??gatif ont la m??me valeur absolue, ce est un m??me fonctionner, et ne est donc pas inversible.

Le complexe fonction de valeur absolue est continue partout, mais (complexe) d??rivable nulle part (Une fa??on de voir ce est de montrer qu'il ne ob??it pas ?? la Cauchy-Riemann ??quations).

Les deux fonctions sont r??els et complexes idempotent.

C'est un fonction non lin??aire.

Anneaux command??s

La d??finition de la valeur absolue donn??e pour les nombres r??els ci-dessus peut facilement ??tre ??tendu ?? tout anneau command??. Autrement dit, si a est un ??l??ment d'un anneau R ordonn??, la valeur absolue d'une, not??e | a |, est d??finie comme ??tant:

$| A | = \ begin {} un cas, et \ mbox {} si un \ ge 0 \\ -a, & \ mbox {if} a <0, \ end {} cas$

o?? - a est la inverse additif d'un, et l'additif est 0 ??l??ment d'identit??.

Distance

La valeur absolue est ??troitement li??e ?? la notion de distance. Comme indiqu?? plus haut, la valeur absolue d'un nombre r??el ou complexe est la la distance ?? partir de ce nombre ?? l'origine, sur la ligne de nombre r??el, pour les nombres r??els, ou dans le plan complexe, pour des nombres complexes, et plus g??n??ralement, la valeur absolue de la diff??rence de deux nombres r??els ou complexes est la distance entre eux.

Le standard La distance euclidienne entre les deux points

$a = (a_1, a_2, \ cdots, a_n)$

$b = (b_1, b_2, \ cdots, b_n)$

dans euclidienne -space n est d??fini comme:

$\ Sqrt {(a_1-b_1) ^ 2 + (a_2-b_2) ^ 2 + \ cdots + (a_n-b_n) ^ 2}.$

Cela peut ??tre consid??r?? comme une g??n??ralisation de | a - b |, car si a et b sont r??els, puis par la proposition 1,

$| A - b | = \ sqrt {(a - b) ^ 2}$

tandis que si

$a = a_1 + i A_2 \,$

$b = b_1 + i b_2 \,$

sont des nombres complexes, puis

$\| A - b \| \,$	$= \| (A_1 + i A_2) - (+ i b_1 B_2) \| \,$
	$= \| (A_1 - b_1) + i (a_2 - b_2) \| \,$
	$= \ Sqrt {(a_1 - b_1) ^ 2 + (a_2 - b_2) ^ 2}$

Ce qui pr??c??de montre que la distance "valeur absolue" pour les nombres r??els ou des nombres complexes, d'accord avec la distance euclidienne norme h??ritent du fait de les consid??rer comme l'une et espaces euclidiens bidimensionnelles respectivement.

Les propri??t??s de la valeur absolue de la diff??rence de deux nombres r??els ou complexes: non-n??gativit??, l'identit?? des indiscernables, la sym??trie et l'in??galit?? de triangle donn?? dans les propositions 2 et 3 ci-dessus, peuvent ??tre vus ?? motiver la notion plus g??n??rale d'un fonction de distance de la mani??re suivante:

Une fonction r??elle d sur un ensemble X ?? X est appel??e une fonction de distance (ou une m??trique) sur X, si elle remplit les quatre axiomes suivants:

$d (a, b) \ ge 0$	Non-n??gativit??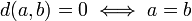
$d (a, b) = 0 \ ssi a = b$	Identit?? des indiscernables
$d (a, b) = D (B, A) \,$	Sym??trie
$d (a, b) \ le d (a, c) + d (c, b)$	Triangle in??galit??s

D??riv??s

Le d??riv?? de la fonction r??elle absolue de valeur est le fonction signum, sgn (x), qui est d??finie comme

$\ Sgn (x) = \ frac {x} {| x |},$

pour x ≠ 0. La fonction valeur absolue ne est pas diff??rentiable en x = 0. Lorsque la fonction valeur absolue d'un nombre r??el renvoie une valeur sans respect ?? son signe, la fonction de signe renvoie le signe d'un nombre sans rapport ?? sa valeur. Par cons??quent, x = sgn (x) abs (x). La fonction signe est une forme de la Fonction de Heaviside utilis?? dans le traitement de signal, d??finie comme suit:

$u (x) = \ begin {cas} 0, et x <0 \\ \ frac {1} {2}, & x = 0 \\ 1, et x> 0, \ end {} cas$

o?? la valeur de la fonction de Heaviside ?? z??ro est classique. Donc, pour tous les points non nuls sur le ligne r??elle de nombre,

$u (x) = \ frac {\ sgn (x) 1} {2}. \,$

La fonction valeur absolue n'a pas de concavit?? ?? tout moment, la fonction signe est constante ?? tous les points. Par cons??quent, la d??riv??e seconde de | x | par rapport ?? x est nul partout sauf z??ro, o?? elle ne est pas d??finie.

La fonction valeur absolue est ??galement int??grable. Son primitive est

$\ Int | x | dx = \ frac {x | x |} {2} + C.$

Les champs

Les propri??t??s fondamentales de la valeur absolue de nombres r??els donn??s dans la proposition 2 ci-dessus, peuvent ??tre utilis??s pour g??n??raliser la notion de valeur absolue ?? un champ arbitraire, comme suit.

Une fonction v de valeur r??elle sur un champ F est appel?? valeur absolue (??galement un module, l'ampleur, la valeur, ou l'??valuation) se il satisfait aux quatre axiomes suivants:

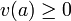
$v (a) \ ge 0$	Non-n??gativit??
$v (a) = 0 \ ssi a = \ mathbf {0}$	Positive-nettet??
$v (ab) = v (a) v (b) \,$	Multiplicativeness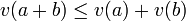
$v (a + b) \ le v (a) + v (b)$	Sous-additivit?? ou l'in??galit?? du triangle

O?? 0 repr??sente l'additif ??l??ment ayant une identit?? de F. Il r??sulte de caract??re d??fini positif et multiplicativeness que v (1) = 1, o?? 1 d??signe l'??l??ment neutre multiplicatif F. Les valeurs absolues r??elles et complexes d??finis ci-dessus sont des exemples de valeurs absolues pour un champ arbitraire.

Si v est une valeur absolue sur F, alors la fonction d de F ?? F, d??finie par d (a, b) v = (a - b), est une m??trique et les suivantes sont ??quivalentes:

d satisfait les in??galit?? ultram??trique d (x, y) <max {d (x, z), d (y, z)}.

$\ Big \ {c \ Big ({\ textstyle \ sum_ {k = 1} ^ n} \ mathbf {1} \ Big): n \ in \ mathbb {N} \ big \}$ est born??e dans R.

$v \ Big ({\ textstyle \ sum_ {k = 1} ^ n} \ mathbf {1} \ Big) \ le 1 \ text {} pour chaque n \ in \ mathbb {N}.$

$v (a) \ le 1 \ Rightarrow v (1 + a) \ le 1 \ text {} pour tous a \ in F.$

$v (a + b) \ le \ mathrm {max} \ {v (a), v (b) \} \ text {} pour tous a, b \ in F.$

Une valeur absolue qui satisfait tout (d'o?? la totalit??) des conditions ci-dessus est dite non-Archim??de, sinon il est dit Archim??de.

Espaces vectoriels

Encore une fois les propri??t??s fondamentales de la valeur absolue de nombres r??els peuvent ??tre utilis??s, avec une l??g??re modification, de g??n??raliser la notion d'un espace vectoriel arbitraire.

Une fonction r??elle || ?? || sur un espace vectoriel V sur un champ F, est appel?? une valeur absolue (ou plus g??n??ralement une norme) se il satisfait aux axiomes suivants:

Pour toutes dans un F, et v, u en V,

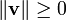
$\ \| \ Mathbf {v} \ \| \ ge 0$	Non-n??gativit??
$\ \| \ Mathbf {v} \ \| = 0 \ ssi \ mathbf {v} = 0$	Positive-nettet??
$\ \| A \ mathbf {v} \ \| = \| a \| \ \| \ mathbf {v} \ \|$	Homog??n??it?? positive ou ??volutivit?? positif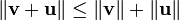
$\ \| \ Mathbf {v} + \ mathbf {u} \ \| \ le \ \| \ mathbf {v} \ \| + \ \| \ mathbf {u} \ \|$	Sous-additivit?? ou in??galit?? triangulaire

La norme d'un vecteur est aussi appel?? sa longueur ou l'ampleur.

Dans le cas de l'espace euclidien R ^n, la fonction d??finie par

$\ | (X_1, x_2, \ cdots, x_n) \ | = \ sqrt {\ sum_ {i = 1} ^ {n} (x_i) ^ 2}$

est une norme appel??e Norme euclidienne. Lorsque le nombre r??el R sont consid??r??s comme l'espace unidimensionnel vecteur R ¹ , la valeur absolue est un norme, et est le p -norme pour tout p. En fait, la valeur absolue est la norme "seulement" sur R ^1, dans le sens o??, pour chaque norme || ?? || sur R ^1, || x || = || 1 || ?? | x |. La valeur absolue complexe est un cas particulier de la norme dans un espace int??rieur du produit. Elle est identique ?? la norme euclidienne, si le plan complexe est identifi?? avec le plan euclidien R ^2.

Algorithmes

Dans le langage de programmation C , l' abs() , labs() , llabs() (en C99), fabs() , fabsf() , et fabsl() fonctions calculent la valeur absolue d'un op??rande. Codage la version enti??re de la fonction est trivial, ignorant le cas limite o?? le plus grand entier n??gatif est entr??e:

 int abs (int i)
 {
     si (i <0)
         retourner -i;
     autre
         retourner i;
 }

Le versions ?? virgule flottante sont plus d??licat, car ils doivent composer avec des codes sp??ciaux pour et infinis not-a-number.

La fonction de la valeur absolue Fortran, Matlab, et GNU Octave est abs . Il g??re entier, r??el ainsi que des nombres complexes.

Utilisation langage d'assemblage, il est possible de prendre la valeur absolue d'une inscrivez-vous en seulement trois instructions (par exemple indiqu??s pour un registre 32 bits sur un l'architecture x86, Intel syntaxe):

 cdq
 xor eax, edx
 eax sous, edx

cdq ??tend le bit de signe eax dans edx . Si eax est positive, alors edx devient nul, et les deux derni??res instructions ne ont pas effet, en laissant eax inchang??. Si eax est n??gative, alors edx devient 0xFFFFFFFF, ou -1. Les deux instructions suivantes deviennent alors une compl??ment ?? l'inversion de deux, ce qui donne la valeur absolue de la valeur n??gative dans eax .

R??cup??r?? ?? partir de " http://en.wikipedia.org/w/index.php?title=Absolute_value&oldid=209380665 "

$\| A - b \| \,$	$= \| (A_1 + i A_2) - (+ i b_1 B_2) \| \,$
	$= \| (A_1 - b_1) + i (a_2 - b_2) \| \,$
	$= \ Sqrt {(a_1 - b_1) ^ 2 + (a_2 - b_2) ^ 2}$