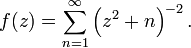Plan complexe
?? propos de ce ??coles s??lection Wikipedia
SOS Enfants a essay?? de rendre le contenu plus accessible Wikipedia par cette s??lection des ??coles. M??res SOS chaque regard apr??s une une famille d'enfants parrain??s .

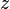 et son conjugu??
et son conjugu?? 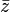 dans le plan complexe. La distance le long de la ligne bleu clair de l'origine au point z est le module ou la valeur absolue de z. L'angle φ est l'argument de z.
dans le plan complexe. La distance le long de la ligne bleu clair de l'origine au point z est le module ou la valeur absolue de z. L'angle φ est l'argument de z. En math??matiques , ou le plan z complexe Plane est une repr??sentation g??om??trique des nombres complexes ??tablies par l'axe r??el et imaginaire de l'axe orthogonal. Il peut ??tre consid??r?? comme une modification de plan cart??sien , avec la partie r??elle d'un nombre complexe repr??sent?? par un d??placement le long de l'axe x, et la partie imaginaire d'un d??placement le long de l'axe y.
Le plan complexe est parfois appel?? le plan Argand car il est utilis?? dans les diagrammes d'Argand. Ceux-ci sont nomm??s d'apr??s Jean-Robert Argand (1768-1822), m??me se ils ont d'abord ??t?? d??crits par l'arpenteur-norv??gienne danoise et math??maticien Caspar Wessel (1745-1818). Argand diagrammes sont fr??quemment utilis??s pour tracer les positions de la p??les et z??ros d'une fonction dans le plan complexe.
Le concept du plan complexe permet une interpr??tation g??om??trique des nombres complexes . Sous outre , ajoutent-ils comme des vecteurs . La multiplication de deux nombres complexes peut se exprimer plus facilement en coordonn??es polaires - l'ampleur ou module du produit est le produit des deux valeurs absolues , ou modules, et l'angle ou l'argument du produit est la somme des deux angles, ou des arguments. En particulier, la multiplication par un nombre complexe de module 1 agit comme une rotation.
Conventions de notation
En analyse complexe des nombres complexes sont habituellement repr??sent?? par le symbole imaginaires (y) parties, comme ce z, qui peut ??tre s??par?? de son v??ritable (x) et:
par exemple: z = 4 + 5 i,
o?? x et y sont des nombres r??els et i est l' unit?? imaginaire . Dans cette notation, ce nombre complexe z correspond au point (x, y) dans le plan cart??sien .
Dans le plan cart??sien, le point (x, y) peut ??galement ??tre repr??sent??e en coordonn??es polaires que
Dans le plan cart??sien, on peut supposer que le arctangente prend des valeurs de - π / 2 ?? π / 2 (en radians ) et un certain soin doit ??tre pris pour d??finir la fonction arctangente r??el pour les points (x, y) o?? x ≤ 0. Dans le plan complexe ces coordonn??es polaires prennent la forme
o??
Ici | z | est la valeur absolue ou module du nombre complexe z; θ, l'argument de z, est habituellement pris sur l'intervalle 0 ≤ θ <π 2; l'??galit?? et le dernier (?? | z | e iθ) est tir??e La formule d'Euler. Notez que l'argument de z est multi-valeurs, parce que la fonction exponentielle complexe est p??riodique, de p??riode 2 πi. Ainsi, si θ est une valeur de arg (z), les autres valeurs sont donn??es par arg (z) = θ + 2 nn, o?? n est un nombre entier ≠ 0.
La th??orie de la l'int??gration contour comprend une grande partie de l'analyse complexe. Dans ce contexte, la direction de Voyage autour d'une courbe ferm??e est important - inversion de la direction dans laquelle la courbe est travers??e multiplie la valeur de l'int??grale par -1. Par convention le sens positif est le sens antihoraire. Par exemple, le cercle unit?? est travers?? dans le sens positif quand nous commen??ons au point z = 1, puis voyage en haut et ?? gauche par le point z = i, puis vers le bas et vers la gauche ?? -1, puis vers le bas et vers la droite ?? travers - i, et enfin et vers la droite pour z = 1, o?? nous avons commenc??.
Presque tous analyse complexe est pr??occup?? par fonctions complexes - ce est, avec des fonctions qui mappent un sous-ensemble du plan complexe dans un autre sous-ensemble (??ventuellement chevauchement, ou m??me identiques) du plan complexe. Ici, il est d'usage de parler de la domaine de f (z) comme se trouvant dans la z-Plane, en se r??f??rant ?? la plage ou l'image de f (z) comme un ensemble de points dans l'Plane w. Dans symboles nous ??crivons
et r??fl??chir souvent de la fonction f comme une transformation de la z-Plane (avec des coordonn??es (x, y)) dans la Plane w (avec des coordonn??es (u, v)).
Projection st??r??ographique
Il peut ??tre utile de penser du plan complexe comme se il occupait la surface d'une sph??re. Etant donn?? une sph??re de rayon unit??, mettre le plan complexe droite passant par le milieu de celui-ci, de sorte que le centre de la sph??re co??ncide avec l'origine z = 0 sur le plan complexe, et l'??quateur de la sph??re co??ncide avec le cercle unit?? dans le plan .
Nous pouvons ??tablir une une-??-une correspondance entre les points sur la surface de la sph??re et les points du plan complexe de la mani??re suivante. Etant donn?? un point dans le plan, tracer une ligne droite reliant avec le p??le nord de la sph??re. Cette ligne traversera la surface de la sph??re dans exactement un autre point. Le point z = 0 sera projet?? sur le p??le sud de la sph??re. Depuis l'int??rieur du cercle unit?? se trouve ?? l'int??rieur de la sph??re, toute cette r??gion (| z | <1) sera mapp?? sur l'h??misph??re sud. L'unit?? cercle lui-m??me (| z | = 1) sera mapp?? sur l'??quateur, et l'ext??rieur du cercle unit?? (| z |> 1) sera mapp?? sur l'h??misph??re nord. Il est clair que cette proc??dure est r??versible - donn??e tout point de la surface de la sph??re qui ne est pas le p??le nord, nous pouvons tirer une ligne droite reliant ce point au p??le nord et coupant le plan plat dans exactement un point.
En vertu de cette projection st??r??ographique il ya juste un point le p??le nord lui-m??me - qui ne est pas associ??e ?? ne importe quel point dans le plan complexe. Nous perfectionnons la correspondance un-??-un en ajoutant un point de plus pour le plan complexe - le soi-disant point ?? l'infini -et l'associant avec le p??le nord de la sph??re. Cet espace topologique, le plan complexe, plus le point ?? l'infini, est connu comme le ??tendue plan complexe. Et ce est pourquoi les math??maticiens parlent d'un seul "point ?? l'infini" lors de l'examen analyse complexe. Il ya deux points ?? l'infini (positif et n??gatif) sur la ligne de nombre r??el, mais il ya un seul point ?? l'infini (le p??le nord) dans le plan complexe ??tendu.
Imaginez un instant ce qui va arriver aux lignes de latitude et de longitude lorsqu'ils sont projet??s de la sph??re sur le plan plat. Les lignes de latitude sont parall??les ?? l'??quateur, afin qu'ils deviennent des cercles parfaits centr??s sur l'origine z = 0. Et les lignes de longitude deviendra lignes droites passant par l'origine (et aussi par le "point ?? l'infini", depuis ils passent ?? la fois par les p??les nord et sud sur la sph??re).
Ce ne est pas la seule possible la situation st??r??ographique encore plausible de la projection d'une sph??re sur un plan constitu?? par deux ou plusieurs valeurs. Par exemple, le p??le nord de la sph??re peut ??tre plac?? sur le dessus de l'origine z = -1 dans un plan qui est tangent au cercle. Les d??tails ne importent pas vraiment. Toute projection st??r??ographique d'une sph??re sur un plan produira une "point ?? l'infini", et il permettra de cartographier les lignes de latitude et de longitude sur la sph??re dans les cercles et de lignes droites, respectivement, dans le plan.
Le plan de coupe
Lors de l'examen des fonctions d'une variable complexe, il est souvent commode de penser ?? une coupe dans le plan complexe. Cette id??e se pose naturellement dans plusieurs contextes diff??rents.
Les relations et les points de branchement ?? valeurs multiples
Consid??rons la relation simple ?? deux valeurs
Avant que nous puissions traiter cette relation comme une valeur unique fonction , la gamme de la valeur qui en r??sulte doit ??tre restreinte en quelque sorte. Lorsque vous traitez avec les racines carr??es de nombres r??els non n??gatifs cela se fait facilement. Par exemple, nous pouvons simplement d??finir
??tre le non-n??gative nombre r??el y tel que y 2 = x. Cette id??e ne fonctionne pas si bien dans le plan complexe ?? deux dimensions. Pour comprendre pourquoi, nous devons penser ?? la fa??on dont la valeur de f (z) varie comme le point z se d??place autour du cercle unit??. Nous pouvons ??crire
??videmment, comme z d??place tout le chemin autour du cercle, avec seulement des traces sur une moiti?? du cercle. Donc un mouvement continu dans le plan complexe a transform?? la racine carr??e positive e 0 = 1 dans la n??gative racine carr??e iπ e = -1.
Ce probl??me se pose parce que le point z = 0 a une seule racine carr??e, alors que tout autre nombre complexe z ≠ 0 a exactement deux racines carr??es. Sur la ligne de nombre r??el nous pourrions contourner ce probl??me en ??rigeant une ??barri??re?? au seul point x = 0. Un obstacle plus important est n??cessaire dans le plan complexe, pour ??viter tout contour ferm?? ?? partir entourant compl??tement le point de ramification z = 0. Cela se fait couramment en introduisant une coupure de branche; dans ce cas le "cut" pourrait se ??tendre ?? partir du point z = 0 long de l'axe r??el positif au point ?? l'infini, de sorte que l'argument de la variable z dans le plan de coupe est limit??e ?? la gamme 0 ≤ arg (z) < 2 π.
Nous pouvons maintenant donner une description compl??te de ?? w = z. Pour ce faire nous avons besoin de deux copies de la z-Plane, chacun d'entre eux couper le long de l'axe r??el. Sur une copie nous d??finissons la racine carr??e de 1 pour e 0 = 1, et de l'autre nous d??finissons la racine carr??e de 1 ?? ??tre iπ e = -1. Nous appelons ces deux copies des fiches compl??tes de plan de coupe. En faisant un argument de continuit??, nous voyons que la fonction (maintenant ?? valeur unique) w = z ?? mappe la premi??re feuille dans la moiti?? sup??rieure de la Plane de w, o?? 0 ≤ arg (w) <π, alors que la cartographie de la seconde feuille en la moiti?? inf??rieure de la w-Plane (o?? π ≤ arg (w) <π 2).
La coupure de branche dans cet exemple n'a pas ?? se trouver le long de l'axe r??el. Il n'a m??me pas besoin d'??tre une ligne droite. Toute courbe continue reliant l'origine z = 0 avec le point ?? l'infini pourrait fonctionner. Dans certains cas, la coupure de branche n'a m??me pas de passer par le point ?? l'infini. Par exemple, consid??rons la relation
Ici, le polyn??me z 2-1 dispara??t lorsque z = ?? 1, donc g a ??videmment deux points de branchement. Nous pouvons "couper" le plan le long de l'axe r??el, -1 ?? 1, et d'obtenir une feuille sur laquelle g (z) est une fonction ?? valeur unique. Alternativement, la coupe peut courir ?? partir de z = 1 le long de l'axe r??el positif ?? travers le point ?? l'infini, puis continuer "jusqu'??" l'axe r??el n??gatif ?? l'autre point de ramification, z = -1.
Cette situation est plus facilement visualis??s ?? l'aide de la projection st??r??ographique d??crit ci-dessus . Sur la sph??re une de ces coupes se ??tend longitudinalement ?? travers l'h??misph??re sud, reliant un point sur l'??quateur (z = -1) avec un autre point de l'??quateur (z = 1), et passant par le p??le sud (l'origine, z = 0) sur le chemin. La deuxi??me version de la coupe court longitudinalement ?? travers l'h??misph??re nord et relie les deux m??mes points ??quatoriales en passant par le p??le nord (ce est le point ?? l'infini).
Restreindre le domaine des fonctions m??romorphes
Un fonction m??romorphe est une fonction complexe qui est holomorphe et donc analytique partout dans son domaine, sauf ?? un ensemble fini, ou infini d??nombrable, nombre de points. Les points sur lesquels une telle fonction ne peut ??tre d??finie sont appel??s p??les de la fonction m??romorphe. Parfois, tous ces p??les se situent dans une ligne droite. Dans ce cas, les math??maticiens peuvent dire que la fonction est "holomorphe sur le plan de coupe". Voici un exemple simple.
Le fonction gamma, d??fini par
o?? γ est le Euler-Mascheroni constante et a des p??les simples ?? 0, -1, -2, -3, ... parce exactement un d??nominateur de la produit infini dispara??t lorsque z est z??ro ou un entier n??gatif. Depuis tous ses p??les sont situ??s sur l'axe r??el n??gatif, de z = 0 au point ?? l'infini, cette fonction pourrait ??tre d??crit comme
"Holomorphe sur le plan de coupe, la coupe se ??tendant le long de l'axe r??el n??gatif, de 0 (inclus) au point ?? l'infini."
En variante, Γ (z) peut ??tre d??crit comme
"Holomorphe dans le plan de coupe avec - π <arg (z) <π et en excluant le point z = 0."
Notez que cette coupe est l??g??rement diff??rente de la branche coup??e nous avons d??j?? rencontr??, car il exclut effectivement l'axe r??el n??gatif du plan de coupe. La coupure de branche gauche de l'axe r??el rapport avec le plan de coupe sur un c??t?? (0 ≤ θ), mais coup?? ?? partir du plan de coupe le long de l'autre c??t?? (θ <π 2).
Bien s??r, ce ne est pas vraiment n??cessaire d'exclure le segment entier de la ligne ?? partir de z = 0 ?? -∞ de construire un domaine dans lequel Γ (z) est holomorphe. Tout ce que nous devons vraiment faire, ce est la perforation de l'avion ?? un ensemble infini d??nombrable de points {0, -1, -2, -3, ...}. Mais un contour ferm?? dans le plan perfor?? peut entourer une ou plusieurs des p??les de Γ (z), ce qui donne un int??grale de contour qui ne est pas n??cessairement nul, par le th??or??me de r??sidus. En coupant le plan complexe nous nous assurons non seulement que Γ (z) est holomorphe dans ce domaine restreint - nous nous assurons ??galement que le contour int??grante de Γ sur toute courbe ferm??e situ??e dans le plan de coupe est identiquement ??gal ?? z??ro. Et cela peut ??tre important dans certains des arguments math??matiques.
Sp??cification r??gions de convergence
De nombreuses fonctions complexes sont d??finis par s??rie infinie, ou en fractions continues. Une consid??ration fondamentale dans l'analyse de ces expressions infiniment longue est d'identifier la partie du plan complexe dans lequel elles convergent vers une valeur finie. Une coupe dans le plan peut faciliter ce processus, comme les exemples suivants montrent.
Consid??rons la fonction d??finie par la s??rie infinie
Depuis z = 2 (- z) 2 pour chaque nombre complexe z, il est clair que f (z) est une m??me fonction de z, de sorte que l'analyse peut ??tre limit?? ?? une moiti?? du plan complexe. Et depuis que la s??rie ne est pas d??finie lorsque
il est logique de couper le plan le long de la totalit?? de l'axe imaginaire et ??tablir la convergence de cette s??rie o?? la partie r??elle de z ne est pas nul avant d'entreprendre la t??che plus ardue d'examiner f (z) lorsque z est un nombre imaginaire pur.
Dans cet exemple, la coupe est une simple commodit??, parce que les points sur lesquels la somme infinie ne est pas d??finie sont isol??s, et le plan de coupe peut ??tre remplac?? par un plan convenablement perfor??. Dans certains contextes, la coupe est n??cessaire, et pas seulement pratique. Envisager l'infini fraction continue p??riodique
Il peut ??tre d??montr?? que f (z) converge vers une valeur finie si et seulement si z est pas un nombre r??el n??gatif tels que z <-??. En d'autres termes, la zone de convergence pour cette fraction continue est le plan de coupe, o?? la coupe se ??tend le long de l'axe r??el n??gatif, de -?? au point ?? l'infini.
Collage le plan de coupe de retour ensemble
Nous avons d??j?? vu comment la relation
peut ??tre transform?? en une fonction ?? valeur unique en divisant le domaine de f en deux feuilles d??connect??s. Il est ??galement possible pour "coller" ces deux feuilles de retour ensemble pour former une surface de Riemann unique sur lequel f (z) = z 1/2 peut ??tre d??fini comme une fonction holomorphe dont l'image est l'ensemble w-Plane (sauf pour le point w = 0). Voici comment cela fonctionne.
Imaginez deux copies du plan complexe couper, les coupes se ??tendant le long de l'axe r??el positif de z = 0 au point ?? l'infini. Sur une feuille de d??finir 0 ≤ arg (z) <π 2, de sorte que 1 1/2 = e 0 = 1, par d??finition. Sur la seconde feuille d??finir π ≤ 2 arg (z) <4 π, de sorte que 1 1/2 = e iπ = -1, encore une fois, par d??finition. Maintenant retourner la seconde feuille ?? l'envers, de sorte que les points d'axe imaginaire dans la direction oppos??e de l'axe imaginaire sur la premi??re feuille, avec les deux axes r??els pointant dans la m??me direction, et "colle" les deux feuilles ensemble (de sorte que le bord sur la premi??re feuille marqu??e "θ = 0" est reli??e au bord ??tiquet?? "θ <π 4" sur la deuxi??me feuille, et le bord de la seconde feuille marqu??e "θ = π 2" est reli??e au bord ??tiquet?? "θ <2 π "sur la premi??re feuille). Le r??sultat est le domaine de surface de Riemann sur lequel f (z) = z moiti?? est ?? valeur unique et holomorphe (sauf lorsque z = 0).
Pour comprendre pourquoi f est ?? valeur unique dans ce domaine, imaginer un circuit autour du cercle unit??, en commen??ant par z = 1 sur la premi??re feuille. Lorsque 0 ≤ θ <π 2 nous sommes toujours sur la premi??re feuille. Lorsque θ = 2 π nous avons travers?? sur la deuxi??me feuille, et nous sommes oblig??s de faire un deuxi??me circuit complet autour du point de ramification z = 0 avant de revenir ?? notre point de d??part, o?? θ = 4 π est ??quivalent ?? θ = 0, parce de la fa??on dont nous coll?? les deux feuilles ensemble. En d'autres termes, que la variable z fait deux tours complets autour du point de branche, l'image de z dans le w-Plane retrace juste un cercle complet.
La diff??renciation formelle montre que
?? partir de laquelle on peut conclure que la d??riv??e de f existe et est finie partout sur la surface de Riemann, sauf lorsque z = 0 (ce est-f est holomorphe, sauf lorsque z = 0).
Comment peut surface de Riemann de la fonction
??galement discut?? ci-dessus , ??tre construit? Une fois de plus nous commen??ons avec deux copies de la z-Plane, mais cette fois chacun est coup?? le long du segment de droite r??elle se ??tendant de z = -1 ?? z = 1 - ce sont les deux points de g (z) de la branche. Nous renversons un de ces t??te en bas, de sorte que les deux axes imaginaires signalons dans des directions oppos??es, et coller les bords correspondants des deux feuilles coup??es ensemble. Nous pouvons v??rifier que g est une fonction ?? valeur unique sur cette surface en tra??ant un circuit autour d'un cercle de rayon unit?? centr?? ?? z = 1. Commen??ant au point z = 2 sur la premi??re feuille mi-chemin nous nous tournons autour du cercle avant de rencontrer le couper en z = 0. Les forces de coupe-nous sur la deuxi??me feuille, de sorte que lorsque z a trac?? un tour complet autour du point de branche z = 1, w a pris juste une moiti?? d'un tour complet, le signe de w a ??t?? invers??e (depuis iπ e = -1), et notre chemin nous a pris au point z = 2 sur la deuxi??me feuille de la surface. Poursuivant ?? travers un demi-tour, nous rencontrons l'autre c??t?? de la coupe, o?? z = 0, et enfin atteindre notre point de d??part (z = 2 sur la premi??re feuille) apr??s avoir fait deux tours complets autour du point de branche.
La fa??on naturelle d'??tiqueter θ = arg (z) dans cet exemple est de mettre - π <θ ≤ π sur la premi??re feuille, avec π <π θ ≤ 3 sur la seconde. Les axes imaginaires sur les deux feuilles pointent dans des directions oppos??es de sorte que le sens de rotation anti-horaire positif est conserv??e comme un contour ferm?? se d??place d'une feuille ?? l'autre (se rappeler, la seconde feuille est ?? l'envers). Imaginons cette surface noy??e dans un espace ?? trois dimensions, avec les deux feuilles parall??les ?? la Plane xy. Ensuite, il semble y avoir un trou vertical dans la surface, o?? les deux d??coupes sont assembl??es. Que faire si la coupe est faite ?? partir de z = -1 long de l'axe r??el au point ?? l'infini, et ?? partir de z = 1, l'axe r??el jusqu'?? ce que la coupe se retrouve? . Encore une fois une surface de Riemann peut ??tre construite, mais cette fois le ??trou?? est horizontale topologiquement parlant , les deux versions de cette surface de Riemann sont ??quivalentes - ils sont surfaces bidimensionnelles de orientables une genre.
Utilisation du plan complexe dans la th??orie du contr??le
En th??orie du contr??le , une utilisation du plan complexe est connu comme le 's-plan. Il est utilis?? pour visualiser les racines de l'??quation d??crivant le comportement d'un syst??me (le ??quation caract??ristique) graphiquement. L'??quation est normalement exprim??e par un polyn??me dans le param??tre "s" de la Transform??e de Laplace, d'o?? le 's' nom avion.
Une autre utilisation correspondant du plan complexe est avec le Crit??re de stabilit?? de Nyquist. Ce est un principe g??om??trique qui permet la stabilit?? d'un syst??me de commande ?? d??terminer par une inspection Nyquist parcelle de sa r??ponse en fr??quence de phase (ou fonction de transfert) dans le plan complexe.
Le "plan z 'est une version en temps discret de la s-plan, o?? z transform??es sont utilis??es au lieu de la transformation de Laplace.
Autres significations de "plan complexe"
Les sections pr??c??dentes de cet article traitent avec le plan complexe que l'analogue g??om??trique des nombres complexes. Bien que cette utilisation du terme "plan complexe" a une histoire longue et riche math??matiquement, il ne est nullement le seul concept math??matique qui peut ??tre caract??ris?? comme ??le plan complexe". Il existe au moins trois possibilit??s suppl??mentaires.
- 1 + 1 dimensions L'espace de Minkowski, ??galement connu sous le plan de s??paration du complexe, est un "plan complexe" dans le sens o?? la alg??brique num??ros de d??doubl?? complexe peuvent ??tre s??par??s en deux composantes r??elles qui sont facilement associ??s au point (x, y) dans le plan cart??sien.
- L'ensemble des deux num??ros sur les r??els peuvent ??galement ??tre plac??s en correspondance un-??-un avec les points (x, y) du plan cart??sien, et repr??sentent un autre exemple d'un ??plan complexe".
- L'espace vectoriel C ?? C, le Produit cart??sien des nombres complexes avec eux-m??mes, est aussi un "plan complexe" dans le sens o?? il se agit d'un espace vectoriel ?? deux dimensions dont les coordonn??es sont des nombres complexes.

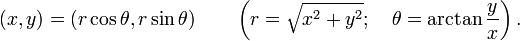
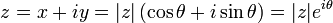
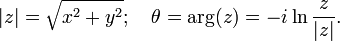

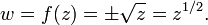
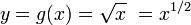
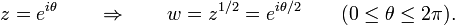
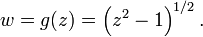
![\ Gamma (z) = \ frac {e ^ {- \ gamma z}} {z} \ prod_ {n = 1} ^ \ infty \ left [\ left (1+ \ frac {z} {n} \ right) ^ {- 1} e {^ z / n} \ right] \,](../../images/992/99216.png)