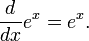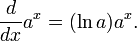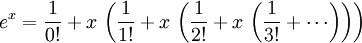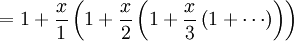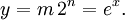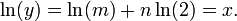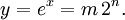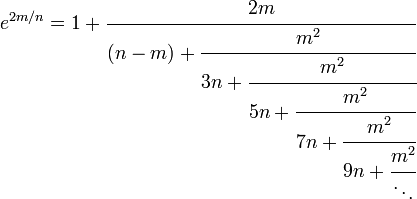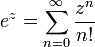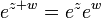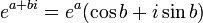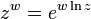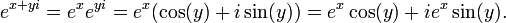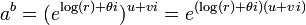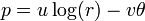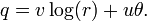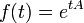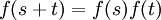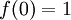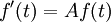Fonction exponentielle
Saviez-vous ...
Cette s??lection Wikipedia est d??connect?? disponibles ?? partir enfants SOS pour la distribution dans le monde en d??veloppement. Parrainage d'enfants aide les enfants du monde en d??veloppement ?? apprendre aussi.
La fonction exponentielle est une fonction dans les math??matiques . L'application de cette fonction pour une valeur x se ??crit exp (x). ??quivalente, ce qui peut ??tre ??crit sous la forme e x, o?? e est une constante math??matique, le base du logarithme naturel, qui est approximativement ??gale ?? 2,718281828, et est ??galement connu comme Euler num??ro.

En fonction des r??els x variable, le graphique de y = x e est toujours positive (au-dessus de l'axe des x) et en augmentant (vue de gauche ?? droite). Il ne touche jamais l'axe x, m??me si elle obtient arbitrairement proche (ainsi, l'axe des x est un axe horizontal asymptote de la courbe). Sa fonction inverse , le logarithme naturel , ln (x), est d??fini pour tout x positif. La fonction exponentielle est parfois d??nomm?? anti-logarithme . Toutefois, cette terminologie semble ??tre tomb?? en d??su??tude ces derniers temps.
Parfois, en particulier dans les sciences , la fonction terme exponentiel est plus g??n??ralement utilis?? pour des fonctions de la forme ka x, o?? a, appel?? la base, est un nombre r??el positif non ??gal ?? un. Cet article se concentrera initialement sur la fonction exponentielle avec la base e, nombre d'Euler.
En g??n??ral, la x variables peuvent ??tre ne importe quel r??el ou nombre complexe , ou m??me un tout autre genre d'objet math??matique; voir le d??finition formelle ci-dessous .
Propri??t??s
Plus simplement, les fonctions exponentielles se multiplient ?? une vitesse constante. Par exemple, la population d'une culture bact??rienne qui double tous les 20 minutes peut (approximativement, que ce ne est pas vraiment un probl??me continu) ??tre exprim??e comme une exponentielle, tout comme la valeur d'une voiture qui diminue de 10% par ann??e.
En utilisant le logarithme naturel, on peut d??finir des fonctions exponentielles plus g??n??rales. La fonction
d??fini pour tous a> 0 et tous les nombres r??els x, on appelle la fonction exponentielle avec la base a. A noter que cette d??finition de 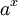 repose sur l'existence pr??alablement ??tablie de la fonction
repose sur l'existence pr??alablement ??tablie de la fonction 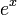 , D??finie pour tous les nombres r??els. (Ici, nous ne avons ni formellement, ni conceptuellement pr??ciser si une telle fonction existe ou ce que les exposants non-naturelles sont cens?? signifier.)
, D??finie pour tous les nombres r??els. (Ici, nous ne avons ni formellement, ni conceptuellement pr??ciser si une telle fonction existe ou ce que les exposants non-naturelles sont cens?? signifier.)
Notez que l'??quation ci-dessus est valable pour a = e, puisque
Fonctions exponentielles "traduisent entre l'addition et la multiplication" comme il est exprim?? dans les trois premiers et le cinqui??me des lois exponentielles suivantes:
Ce sont valables pour tous positifs nombres r??els a et b, et tous les nombres x et y r??el. Expressions impliquant des fractions et racines peuvent souvent ??tre simplifi??es en utilisant la notation exponentielle:
et, pour tout a> 0, nombre r??el b, et un entier n> 1:
D??riv??s et les ??quations diff??rentielles
L'importance des fonctions exponentielles en math??matiques et les sciences se explique principalement par la propri??t?? de leurs d??riv??s . En particulier,
Ce est, e x est son propre d??riv?? . Fonctions de la forme  pour la constante K sont les seules fonctions avec cette propri??t??. (Cela d??coule du Th??or??me de Cauchy-Lipschitz, avec
pour la constante K sont les seules fonctions avec cette propri??t??. (Cela d??coule du Th??or??me de Cauchy-Lipschitz, avec  et
et 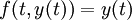 .) D'autres fa??ons de dire la m??me chose comprennent:
.) D'autres fa??ons de dire la m??me chose comprennent:
- La pente de la courbe en tout point est la hauteur de la fonction ?? ce moment.
- Le taux d'augmentation de la fonction au point x est ??gal ?? la valeur de la fonction en x.
- La fonction r??sout le ??quation diff??rentielle
 .
. - exp est un point fixe de d??riv??s, comme une fonctionnel
En fait, de nombreuses ??quations diff??rentielles donnent naissance ?? des fonctions exponentielles, y compris la ??quation et le Schr??dinger L'??quation de Laplace ainsi que les ??quations pour mouvement harmonique simple.
Pour les fonctions exponentielles avec d'autres bases:
Ainsi, toute fonction exponentielle est un multiple constant de son d??riv??.
Si le taux de croissance ou de d??croissance d'une variable est proportionnelle ?? sa taille - comme ce est le cas de la croissance illimit??e de la population (voir Catastrophe malthusienne), contin??ment compos?? int??r??t ou d??sint??gration radioactive - alors la variable peut ??tre ??crit comme une constante fois une fonction exponentielle du temps.
En outre, pour toute fonction diff??rentiable f (x), on trouve, par le r??gle de la cha??ne:
D??finition formelle

La fonction exponentielle e x peut ??tre d??finie de diff??rentes fa??ons ??quivalentes, en tant que s??rie infinie. En particulier, il peut ??tre d??fini par une s??rie de puissance :
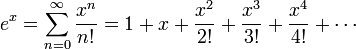 .
.
Notez que cette d??finition a la forme d'une s??rie de Taylor . Utiliser une autre d??finition de la fonction exponentielle devrait conduire au m??me r??sultat lorsqu'il est d??ploy?? comme une s??rie de Taylor .
Une d??finition moins commune d??finit  comme la solution
comme la solution 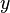 ?? l'??quation
?? l'??quation
Valeur num??rique
Pour obtenir la valeur num??rique de la fonction exponentielle, la s??rie infinie peut ??tre r????crite comme:
Cette expression converger rapidement si nous pouvons nous assurer que x est inf??rieur ?? un.
Pour ce faire, nous pouvons utiliser l'identit?? suivante.
- Click on the following link to visit or download this HTML page


![\, = E ^ z \ times \ left [{1 \ over 0!} + F \, \ left ({1 \ over 1!} + F \, \ left ({1 \ over 2!} + F \, \ gauche ({1 \ over 3!} + \ cdots \ right) \ right) \ right) \ right]](../../images/90/9079.png)
- O??
 est la partie enti??re de
est la partie enti??re de 
- O??
 est la partie fractionnaire de
est la partie fractionnaire de 
- De ce fait,
 est toujours inf??rieur ?? 1 et
est toujours inf??rieur ?? 1 et  et
et  ajouter ??
ajouter ??  .
.
La valeur de la constante e z peut ??tre calcul??e ?? l'avance en multipliant e z fois avec elle-m??me.
Informatique exp (x) pour x r??el
Une meilleure algorithme peut ??tre trouv?? comme suit.
Tout d'abord, notez que la r??ponse y = e x est g??n??ralement un nombre ?? virgule flottante repr??sent?? par un mantisse m et un exposant n donc y = m 2 n pour un entier n et convenablement petite m. Ainsi, nous obtenons:
Prenant journal sur les deux c??t??s des deux derni??re nous donne:
Ainsi, nous obtenons n que le r??sultat de la division de x par log (2) et de trouver le plus grand entier qui ne est pas sup??rieure ?? ce - ce est la fonction de chauss??e:
Ayant trouv?? n nous pouvons alors trouver la partie fractionnaire u comme ceci:
Le nombre u est petit et dans la gamme 0 ≤ u <ln (2) et ainsi nous pouvons utiliser la s??rie mentionn?? pr??c??demment pour calculer m:
Ayant constat?? m et n nous pouvons produire ensuite y simplement en combinant ces deux en un nombre ?? virgule flottante:
Fractions continues pour e x
Via l'identit?? d'Euler:
Des techniques plus avanc??es sont n??cessaires pour construire le suivant:
R??glage m = x et n = 2 rendements
Calcul du  pour nombre naturel (entier positif) n
pour nombre naturel (entier positif) n
Il est un moyen rapide pour calculer  lorsque n est un entier positif. Il se sert du fait que les essais qu'un tel nombre est impair est tr??s facile sur un ordinateur et en divisant par 2 est ??galement rapide en d??pla??ant simplement tous les bits vers la droite.
lorsque n est un entier positif. Il se sert du fait que les essais qu'un tel nombre est impair est tr??s facile sur un ordinateur et en divisant par 2 est ??galement rapide en d??pla??ant simplement tous les bits vers la droite.
??tape 1, initialiser certaines variables
y: = 1, k: = n, f: = a
??tape 2, le test k
si k est 0, passez ?? l'??tape 7
??tape 3, (k ne est pas ici 0, test si k est pair)
si k est m??me aller ?? l'??tape 5
??tape 4, (k est impair ici, se multiplient dans) 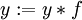
??tape 5, (fracture de 2 k / ignore reste, diviser par quart de travail, f ??galement carr??)
k: k = d??calage ?? droite par une f: f = f *
l'??tape 6, (boucle)
retournez ?? l'??tape 2
??tape 7, (fait, y est un r??sultat = n)
y retourner
En C , vous pouvez ??crire l'algorithme comme ceci:
alimentation double (double a, unsigned int n) {double-y = 1; à double f = a; unsigned int k = n; while (k = 0!) {if ((k & 1) = 0!) y * = f; >> k = 1; f = f *; } Return y; }alimentation double (double a, unsigned int n) {double-y = 1; à double f = a; unsigned int k = n; while (k = 0!) {if ((k & 1) = 0!) y * = f; >> k = 1; f = f *; } Return y; }
Alors que la multiplication d'un na??f ^ 100 100 exigerait it??rations d'une boucle, cette multiplication d'une boucle it??re seulement 7 fois (Le num??ro 100 est ??crit en utilisant sept bits).
Cet algorithme peut ??tre facilement ??tendu pour les entiers sign??s par r??aliser les ??tapes suivantes avant et apr??s:
l'??tape 1. Si k est n??gatif, nier la valeur de sorte que nous obtenons un positif k. n se souvient encore de la valeur d'origine.
??tape 2. Effectuer le calcul ci-dessus pour 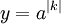
l'??tape 3. Si n est n??gatif, inverser le r??sultat si y: = 1 / y. y est maintenant le r??sultat de  pour un nombre entier n.
pour un nombre entier n.
Sur le plan complexe

Comme dans la vraie cas, la fonction exponentielle peut ??tre d??finie sur le plan complexe dans plusieurs formes ??quivalentes. Certaines de ces d??finitions miroir les formules pour la fonction exponentielle valeur r??elle. Plus pr??cis??ment, on peut encore utiliser la d??finition de la s??rie de puissance, o?? la valeur r??elle est remplac??e par un complexe:
Selon cette d??finition, il est facile de montrer pourquoi  tient dans le plan complexe.
tient dans le plan complexe.
Une autre d??finition ??tend la r??elle fonction exponentielle. Tout d'abord, nous d??clarons la propri??t?? d??sir??e 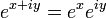 . Pour
. Pour  nous utilisons la r??elle fonction exponentielle. Nous proc??dons ensuite en d??finissant seulement:
nous utilisons la r??elle fonction exponentielle. Nous proc??dons ensuite en d??finissant seulement: 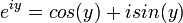 . Ainsi nous utilisons la r??elle d??finition plut??t que de l'ignorer.
. Ainsi nous utilisons la r??elle d??finition plut??t que de l'ignorer.
Consid??r??e comme une fonction d??finie sur le plan complexe , la fonction exponentielle conserve les propri??t??s importantes
pour tout z et w.
C'est un fonction holomorphe qui est p??riodique p??riode imaginaire  et peut ??tre ??crit comme
et peut ??tre ??crit comme
o?? a et b sont des valeurs r??elles. Cette formule relie la fonction exponentielle avec les fonctions trigonom??triques et de la fonctions hyperboliques. Ainsi, nous voyons que tous les fonctions ??l??mentaires, sauf pour les polyn??mes jaillir de la fonction exponentielle d'une mani??re ou d'une autre.
Voir ??galement La formule d'Euler.
??tendre le logarithme naturel ?? des arguments complexes donne une fonction multi-valeurs, ln (z). On peut alors d??finir une exponentiation plus g??n??ral:
pour tous les nombres complexes z et w. Ce est aussi une fonction multi-valeurs. Les lois exponentielles ci-dessus indiqu??es restent vrai si interpr??t?? correctement que les d??clarations sur les fonctions ?? valeurs multiples.
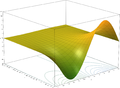
La fonction exponentielle cartes toute la ligne dans le plan complexe ?? un spirale logarithmique dans le plan complexe avec le centre ?? la origine. Deux cas particuliers peuvent ??tre not??es: lorsque la ligne d'origine est parall??le ?? l'axe r??el, l'sprial r??sultant ne se referme sur elle-m??me; quand la ligne d'origine est parall??le ?? l'axe imaginaire, la spirale qui en r??sulte est un cercle d'un rayon quelconque.
- Lots de la fonction exponentielle sur le plan complexe
Calcul de exp (z) pour un complexe z
Ce est assez simple compte tenu de la formule
Notez que l'argument y pour les fonctions trigonom??triques est r??el.
Calcul du 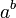 o?? a et b sont complexes
o?? a et b sont complexes
Ce est aussi simple ??tant donn?? les formules:
si a = x + yi et b = u + vi on peut convertir un premier ?? coordonn??es polaires en trouvant un  et un
et un  tel que:
tel que:
ou
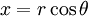 et
et 
Ainsi,  ou
ou  et
et  ou
ou 
Maintenant, nous avons ce qui suit:
donc:
L'exposant est donc une simple multiplication de deux valeurs complexes produisant un r??sultat complexe qui peut ensuite ??tre ramen?? au format cart??sien r??gulier par la formule:
o?? p est la partie r??elle de la multiplication:
et q est ??gal ?? la partie imaginaire de la multiplication:
Notez que toutes 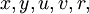
 ,
, 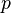 et
et 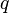 sont toutes les valeurs r??elles dans ces calculs. Le r??sultat de
sont toutes les valeurs r??elles dans ces calculs. Le r??sultat de 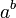 est donc
est donc  .
.
A noter ??galement que depuis que nous calculons et l'utilisation 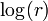 plut??t que de se r vous ne avez pas ?? calculer la racine carr??e. Au lieu de simplement calculer
plut??t que de se r vous ne avez pas ?? calculer la racine carr??e. Au lieu de simplement calculer  . M??fiez-vous des trop-plein potentiel si et ??ventuellement r??duire le x et y avant informatique
. M??fiez-vous des trop-plein potentiel si et ??ventuellement r??duire le x et y avant informatique  par une puissance de deux si appropri??
par une puissance de deux si appropri??  et
et 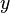 sont si grands que vous d??border. Si vous place courez le risque de d??bordement, l'??chelle par une puissance convenable de deux avant de calculer la somme des carr??s. Dans les deux cas, vous obtenez alors la version r??duite de
sont si grands que vous d??border. Si vous place courez le risque de d??bordement, l'??chelle par une puissance convenable de deux avant de calculer la somme des carr??s. Dans les deux cas, vous obtenez alors la version r??duite de  - Nous pouvons l'appeler
- Nous pouvons l'appeler 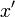 et la version r??duite de
et la version r??duite de 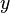 - Appelle
- Appelle 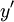 et ainsi vous obtenez:
et ainsi vous obtenez:
 et
et 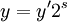
o?? 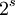 est le facteur d'??chelle.
est le facteur d'??chelle.
Ensuite, vous obtenez  o??
o?? 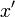 et
et 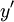 sont mis ?? l'??chelle de sorte que la somme des carr??s ne sera pas d??border ou n??gatif. Si
sont mis ?? l'??chelle de sorte que la somme des carr??s ne sera pas d??border ou n??gatif. Si  est tr??s grand alors
est tr??s grand alors 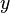 est tr??s faible de sorte que vous ne pouvez pas trouver un tel facteur d'??chelle vous d??border de toute fa??on et si la somme est sensiblement ??gale ??
est tr??s faible de sorte que vous ne pouvez pas trouver un tel facteur d'??chelle vous d??border de toute fa??on et si la somme est sensiblement ??gale ??  puisque y est ignor??e et donc vous obtenez
puisque y est ignor??e et donc vous obtenez 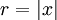 dans ce cas et
dans ce cas et  . La m??me chose arrive dans le cas o??
. La m??me chose arrive dans le cas o??  est tr??s faible et
est tr??s faible et 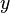 est tr??s grande. Si les deux sont tr??s grandes ou les deux sont tr??s petites, vous pouvez trouver un facteur d'??chelle tel que mentionn?? pr??c??demment.
est tr??s grande. Si les deux sont tr??s grandes ou les deux sont tr??s petites, vous pouvez trouver un facteur d'??chelle tel que mentionn?? pr??c??demment.
Notez que cette fonction est, en g??n??ral, plusieurs valeurs pour les arguments complexes. Ce est parce que la rotation d'un seul point ?? travers ne importe quel angle, plus 360 degr??s, ou 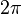 radians, est le m??me que l'angle de rotation ?? travers elle-m??me. Si
radians, est le m??me que l'angle de rotation ?? travers elle-m??me. Si  ci-dessus ne est pas unique:
ci-dessus ne est pas unique:  pour tout entier
pour tout entier 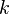 ferait ainsi. La convention est que, lorsque de
ferait ainsi. La convention est que, lorsque de 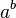 est pris comme une valeur unique, il doit ??tre que, pour
est pris comme une valeur unique, il doit ??tre que, pour 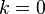 , Ie. nous utilisons la plus petite valeur possible (en amplitude) de th??ta, qui a une amplitude, au plus,
, Ie. nous utilisons la plus petite valeur possible (en amplitude) de th??ta, qui a une amplitude, au plus, 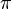 .
.
Matrices et alg??bres de Banach
La d??finition de la fonction exponentielle donn??e ci-dessus peut ??tre utilis?? pour chaque verbatim Alg??bre de Banach, et en particulier pour carr??s matrices (dans ce cas, la fonction est appel??e la matrice exponentielle). Dans ce cas, nous avons

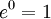
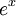 est inversible inverse
est inversible inverse 
- le d??riv?? de
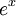 au point
au point  ce est que la carte lin??aire qui envoie
ce est que la carte lin??aire qui envoie  ??
?? 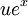 .
.
Dans le cadre des alg??bres de Banach non-commutatives, comme alg??bres de matrices ou des op??rateurs sur Banach ou Espaces de Hilbert, la fonction exponentielle est souvent consid??r??e comme une fonction d'un argument r??el:
o?? A est un ??l??ment fixe de l'alg??bre et t est un nombre r??el. Cette fonction a les propri??t??s importantes
Sur les alg??bres de Lie
Le exponentielle envoyant un Alg??bre de Lie ?? la groupe de Lie qui a donn?? lieu ?? elle partage les propri??t??s ci-dessus, ce qui explique la terminologie. En fait, depuis R est l'alg??bre de Lie du groupe de Lie de tous les nombres r??els positifs avec la multiplication, la fonction exponentielle ordinaire pour de vrais arguments est un cas particulier de la situation d'alg??bre de Lie. De m??me, depuis l'alg??bre de Lie M (n, R) de l'ensemble des matrices r??elles carr??s appartient au groupe de Lie de toutes les matrices carr??es inversibles, la fonction exponentielle pour les matrices carr??es est un cas particulier de la carte exponentielle alg??bre de Lie.
Double fonction exponentielle
La fonction exponentielle double terme peut avoir deux significations:
- une fonction avec deux termes exponentiels, avec diff??rents exposants
- une fonction
 ; cette pousse encore plus vite que d'une fonction exponentielle; Par exemple, si a = 10: f (-1) = 1,26, f (0) = 10, f (1) = 10 10, f (2) = 10 100 = googol, ..., f (100) = googolplex.
; cette pousse encore plus vite que d'une fonction exponentielle; Par exemple, si a = 10: f (-1) = 1,26, f (0) = 10, f (1) = 10 10, f (2) = 10 100 = googol, ..., f (100) = googolplex.
Factorielles croissent plus vite que les fonctions exponentielles, mais plus lentement que les fonctions doubles-exponentielle. Nombres de Fermat, g??n??r??s par 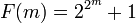 et num??ros doubles de Mersenne g??n??r??s par
et num??ros doubles de Mersenne g??n??r??s par  sont des exemples de fonctions exponentielles doubles.
sont des exemples de fonctions exponentielles doubles.
Propri??t??s similaires de  et la fonction
et la fonction 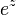
La fonction 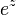 ne est pas dans C (z) (ie. pas le quotient de deux polyn??mes avec des coefficients complexes).
ne est pas dans C (z) (ie. pas le quotient de deux polyn??mes avec des coefficients complexes).
Pour les nombres complexes n distinctes  ,
, 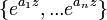 est lin??airement ind??pendants sur C (z).
est lin??airement ind??pendants sur C (z).
La fonction 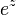 est transcendant sur C (z).
est transcendant sur C (z).
P??riodicit??
Pour tous les entiers n et x complexe:
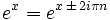
Preuve:

Pour tous les entiers positifs n et complexe a & x:
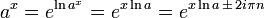

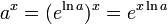


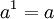
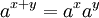
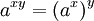


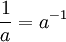
![\, \ Sqrt [n] {a ^ b} = \ left (\ sqrt [n] {a} \ right) ^ b = a ^ {b / n}.](../../images/90/9057.png)