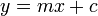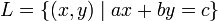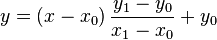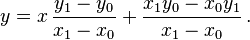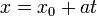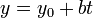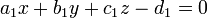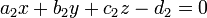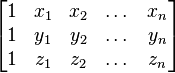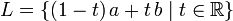Ligne (g??om??trie)

Contexte des ??coles Wikip??dia

Enfants SOS b??n??voles ont aid?? ?? choisir des articles et faites autre mat??riel de programme Cliquez ici pour plus d'informations sur les enfants SOS.

Trois lignes - les lignes rouges et bleues ont la m??me pente, tandis que les rouges et verts ont la m??me ordonn??e ?? l'origine.

Une repr??sentation d'une segment de ligne

G??om??trie
Oxyrhynchus papyrus (P.Oxy. I 29) montrant fragment de El??ments d'Euclide
Histoire de la g??om??trie
Branches La g??om??trie euclidienne ?? La g??om??trie non-euclidienne ?? g??om??trie analytique ?? G??om??trie riemannienne ?? G??om??trie diff??rentielle ?? La g??om??trie projective ?? G??om??trie alg??brique
Les domaines de recherche G??om??trie alg??brique ?? G??om??trie diff??rentielle ?? G??om??trie symplectique
Concepts importants Remarque ?? Ligne ?? Perpendiculaire ?? Parall??lement ?? Le segment de ligne ?? Ray ?? Avion ?? Longueur ?? Espace ?? Volume ?? Vertex ?? Angle ?? Congruence ?? Similarit?? ?? Polygone ?? Triangle ?? Altitude ?? ?? Hypot??nuse th??or??me de Pythagore ?? Quadrilat??re ?? Trap??ze ?? Kite ?? Parall??logramme ( Rhomboid, Rectangle, Rhombus, Place ) ?? Diagonal ?? Sym??trie ?? Curve ?? Cercle ?? Zone d'un disque ?? Circonf??rence ?? Diam??tre ?? Cylindre ?? Sph??re ?? Pyramide ?? Dimensions ( une, deux, trois, quatre)
G??om??tres Aryabhata ?? Ahm??s ?? Apolonius ?? Archim??de ?? Baudhayana ?? Bolyai ?? Brahmagupta ?? Euclid ?? Pythagore ?? Khayy??m ?? Descartes ?? Pascal ?? Euler ?? Gauss ?? Ibn al-Yasamin ?? Jyeṣṭhadeva ?? K??ty??yana ?? Lobachevsky ?? Manava ?? Minggatu ?? Riemann ?? Klein ?? Parameshvara ?? Poincar?? ?? Al-Sijzi ?? Hilbert ?? Minkowski ?? Cartan ?? Veblen ?? Sakabe Kōhan ?? Gromov ?? Atiyah ?? Virasena ?? Yang Hui ?? Yasuaki Aida ?? Zhang Heng

La notion de la ligne ou une ligne droite a ??t?? introduit par les math??maticiens anciens pour repr??senter objets droites avec la largeur et la profondeur n??gligeable. Les lignes sont une id??alisation de ces objets. Ainsi, jusqu'au XVIIe si??cle, les lignes ont ??t?? d??finies comme suit: "La ligne est la premi??re esp??ce de quantit??, qui a une seule dimension, ?? savoir la longueur, sans largeur ni la profondeur, et ne est rien d'autre que le d??bit ou la course du point qui [...] partira de son imaginaire d??placer quelque vestige de longueur, exon??r??e de toute la largeur. [...] La ligne droite est celle qui est aussi ??tendu entre ses points "

Euclid d??crit une ligne comme "longueur de sans largeur", et a introduit plusieurs postulats ind??montrables propri??t??s comme base ?? partir de laquelle il a construit la g??om??trie, qui se appelle maintenant la g??om??trie euclidienne pour ??viter toute confusion avec d'autres g??om??tries qui ont ??t?? introduites depuis la fin du XIXe si??cle (tels que non euclidienne g??om??trie, la g??om??trie projective, et la g??om??trie affine).

En math??matiques modernes, ??tant donn?? la multitude de g??om??tries, le concept d'une ligne est ??troitement li??e ?? la fa??on dont la g??om??trie est d??crite. Par exemple, dans la g??om??trie analytique , une ligne dans le plan est souvent d??finie comme l'ensemble des points dont les coordonn??es satisfaire une donn??e ??quation lin??aire , mais dans un cadre plus abstrait, comme g??om??trie incidence, une ligne peut ??tre un objet ind??pendant, distinct de l'ensemble des points qui se trouvent sur elle.

Quand une g??om??trie est d??crite par un ensemble de axiomes, la notion d'une ligne est g??n??ralement laiss?? ind??fini (un soi-disant objet primitif). Les propri??t??s des lignes sont alors d??termin??s par les axiomes qui se rapportent ?? eux. Un avantage de cette approche est la flexibilit?? qu'il offre aux utilisateurs de la g??om??trie. Ainsi, dans la g??om??trie diff??rentielle une ligne peut ??tre interpr??t?? comme un g??od??sique (chemin le plus court entre les points), tandis que dans certaines g??om??tries projectives une ligne est un espace vectoriel de dimension 2 (toutes les combinaisons lin??aires de deux vecteurs ind??pendants). Cette flexibilit?? se ??tend ??galement au-del?? des math??matiques et, par exemple, permet aux physiciens de penser ?? la trajectoire d'un rayon lumineux comme ??tant une ligne.

Un segment de ligne est une partie d'une ligne qui est d??limit?? par deux points d'extr??mit?? distinctes et contient tous les points sur la ligne entre ses points d'extr??mit??. Selon la fa??on dont le segment de ligne est d??finie, l'un des deux points d'extr??mit?? peuvent ou non faire partie du segment de ligne. Deux ou plusieurs segments de ligne peuvent avoir certains des m??mes relations que les lignes, comme ??tant parall??les, se croisant, ou l'inclinaison.

D??finitions contre descriptions

Toutes les d??finitions sont finalement circulaire dans la nature car ils d??pendent des concepts qui doivent eux-m??mes avoir des d??finitions, une d??pendance qui ne peut ??tre poursuivi ind??finiment sans revenir au point de d??part. Pour ??viter ce cercle vicieux certains concepts doivent ??tre prises concepts primitifs; termes qui sont pas donn?? de d??finition. En g??om??trie, il est souvent le cas que la notion de ligne est prise comme primitive. Dans les cas o?? une ligne est un concept d??fini, comme dans la g??om??trie des coordonn??es , quelques autres id??es fondamentales sont prises comme primitives. Lorsque le concept de ligne est une primitive, le comportement et les propri??t??s des lignes sont dict??es par la axiomes laquelle ils doivent satisfaire.

Dans un traitement axiomatique non axiomatique ou simplifi??e de la g??om??trie, la notion d'une notion primitive peut ??tre trop abstrait pour ??tre trait??es. Dans ce cas il est possible que la description ou l'image mentale d'une notion primitive est fourni pour donner une base pour construire la notion sur laquelle serait formellement ??tre fond??e sur les axiomes (implicites). Descriptions de ce type peuvent ??tre appel??s, par certains auteurs, que les d??finitions dans ce style informel de la pr??sentation. Ce ne sont pas de v??ritables d??finitions et ne pouvaient pas ??tre utilis??s dans les preuves formelles de d??clarations. La ??d??finition?? de la ligne dans les El??ments d'Euclide tombe dans cette cat??gorie. M??me dans le cas o?? une g??om??trie sp??cifique est envisag??e (par exemple, la g??om??trie euclidienne ), il ya un accord g??n??ralement accept??e parmi les auteurs ?? ce que une description informelle d'une ligne devrait ??tre lorsque le sujet ne est pas trait?? formellement.

La g??om??trie euclidienne

Lorsque la g??om??trie a ??t?? formalis??e par Euclide dans l' Elements , il a d??fini une ligne ?? ??tre ??longueur sans largeur" avec une ligne droite ??tant une ligne "qui se trouve uniform??ment avec les points sur elle-m??me??. Ces d??finitions ne sont gu??re utiles car ils utilisent des termes qui ne sont pas, eux-m??mes, d??finies. En fait, Euclide n'a pas utilis?? ces d??finitions dans ce travail et probablement les a inclus juste pour le rendre clair pour le lecteur ce qui a ??t?? discut??. Dans la g??om??trie moderne, une ligne est tout simplement consid??r?? comme un objet ayant des propri??t??s donn??es par axiomes, mais est parfois d??finie comme un ensemble de points ob??issant ?? une relation lin??aire lorsqu'une autre concept fondamental ne est pas d??finie.

Dans un formulation de la g??om??trie euclidienne ??vident, comme celui de Hilbert (axiomes d'Euclide originaux contenaient diverses failles qui ont ??t?? corrig??es par les math??maticiens modernes), une ligne est d??clar??e pr??senter certaines propri??t??s dont il se rapportent ?? d'autres lignes et Le secteur. Par exemple, pour deux points distincts, il ya une ligne unique, les contenant et des deux lignes distinctes se coupent en au plus un point. En deux dimensions, ?? savoir la euclidienne plan , deux lignes ne se croisent pas sont appel??s parall??le. En dimension sup??rieure, deux lignes qui ne se croisent pas peut ??tre parall??le si elles sont contenues dans un plan , ou biaiser se ils ne sont pas.

Toute collecte d'un nombre fini de lignes partitionne le plan en polygones convexes (??ventuellement illimit??e); cette cloison est connu comme un disposition de lignes.

Rayon

Compte tenu d'une ligne et un point A sur elle, nous pouvons consid??rer que la d??composition A cette ligne en deux parties. Chacune de ces parties est appel??e un rayon (ou demi-droite) et le point A est appel?? son point initial. Le point A est consid??r?? comme un membre du rayon. Intuitivement, un rayon est constitu?? de ces points sur une ligne passant par A et proc??dant ind??finiment, ?? partir de A, dans un seul sens le long de la ligne. Cependant, afin d'utiliser ce concept d'un rayon dans les preuves d'une d??finition plus pr??cise est n??cessaire.

Compte tenu des points distincts A et B, ils d??terminent un rayon unique avec initial point A. En deux points d??finissent une ligne unique, ce rayon est constitu??e de tous les points entre A et B (y compris a et b) et tous les points C sur la droite passant par A et B tel que B est entre A et C. Ceci est parfois ??galement exprim?? comme l'ensemble de tous les points C tel que A ne est pas entre B et C. Un point D, sur la ligne d??termin??e par A et B, mais pas dans le rayon avec l'initiale point A d??termin?? par B, d??terminera un autre rayon avec l'initiale point A. En ce qui concerne le rayon AB, AD rayon est appel??e le rayon oppos??.

Ainsi, nous dirions que deux points diff??rents, A et B, d??finissent une ligne et une d??composition de cette ligne dans le union disjointe d'un segment ouvert (A, B) et deux rayons, BC et AD (point D ne est pas ??tabli dans le diagramme, mais se trouve ?? gauche de A sur la ligne AB). Ce ne sont pas les rayons oppos??s car ils ont diff??rents points initiaux.

La d??finition d'un rayon d??pend de la notion de interm??diarit?? de points sur une ligne. Il se ensuit que les rayons ne existent que pour les g??om??tries pour lesquelles cette notion existe, g??n??ralement la g??om??trie euclidienne ou la g??om??trie affine sur une corps ordonn??. D'autre part, les rayons ne existent pas dans la g??om??trie projective ni dans une g??om??trie non sur une corps ordonn??, comme les nombres complexes ou tout champ fini.

En topologie , un rayon dans un espace X est un plongement continue R ⁺ → X. Il est utilis?? pour d??finir la notion importante de fin de l'espace.

Coordonner la g??om??trie

Dans la g??om??trie des coordonn??es , les lignes d'un plan cart??sien peuvent ??tre d??crites alg??briquement par des ??quations lin??aires . En deux dimensions, l'??quation pour les lignes non-verticales est souvent donn??e dans la forme d'une pente :

$y = mx + c \,$

o??:

m est le pente ou gradient de la ligne.

c est la ordonn??e ?? l'origine de la ligne.

x est le variable ind??pendante de la fonction y = f (x).

La pente de la ligne par les points A (x _a, y _a) et B (x _b, y _b), lorsque X _a ≠ x _b, est donn??e par m = _(b y -y _a) / _(b x -x _a) et de l'??quation de cette droite peut se ??crire y = m (x - x _a) + y _a.

Dans R ^2, chaque ligne L (y compris les lignes verticales) est d??crite par une ??quation lin??aire de la forme

$L = \ {(x, y) \ mi ax + by = c \} \,$

avec de vrais fixe les coefficients a, b et c de telle sorte que a et b ne sont pas tous deux z??ro. En utilisant ce formulaire, les lignes verticales correspondent aux ??quations avec b = 0.

Il existe de nombreuses variantes de mani??res d'??crire l'??quation d'une droite qui peuvent tous ??tre converti ?? partir d'un ?? l'autre par une manipulation alg??brique. Ces formes (voir l'??quation lin??aire pour les autres formes) sont g??n??ralement nomm??s par le type d'informations (donn??es) ?? propos de la ligne qui est n??cessaire pour ??crire la forme. Certaines des donn??es importantes d'une ligne est sa pente, x ?? l'origine, points connus sur la ligne et ordonn??e ?? l'origine.

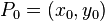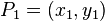L'??quation de la droite passant par deux points diff??rents $P_0 = (x_0, Y_0)$ et $P_1 = (x 1, y_1)$ peut se ??crire

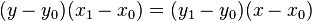$(Y - Y_0) (x_1 - x_0) = (y_1 - Y_0) (x - x_0)$ .

Si x ₀ ≠ x _1, cette ??quation peut ??tre r????crite comme

$y = (x-x_0) \, \ frac {y_1-Y_0} {} x_1-x_0 + Y_0$

$y = x \, \ frac {y_1-Y_0} {x_1-x_0} + \ frac {x_1y_0-x_0y_1} {x_1-x_0} \ ,.$

En trois dimensions, les lignes ne peuvent pas ??tre d??crites par une seule ??quation lin??aire, de sorte qu'ils sont souvent d??crits par ??quations param??triques:

$x = x 0 + ?? \,$

$y = Y_0 + bt \,$

$z = z_0 + ct \,$

o??:

x, y et z sont tous des fonctions de la variable ind??pendante t qui se ??tend sur les nombres r??els.

(X _0, y _0, z ₀₎ est un point quelconque de la ligne.

a, b, et c sont reli??es ?? la pente de la droite, de telle sorte que le vecteur (a, b, c) est parall??le ?? la ligne.

Ils peuvent ??galement ??tre d??crits comme des solutions simultan??e de deux ??quations lin??aires

$a_1x + b_1y + c_1z-d_1 = 0 \,$

$a_2x + b_2y + c_2z-d_2 = 0 \,$

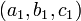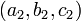tel que $(A_1, b_1, c_1)$ et $(A_2, b_2, c_2)$ ne sont pas proportionnelles (les relations $a_1 = ta_2, b_1 = tb_2, c_1 = tc_2$ impliquerait $t = 0).$ Cela r??sulte en trois dimensions depuis une seule ??quation lin??aire d??crit g??n??ralement un plan et une ligne est ce qui est commun ?? deux plans d'intersection distincts.

Equation vectorielle

L'??quation de vecteur de la ligne par les points A et B est donn??e par r = OA + λ AB (o?? λ est un scalaire).

Si un vecteur est OA et OB b est un vecteur, alors l'??quation de la ligne peut se ??crire: r = a + λ (b - a).

Un rayon ?? partir du point A est d??crite en limitant λ. Un rayon est obtenue si λ ≥ 0, et le rayon en face vient de λ ≤ 0.

Points align??s

Trois points sont dits ??tre colin??aire se ils se trouvent sur la m??me ligne. Dans l'espace euclidien , trois points d??terminent habituellement un plan , mais dans le cas de trois points align??s cela ne arrive pas.

Dans la g??om??trie des coordonn??es , dans l'espace de dimension n des points X = (x _1, x _2, ..., x _n), Y = (y _1, y _2, ..., y _n), et Z = (z _1, z _2, ..., z _n) sont align??s si la matrice

$\ Begin {} bmatrix 1 & x_1 & x_2 & \ & points x_n \\ 1 & y_1 & Y_2 & \ & points y_n \\ 1 & z_1 & Z_2 & \ & points z_n \ end {} bmatrix$

a un classer inf??rieur ?? 3. En particulier, pour trois points dans le plan (n = 2), ci-dessus matrice est carr??e et les points sont align??s si et seulement si son d??terminant est nul.

Lorsque la distance d (a, b) entre deux points A et B est d??fini, la colin??arit?? entre trois points peut ??tre exprim?? par:

Les points a, b et c sont align??s si et seulement si d (x, a) = d (c, a) et d (x, b) = d (c, b) implique x = c.

En g??om??trie euclidienne cette propri??t?? est vrai, car si c ne est pas sur la ligne d??termin??e par a et b, il y aura un autre point (pas ??gal ?? c) qui est tout aussi loin de a et b comme le point c est (visualiser le point de l'autre c??t?? de la ligne qui est l'image miroir de c).

Dans les g??om??tries o?? le concept d'une ligne est un notion primitive, comme peut ??tre le cas dans certains g??om??tries synth??tiques, d'autres m??thodes de d??termination de colin??arit?? sont n??cessaires.

Espace euclidien

Dans l'espace euclidien , R ⁿ (et analogue dans tous les autres espace affine), la ligne L passant par deux points diff??rents de A et B (consid??r?? comme vecteurs) est le sous-ensemble

$L = \ {(1-t) \, a + t \, b \ mi t \ in \ mathbb {R} \}$

La direction de la ligne est de a (t = 0) ?? b (t = 1), ou en d'autres termes, dans la direction du vecteur b - a. Diff??rents choix de A et B peuvent produire la m??me ligne.

Types de lignes

Dans un sens, toutes les lignes de la g??om??trie euclidienne sont ??gaux, en ce que, sans coordonn??es, on ne peut pas les distinguer les uns des autres. Cependant, les lignes peuvent jouer des r??les sp??ciaux par rapport ?? d'autres objets de la g??om??trie et ??tre divis?? en types selon cette relation. Par exemple, par rapport ?? une conique , les lignes peuvent ??tre:

lignes de Tangent ,
Droites s??cantes,
Lignes ext??rieures, qui ne satisfont pas la conique ?? tout point du plan euclidien, ou plus sp??cialis??es
directrice .

Pour plus g??n??ral courbes alg??briques, les lignes pourraient ??galement ??tre:

i -secant lignes, rencontrer la courbe aux points i compt?? sans la multiplicit??, ou
asymptotes.

En ce qui concerne triangles nous avons:

la Euler ligne, et
la Droites de Simson.

Pour un hexagone avec des sommets couch?? sur une conique nous avons la Pascal ligne et, dans le cas particulier o?? la conique est une paire de lignes, nous avons la ligne de Pappus.

La g??om??trie projective

Dans de nombreux mod??les de la g??om??trie projective, la repr??sentation d'une ligne rarement conforme ?? la notion de la ??courbe droite??, comme il est visualis?? dans la g??om??trie euclidienne. En G??om??trie elliptique nous voyons un exemple typique de cette. Dans la repr??sentation de la g??om??trie sph??rique elliptique, sont repr??sent??es par des lignes grands cercles de la sph??re avec des points diam??tralement oppos??s identifi??s. Dans un autre mod??le de g??om??trie elliptique, sont repr??sent??es par des lignes euclidiennes des plans passant par l'origine. M??me si ces repr??sentations sont visuellement distincts, ils r??pondent ?? toutes les propri??t??s (comme, deux points qui d??terminent une gamme unique) qui les rendent repr??sentations appropri??es pour lignes dans cette g??om??trie.

G??od??siques

Le "rectitude" d'une ligne, interpr??t?? comme la propri??t?? qu'il minimise les distances entre ses points, peut ??tre g??n??ralis??e et conduit ?? la notion de g??od??siques dans espaces m??triques.

R??cup??r?? ?? partir de " http://en.wikipedia.org/w/index.php?title=Line_(geometry)&oldid=548450546 "