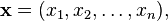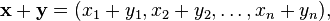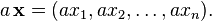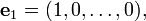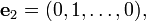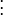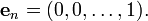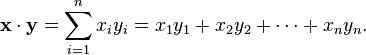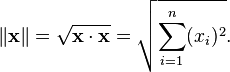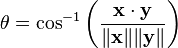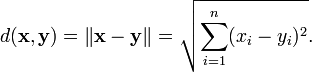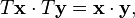Espace euclidien

Renseignements g??n??raux

SOS Enfants a fait cette s??lection Wikipedia aux c??t??s d'autres ??coles des ressources . Cliquez ici pour plus d'informations sur les enfants SOS.

Autour 300 BC , le grec math??maticien Euclide a entrepris une ??tude des relations entre les distances et les angles , d'abord dans un plan (une surface plane id??alis??e), puis dans l'espace. Un exemple d'une telle relation est que la somme des angles d'un triangle est toujours 180 degr??s. Aujourd'hui, ces relations sont connus comme deux et trois dimensions g??om??trie euclidienne .

Dans moderne math??matique langue, la distance et l'angle peuvent ??tre g??n??ralis??s facilement aux espaces de dimension 4, 5 dimensions, et m??me de dimensions sup??rieures. Un espace de dimension n avec les notions de distance et l'angle qui ob??issent aux relations euclidiennes est appel?? un espace de dimension euclidienne de n. La plupart de cet article est consacr??e au d??veloppement de la langue moderne n??cessaire pour le saut conceptuel ?? des dimensions sup??rieures.

Une propri??t?? essentielle d'un espace euclidien est sa plan??it??. Autres espaces existent dans la g??om??trie euclidienne qui ne sont pas. Par exemple, la surface d'une sph??re est pas; un triangle sur une sph??re (d??fini convenablement) aura des angles qui r??sument ?? quelque chose sup??rieur ?? 180 degr??s. En fait, il se agit essentiellement d'un seul espace euclidien de chaque dimension, alors qu'il ya de nombreux espaces non-euclidiennes de chaque dimension. Souvent, ces autres espaces sont construits en d??formant syst??matiquement espace euclidien.

Aper??u intuitive

Une fa??on de penser du plan euclidien est comme un ensemble de points satisfaisant certaines relations, exprimables en termes de distance et l'angle. Par exemple, il existe deux op??rations fondamentales de l'avion. Un est traduction, ce qui signifie un d??placement du plan de sorte que chaque point est d??cal?? dans le m??me sens et par la m??me distance. L'autre est rotation autour d'un point fixe dans le plan, dans lequel tous les points dans le plan tourne autour de ce point fixe du m??me angle. L'un des principes de base de la g??om??trie euclidienne est que deux chiffres (ce est- sous-ensembles ) du plan devraient ??tre consid??r??es comme ??quivalentes ( congruent) si l'on peut ??tre transform?? en l'autre par une s??quence de translations et des rotations. (Voir Groupe euclidien.)

Afin de rendre tout cela math??matiquement pr??cise, il faut d??finir clairement les notions de distance, l'angle, la traduction et la rotation. La m??thode standard pour ce faire, tel que r??alis?? dans le reste de cet article, est de d??finir le plan euclidien comme deux dimensions r??el espace vectoriel ??quip?? d'un produit interne. Car alors:

la des vecteurs dans l'espace de vecteur correspondent aux points du plan euclidien,
l' addition op??ration dans l'espace de vecteur correspond ?? la traduction, et
le produit scalaire implique notions d'angle et de distance, qui peuvent ??tre utilis??s pour d??finir rotation.

Une fois le plan euclidien a ??t?? d??crite dans cette langue, il est en fait une simple question d'??tendre son concept aux dimensions arbitraires. Pour la plupart, le vocabulaire, les formules et les calculs ne sont pas plus difficiles faites par la pr??sence de plusieurs dimensions. (Toutefois, les rotations sont plus subtiles dans les dimensions ??lev??es, et la visualisation des espaces de grande dimension reste difficile, m??me pour les math??maticiens exp??riment??s.)

Une ride finale est que l'espace euclidien ne est pas techniquement un espace vectoriel, mais plut??t une espace affine, sur lequel un espace vectoriel actes. Intuitivement, la distinction dit simplement qu'il n'y a pas le choix canonique de o?? le origine devrait aller dans l'espace, car il peut ??tre traduit partout. Dans cet article, cette technicit?? est largement ignor??.

R??el espace de coordonn??es

Soit R le champ de nombres r??els . Pour toute non-n??gative entier n, l'espace de tous les n - uplets de nombres r??els forme un espace vectoriel de dimension n sur R, qui est not??e R ⁿ et parfois appel?? r??el espace de coordonn??es. Un ??l??ment de R ⁿ est ??crit

$\ Mathbf {x} = (x 1, x_2, \ ldots, x_n),$

o?? chaque x _i est un nombre r??el. Les op??rations spatiales vectoriel sur R ⁿ sont d??finis par

$\ Mathbf {x} + \ mathbf {y} = (x 1 + y_1, x_2 + Y_2, \ ldots, x_n + y_n),$

$A \, \ mathbf {x} = (a x_1, un x_2, \ ldots, un x_n).$

L'espace vectoriel R ⁿ est livr?? avec un base standard:

$\ Mathbf {e} _1 = (1, 0, 0, \ ldots),$

$\ Mathbf {e} _2 = (0, 1, 0, \ ldots),$

$\ vdots$

$\ mathbf {e} _n = (0, 0, \ ldots, 1).$

Un vecteur arbitraire dans R ⁿ peut alors se ??crire sous la forme

$\ Mathbf {x} = \ sum_ {i = 1} ^ n x_i \ mathbf {e} _i.$

R ⁿ est l'exemple prototypique d'un espace vectoriel de dimension n r??elle. En fait, chaque r??elle n espace vectoriel de dimension V est isomorphe ?? R ^n. Ce ne est pas isomorphisme canonique, cependant. Un choix d'isomorphisme est ??quivalent ?? un choix de base de V (en regardant l'image de la norme de base pour R ⁿ en V). La raison pour travailler avec des espaces vectoriels arbitraires au lieu de R ⁿ est qu'il est souvent pr??f??rable de travailler d'une mani??re de coordonner-libre (ce est, sans choisir une base pr??f??r??e).

La structure euclidienne

Espace euclidien est plus que juste un v??ritable espace de coordonn??es. Afin d'appliquer la g??om??trie euclidienne, il faut ??tre en mesure de parler des distances entre les points et les angles entre les lignes ou des vecteurs. La voie naturelle pour obtenir ces grandeurs est en introduisant et en utilisant le produit scalaire standard (??galement connu sous le nom produit scalaire) sur R ^n. Le produit scalaire des deux vecteurs de x et y est d??fini par

$\ Mathbf {x} \ cdot \ mathbf {y} = \ sum_ {i = 1} ^ n = x_iy_i x_1y_1 + x_2y_2 + \ cdots + x_ny_n.$

Le r??sultat est toujours un nombre r??el. En outre, le produit scalaire de x par lui-m??me est toujours positif ou nul. Ce produit nous permet de d??finir la "longueur" d'un vecteur x comme

$\ | \ Mathbf {x} \ | = \ sqrt {\ mathbf {x} \ cdot \ mathbf {x}} = \ sqrt {\ sum_ {i = 1} ^ {n} (x_i) ^ 2}.$

Cette fonction de longueur satisfait les propri??t??s requises d'un norme et est appel??e la norme euclidienne de R ^n.

Le (non obtus) angle θ (0 ?? ≤ θ ≤ 180 ??) entre x et y est donn??e par

$\ Theta = \ cos ^ {- 1} \ left (\ frac {\ mathbf {x} \ cdot \ mathbf {y}} {\ | \ mathbf {x} \ | \ | \ mathbf {y} \ |} \ droite)$

o?? cos ^-1 est le arccosinus fonction.

Enfin, on peut utiliser la norme pour d??finir une m??trique (ou fonction de distance) sur R ⁿ par

$d (\ mathbf {x}, \ mathbf {y}) = \ | \ mathbf {x} - \ mathbf {y} \ | = \ sqrt {\ sum_ {i = 1} ^ n (x_i - y_i) ^ 2 }.$

Cette fonction de distance est appel??e M??trique euclidienne. Il peut ??tre consid??r?? comme une forme de th??or??me de Pythagore .

R??el espace de coordonn??es avec cette structure euclidienne est appel?? espace euclidien et souvent not??e E ^n. (De nombreux auteurs se r??f??rent ?? R ⁿ lui-m??me comme l'espace euclidien, avec la structure euclidienne ??tant entendu). La structure euclidienne E ⁿ fait un espace de produit int??rieur (en fait une Espace de Hilbert), un espace vectoriel norm??, et un espace m??trique.

Rotations de l'espace euclidien sont alors d??finis comme orientation de pr??servation lin??aire Transformations T qui pr??servent les angles et les longueurs:

$T \ mathbf {x} \ cdot T \ mathbf {y} = \ mathbf {x} \ cdot \ mathbf {y},$

$| T \ mathbf {x} | = | \ mathbf {x} |.$

Dans le langage des matrices , les rotations sont matrices orthogonales sp??ciales.

Topologie de l'espace euclidien

Depuis l'espace euclidien est un espace m??trique est ??galement un espace topologique avec le naturel topologie induit par l'indicateur. La topologie m??trique sur E ⁿ se appelle la topologie euclidienne. Un ensemble est ouverte dans la topologie euclidienne si et seulement se il contient un boule ouverte autour de chacun de ses points. La topologie euclidienne se av??re ??tre l'??quivalent de la topologie produit sur R ⁿ consid??r?? comme un produit de n copies de la droite r??elle R (avec sa topologie standard).

Un r??sultat important de la topologie de R ^n, qui est loin d'??tre superficielle, est Brouwer invariance de domaine. Tout sous-ensemble de R ⁿ (avec son Topologie induite) ce est hom??omorphe ?? un autre sous-ensemble ouvert de R ⁿ est elle-m??me ouverte. Une cons??quence imm??diate est que R ^m ne est pas hom??omorphe ?? R ⁿ si m ≠ n - un intuitivement "??vidente" r??sultat qui est n??anmoins difficile ?? prouver.

G??n??ralisations

En math??matiques modernes, espaces euclidiens forment les prototypes pour d'autres, des objets g??om??triques plus complexes. Par exemple, un vari??t?? lisse est un S??par?? de l'espace topologique qui est localement diff??omorphe ?? l'espace euclidien. Diff??omorphisme ne respecte pas la distance et l'angle, de sorte que ces concepts cl??s de la g??om??trie euclidienne est perdu sur une vari??t?? lisse. Toutefois, si l'on prescrit en outre un produit scalaire variant doucement sur le collecteur de espaces tangents, alors le r??sultat est ce qu'on appelle une Vari??t?? riemannienne. Autrement dit, une vari??t?? riemannienne est un espace construit par d??formation et recollant espaces euclidiens. Tel espace b??n??ficie notions de distance et l'angle, mais ils se comportent dans un incurv??e de mani??re, non-euclidienne. Le plus simple vari??t?? riemannienne, constitu?? de R ⁿ avec un produit int??rieur constant, est essentiellement identique ?? euclidiens n se -Espace.

Si l'on modifie un espace euclidien de sorte que son produit interne devient n??gatif dans une ou plusieurs directions, puis le r??sultat est un l'espace pseudo-euclidien. Vari??t??s lisses construites ?? partir de ces espaces sont appel??s collecteurs de pseudo-riemannienne. Peut-??tre leur application la plus c??l??bre est la th??orie de la relativit?? , o?? vide espace-temps sans question est repr??sent?? par l'espace pseudo-euclidien plat appel?? L'espace de Minkowski, espaces-temps avec de la mati??re dans les autres forment des collecteurs pseudo-riemannien, et la gravit?? correspondant ?? la courbure d'un tel collecteur.

Notre univers, ??tre soumis ?? la relativit??, ne est pas euclidienne. Cela devient important dans des consid??rations th??oriques de l'astronomie et de la cosmologie , et aussi dans certains probl??mes pratiques tels que positionnement global et avion la navigation. N??anmoins, un mod??le euclidien de l'univers peut encore ??tre utilis?? pour r??soudre de nombreux autres probl??mes pratiques avec une pr??cision suffisante.

R??cup??r?? ?? partir de " http://en.wikipedia.org/w/index.php?title=Euclidean_space&oldid=196930203 "