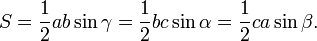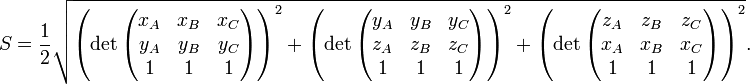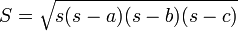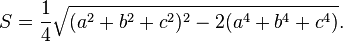Triangle

Contexte des ??coles Wikip??dia

Enfants SOS ont produit une s??lection d'articles de wikipedia pour les ??coles depuis 2005. parrainage SOS enfant est cool!

Un triangle est une base de la formes de la g??om??trie : un polygone avec trois coins ou sommets et trois c??t??s ou des bords qui sont des segments de ligne.

En g??om??trie euclidienne trois quelconques non points align??s d??terminent un triangle unique et un cadre unique plan (ce est ?? dire en deux dimensions espace cart??sien ).

Un triangle.

Types de triangles

Triangles peuvent ??tre class??s en fonction de la longueur relative de leurs c??t??s:

Dans un triangle ??quilat??ral, tous les c??t??s sont de longueur ??gale. Un triangle ??quilat??ral est aussi un polygone ??quiangles, ce est ?? dire tous ses internes angles sont ??gaux, ?? savoir 60 ??; c'est un polygone r??gulier.
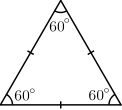
Dans un triangle isoc??le, les deux c??t??s sont de m??me longueur (?? l'origine et classiquement limit??e ?? exactement deux). Un triangle isoc??le a aussi deux angles ??gaux: les angles oppos??s aux deux c??t??s ??gaux.
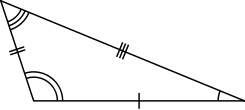
Dans un triangle scal??ne, tous les c??t??s ont des longueurs diff??rentes. Les angles internes dans un triangle scal??ne sont tous diff??rents.


??quilat??ral	Isoc??le	Scal??ne

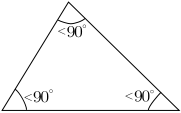
Triangles peuvent ??galement ??tre class??s en fonction de leurs angles internes, d??crites ci-dessous ?? l'aide degr??s d'arc:

Un triangle (ou triangle rectangle, anciennement appel?? un triangle rectangled) a une angle de 90 ?? interne ( ?? angle droit ). Le c??t?? oppos?? ?? l'angle droit est le hypot??nuse; ce est le c??t?? le plus long dans le triangle rectangle. Les deux autres c??t??s sont les jambes ou catheti (singulier: angle droit) du triangle.
Un triangle oblique n'a pas angle interne ??gale ?? 90 ??.
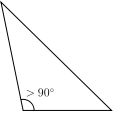
Un triangle est un triangle obtus oblique avec une angle interne sup??rieur ?? 90 ?? (un angle d'obtus ).
Un triangle est un triangle aigu oblique par tous les angles internes plus petits que 90 ?? (trois angles aigus ). Un triangle ??quilat??ral est un triangle aigu??, mais pas tous les triangles aigus sont des triangles ??quilat??raux.


Droit	Obtus	Aigu
	$\ Underbrace {\ qquad \ qquad \ qquad \ qquad \ qquad \ qquad} _ {}$
	Oblique

Donn??es de base

Faits ??l??mentaires sur triangles ont ??t?? pr??sent??s par Euclide dans les livres 1-4 de ses ??l??ments autour 300 BCE. Un triangle est un polygone et un 2- simplex (voir polytope). Tous deux sont des triangles dimensionnelle.

Les angles d'un triangle se additionnent ?? 180 degr??s. Une angle ext??rieur d'un triangle (un angle qui est adjacent et compl??mentaire ?? un angle interne) est toujours ??gale ?? deux angles d'un triangle qui ne est pas adjacent / compl??mentaire ??. Comme tous de polygone convexe, les angles ext??rieurs d'un triangle se additionnent ?? 360 degr??s.

La somme des longueurs de tous les deux c??t??s d'un triangle est toujours sup??rieure ?? la longueur du troisi??me c??t??. Ce est la in??galit?? triangulaire. (Dans le cas particulier de l'??galit??, deux des angles se sont effondr??s ?? la taille z??ro, et le triangle a d??g??n??r?? ?? un segment de ligne.)

Deux triangles sont dits similaire si et seulement si les angles de celui-ci sont ??gaux aux angles correspondants de l'autre. Dans ce cas, les longueurs de leurs c??t??s correspondants sont proportionnelle. Cela se produit par exemple lorsque deux triangles part un angle et les c??t??s oppos??s ?? cet angle sont parall??les.

A quelques postulats et les th??or??mes de base sur les triangles semblables:

Deux triangles sont semblables si au moins deux angles correspondants sont ??gaux.
Si les deux faces correspondantes de deux triangles sont en proportion, et leurs angles inclus sont ??gaux, les triangles sont semblables.
Si trois c??t??s de deux triangles sont en proportion, les triangles sont semblables.

Pour deux triangles pour ??tre en harmonie, chacun de leurs angles et les c??t??s correspondant doit ??tre ??gale (6 au total). A quelques postulats et les th??or??mes de base sur triangles congruents:

SAS Postulat: Si deux c??t??s et les angles inclus de deux triangles sont proportionnellement ??gale, les deux triangles sont congruents.
SSS Postulat: Si chaque c??t?? de deux triangles sont ??gaux en cons??quence, les triangles sont congruents.
ASA Postulat: Si deux angles et les c??t??s inclus de deux triangles sont proportionnellement ??gale, les deux triangles sont congruents.
AAS Th??or??me: Si deux angles et ne importe quel c??t?? de deux triangles sont proportionnellement ??gale, les deux triangles sont congruents.
Hypotenuse-Leg Th??or??me: Si les hypot??nuses et une jambe de deux triangles rectangles sont proportionnellement ??gale, les triangles sont congruents.

Utilisation des triangles rectangles et la notion de similitude, l' fonctions trigonom??triques sinus et cosinus peuvent ??tre d??finis. Ce sont des fonctions d'un angle qui sont ??tudi??e dans la trigonom??trie .

En g??om??trie euclidienne, la somme des angles int??rieurs d'un triangle est ??gal ?? 180 ??. Ceci permet la d??termination de la troisi??me angle d'un triangle, d??s que deux angles sont connus.

Le th??or??me de Pythagore

Un th??or??me central est le th??or??me de Pythagore , qui indique dans un triangle rectangle, le carr?? de la longueur de la hypot??nuse est ??gal ?? la somme des carr??s des longueurs des deux autres c??t??s. Si l'hypot??nuse a une longueur c, et les jambes ont des longueurs A et B, puis les Etats th??or??me

$a ^ 2 + b ^ 2 = c ^ 2 \,$

L'inverse est vrai: si les longueurs des c??t??s d'un triangle satisfont ?? l'??quation ci-dessus, alors le triangle est un triangle rectangle.

Certains autres faits sur des triangles rectangles:

Les angles aigus d'un triangle rectangle sont compl??mentaire.
Si les jambes d'un triangle rectangle sont ??gaux, alors les angles oppos??s des jambes sont ??gales, aigu?? et compl??mentaire, et ainsi sont ?? la fois 45 degr??s. D'apr??s le th??or??me de Pythagore, la longueur de l'hypot??nuse est la racine carr??e de deux fois la longueur d'une jambe.
Dans un triangle rectangle 30 ?? 60, dans lequel les angles aigus mesure 30 et 60 degr??s, l'hypot??nuse est deux fois la longueur du c??t?? le plus court.
Dans tous les triangles rectangles, sur la m??diane de l'hypot??nuse est la moiti?? de l'hypot??nuse.

Pour tous les triangles, les angles et les c??t??s sont reli??s par la loi des cosinus et loi des sinus.

Points, lignes et cercles associ??s ?? un triangle

Il ya des centaines de diff??rentes constructions qui trouvent un point sp??cial ?? l'int??rieur d'un triangle, satisfaisant une certaine propri??t?? unique: voir la section des r??f??rences pour un catalogue d'entre eux. Souvent, ils sont construits en trouvant trois lignes associ??es de fa??on sym??trique avec les trois c??t??s (ou sommets) et ensuite prouver que les trois lignes se rencontrent en un point unique: un outil important pour prouver l'existence de ceux-ci est Le th??or??me de Ceva, ce qui donne un crit??re pour d??terminer quand ces trois lignes sont concurrente. De m??me, les lignes associ??es ?? un triangle sont souvent construits en prouvant que trois points sym??triquement construits sont colin??aires: ici Th??or??me de M??n??la??s donne un crit??re g??n??ral utile. Dans cette section, quelques-unes des constructions les plus couramment rencontr??s sont expliqu??s-.

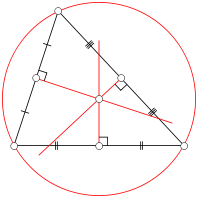
Le cercle circonscrit est le centre d'un cercle passant par les trois sommets du triangle.

Un m??diatrice d'un triangle est une ligne droite passant par le point milieu d'un c??t?? et ??tant perpendiculaire ?? elle, ce est ?? dire formant un angle droit avec elle. Les trois m??diatrices se rencontrent en un point unique, de triangle circonscrit; ce point est le centre de la cercle circonscrit, le cercle passant par les trois sommets. Le diam??tre de ce cercle peut ??tre trouv?? dans la loi des sinus indiqu?? ci-dessus.

Le th??or??me de Thales implique que si le centre du cercle circonscrit est situ?? sur un c??t?? du triangle, l'angle oppos?? est bonne. Plus, ce est vrai: si le cercle circonscrit est situ?? ?? l'int??rieur du triangle, le triangle est aigu??; si le cercle circonscrit est situ?? en dehors du triangle, alors le triangle est obtus.

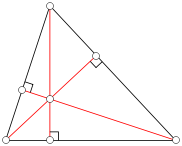
L'intersection des courbes est le orthocentre.

Une L'altitude d'un triangle est une ligne droite passant par un sommet et perpendiculaire (ce est ?? dire formant un angle droit avec) du c??t?? oppos??. Ceci est appel?? c??t?? oppos?? de la base de l'altitude, et le point o?? l'altitude coupe la base (ou son prolongement) est appel??e pied de l'altitude. La longueur de l'altitude est la distance entre la base et le sommet. Les trois courbes se coupent en un point unique, appel?? le orthocentre du triangle. Le orthocenter se trouve ?? l'int??rieur du triangle si et seulement si le triangle est aigu. Les trois sommets ensemble avec l'orthocentre sont dits pour former un orthocentrique syst??me.

L'intersection des bissectrices calcule le centre de la incircle.

Une bissectrice d'un triangle est une ligne droite passant par un sommet qui coupe l'angle correspondant ?? la moiti??. Les trois bissectrices se coupent en un seul point, la incenter, le centre du triangle de incircle. Le cercle inscrit est le cercle qui se trouve ?? l'int??rieur du triangle et touche tous les trois c??t??s. Il ya trois autres cercles importants, le exinscrits; ils se trouvent ?? l'ext??rieur du triangle et touchent un c??t?? ainsi que les prolongements des deux autres. Les centres des entr??es et exinscrits forment un orthocentrique syst??me.

Le barycentre est le centre de gravit??.

Un m??diane d'un triangle est une ligne droite passant par un sommet et le point m??dian du c??t?? oppos?? et divise le triangle en deux parties ??gales. Les trois m??dianes se coupent en un point unique, le triangle de centre de gravit??. Ce est aussi du triangle du centre de gravit?? : si le triangle ont ??t?? faite de bois, par exemple, vous pourriez en ??quilibre sur son centre de gravit??, ou sur une ligne ?? travers le centre de gravit??. Le centro??de chaque coupe m??diane dans le rapport 2: 1, ce est ?? dire la distance entre un sommet et le centre de gravit?? est deux fois plus grande que la distance entre le centre de gravit?? et le point milieu du c??t?? oppos??.

Cercle d'Euler d??montre une sym??trie o?? six points se trouvent sur le bord du triangle.

Les milieux des trois c??t??s et les pieds des trois courbes se situent tous sur un m??me cercle, le triangle de Cercle d'Euler. Les trois autres points pour lesquels il est nomm?? sont les milieux de la partie d'altitude entre les sommets et la orthocentre. Le rayon du cercle de neuf points est la moiti?? de celui du cercle circonscrit. Il touche le cercle inscrit (au Point de Feuerbach) et les trois exinscrits.

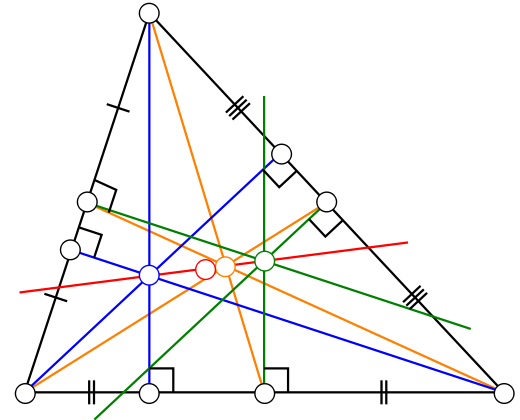
La ligne d'Euler est une droite passant par le centre de gravit?? (orange), orthocentre (bleu), circonscrit (vert) et le centre du cercle de neuf points (rouge).

Le centre de gravit?? (jaune), orthocentre (bleu), circonscrit (vert) et barycentre du Cercle d'Euler (point rouge) se trouvent tous sur une seule ligne, connue sous le nom La ligne d'Euler (ligne rouge). Le centre du cercle de neuf points se situe ?? mi-chemin entre l'orthocentre et le cercle circonscrit, et la distance entre le centre de gravit?? et le cercle circonscrit est la moiti?? de celle entre le centre et l'orthocentre.

Le centre du cercle inscrit ne est pas en g??n??ral situ?? sur la ligne d'Euler.

Si l'on r??fl??chit une m??diane ?? la bissectrice de l'angle qui passe par le m??me sommet, on obtient un Sym??diane. Les trois symmedians se croisent en un seul point, le Point Sym??diane du triangle.

Calcul de l'aire d'un triangle

Calcul de l'aire d'un triangle est un probl??me rencontr?? fr??quemment ??l??mentaire dans de nombreuses situations diff??rentes. La formule la plus connue et la plus simple est

$S = \ frac {1} {2} bh$

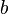o?? $S$ est la zone, $b$ est la longueur de la base du triangle, et $h$ est la hauteur ou l'altitude du triangle. Le terme ??base?? d??signe ne importe quel c??t??, et "hauteur" d??signe la longueur d'une perpendiculaire ?? l'oppos?? de la face sur la face elle-m??me.

Bien que simple, cette formule ne est utile que si la hauteur peut ??tre facilement trouv??. Par exemple, l'arpenteur d'un champ triangulaire mesure la longueur de chaque c??t??, et peut trouver la zone de ses r??sultats sans avoir ?? construire un 'height'. Divers proc??d??s peuvent ??tre utilis??s dans la pratique, en fonction de ce qui est connu au sujet du triangle. Ce qui suit est une s??lection de formules fr??quemment utilis??es pour l'aire d'un triangle.

Utilisation de vecteurs

L'aire d'un parall??logramme peut ??tre calcul?? en utilisant des vecteurs . Laissez vecteurs AB et AC respectivement le point de A ?? B et de A ?? C. La zone de parall??logramme ABCD est alors | AB ?? AC |, qui est l'ampleur du produit crois?? de vecteurs AB et AC. | AB ?? AC | est ??gal ?? | h ?? AC |, o?? h repr??sente l'altitude h comme vecteur.

L'aire du triangle ABC est la moiti??, ou S = ?? | AB ?? AC |.

L'aire du triangle ABC peut ??galement ??tre exprim?? en terme de produits scalaires comme suit:

$\ Frac {1} {2} \ sqrt {(\ mathbf {AB} \ cdot \ mathbf {AB}) (\ mathbf {AC} \ cdot \ mathbf {} AC) - (\ mathbf {AB} \ cdot \ mathbf {} AC) ^ 2} = \ frac {1} {2} \ sqrt {| \ mathbf {AB} | ^ 2 | \ mathbf {AC} | ^ 2 - (\ mathbf {AB} \ cdot \ mathbf {AC }) ^ 2} \,.$

Application de la trigonom??trie pour trouver l'altitude h.

Utiliser la trigonom??trie

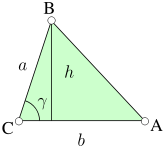
La hauteur d'un triangle peut ??tre trouv?? par l'application de la trigonom??trie . Utilisation de l'??tiquetage comme dans l'image sur la gauche, l'altitude est un p??ch?? h = γ. En substituant cette dans la formule S = ?? bh d??riv??e ci-dessus, la surface du triangle peut ??tre exprim??e comme:

$S = \ frac {1} {2} ab \ sin \ gamma = \ frac {1} {2} bc \ sin \ alpha = \ frac {1} {2} ca \ sin \ beta.$

En outre, puisque le p??ch?? α = sin (π - α) = sin (β + γ), et de m??me pour les deux autres angles:

$S = \ frac {1} {2} ab \ sin (\ alpha + \ beta) = \ frac {1} {2} bc \ sin (\ beta + \ gamma) = \ frac {1} {2} ca \ sin ( \ gamma + \ alpha).$

Utilisation de coordonn??es

Si le sommet A est situ?? ?? l'origine (0, 0) d'un syst??me de coordonn??es cart??siennes et les coordonn??es des deux autres sommets sont donn??s par B = (x _B, y _B) et C = _(C x, y _C), puis la surface S peut ??tre calcul?? comme une fois et demie la valeur absolue du d??terminant

$S = \ frac {1} {2} \ left | \ det \ begin {} pmatrix X_B & x_C \\ y_B & y_C \ end {pmatrix} \ right | = \ frac {1} {2} | X_B y_C - x_C y_B |.$

Pour les trois sommets g??n??raux, l'??quation est la suivante:

$S = \ frac {1} {2} \ left | \ det \ begin {} pmatrix x_A & X_B & x_C \\ ??_?? & y_B & y_C \\ 1 & 1 & 1 \ end {pmatrix} \ right | = \ frac {1} {2} \ big | x_A y_C - x_A y_B + X_B ??_?? - X_B y_C + x_C y_B - x_C ??_?? \ big |.$

En trois dimensions, la surface d'un triangle g??n??rale {A = (x _A, y _A, z _A), B = (x _B, y _B, z _B) et C = _(C x, _C y, z _C)} est le Pythagore somme des aires des projections respectives sur les trois plans principaux (ce est ?? dire x = 0, y = 0 et z = 0):

$S = \ frac {1} {2} \ sqrt {\ left (\ det \ begin {} pmatrix x_A & X_B & x_C \\ ??_?? & y_B & y_C \\ 1 & 1 & 1 \ end {pmatrix} \ droite) ^ 2 + \ left (\ det \ begin {} pmatrix ??_?? & y_B & y_C \\ Z_A & z_B & z_C \\ 1 & 1 & 1 \ end {} pmatrix \ right) ^ 2 + \ left (\ det \ begin {} pmatrix Z_A & z_B & z_C \\ x_A & X_B & x_C \\ 1 & 1 & 1 \ end {} pmatrix \ right) ^ 2}.$

En utilisant la formule de H??ron

La forme du triangle est d??termin??e par les longueurs des c??t??s seulement. Par cons??quent, la surface S peut ??galement ??tre d??riv??e ?? partir des longueurs des c??t??s. Par La formule de H??ron:

$S = \ sqrt {s (s-a) (S-B) (s-c)}$

o?? s = ?? (a + b + c) est le demi-p??rim??tre, ou la moiti?? du p??rim??tre du triangle.

Une fa??on ??quivalente de la r??daction de la formule de H??ron est

$S = \ frac {1} {4} \ sqrt {(a ^ 2 + b ^ 2 + c ^ 2) ^ 2-2 (a + b ^ 4 ^ 4 + c ^ 4)}.$

Triangles non-planaires

Un triangle non plane est un triangle qui ne est pas contenu dans un (plat) avion. Des exemples de triangles non planes dans des g??om??tries non-euclidienne sont triangles sph??riques en g??om??trie sph??rique et triangles hyperboliques g??om??trie hyperbolique.

Bien que tous r??guli??re, deux dimensions planes (triangles) contiennent des angles qui se ajoutent ?? 180 ??, il existe des cas dans lesquels les angles d'un triangle peut ??tre sup??rieur ou inf??rieur ?? 180 ??. En chiffres courbes, un triangle sur une figure ?? courbure n??gative ("selle") aura ses angles ajouter jusqu'?? moins de 180 ?? tandis qu'un triangle sur un chiffre courbure positive ("sph??re") aura ses angles se additionnent ?? plus de 180 ??. Ainsi, si l'on devait dessiner un triangle g??ant sur la surface de la Terre, on constaterait que la somme de ses angles ??taient sup??rieures ?? 180 ??.

R??cup??r?? ?? partir de " http://en.wikipedia.org/w/index.php?title=Triangle&oldid=199244337 "