
Polygone
Renseignements g??n??raux
Cette s??lection se fait pour les ??coles par la charit?? pour enfants lire la suite . Tous les enfants disponibles pour le parrainage de SOS Enfants des enfants sont pris en charge dans une maison de famille pr??s de la charit??. Lire la suite ...

Dans la g??om??trie d'un polygone (pron .: / p ɒ l ɪ ɡ ɒ n /) Est une forme plane constitu??e de lignes droites qui sont joints pour former un cha??ne ou circuit ferm??.
Un polygone est traditionnellement un plan chiffre qui est d??limit?? par une fermeture chemin, compos?? d'une suite finie de droite segments de ligne (ce est ?? dire, par un cha??ne polygonale ferm??e). Ces segments sont appel??s ses bords ou sur les c??t??s, et les points o?? deux bords rencontrent sont les sommets du polygone (singulier: sommet) ou des coins. Un n-gon est un polygone ?? n c??t??s. L'int??rieur du polygone est parfois appel?? son corps. Un polygone est un exemple deux dimensions de la plus g??n??rale polytope dans un nombre quelconque de dimensions.
Le mot ??polygone?? d??rive du grec πολύς (Polus) "beaucoup", "beaucoup" et γωνία (Goni??) "coin", "angle", ou γόνυ (Gonu) "genou".
La notion g??om??trique de base a ??t?? adapt?? de diverses mani??res pour r??pondre ?? des fins particuli??res. Les math??maticiens sont souvent pr??occup??s seulement avec la cha??ne polygonale ferm??e et polygones simples qui ne sont pas auto-intersection, et peut d??finir un polygone cons??quence. G??om??triquement r??union de deux bords ?? un coin sont n??cessaires pour former un angle qui ne est pas droit (180 ??); autrement, les segments de ligne seront consid??r??es comme des parties d'un seul bord; Mais math??matiquement, ces coins peuvent parfois ??tre autoris??s. Dans les domaines relatifs au calcul, le polygone terme a pris un sens l??g??rement modifi?? d??riv?? de la fa??on dont la forme est stock?? et manipul?? en infographie (g??n??ration d'image). Certains autres g??n??ralisations de polygones sont d??crits ci-dessous.
Classification

Nombre de c??t??s
Les polygones sont essentiellement class??s par le nombre de c??t??s. Voir tableau ci-dessous .
Convexit?? et les types de non-convexit??
Les polygones peuvent ??tre caract??ris??s par leur convexit?? ou le type de non-convexit??:
- Convex: toute ligne trac??e ?? travers le polygone (et non tangent ?? un bord ou coin) rencontre sa limite exactement deux fois. De mani??re ??quivalente, tous ses angles internes sont inf??rieurs ?? 180 ??.
- Non-convexe: une ligne peut ??tre trouv?? qui r??pond ?? sa fronti??re plus de deux fois. En d'autres termes, il contient au moins un angle int??rieur avec une mesure plus grande que 180 ??.
- Simple: la limite du polygone ne se croisent pas. Tous les polygones convexes sont simples.
- Concave: non-convexe et simple.
- Star-forme: tout l'int??rieur est visible ?? partir d'un seul point, sans traverser ne importe quel bord. Le polygone doit ??tre simple, et peut ??tre convexe ou concave.
- Auto-intersection: la limite du polygone traverse elle-m??me. Branko Gr??nbaum appelle ces copte, bien que ce terme ne semble pas ??tre largement utilis??. Le complexe de terme est parfois utilis?? ?? la diff??rence de simple, mais cet usage risque de confusion avec l'id??e d'un polygone complexe que celle qui existe dans le complexe Hilbert plan constitu?? par les deux complexes dimensions.
- ??toile polygone: un polygone qui se auto-intersecte de fa??on r??guli??re.
Sym??trie
- ??quiangles: tous ses angles de coin sont ??gaux.
- Cycliques: tous les coins se situent sur un seul cercle .
- Isogonal ou sommet-transitif: tous les coins se situent dans la m??me sym??trie orbite. Le polygone est ??galement cyclique et ??quiangulaire.
- ??quilat??raux: toutes les ar??tes sont de m??me longueur. (Un polygone ?? cinq c??t??s ou plus peut ??tre ??quilat??ral sans ??tre convexe.)
- Isotoxal ou Edge-transitif: tous les c??t??s se trouvent dans le m??me sym??trie orbite. Le polygone est ??quilat??ral.
- Tangentielle: tous les c??t??s sont tangents ?? un cercle inscrit.
- Normal: Un polygone est r??gulier se il est ?? la fois cyclique et ??quilat??ral. Un polygone r??gulier non-convexe est appel?? r??guli??re polygone ??toiles.
Propri??t??s
La g??om??trie euclidienne est suppos?? dans l'ensemble.
Angles
Tout polygone, auto-intersection r??guli??re ou irr??guli??re ou simple, a autant de coins comme il a des c??t??s. Chaque coin a plusieurs angles. Les deux plus importants sont:
- Angle int??rieur - La somme des angles int??rieurs d'un n-gon est simple, (n - 2) π radians ou (N - 2) 180 degr??s . Ce est parce que tout n -gon simple peut ??tre consid??r?? comme constitu?? de (n - 2) triangles, dont chacun a un angle somme de π radians ou 180 degr??s. La mesure de ne importe quel angle int??rieur d'un convexe r??guli??re n-gon est
 radians ou
radians ou  degr??s. Les angles int??rieurs d'r??guli??re polygones ??toil??s ont ??t?? ??tudi??s par Poinsot, dans le m??me journal dans lequel il d??crit les quatre poly??dres r??guliers ??toiles.
degr??s. Les angles int??rieurs d'r??guli??re polygones ??toil??s ont ??t?? ??tudi??s par Poinsot, dans le m??me journal dans lequel il d??crit les quatre poly??dres r??guliers ??toiles.
- Angle ext??rieur - Tracing autour d'un n-gon convexe, l'angle "tourn??" ?? un coin est l'angle ext??rieur ou externe. Tracing tout le chemin autour du polygone fait un tour complet tourner, de sorte que la somme des angles ext??rieurs doit ??tre de 360 ??. Cet argument peut ??tre g??n??ralis??e ?? concave polygones simples, si angles externes qui tournent dans le sens oppos?? sont soustraites du total tourn??. Tra??age autour d'un n-gone, en g??n??ral, la somme des angles ext??rieurs (la quantit?? totale tourne ?? une sommets) peut ??tre ne importe quel nombre entier d multiple de 360 ??, par exemple 720 ?? pour un pentagone et 0 ?? pour un angle "huit", o?? d est la densit?? ou starriness du polygone. Voir ??galement en orbite (dynamique).
L'angle ext??rieur est le angle suppl??mentaire ?? l'angle int??rieur. De ce la somme des angles int??rieurs peut ??tre facilement confirm??, m??me si certains angles int??rieurs sont plus de 180 ??: dans le sens horaire autour, cela signifie que l'on parfois tourne ?? gauche au lieu de droite, qui est consid??r?? comme tourner un montant n??gatif. (Nous consid??rons donc quelque chose comme le num??ro de l'orientation des c??t??s, o?? ?? chaque sommet de la contribution est entre la liquidation -. 1/2 et 1/2 d'enroulement)
R??gion et centre de gravit??

La surface d'un polygone est la mesure de la r??gion de dimension 2 d??limit??e par le polygone. Pour un non-auto-intersection ( simples polygone) ?? n sommets, la r??gion et centro??de sont donn??es par:
Pour fermer le polygone, le premier et le dernier sommets sont les m??mes, ce est ?? dire, x n, y n = x 0, y 0. Les sommets doivent ??tre class??s en fonction de l'orientation positive ou n??gative (?? gauche ou ?? droite, respectivement); si elles sont ordonn??es n??gativement, la valeur donn??e par la formule de la zone sera n??gatif, mais correct dans valeur absolue , mais le calcul 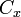 et
et 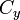 , La valeur sign??e de
, La valeur sign??e de  (Qui dans ce cas est n??gative) doit ??tre utilis??. Ceci est commun??ment appel?? le Formule de l'arpenteur.
(Qui dans ce cas est n??gative) doit ??tre utilis??. Ceci est commun??ment appel?? le Formule de l'arpenteur.
La formule de zone est calcul?? en prenant chaque ar??te AB, et en calculant le (sign??) ABO aire du triangle avec un sommet ?? l'origine O, en prenant le produit crois?? (qui donne ?? l'aire d'un parall??logramme) et en divisant par 2. Comme une se enroule autour du polygone, ces triangles avec zone positive et n??gative se chevauchent, et les zones entre l'origine et le polygone seront annul??s et r??sumer ?? 0, tandis que seule la zone ?? l'int??rieur du triangle de r??f??rence reste. Ce est pourquoi la formule est appel??e la formule de l'arpenteur, depuis le ??arpenteur?? est ?? l'origine; si vous allez dans le sens antihoraire, zone positive est ajout?? en allant de gauche ?? droite et la zone n??gative est ajout?? en allant de droite ?? gauche, du point de vue de l'origine.
La formule a ??t?? d??crit par Meister en 1769 et par Gauss en 1795. Il peut ??tre v??rifi??e en divisant le polygone en triangles, mais elle peut aussi ??tre consid??r??e comme un cas particulier de Le th??or??me de Green.
La zone A d'un polygone simple, peut ??galement ??tre calcul??e si les longueurs des c??t??s, a 1, a 2, ..., a n et la angles ext??rieurs, θ 1, θ 2, ..., θ n sont connus. La formule est la
La formule a ??t?? d??crit par Lopshits en 1963.
Si le polygone peut ??tre dessin?? sur une grille r??guli??rement espac??s de telle sorte que tous les sommets sont les points de grille, Th??or??me de Pick donne une formule simple pour la zone du polygone bas??e sur le nombre de points de grille int??rieur et aux limites.
Dans chaque polygone ?? p??rim??tre p et la zone A, le l'in??galit?? isop??rim??trique  d??tient.
d??tient.
Si deux polygones simples de m??me aire sont donn??s, le premier peut ??tre coup?? en morceaux polygonaux qui peuvent ??tre r??assembl??s pour former le deuxi??me polygone. Ceci est le Th??or??me Bolyai-Gerwien.
L'aire d'un polygone r??gulier est ??galement donn??e en termes de rayon r de son cercle inscrit et par son p??rim??tre p
 .
.
Ce rayon est ??galement appel?? son apoth??me et est souvent repr??sent?? comme un.
L'aire d'un n-gon r??gulier avec le c??t?? inscrit dans un cercle unit?? est
 .
.
L'aire d'un n-gon r??guli??re en termes de rayon r de son cercle circonscrit et son p??rim??tre p est donn??e par
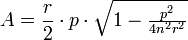 .
.
L'aire d'un n-gon r??gulier, inscrit dans un cercle de rayon unit??, avec le c??t?? s et l'angle θ int??rieur peut aussi ??tre exprim??e comme trigonom??triquement
 .
.
Les c??t??s d'un polygone ne le font pas, en g??n??ral d??terminer la zone. Cependant, si le polygone est cyclique les c??t??s font d??terminer la zone. De tous c??t??s avec n -gons donn??s, celui avec la plus grande zone est cyclique. De tous les n -gons avec un p??rim??tre donn??, celui avec la plus grande zone est r??gulier (et donc cyclique).
polygones auto-intersection
L'aire d'un polygone de l'auto-intersection peut ??tre d??finie de deux mani??res diff??rentes, dont chacune donne une r??ponse diff??rente:
- En utilisant les proc??d??s ci-dessus pour les polygones simples, on d??couvre que des r??gions particuli??res ?? l'int??rieur du polygone peuvent avoir leur surface multipli??e par un facteur que l'on appelle la densit?? de la r??gion. Par exemple, le pentagone convexe centrale dans le centre d'un pentagone a une densit?? 2. Les deux r??gions triangulaires d'un quadrilat??re en coupe (comme une figure 8) oppos??s ont des densit??s-sign??, et l'addition de leurs zones ensemble, peuvent donner une surface totale de z??ro pour la figure enti??re.
- Consid??rant les r??gions clos que des ensembles de points, nous pouvons trouver la zone de l'ensemble de points clos. Cela correspond ?? la zone du plan couvert par le polygone, ou ?? la surface d'un polygone simple ayant le m??me contour que l'auto-coupant une (ou, dans le cas de la traverse quadrilat??re, les deux triangles simples).
Degr??s de libert??
Un n-gon a 2 n degr??s de libert??, y compris pour la position 2, pour une orientation de rotation, et pour une taille globale, de sorte que 2 n - 4 pour fa??onner. Dans le cas d'un ligne de sym??trie ce dernier se r??duit ?? n - 2.
Soit k ≥ 2 Pour une nk -gon avec k -fois sym??trie de rotation (C k), il ya deux n -. 2 degr??s de libert?? pour la forme. Avec miroir image suppl??mentaire sym??trie (D k) il ya n - 1 degr??s de libert??.
Produit de distances ?? partir d'un sommet ?? d'autres sommets d'un polygone r??gulier
Pour un n-gon r??gulier inscrit dans un cercle de rayon unit??, le produit de la distance entre un sommet donn?? ?? tous les autres sommets est ??gal ?? n.
G??n??ralisations de polygones
Dans un sens large, un polygone est une (sans extr??mit??s) s??quence ou circuit de segments alternant (c??t??s) et les angles (angles) sans limite. Un polygone ordinaire est illimit??e parce que la s??quence se referme en elle-m??me dans une boucle ou un circuit, tandis qu'un apeirogon (du polygone infini) est illimit??e, car il va ?? l'infini. La compr??hension math??matique moderne est de d??crire une telle s??quence structurelle en termes de " polygone abstrait ", qui est un partiellement ordonn?? set (ensemble ordonn??) des ??l??ments. L'int??rieur (corps) du polygone est un autre ??l??ment, et (pour des raisons techniques) est donc le polytope nulle ou nullitope.
Un polygone g??om??trique est une r??alisation du polygone abstraite associ??e. Cela implique une certaine cartographie des ??l??ments de l'abstrait g??om??trique. Un tel polygone ne pas avoir ?? mentir dans un plan, ou ont des parois droites, ou joindre un domaine, et des ??l??ments individuels peuvent se chevaucher ou m??me co??ncider. Par exemple, un sph??rique polygone est trac?? sur la surface d'une sph??re, et ses c??t??s sont des arcs de grands cercles.
Un digone est un polygone ferm?? ayant deux c??t??s et deux angles. Deux points oppos??es sur une surface sph??rique, rejoints par deux grands demi-cercles diff??rents produisent une digone. Carrelage la sph??re avec digons produit un poly??dre appel?? hosohedron. Un grand cercle avec un point d'angle ajout??e, produit un monogon ou H??nagone.
D'autres r??alisations de ces polygones sont possibles sur d'autres surfaces, mais dans le (plat) plan euclidien, leur corps ne peuvent pas ??tre sensiblement r??alis??s et sont consid??r??es d??g??n??r??e.
L'id??e d'un polygone a ??t?? g??n??ralis?? de diverses mani??res. Une courte liste de certains cas d??g??n??r??s (ou des cas particuliers) comprend ce qui suit:
- Digon: angle int??rieur de 0 ?? dans le plan euclidien. Voir les remarques ci-dessus concernant la sph??re
- Angle int??rieur de 180 ??: Dans l'avion ce qui donne une apeirogon (voir ci-dessous), sur la sph??re une di??dre
- Un polygone d??salignement ne r??side pas dans un plan plat, mais en zigzag en trois (ou plus) dimensions. Le Polygones Petrie des poly??dres r??guliers sont des exemples classiques
- Un polygone sph??rique est un circuit de c??t??s et les coins sur la surface d'une sph??re
- Une apeirogon est une s??quence infinie de c??t??s et les angles, qui ne est pas ferm??e, mais il n'a pas d'extr??mit??s, car elle se ??tend ?? l'infini
- Un polygone complexe est une figure analogue ?? un polygone ordinaire, qui existe dans le plan complexe de Hilbert
Nommer polygones
Le mot ??polygone?? vient de Polygonum latin tardif (un nom), de grec πολύγωνον (polygōnon / polugōnon), l'utilisation du nom neutre de πολύγωνος (polygōnos / polugōnos, l'adjectif masculin), ce qui signifie ??beaucoup angle". Polygones individuels sont nomm??s (et parfois class??s) en fonction du nombre de c??t??s, la combinaison d'une grecque -derived pr??fixe num??rique avec le -gon suffixe, par exemple pentagone, dod??cagone. Le triangle , ou quadrilat??re quadrilat??re, et enn??agone ya des exceptions. Pour un grand nombre, math??maticiens ??crivent g??n??ralement le chiffre lui-m??me, par exemple, 17-gon. Une variable peut m??me ??tre utilis??, g??n??ralement n-gon. Ceci est utile si le nombre de c??t??s est utilis?? dans une formule .
Certains polygones sp??ciales ont aussi leurs propres noms; par exemple le r??gulier ??toile pentagone est ??galement connu comme le pentagramme.
| Nom | Bords | Remarques |
|---|---|---|
| H??nagone (ou monogon) | 1 | Dans le plan euclidien, d??g??n??re ?? une courbe ferm??e avec un point de sommet unique sur elle. |
| digone | 2 | Dans le plan euclidien, d??g??n??re ?? une courbe ferm??e avec deux points de sommet sur elle. |
| triangle (ou trigone) | 3 | Le polygone simple qui peut exister dans le plan euclidien. |
| quadrilat??rale (ou quadrilat??re ou t??tragone) | 4 | Le polygone simple qui peut se passer; le polygone simple qui peut ??tre concave. |
| Pentagone | 5 | Le polygone simple qui peut exister comme une ??toile r??guli??re. Une ??toile pentagone est connu comme un pentagramme ou pentacle. |
| hexagone | 6 | ??vitez "SEXAGON" = latine [sexe] + grecque. |
| heptagone | 7 | ??vitez "Septagon" = latine [Sept] + grecque. Le polygone simple telle que la forme ne est pas r??guli??re constructible avec r??gle et au compas . Cependant, il peut ??tre construit en utilisant une Neusis construction. |
| octogone | 8 | |
| enneagon ou enn??agone | 9 | "Nonagon" est couramment utilis??, mais m??le latine [novem = 9] avec le grec. Certains auteurs modernes pr??f??rent "enneagon", qui est pur grec. |
| d??cagone | 10 | |
| hend??cagone | 11 | ??vitez "undecagon" = latine [non -] + grecque. Le polygone simple telle que la forme r??guli??re ne peut ??tre construit avec la boussole, r??gle, et trisectrice angle. |
| dod??cagone | 12 | ??vitez "duodecagon" = latine [duo -] + grecque. |
| Trid??cagone (ou triskaidecagon) | 13 | |
| tetradecagon (ou tetrakaidecagon) | 14 | |
| Pentad??cagone (ou quindecagon ou pentakaidecagon) | 15 | |
| Hexadecagon (ou hexakaidecagon) | 16 | |
| Heptad??cagone (ou heptakaidecagon) | 17 | |
| Octad??cagone (ou octakaidecagon) | 18 | |
| Enn??ad??cagone (ou enneakaidecagon ou nonadecagon) | 19 | |
| Icosagone | 20 | |
| Triacontagone | 30 | |
| hectogon | 100 | "Hectogon" est le nom grec (voir hectom??tre), "centagon" est un hybride latin-grec; ni est largement attest??e. |
| chiliogone | 1000 | Ren?? Descartes, Kant , David Hume , et d'autres ont utilis?? le chiliogone comme exemple dans la discussion philosophique. |
| myriagone | 10000 | |
| megagon | 1000000 | Comme avec l'exemple de Ren?? Descartes de la chiliogone, le polygone millions verso a ??t?? utilis?? comme une illustration d'un concept bien d??fini qui ne peut pas ??tre visualis??. Le megagon est ??galement utilis?? comme une illustration de la convergence de polygones r??guliers ?? un cercle. |
| apeirogon | 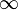 | Un polygone d??g??n??r?? d'une infinit?? de c??t??s |
Construire noms plus ??lev??s
Pour construire le nom d'un polygone avec plus de 20 et moins de 100 bords, combiner les pr??fixes comme suit
| Dizaines | et | Ones | suffixe finale | ||
|---|---|---|---|---|---|
| -Kai- | 1 | -hena- | -gon | ||
| 20 | icosa- | 2 | -di- | ||
| 30 | triaconta- | 3 | -tri- | ||
| 40 | tetraconta- | 4 | -tetra- | ||
| 50 | pentaconta- | 5 | -penta- | ||
| 60 | hexaconta- | 6 | -hexa- | ||
| 70 | heptaconta- | 7 | -hepta- | ||
| 80 | octaconta- | 8 | -octa- | ||
| 90 | enneaconta- | 9 | -ennea- | ||
Le "kai" ne est pas toujours utilis??. Les opinions divergent sur exactement quand il le devrait, ou ne doivent pas ??tre utilis??es (voir ??galement les exemples ci-dessus).
Alternativement, le syst??me utilis?? pour nommer le alcanes sup??rieurs (des hydrocarbures totalement satur??s) peuvent ??tre utilis??s:
| Ones | Dizaines | suffixe finale | ||
|---|---|---|---|---|
| 1 | Henning | 10 | d??ca | -gon |
| 2 | do- | 20 | -cosa- | |
| 3 | tri- | 30 | triaconta- | |
| 4 | t??tra | 40 | tetraconta- | |
| 5 | penta | 50 | pentaconta- | |
| 6 | hexa- | 60 | hexaconta- | |
| 7 | hepta | 70 | heptaconta- | |
| 8 | octa- | 80 | octaconta- | |
| 9 | ennea- (ou nona) | 90 | enneaconta- (ou nonaconta-) | |
Cela a l'avantage d'??tre compatible avec le syst??me utilis?? pour 10 ?? travers les chiffres 19-verso.
Ce est, une figure 42-face serait nomm?? comme suit:
| Ones | Dizaines | suffixe finale | nom complet du polygone |
|---|---|---|---|
| do- | tetraconta- | -gon | dotetracontagon |
et un chiffre de 50-face
| Dizaines | et | Ones | suffixe finale | nom complet du polygone |
|---|---|---|---|---|
| pentaconta- | -gon | pentacontagon | ||
Mais au-del?? enn??agones et d??cagones, math??maticiens professionnels pr??f??rent g??n??ralement la notation num??rique pr??cit??e (par exemple, MathWorld a articles sur 17-gones et 257-gones). Des exceptions existent pour les comptes secondaires qui sont plus facilement exprim??es sous forme verbale.
Histoire

Polygones sont connues depuis l'Antiquit??. Le polygones r??guliers ??taient connus des Grecs anciens, et de la pentagramme, un polygone r??gulier non-convexe ( polygone ??toiles), appara??t sur le vase de Aristophonus, Caere, dat?? du 7??me si??cle BC polygones non convexes en g??n??ral ne ont pas ??t?? syst??matiquement ??tudi??es jusqu'?? ce que le 14??me si??cle par Thomas Bradwardine.
En 1952, Geoffrey Colin Shephard g??n??raliser l'id??e de polygones au plan complexe, o?? chaque dimension r??elle est accompagn?? d'un imaginaire, pour cr??er polygones complexes.
Polygones dans la nature

De nombreux polygones r??guliers peuvent ??tre vus dans la nature. Dans le monde de la g??ologie , les cristaux ont des faces planes, ou facettes, qui sont des polygones. Quasicristaux peuvent m??me avoir pentagones r??guliers que visages. Un autre exemple fascinant de polygones r??guliers se produit lorsque le refroidissement de la lave forme de zones serr??es hexagonales colonnes de basalte , qui peuvent ??tre vus ?? la Chauss??e des G??ants en Irlande , ou ?? la Postpile du Diable en Californie .

Les hexagones plus c??l??bres dans la nature se trouvent dans le r??gne animal. La cire nid d'abeille faite par les abeilles est un tableau de hexagones utilis?? pour stocker le miel et le pollen, et comme un endroit s??r pour les larves de se d??velopper. Il existe ??galement des animaux qui se prennent la forme approximative de polygones r??guliers, ou au moins avoir la m??me sym??trie. Par exemple, ??toiles de mer affichent la sym??trie d'un pentagone ou, moins fr??quemment, le heptagone ou d'autres polygones. Autre ??chinodermes, comme oursins, affichent parfois sym??tries similaires. Bien ??chinodermes ne pr??sentent pas exacte sym??trie radiale, m??duses et Cn??tophores font, g??n??ralement quatre ou huit.
Sym??trie radiale (sym??trie et d'autres) est ??galement largement observ?? dans le r??gne v??g??tal, en particulier parmi les fleurs, et (dans une moindre mesure) les graines et fruits, la forme la plus commune de cette sym??trie ??tant pentagonale. Un exemple particuli??rement frappant, ce est la carambole, un fruit l??g??rement acidul?? populaire en Asie du Sud-Est, dont la section est en forme d'??toile pentagonale.
D??placement sur la terre dans l'espace, les premiers math??maticiens ?? effectuer les calculs ?? l'aide de Newton la loi de la gravitation d??couvert que si deux corps (telles que le soleil et la terre) sont en orbite autour de l'autre, il existe certains points dans l'espace, appel?? Points de Lagrange, o?? un corps plus petit (comme un ast??ro??de ou une station spatiale) restera dans une orbite stable. Le syst??me Soleil-Terre a cinq points de Lagrange. Les deux plus stables sont exactement 60 degr??s devant et derri??re la terre sur son orbite; ce est, joignant le centre du soleil et de la terre et l'un de ces points de Lagrange stables forme un triangle ??quilat??ral. Les astronomes ont d??j?? trouv?? ast??ro??des ?? ces points. Il est encore d??battue si elle est pratique pour garder une station spatiale au point de Lagrange - bien qu'il ne aurait jamais besoin des corrections de trajectoire, il aurait ?? esquiver souvent les ast??ro??des qui sont d??j?? pr??sents. Il ya d??j?? des satellites et les observatoires spatiaux aux points de Lagrange moins stables.
Polygones en infographie
Un polygone dans un syst??me infographie (g??n??ration d'image) est une forme bidimensionnelle qui est mod??lis?? et stock?? dans sa base de donn??es. Un polygone peut ??tre color??, ombrag?? et textur??, et sa position dans la base de donn??es est d??finie par les coordonn??es de ses sommets (coins).
Les conventions de nommage diff??rent de celles des math??maticiens:
- Un polygone simple ne se croise pas.
- un polygone est un polygone concave simple ayant au moins un angle int??rieur sup??rieur ?? 180 ??.
- Un polygone complexe ne se croiser.
L'utilisation de polygones dans l'imagerie en temps r??el: Le syst??me d'imagerie appelle la structure de polygones n??cessaires pour la sc??ne doit ??tre cr???? ?? partir de la base de donn??es. Ce est transf??r?? dans la m??moire active et enfin, le syst??me d'affichage (??cran, ??crans de t??l??vision, etc.) de sorte que la sc??ne peut ??tre visualis??e. Pendant ce processus, le syst??me d'imagerie rend polygones en perspective correcte pr??t pour la transmission des donn??es trait??es dans le syst??me d'affichage. Bien que les polygones sont ?? deux dimensions, gr??ce ?? l'ordinateur du syst??me, ils sont plac??s dans une sc??ne visuelle dans l'orientation correcte en trois dimensions de telle sorte que le point de vue se d??place ?? travers la sc??ne, il est per??u en 3D.
Morphing: Pour ??viter les effets artificiels aux fronti??res de polygones o?? les avions de polygones contigus sont ?? angle diff??rent, dits "Algorithmes Morphing?? sont utilis??s. Ce m??lange, adoucir ou lisser les bords du polygone afin que la sc??ne semble moins artificielle et plus comme le monde r??el.
Polygones maill??s: Le nombre de polygones maill??s ("maill??" est comme un filet de poisson) peut ??tre jusqu'?? deux fois celle de polygones unmeshed autonome, en particulier si les polygones sont contigus. Si une maille carr??e a n + 1 points (sommets) de chaque c??t??, il ya N carr?? carr??s dans le maillage, ou 2 n carr?? triangles car il ya deux triangles dans un carr??. Il n'y a (n + 1) 2/2 (n 2) par les sommets triangle. O?? n est grand, cette approche de la moiti??. Ou, chaque sommet int??rieur de la maille carr??e relie quatre bords (lignes).
nombre de polygones: Depuis un polygone peut avoir plusieurs c??t??s et ont besoin de nombreux points de la d??finir, afin de comparer un syst??me d'imagerie avec un autre, "le nombre de polygones" est g??n??ralement consid??r?? comme un triangle. En analysant les caract??ristiques d'un syst??me d'imagerie particulier, la d??finition exacte du nombre de polygones doit ??tre obtenu comme elle se applique ?? ce syst??me car il ya une certaine souplesse dans le traitement qui provoque des comparaisons deviennent non-trivial.
Vertex Count: Bien que l'utilisation de cette mesure semble ??tre proche de la r??alit??, il doit toujours ??tre pris avec un peu de sel. Depuis chaque sommet peut ??tre augment??e avec d'autres attributs (comme la couleur ou normal) la quantit?? de traitement impliqu??s ne peuvent pas ??tre d??duit trivialement. En outre, le sommet appliqu??e transformer doit ??tre pris en compte, ainsi topologie informations sp??cifiques au syst??me en cours d'??valuation mise en cache peut introduire des variations coh??rentes dans les r??sultats escompt??s post-transform??e.
Point test de polygone: En infographie et g??om??trie de calcul, il est souvent n??cessaire de d??terminer si un point donn?? P = (x 0, y 0) se trouve ?? l'int??rieur d'un polygone simple, donn?? par une s??quence de segments de ligne. Il est connu comme le Point test de polygone.




![\ Begin {align} A = \ frac12 (a_1 [a_2 \ sin (\ theta_1) + A_3 \ sin (\ + theta_1 \ theta_2) + \ cdots + a_ {n-1} \ sin (\ + theta_1 \ theta_2 + \ cdots + \ theta_ {n-2})] \\ {} + a_2 [A_3 \ sin (\ theta_2) + a_4 \ sin (\ + theta_2 \ theta_3) + \ cdots + a_ {n-1} \ sin (\ theta_2 + \ cdots + \ theta_ {n-2})] \\ {} + \ cdots + a_ {n-2} [a_ {n-1} \ sin (\ theta_ {n-2})]) \ end {align}](../../images/2168/216877.png)
