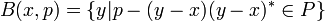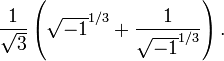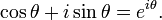Nombre complexe
?? propos de ce ??coles s??lection Wikipedia
Les articles de cette s??lection ??coles ont ??t?? organis??s par sujet du programme d'??tudes gr??ce aux b??n??voles d'enfants SOS. Tous les enfants disponibles pour le parrainage de SOS Enfants des enfants sont pris en charge dans une maison de famille pr??s de la charit??. Lire la suite ...

En math??matiques , un nombre complexe est un nombre qui peut ??tre formellement d??finie comme une paire de ordonn?? nombres r??els (a, b), souvent ??crit:
o?? i 2 = -1.
Les nombres complexes ont addition, la soustraction, la multiplication et de la division des op??rations d??finies, avec des comportements qui sont un sur-ensemble strict de nombres r??els, ainsi que d'avoir d'autres propri??t??s ??l??gantes et utiles. Notamment, les nombres r??els n??gatifs peuvent ??tre obtenus en ??levant au carr?? les nombres complexes.
Les nombres complexes ont ??t?? invent??s quand il a ??t?? d??couvert que la r??solution de certains ??quations cubiques doivent calculs interm??diaires contenant les racines carr??es des nombres n??gatifs, m??me lorsque les solutions finales ont ??t?? nombres r??els. En outre, ?? partir de la th??or??me fondamental de l'alg??bre, l'utilisation des nombres complexes comme le champ de num??ro pour polyn??mes ??quations alg??briques signifie que des solutions existent toujours. L'ensemble des nombres complexes former un alg??briquement clos champ, ?? la diff??rence de l'ensemble des nombres r??els, qui ne est pas alg??briquement clos.
Les nombres complexes sont utilis??s dans de nombreux domaines diff??rents, y compris des applications dans l'ing??nierie , l'??lectromagn??tisme , la physique quantique , les math??matiques appliqu??es , et la th??orie du chaos . Lorsque le champ sous-jacent de nombres d'un type de math??matiques est le champ de nombres complexes, le nom refl??te g??n??ralement ce fait. Des exemples sont analyse complexe, la matrice complexe , polynomiale complexe et alg??bre de Lie complexe.
D??finitions
Notation
Bien que d'autres notations peuvent ??tre utilis??s, les nombres complexes sont tr??s souvent ??crits sous la forme
o?? a et b sont des nombres r??els et i est l' unit?? imaginaire , qui a la propri??t?? i 2 = -1. Le nombre r??el a est appel?? la partie r??elle du nombre complexe, et le nombre r??el b est la partie imaginaire .
Les nombres r??els peuvent ??tre exprim??s en nombres complexes avec la partie imaginaire de z??ro; qui est, le nombre r??el a est ??quivalent au nombre complexe a 0 i. Les nombres complexes avec une partie r??elle qui est nulle sont appel??s nombres imaginaires.
Par exemple, 3 + 2 i est un nombre complexe, avec une partie r??elle et la partie imaginaire 3 2. Si z = a + ib, la partie r??elle (a) est not??e Re (z) ou 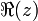 Et la partie imaginaire (b) est not??e Im (Z) ou
Et la partie imaginaire (b) est not??e Im (Z) ou 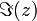 .
.
Dans certaines disciplines (en particulier, le g??nie ??lectrique , o?? i est un symbole pour actuelle), l' unit?? imaginaire i est ??crit au lieu que j, donc les nombres complexes sont parfois ??crites comme + jb.

f (x) = (x ??-1) (x -2- i) ?? /
(X ?? + 2 + 2 i). La teinte repr??sente l'argument de la fonction, tandis que la saturation repr??sente l'ampleur.
Le ensemble des nombres complexes est g??n??ralement d??sign?? par C, ou tableau noir gras par 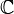 . Les nombres r??els, R, peuvent ??tre consid??r??es comme un sous-ensemble de C en consid??rant tout nombre r??el comme un complexe: A = A + 0 i.
. Les nombres r??els, R, peuvent ??tre consid??r??es comme un sous-ensemble de C en consid??rant tout nombre r??el comme un complexe: A = A + 0 i.
??galit??
Deux nombres complexes sont ??gaux si et seulement si les parties r??elles sont ??gales et leurs parties imaginaires sont ??gales. Ce est, a + c = bi + di si et seulement si a = c et b = d.
Op??rations
Les nombres complexes sont additionn??es, soustraites, multipli??es, et divis??s en appliquant formellement le associative , commutative et lois de l'alg??bre de distribution, ainsi que l'??quation i 2 = -1:
- Addition:

- Soustraction:
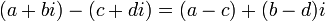
- Multiplication:

- Division:
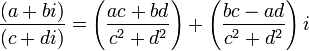
- Addition:
(Division des nombres complexes est encore d??fini ult??rieurement).
Le champ de nombres complexes
Formellement, les nombres complexes peuvent ??tre d??finis en tant que couples de nombres r??els (a, b) ainsi que les op??rations:
Ainsi d??fini, les nombres complexes forment un champ, le champ de nombre complexe, not??e C (un champ est une structure alg??brique dans laquelle addition, soustraction, multiplication et division sont d??finies et r??pondent ?? certaines lois alg??briques. Par exemple, les nombres r??els forment un champ).
Le nombre r??el est identifi?? par un nombre complexe (a, 0), et de cette fa??on le champ de nombres r??els R devient un sous-corps de C. L' unit?? imaginaire i peut alors ??tre d??finie comme le nombre complexe (0, 1), qui v??rifie
En C, nous avons:
- identit?? additif (??z??ro??): (0, 0)
- identit?? multiplicative ("un"): (1, 0)
- inverse additif de (a, b): (- a, - b)
- inverse multiplicatif (r??ciproque) de non-z??ro (a, b):

Depuis un certain nombre complexe a + bi est sp??cifi??e de mani??re unique par un couple (A, B) de nombres r??els, des nombres complexes sont en une-??-une correspondance avec des points sur un plan, appel?? le plan complexe .
C peut ??galement ??tre d??finie comme ??tant la fermeture topologique du nombres alg??briques ou que le cl??ture alg??brique de R, qui sont tous deux d??crits ci-dessous.
Le plan complexe

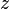 et son conjugu??
et son conjugu?? 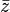 dans le plan complexe.
dans le plan complexe. Un nombre complexe z peut ??tre consid??r??e comme un point ou un vecteur de position dans un ?? deux dimensions du syst??me de coordonn??es cart??siennes appel?? le plan complexe ou Argand diagramme (nomm?? d'apr??s Jean-Robert Argand) - voir figure ?? droite. Le point et donc le nombre complexe z peuvent ??tre sp??cifi??s par cart??sienne (rectangulaire) coordonn??es. Les coordonn??es cart??siennes du nombre complexe sont la partie r??elle x = Re (z) et la partie imaginaire y = Im (z). La repr??sentation d'un nombre complexe par ses coordonn??es cart??siennes est appel??e la forme cart??sienne ou la forme rectangulaire ou forme alg??brique de ce nombre complexe.
Valeur absolue, la conjugaison et la distance
La valeur absolue (ou module) ou amplitude d'un nombre complexe  est d??fini comme ??tant
est d??fini comme ??tant 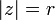 . Alg??briquement, si
. Alg??briquement, si  , Puis
, Puis 
On peut v??rifier facilement que la valeur absolue a trois propri??t??s importantes:
 si et seulement si
si et seulement si 
 ( in??galit?? triangulaire)
( in??galit?? triangulaire)
pour tous les nombres complexes z et w. Il se ensuit donc, par exemple, que 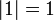 et
et  . En d??finissant la fonction de distance
. En d??finissant la fonction de distance 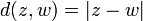 nous nous tournons l'ensemble des nombres complexes dans un espace m??trique et nous pouvons donc parler de limites et la continuit??.
nous nous tournons l'ensemble des nombres complexes dans un espace m??trique et nous pouvons donc parler de limites et la continuit??.
Le complexe conjugu?? du nombre complexe  est d??fini comme ??tant
est d??fini comme ??tant  , ??crit
, ??crit 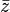 ou
ou  . Comme on le voit sur la figure,
. Comme on le voit sur la figure, 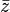 est le ??reflet?? de z sur l'axe r??el. Ce qui suit peut ??tre v??rifi??:
est le ??reflet?? de z sur l'axe r??el. Ce qui suit peut ??tre v??rifi??:
 si et seulement si z est r??el
si et seulement si z est r??el
 si et seulement si z est purement imaginaire
si et seulement si z est purement imaginaire
 si z est diff??rent de z??ro.
si z est diff??rent de z??ro.
Cette derni??re formule est la m??thode de choix pour calculer l'inverse d'un nombre complexe si elle est donn??e en coordonn??es rectangulaires.
Qui commute de conjugaison avec toutes les op??rations alg??briques (et de nombreuses fonctions; par exemple,  ) Est enracin??e dans l'ambigu??t?? dans le choix de i (-1 a deux racines carr??es). Il est important de noter, cependant, que la fonction
) Est enracin??e dans l'ambigu??t?? dans le choix de i (-1 a deux racines carr??es). Il est important de noter, cependant, que la fonction  ne est pas complexe diff??rentiable (voir fonction holomorphe).
ne est pas complexe diff??rentiable (voir fonction holomorphe).
Fractions complexes
Nous pouvons diviser un nombre complexe (a + bi) par un autre nombre complexe (c + di) ≠ 0 de deux fa??ons. La premi??re a d??j?? ??t?? implicite: pour convertir les deux nombres complexes sous forme exponentielle, ?? partir de laquelle leur quotient est facilement d??duite. La deuxi??me fa??on consiste ?? exprimer la division comme une fraction, puis de multiplier le num??rateur et le d??nominateur par le conjugu?? complexe du d??nominateur. Le nouveau d??nominateur est un nombre r??el.
Interpr??tation g??om??trique des op??rations sur les nombres complexes



Consid??rons un avion . Un point est ?? l'origine, 0. Un autre point est l'unit??, ou 1.
La somme des deux points A et B est le point X = A + B de telle sorte que les triangles dont les sommets 0, A, B et X, B, A, sont congruents.
Le produit de deux points A et B est le point X = AB de telle sorte que les sommets des triangles avec 0, 1, A et 0, B, X, sont similaire.
Le conjugu?? complexe d'un point A est le point X = A * tel que les sommets des triangles avec 0, 1, A, et 0, 1, X, sont des images sp??culaires l'une de l'autre.
Cette interpr??tation g??om??trique permet probl??mes de g??om??trie ?? ??tre traduits en alg??bre. Le probl??me de la construction g??om??trique de la 17-gon se traduit donc dans l'analyse de l'??quation alg??brique x 17 = 1.
Forme polaire
En variante ?? la repr??sentation cart??sienne z = x + iy, le nombre complexe z peut ??tre sp??cifi??e en coordonn??es polaires . Les coordonn??es polaires sont r = | z | ≥ 0, dite valeur absolue ou module et φ = arg (z), appel?? l'argument ou l'angle de z. Pour r = 0 ne importe quelle valeur de φ d??crit le m??me num??ro. Pour obtenir une repr??sentation unique, un choix classique est de mettre en arg (0) = 0. Pour r> 0 l'argument φ est unique modulo 2π; qui est, si deux valeurs de l'argument complexe diff??rent par une exacte nombre entier multiple de 2π, ils sont consid??r??s comme ??quivalents. Pour obtenir une repr??sentation unique, un choix classique consiste ?? φ limiter ?? l'intervalle (-π, π], ce est ?? dire -π <φ ≤ π. La repr??sentation d'un nombre complexe par ses coordonn??es polaires est appel??e la forme polaire du nombre complexe .
Conversion de la forme polaire ?? la forme cart??sienne
Conversion de la forme cart??sienne ?? la forme polaire
(Voir arg et fonction atan2.)
La valeur obtenue pour φ est dans la gamme (-π, + π];. Il est n??gatif pour les valeurs n??gatives de y Si les valeurs ?? la place non-n??gatives dans l'intervalle [0, 2π) sont souhait??es, ajouter 2π ?? des r??sultats n??gatifs.
Notation de la forme polaire
La notation de la forme polaire
est appel?? forme trigonom??trique. Le φ notation cis est parfois utilis?? comme une abr??viation pour cos φ + i sin φ. Utilisation La formule d'Euler il peut aussi se ??crire
qui est appel?? forme exponentielle.
Multiplication, division, exponentiation, et l'extraction de la racine dans la forme polaire
Multiplication, division, exponentiation, et l'extraction des racines sont beaucoup plus faciles dans la forme polaire que dans la forme cart??sienne.
Utilisation somme et la diff??rence des identit??s son possible pour obtenir que
et cela
Exponentiation avec exposants entiers; selon La formule de De Moivre,
Exponentiation avec des exposants complexes arbitraires est discut??e dans l'article sur exponentiation .
L'addition de deux nombres complexes ne est que la somme vectorielle de deux vecteurs, et la multiplication par un nombre complexe fixe peut ??tre consid??r?? comme une rotation et d'??tirage simultan??.
La multiplication par i correspond ?? une rotation dans le sens antihoraire de 90 degr??s (π / 2 radians ). Le contenu g??om??trique de l'??quation i 2 = -1 est qu'une s??quence de deux rotations de 90 degr??s r??sultats ?? un degr?? 180 (π radians) de rotation. M??me le fait (-1) ?? (-1) = 1 de l'arithm??tique peut ??tre compris g??om??triquement comme la combinaison de deux virages ?? 180 degr??s.
Toutes les racines de ne importe quel nombre, r??el ou complexe, peuvent ??tre trouv??s avec un simple algorithme . La n-i??me racines sont donn??s par
pour k = 0, 1, 2, ..., n - 1, o?? ![\ Sqrt [n] {r}](../../images/145/14548.png) repr??sente le principal n i??me racine de r.
repr??sente le principal n i??me racine de r.
Certaines propri??t??s
Repr??sentation matricielle des nombres complexes
Bien que g??n??ralement pas utile, des repr??sentations alternatives du domaine complexe peuvent donner une id??e de sa nature. Une repr??sentation particuli??rement ??l??gante interpr??te chaque nombre complexe comme une 2 ?? 2 matrice avec de vraies entr??es qui se ??tend et tourne les points du plan. Chaque telle matrice a la forme
o?? a et b sont des nombres r??els. La somme et le produit de deux de ces matrices est ?? nouveau de cette forme, et l'op??ration de produit sur des matrices de cette forme est commutative . Chaque matrice non-z??ro de ce formulaire est inversible et son inverse est nouveau de ce formulaire. Par cons??quent, les matrices de cette forme sont un terrain, isomorphe au champ de nombres complexes. Chaque telle matrice peut se ??crire
ce qui sugg??re que nous devrions identifier le v??ritable num??ro 1 avec la matrice d'identit??
et i l'unit?? imaginaire avec
une rotation dans le sens antihoraire de 90 degr??s. Notez que le carr?? de cette derni??re matrice est en effet ??gale ?? la matrice 2 ?? 2 qui repr??sente -1.
Le carr?? de la valeur absolue d'un nombre complexe exprim?? sous forme de matrice est ??gal au d??terminant de cette matrice.
Si la matrice est consid??r??e comme une transformation de l'avion, puis la transformation des points tourne d'un angle ??gal ?? l'argument du nombre complexe et ??chelles par un facteur ??gal ?? la valeur absolue du nombre complexe. Le conjugu?? du nombre complexe z correspond ?? la transformation qui fait tourner par l'interm??diaire du m??me angle que z mais dans la direction oppos??e, et les ??chelles de la m??me mani??re que z; cela peut ??tre repr??sent?? par la transpos??e de la matrice correspondant ?? z.
Si les ??l??ments de matrice sont eux-m??mes nombres complexes, l'alg??bre obtenue est celle de la quaternions. En d'autres termes, cette repr??sentation matricielle est une fa??on d'exprimer la La construction de Cayley-Dickson d'alg??bres.
Il convient ??galement de noter que les deux valeurs propres de la matrice de 2x2 repr??sentant un nombre complexe sont le nombre complexe lui-m??me et de son conjugu??.
Espace vectoriel r??el
C est un vrai deux dimensions espace vectoriel . Contrairement aux r??els, l'ensemble des nombres complexes ne peut pas ??tre totalement ordonn?? d'une fa??on qui est compatible avec ses op??rations arithm??tiques: C ne peut pas ??tre transform?? en un corps ordonn??. Plus g??n??ralement, aucun champ contenant une racine carr??e de -1 peut ??tre command??.
Cartes -lin??aire R C → C ont la forme g??n??rale
?? coefficients complexes a et b. Seul le premier terme est C-lin??aires, et seul le premier terme est holomorphe; le second terme est r??el diff??rentiables, mais ne satisfait pas le ??quations de Cauchy-Riemann.
La fonction
correspond ?? des rotations combin??es avec mise ?? l'??chelle, tandis que la fonction
correspond ?? des r??flexions combin??es avec mise ?? l'??chelle.
Les solutions d'??quations polynomiales
A la racine du polyn??me p est un nombre complexe z de telle sorte que p (z) = 0. Un r??sultat surprenant dans l'analyse complexe est que tous les polyn??mes de degr?? n ?? coefficients r??els ou complexes ont des racines complexes exactement n (comptage racines multiples en fonction de leur multiplicit??). Ceci est connu comme la th??or??me fondamental de l'alg??bre, et il montre que les nombres complexes sont un corps alg??briquement clos.
En effet, le champ de nombre complexe C est la cl??ture alg??brique du champ de nombre r??el, et Cauchy construit le domaine des nombres complexes de cette mani??re. Il peut ??galement ??tre caract??ris?? comme le anneau quotient du polyn??me anneau R [X] sur le id??al engendr?? par le polyn??me X ?? + 1:
Ce est en effet un champ parce que X ?? + 1 est irr??ductible, d'o?? la g??n??ration d'un id??al maximal, dans la R [X]. L'image de X dans cet anneau de quotient est l'unit?? imaginaire i.
Alg??brique caract??risation
Le champ C est ( jusqu'?? terrain isomorphisme) caract??ris?? par les trois faits suivants:
- son caract??ristique est 0
- son degr?? de transcendance sur la corps premier est le cardinalit?? du continuum
- il est alg??briquement clos
Par cons??quent, C contient de nombreux sous-champs qui sont propres isomorphe ?? C. Une autre cons??quence de cette caract??risation est que le Groupe de Galois de C sur les nombres rationnels est ??norme, de cardinal ??gal ?? celle de l'ensemble du continuum de puissance.
Caract??risation comme un champ topologique
Comme indiqu?? plus haut, la caract??risation alg??brique de C ne rend pas compte de certaines de ses propri??t??s les plus importantes. Ces propri??t??s, qui sous-tendent les fondements de analyse complexe, r??sultent de la topologie de C. Les propri??t??s suivantes caract??risent en C champ topologique:
- C est un champ.
- C contient un sous-ensemble d'??l??ments non nuls P satisfaisants:
- P est ferm?? pour l'addition, la multiplication et prenant inverses.
- Si x et y sont des ??l??ments distincts de P, alors soit xy ou yx est ?? P
- Si S est tout sous-ensemble non vide de P, alors S + P = x + P pour certains x dans C.
- C a un automorphisme involutif non trivial x → x *, fixant P et tel que xx * est en P pour tout x non nuls dans C.
Compte tenu de ces propri??t??s, on peut alors d??finir une topologie sur C en prenant les s??ries
comme un base, o?? x parcourt C, et p gammes sur P.
Pour voir que ces propri??t??s caract??risent C comme champ topologique, on constate que P ∪ {0} ∪ -P est un ordonn?? Champ Dedekind-compl??te, et donc peuvent ??tre identifi??s avec le nombres r??els R par un isomorphisme de champ unique. La derni??re propri??t?? est facilement visible impliquer que le Groupe de Galois sur les nombres r??els est d'ordre deux, compl??tant la caract??risation.
Pontriaguine a montr?? que la seule li?? localement compact champs topologiques sont R et C. Cela donne une autre caract??risation de C comme un champ topologique, puisque C peut ??tre distingu??e de R en notant que les nombres complexes non nuls connect??, tandis que les nombres r??els non nuls ne sont pas.
Analyse complexe
L'??tude des fonctions d'une variable complexe est connu comme analyse complexe et a un ??norme utilisation pratique dans les math??matiques appliqu??es ainsi que dans d'autres branches des math??matiques. Souvent, les preuves les plus naturels pour les d??clarations en analyse r??elle ou m??me la th??orie des nombres emploient des techniques de l'analyse complexe (voir th??or??me des nombres premiers pour un exemple). Contrairement fonctions r??elles qui sont couramment repr??sent??s comme deux dimensions graphiques, fonctions complexes ont quatre dimensions graphiques et peuvent utilement ??tre illustr??s par un codage couleur trois dimensions graphique de proposer quatre dimensions, ou en animant transformation dynamique de la fonction complexe du plan complexe.
Applications
Les mots "r??els" et "imaginaires" ??taient sens quand les nombres complexes ont ??t?? utilis??s principalement comme une aide dans la manipulation de chiffres ??r??els??, avec seulement la partie ??r??el?? d??crivant directement le monde. Des applications plus tardives, et en particulier la d??couverte de la m??canique quantique, a montr?? que la nature n'a pas de pr??f??rence pour les nombres ??r??els?? et ses plus r??el descriptions exigent souvent des nombres complexes, la partie ??imaginaire?? ??tant tout aussi physique que la partie ??r??el??.
La th??orie du contr??le
Dans la th??orie du contr??le , les syst??mes sont souvent transform??s de la dans le domaine temporel ?? la domaine de fr??quence en utilisant la Transform??e de Laplace. Le syst??me de p??les et les z??ros sont ensuite analys??s dans le plan complexe. Le lieu des racines, Diagramme de Nyquist, et Techniques de l'intrigue Nichols font toute utilisation du plan complexe.
Dans le proc??d?? de lieu des p??les, il est particuli??rement important si le p??les et z??ros sont dans les plans de moiti?? gauche ou ?? droite, ce est ?? dire avoir une v??ritable partie sup??rieure ou inf??rieure ?? z??ro. Si un syst??me a des p??les qui sont
- dans le demi-plan droit, il sera instable,
- tous dans le demi-plan gauche, il sera stable,
- sur l'axe imaginaire, elle aura stabilit?? marginale.
Si un syst??me a des z??ros dans le demi-plan droit, ce est un syst??me de phase nonminimum.
Analyse des signaux
Les nombres complexes sont utilis??s dans l'analyse du signal et d'autres domaines pour une description commode pour les signaux variant p??riodiquement. Pour les fonctions indiqu??es repr??sentant quantit??s physiques r??elles, souvent en termes de sinus et cosinus, les fonctions complexes correspondant sont consid??r??s dont les parties r??elles sont les quantit??s originales. Pour un onde sinuso??dale d'une donn??e la fr??quence, la valeur absolue | z | z de la correspondante est la amplitude et l'argument arg (z) le phase.
Si L'analyse de Fourier est utilis??e pour ??crire un signal de valeur r??elle donn??e comme une somme de fonctions p??riodiques, ces fonctions p??riodiques sont souvent ??crites comme des fonctions de valeurs complexes de la forme
o?? ω repr??sente la la fr??quence angulaire et du nombre complexe z code pour la phase et l'amplitude, comme expliqu?? ci-dessus.
En g??nie ??lectrique , le Transform??e de Fourier est utilis??e pour analyser divers tensions et courants. Le traitement de des r??sistances, condensateurs, et inductances peuvent ??tre unifi??s par l'introduction, les r??sistances d??pendant de la fr??quence imaginaires de ces deux derniers et ?? combiner tous les trois dans un seul nombre complexe appel?? le imp??dance. (Ing??nieurs ??lectriques et certains physiciens utilisent la lettre j pour l'unit?? imaginaire depuis i est g??n??ralement r??serv??e aux courants divers et peuvent entrer en conflit avec i.) Cette approche est appel??e calcul phaseur. Cette utilisation est aussi ??tendue ?? traitement num??rique du signal et traitement d'image num??rique, qui utilisent des versions num??riques de l'analyse de Fourier (et Analyse en ondelettes) pour transmettre, comprimer, restaurer et contraire processus num??riques audio signaux, d'images fixes, et signaux vid??o.
Int??grales impropres
Dans les domaines appliqu??s, les nombres complexes sont souvent utilis??s pour calculer certaines valeurs r??elles int??grales impropres, au moyen de fonctions ?? valeurs complexes. Plusieurs m??thodes existent pour ce faire; voir m??thodes d'int??gration de contour.
M??canique quantique
Le champ de nombre complexe est pertinente dans le formulation math??matique de la m??canique quantique, o?? complexe Espaces de Hilbert fournissent le contexte pour une telle formulation qui est pratique et peut-??tre plus standard. Les formules de base d'origine de la m??canique quantique - la Schr??dinger ??quation et Heisenberg m??canique matricielle - font usage des nombres complexes.
Relativit??
Dans sp??ciale et la relativit?? g??n??rale , certaines formules pour la m??trique sur espace-temps deviennent plus simples si l'on prend la variable de temps pour ??tre imaginaire. (Ce ne est plus la norme.) Les nombres complexes sont essentiels pour spineurs qui sont une g??n??ralisation de la tenseurs utilis??s dans la relativit??.
Math??matiques appliqu??es
Dans les ??quations diff??rentielles , il est fr??quent de trouver d'abord toutes les racines complexes de la r ??quation caract??ristique d'un ??quation diff??rentielle lin??aire et ensuite tenter de r??soudre le syst??me en termes de fonctions de base de la forme f (t) = e rt.
La dynamique des fluides
En la dynamique des fluides, des fonctions complexes sont utilis??s pour d??crire ??coulement potentiel en deux dimensions.
Fractales
Certains fractales sont trac??es dans le plan complexe par exemple ensemble de Mandelbrot et Ensemble de Julia.
Histoire
La premi??re r??f??rence fugace racines carr??es de nombres n??gatifs peut-??tre eu lieu dans le travail de la grecque math??maticien et inventeur H??ron d'Alexandrie dans le 1er si??cle apr??s JC , quand il a examin?? le volume d'un impossible tronc de pyramide , si les nombres n??gatifs ne ont pas ??t?? con??us dans le Monde hell??nistique.
Les nombres complexes sont devenus plus importants dans le 16??me si??cle , quand il est ferm?? formules pour les racines de cubique et quartiques polyn??mes ont ??t?? d??couverts par les math??maticiens italiens (voir Niccolo Fontana Tartaglia, J??r??me Cardan). Il est vite rendu compte que ces formules, m??me si l'on ??tait seulement int??ress?? par des solutions r??elles, parfois n??cessaires la manipulation des racines carr??es des nombres n??gatifs. Par exemple, la formule cube de Tartaglia donne la solution suivante ?? l'??quation x ?? - x = 0:
?? premi??re vue, cela ressemble ?? un non-sens. Cependant calculs formels avec des nombres complexes montrent que l'??quation z = i 3 a des solutions -i,  et
et  . En substituant ?? leur tour pour
. En substituant ?? leur tour pour  dans la formule cube de Tartaglia et en simplifiant, on obtient 0, 1 et -1 comme les solutions de x 3 - x = 0.
dans la formule cube de Tartaglia et en simplifiant, on obtient 0, 1 et -1 comme les solutions de x 3 - x = 0.
Ce ??tait doublement troublante puisque m??me pas les nombres n??gatifs ont ??t?? consid??r??s comme sur la terre ferme ?? l'??poque. Le terme ??imaginaire?? pour ces quantit??s a ??t?? invent?? par Ren?? Descartes 1637 et qui devait ??tre d??rogatoire (voir nombre imaginaire pour une discussion sur la ??r??alit???? des nombres complexes). Une autre source de confusion est que l'??quation 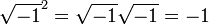 semblait ??tre capricieusement incompatible avec l'identit?? alg??brique
semblait ??tre capricieusement incompatible avec l'identit?? alg??brique  , Qui est valable pour r??el positif nombres a et b, et qui a ??galement ??t?? utilis?? dans les calculs de nombres complexes avec l'un des a, b positif et l'autre n??gatif. L'utilisation incorrecte de cette identit?? (et l'identit?? li??es
, Qui est valable pour r??el positif nombres a et b, et qui a ??galement ??t?? utilis?? dans les calculs de nombres complexes avec l'un des a, b positif et l'autre n??gatif. L'utilisation incorrecte de cette identit?? (et l'identit?? li??es  ) Dans le cas o?? a et b sont n??gatifs, m??me tourment?? Euler . Cette difficult?? a finalement conduit ?? la convention d'utiliser le symbole sp??cial i ?? la place de
) Dans le cas o?? a et b sont n??gatifs, m??me tourment?? Euler . Cette difficult?? a finalement conduit ?? la convention d'utiliser le symbole sp??cial i ?? la place de  pour se pr??munir contre cette erreur.
pour se pr??munir contre cette erreur.
Le 18??me si??cle a vu les travaux de Abraham de Moivre et Leonhard Euler . Pour de Moivre est due (1730) la formule bien connue qui porte son nom, la formule de de Moivre:
et ?? Euler (1748) La formule d'Euler de analyse complexe:
L'existence de nombres complexes ne ??tait pas compl??tement accept?? jusqu'?? l'interpr??tation g??om??trique (voir ci-dessous) a ??t?? d??crit par Caspar Wessel en 1799 ; il a ??t?? red??couvert quelques ann??es plus tard et popularis?? par Carl Friedrich Gauss , et par cons??quent la th??orie des nombres complexes a re??u une expansion notable. L'id??e de la repr??sentation graphique des nombres complexes ??tait apparu, cependant, d??s 1685, dans Le Tractatus de l'alg??bre de Wallis.
Les m??moires de Wessel est apparu dans les Actes de la Copenhague Acad??mie pour 1799, et est extr??mement claire et compl??te, m??me en comparaison avec des ??uvres modernes. Il consid??re aussi que la sph??re, et donne une la th??orie de quaternion ?? partir de laquelle il d??veloppe une trigonom??trie sph??rique compl??te. En 1804, l'abb?? Bu??e est venu de fa??on autonome la m??me id??e qui Wallis avait sugg??r??, que 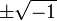 devrait repr??senter une ligne de l'unit??, et son n??gatif, perpendiculaire ?? l'axe r??el. Le document de bu??e ne fut publi??e qu'en 1806, ann??e o?? Jean-Robert Argand a ??galement publi?? une brochure sur le m??me sujet. Il est ?? l'essai de Argand que la fondation scientifique pour la repr??sentation graphique des nombres complexes est maintenant g??n??ralement appel??. N??anmoins, en 1831 Gauss trouv?? la th??orie tout ?? fait inconnu, et en 1832 a publi?? ses m??moires en chef sur le sujet, l'amenant ainsi en ??vidence devant le monde math??matique. Mention devrait ??galement ??tre faite d'un excellent petit trait?? par Mourey (1828), dans lequel les bases de la th??orie des nombres directionnelles sont scientifiquement ??tabli. L'acceptation g??n??rale de la th??orie ne est pas un peu en raison de travaux de Augustin Louis Cauchy et Niels Henrik Abel, et surtout ce dernier, qui ??tait le premier ?? utiliser hardiment nombres complexes avec un succ??s qui est bien connu.
devrait repr??senter une ligne de l'unit??, et son n??gatif, perpendiculaire ?? l'axe r??el. Le document de bu??e ne fut publi??e qu'en 1806, ann??e o?? Jean-Robert Argand a ??galement publi?? une brochure sur le m??me sujet. Il est ?? l'essai de Argand que la fondation scientifique pour la repr??sentation graphique des nombres complexes est maintenant g??n??ralement appel??. N??anmoins, en 1831 Gauss trouv?? la th??orie tout ?? fait inconnu, et en 1832 a publi?? ses m??moires en chef sur le sujet, l'amenant ainsi en ??vidence devant le monde math??matique. Mention devrait ??galement ??tre faite d'un excellent petit trait?? par Mourey (1828), dans lequel les bases de la th??orie des nombres directionnelles sont scientifiquement ??tabli. L'acceptation g??n??rale de la th??orie ne est pas un peu en raison de travaux de Augustin Louis Cauchy et Niels Henrik Abel, et surtout ce dernier, qui ??tait le premier ?? utiliser hardiment nombres complexes avec un succ??s qui est bien connu.
Les termes courants utilis??s dans la th??orie sont principalement due aux fondateurs. Argand appel??  le facteur de direction, et
le facteur de direction, et  le module; Cauchy (1828) appel??
le module; Cauchy (1828) appel??  la forme r??duite (l'expression R??duite); Gauss i utilis?? pour
la forme r??duite (l'expression R??duite); Gauss i utilis?? pour  , A pr??sent?? le num??ro de complexe terme pour
, A pr??sent?? le num??ro de complexe terme pour  , Et a appel??
, Et a appel?? 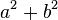 la norme.
la norme.
Le coefficient de direction d'expression, souvent utilis?? pour  , Est due ?? Hankel (1867), et la valeur absolue, par module, est due ?? Weierstrass.
, Est due ?? Hankel (1867), et la valeur absolue, par module, est due ?? Weierstrass.
Apr??s Cauchy et Gauss ont parcouru un nombre de contributeurs de haut rang, dont celui-ci peut ??tre en particulier mentionn??: Kummer (1844), Leopold Kronecker (1845), Scheffler (1845, 1851, 1880), Bellavitis (1835, 1852), Peacock (1845), et De Morgan (1849). M??bius doit ??galement ??tre mentionn?? pour ses nombreux m??moires sur les applications g??om??triques de nombres complexes, et Dirichlet pour l'expansion de la th??orie des nombres premiers d'inclure, congruences, r??ciprocit??, etc., comme dans le cas de nombres r??els.
Un complexe anneau ou domaine est un ensemble de nombres complexes qui est ferm?? sous l'addition, la soustraction et la multiplication. Gauss ??tudi?? nombres complexes de la forme  , O?? a et b sont solidaires, ou rationnelle (et i est l'un des deux racines de
, O?? a et b sont solidaires, ou rationnelle (et i est l'un des deux racines de  ). Son ??l??ve, Ferdinand Eisenstein, a ??tudi?? le type
). Son ??l??ve, Ferdinand Eisenstein, a ??tudi?? le type  O??
O??  est une racine complexe de
est une racine complexe de  . Telles autres cat??gories (appel??s corps cyclotomiques) de nombres complexes sont d??riv??es de la racines de l'unit??
. Telles autres cat??gories (appel??s corps cyclotomiques) de nombres complexes sont d??riv??es de la racines de l'unit?? 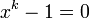 pour des valeurs sup??rieures de
pour des valeurs sup??rieures de 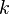 . Cette g??n??ralisation est largement d?? ?? Kummer, qui a aussi invent?? num??ros id??ales, qui ont ??t?? exprim??s comme des entit??s g??om??triques par Felix Klein en 1893. La th??orie g??n??rale des champs a ??t?? cr???? par ??variste Galois, qui a ??tudi?? les champs g??n??r??s par les racines de toute ??quation polynomiale
. Cette g??n??ralisation est largement d?? ?? Kummer, qui a aussi invent?? num??ros id??ales, qui ont ??t?? exprim??s comme des entit??s g??om??triques par Felix Klein en 1893. La th??orie g??n??rale des champs a ??t?? cr???? par ??variste Galois, qui a ??tudi?? les champs g??n??r??s par les racines de toute ??quation polynomiale
Les ??crivains fin (de 1884) sur la th??orie g??n??rale comprennent Weierstrass, Schwarz, Richard Dedekind, Otto H??lder, Bonaventure Berloty, Henri Poincar??, Eduard Study, et Alexander MacFarlane.
La d??finition formellement correcte en utilisant des paires de nombres r??els a ??t?? donn?? dans le 19??me si??cle .




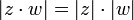
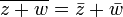
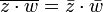




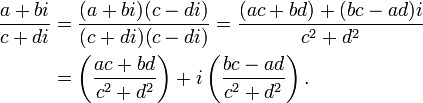
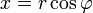



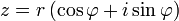
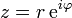



![\ Sqrt [n] {re ^ {i \ varphi}} = \ sqrt [n] {r} \ e ^ {i \ left (\ frac {\ varphi + 2k \ pi} {n} \ right)}](../../images/145/14547.png)








![\ Mathbb {C} = \ mathbb {R} [X] / (X ^ 2 + 1). \,](../../images/145/14557.png)