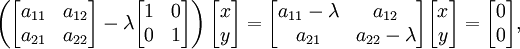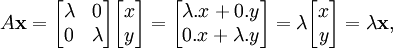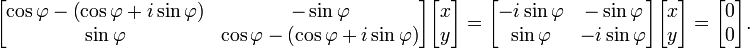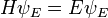Valeurs et vecteurs propres
Renseignements g??n??raux
SOS Enfants a fait cette s??lection Wikipedia aux c??t??s d'autres ??coles des ressources . Voir http://www.soschildren.org/sponsor-a-child pour conna??tre le parrainage d'enfants.

En math??matiques , un vecteur peut ??tre consid??r?? comme une fl??che. Il a une longueur, appel?? son ampleur, et il souligne dans une direction particuli??re. Un transformation lin??aire peut ??tre consid??r?? pour fonctionner sur un vecteur pour le changer, en changeant souvent fois par son ampleur et sa direction. Un vecteur propre d'une transformation lin??aire donn??e est un vecteur qui est multipli?? par une constante appel??e valeurs propres au cours de cette transformation. La direction du vecteur propre est soit inchang??e par cette transformation (par valeurs propres positives) ou invers??e (pour valeurs propres n??gatives).
Par exemple, une valeur propre de 2 signifie que le vecteur propre est doubl?? en longueur et points dans la m??me direction. Une valeur propre de 1 signifie que le vecteur propre est inchang??e, tandis qu'une valeur propre de -1 signifie que le vecteur propre est invers??e dans la direction. Un espace propre d'une transformation donn??e est la dur??e des vecteurs propres de cette transformation avec la m??me valeur propre, ainsi que le vecteur nul (ce qui n'a pas de direction). Un espace propre est un exemple d'un sous-espace d'un espace vectoriel .
En alg??bre lin??aire , chaque transformation lin??aire entre les espaces vectoriels de dimension finie peut ??tre donn??e par une matrice , qui est un tableau rectangulaire de nombres dispos??s en rang??es et en colonnes. Les m??thodes standard pour trouver les valeurs propres, vecteurs propres et espaces propres d'une matrice donn??e sont discut??s ci-dessous.
Ces concepts jouent un r??le majeur dans plusieurs branches de fois pures et math??matiques appliqu??es - apparaissant en bonne place dans l'alg??bre lin??aire , analyse fonctionnelle, et dans une moindre mesure en math??matiques non lin??aires.
De nombreux types d'objets math??matiques peuvent ??tre trait??s comme des vecteurs: fonctions , modes harmoniques, ??tats quantiques, et fr??quences, par exemple. Dans ces cas, le concept de direction perd son sens ordinaire, et est donn?? une d??finition abstraite. Toutefois, si cette direction est inchang?? abstraite par une transformation lin??aire donn??, le pr??fixe ??eigen" est utilis??, comme dans fonction propre, mode propre, ??tat propre et fr??quence propre.
Histoire
Les valeurs propres sont souvent introduits dans le cadre de l'alg??bre lin??aire ou th??orie de la matrice . Historiquement, cependant, ils ont ??t?? soulev??es dans l'??tude de formes et quadratique ??quations diff??rentielles .
Euler avait ??galement ??tudi?? le mouvement d'une rotation corps rigide et d??couvert l'importance de la axes principaux. Comme Lagrange r??alis??, les axes principaux sont les vecteurs propres de la matrice d'inertie. Au d??but du 19e si??cle, Cauchy a vu comment leur travail pourrait ??tre utilis?? pour classer le quadriques, et il g??n??ralis??s aux dimensions arbitraires. Cauchy a aussi invent?? la Caract??ristique de racine terme (racine caract??ristique) pour ce qui est maintenant appel?? valeur propre; son mandat survit dans ??quation caract??ristique.
Fourier utilis?? le travail de Laplace et Lagrange pour r??soudre le ??quation de la chaleur par s??paration des variables dans son c??l??bre livre 1822 Th??orie analytique de la chaleur. Sturm a d??velopp?? les id??es de Fourier plus loin et il les conduisit ?? l'attention de Cauchy, qui les combine avec ses propres id??es et il est arriv?? par le fait que les matrices sym??triques ont de vraies valeurs propres. Cela a ??t?? prolong??e par Hermite en 1855 ?? ce que l'on appelle aujourd'hui Matrices hermitiennes. Vers la m??me ??poque, Brioschi prouv?? que les valeurs propres de matrices orthogonales se trouvent sur le cercle unit??, et Clebsch trouv?? le r??sultat correspondant pour antisym??triques matrices. Finalement, Weierstrass clarifi?? un aspect important dans la th??orie de la stabilit?? commenc?? par Laplace en r??alisant que matrices d??fectueux peuvent provoquer une instabilit??.
Pendant ce temps, Liouville a ??tudi?? les probl??mes de valeurs propres similaires ?? celles de Sturm; la discipline qui est n??e de leur travail est maintenant appel?? Th??orie de Sturm-Liouville. Schwarz a ??tudi?? la premi??re valeur propre de L'??quation de Laplace sur les domaines g??n??raux vers la fin du 19??me si??cle, tandis que Poincar?? a ??tudi?? L'??quation de Poisson quelques ann??es plus tard.
Au d??but du 20e si??cle, Hilbert a ??tudi?? les valeurs propres de op??rateurs int??graux en consultant les op??rateurs comme matrices infinies. Il ??tait le premier ?? utiliser le allemand eigen mot pour d??signer valeurs et vecteurs propres en 1904, mais il a peut-??tre ??t?? la suite d'une utilisation li??e par Helmholtz. "Eigen" peut ??tre traduit comme "propre", "propre ??", "caract??ristique" ou "individuelle" -emphasizing l'importance de valeurs propres sont de d??finir la nature unique d'une transformation sp??cifique. Depuis quelque temps, le terme standard en anglais ??tait "valeur ad??quate", mais le terme le plus distinctif "valeur propre" est aujourd'hui la norme.
Le premier algorithme num??rique pour calculer les valeurs propres et les vecteurs propres est apparu en 1929, lorsque Von Mises a publi?? le Proc??d?? d'alimentation. Une des m??thodes les plus populaires aujourd'hui, le Algorithme QR, a ??t?? propos?? ind??pendamment par Francis et Kublanovskaya en 1961.
D??finitions: l'??quation aux valeurs propres
Transformations lin??aires d'un espace vectoriel, tels que rotation, r??flexion, ??tirage, compression, cisaillement ou une combinaison de ceux-ci, peuvent ??tre visualis??es par l'effet qu'ils produisent sur des vecteurs . En d'autres termes, ce sont des fonctions vectorielles. Plus formellement, dans un espace vectoriel L une fonction vecteur A est d??fini si, pour chaque vecteur x de L correspond un vecteur unique, y = A (x) de L. Par souci de concision, les parenth??ses autour du vecteur sur lequel la transformation est int??rim sont souvent omis. Une fonction de vecteur A est lin??aire si elle a les deux propri??t??s suivantes:
- additivit??
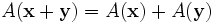
- homog??n??it??

o?? x et y sont tous deux des vecteurs de l'espace vectoriel et α L est ne importe quel nombre r??el . Une telle fonction est diversement appel?? une transformation lin??aire, op??rateur lin??aire, ou lin??aire endomorphisme sur l'espace L.
Compte tenu d'une transformation lin??aire A, un vecteur non nul x est d??fini comme ??tant un vecteur propre de la transformation se il satisfait ?? l'??quation de valeur propre λ = A x x pour une λ scalaire. Dans cette situation, le scalaire λ est appel?? une valeur propre de A correspondant au vecteur propre x. |
L'??quation cl?? dans cette d??finition est l'??quation aux valeurs propres, A x = λ x. La plupart des vecteurs x ne seront pas satisfaire une telle ??quation. Un vecteur typique x change de direction lorsque sollicit?? par un, de sorte que A x ne est pas un multiple de x. Cela signifie que seulement certains vecteurs sont des vecteurs propres sp??cifiques x, et seuls certains num??ros sp??ciaux sont les valeurs propres λ. Bien s??r, si A est un multiple de la matrice d'identit??, alors aucun vecteur change de direction et tous les vecteurs non nuls sont des vecteurs propres. Mais dans le cas d'habitude, vecteurs propres sont rares et espac??es. Ce sont les "modes normaux?? du syst??me, et ils agissent de fa??on ind??pendante.
L'exigence que le vecteur propre non nulle est impos??e parce que l'??quation A 0 = λ 0 d??tient pour chaque A et chaque λ. Depuis l'??quation est toujours trivialement vrai, ce ne est pas un cas int??ressant. En revanche, une valeur propre peut ??tre ??gal ?? z??ro de mani??re non triviale. Une valeur propre peut ??tre, et est g??n??ralement, ??galement un nombre complexe . Dans la d??finition donn??e ci-dessus, les vecteurs propres et les valeurs propres ne se produisent pas de fa??on ind??pendante. Au lieu de cela, chaque vecteur propre est associ?? ?? une valeur propre sp??cifique. Pour cette raison, et x un vecteur propre d'une valeur propre λ correspondant sont souvent d??sign??s en tant que eigenpair. Une valeur propre peut ??tre associ?? ?? plusieurs ou m??me avec un nombre infini de vecteurs propres. Mais ?? l'inverse, si un vecteur propre est donn??, la valeur propre associ??e ?? ce vecteur propre est unique. En effet, de l'??galit?? A x = λ x = λ 'x et de x ≠ 0, il se ensuit que λ = λ.

G??om??triquement (Fig. 2), l'??quation de valeur propre signifie que, dans la transformation des vecteurs propres d'une exp??rience seulement des changements dans amplitude et le signe - la direction de A x est la m??me que celle de x. Ce type de transformation lin??aire est d??fini comme ??tant homoth??tie (dilatation, la transformation similitude). La valeur propre λ est simplement la quantit?? de ????tirer?? ou ??psy?? ?? laquelle un vecteur est soumis lorsqu'il est transform?? par A. Si λ = 1, le vecteur reste inchang?? (affect?? par la transformation). Une transformation I dans laquelle un vecteur x reste inchang??, I x = x, est d??finie comme transformation d'identit??. Si λ = -1, le vecteur retourne dans la direction oppos??e (tourne ?? 180 ??); ce est d??finie comme r??flexion.
Si x est un vecteur propre de la transformation lin??aire A avec λ valeur propre, alors tout vecteur y = α x est aussi un vecteur propre de A avec la m??me valeur propre. De l'homog??n??it?? de la transformation A il en r??sulte que α = A y (A x) = α (λ x) = λ (α x) = λ y. De m??me, en utilisant la propri??t?? d'additivit?? de la transformation lin??aire, il peut ??tre d??montr?? que toute combinaison lin??aire des vecteurs propres de valeur propre λ a la m??me valeur propre λ. Par cons??quent, tout vecteur non-z??ro dans la ligne passant par x et le vecteur nul est un vecteur propre avec la m??me valeur propre que x. Avec le vecteur nul, ces vecteurs propres forment un sous-espace de l'espace vectoriel appel?? un espace propre. Les vecteurs propres correspondant ?? diff??rentes valeurs propres sont lin??airement sens ind??pendante, en particulier, que dans un espace de dimension n la transformation lin??aire A ne peut pas avoir plus de n vecteurs propres avec diff??rentes valeurs propres. Les vecteurs de l'espace propre de g??n??rer un sous-espace lin??aire de A qui est invariant (inchang??) en vertu de cette transformation.
Si un base est d??fini dans l'espace vectoriel L n, tous les vecteurs peuvent ??tre exprim??es en termes de composants . Vecteurs polaires peuvent ??tre repr??sent??s comme une matrice-colonne ?? n lignes, o?? n est le nombre de dimensions de l'espace. Transformations lin??aires peuvent ??tre repr??sent??s avec des matrices carr??es; ?? chaque transformation lin??aire A de L n correspond une matrice carr??e de rang n. Inversement, ?? chaque matrice carr??e de rang n correspond une transformation lin??aire de L n ?? une base donn??e. En raison de l'additivit?? et l'homog??n??it?? du trasformation lin??aire et l'??quation aux valeurs propres (qui est aussi une transformation lin??aire - homoth??tie), ces fonctions vectorielles peuvent ??tre exprim??es sous forme de matrice. Ainsi, dans l'un vecteur bidimensionnel espace L 2 ??quip?? base standard, l'??quation de vecteur propre pour une transformation lin??aire A peut ??tre ??crit dans la repr??sentation matricielle suivante:
o?? la juxtaposition des matrices signifie la multiplication de matrices . Ceci est ??quivalent ?? un ensemble de n ??quations lin??aires, o?? n est le nombre de vecteurs de base de la base indiqu??e. Dans ces ??quations ?? la fois la valeur propre λ de et les composantes de x sont inconnues Variables.
Les vecteurs propres de A tels que d??finis ci-dessus sont ??galement appel??s vecteurs propres ?? droite parce qu'ils sont des vecteurs colonnes qui se dressent sur le c??t?? droit de la matrice A dans l'??quation aux valeurs propres. Se il existe une matrice transpos??e A T Statisfait que l'??quation de valeur propre, qui est, si A = T x λ x, alors x T = λ (λ x) = T (A T x) = x T T A, T ou X A = λ x T. La derni??re ??quation est similaire ?? l'??quation aux valeurs propres mais au lieu de le vecteur colonne x il contient son vecteur transpos??, le vecteur ligne x T, qui se dresse sur le c??t?? gauche de la matrice A. Les vecteurs propres qui satisfont l'??quation x valeur propre T A = λ x T sont appel??s vecteurs propres gauches. Ils sont des vecteurs de rang??e. Dans de nombreuses applications communes, seuls vecteurs propres ?? droite doivent ??tre consid??r??s. D'o?? le terme absolu "vecteur propre?? peut ??tre compris comme se r??f??rant ?? un vecteur propre droit. ??quations aux valeurs propres, ??crites en termes de vecteurs propres ?? droite ou ?? gauche (A x = λ x et x T x A = λ T) ont la m??me valeur propre λ.
Un vecteur propre est d??fini comme ??tant un principal ou vecteur propre dominante si elle correspond ?? la valeur propre de plus grande amplitude (pour nombres r??els, la plus grande valeur absolue). L'application r??p??t??e d'une transformation lin??aire pour un r??sultat de vecteurs arbitraires dans un vecteur proportionnel (colin??aires) au vecteur propre capital.
L'applicabilit?? l'??quation de valeur propre ?? la th??orie de la matrice g??n??rale ??tend l'utilisation de vecteurs et valeurs propres ?? toutes les matrices, et donc grandement ??tend le champ d'utilisation de ces constructions math??matiques non seulement ?? des transformations dans les espaces vectoriels lin??aires mais ?? tous les domaines de la science qui utilisent des matrices: ??quations lin??aires syst??mes, optimisation, vecteur et calcul tensoriel, tous les domaines de la physique qui utilisent des quantit??s de matrice, la physique quantique, la relativit?? en particulier, et de l'??lectrodynamique, ainsi que de nombreuses applications d'ing??nierie.
??quation caract??ristique
La d??termination des valeurs et vecteurs propres est important dans pratiquement tous les domaines de la physique et de nombreux probl??mes d'ing??nierie, comme des calculs de stress, analyse de la stabilit??, des oscillations des syst??mes vibrants, etc. Il est ??quivalent ?? diagonalisation des matrices, et est la premi??re ??tape d'orthogonalisation, trouver des invariants, l'optimisation (minimisation ou la maximisation), l'analyse des syst??mes lin??aires, et de nombreuses autres applications courantes.
La m??thode habituelle de trouver tous les vecteurs et valeurs propres d'un syst??me est le premier ?? se d??barrasser des ??l??ments inconnus des vecteurs propres, puis de trouver les valeurs propres, branchez ceux qui reviennent un par un dans l'??quation aux valeurs propres sous forme de matrice et r??soudre ce comme un syst??me de ??quations lin??aires pour trouver les composantes des vecteurs propres. De la transformation d'identit?? I x = x, o?? I est la matrice d'identit??, x dans l'??quation de valeur propre peut ??tre remplac??e par I x ?? envoyer:
La matrice d'identit?? est n??cessaire pour maintenir les matrices, vecteurs et scalaires droite; l'??quation (A - λ) x = 0 est plus courte, mais m??lang?? car il ne fait pas de distinction entre la matrice, scalaire et vectoriel. L'expression dans le c??t?? droit est transf??r?? vers le c??t?? gauche avec un signe n??gatif, laissant 0 sur le c??t?? droit:
Le vecteur propre x est tir?? derri??re parenth??ses:
Cela peut ??tre consid??r?? comme un syst??me d'??quations lin??aires dans lequel la matrice de coefficients est l'expression entre parenth??ses, la matrice des inconnues est x, et la matrice de droite est nul. Selon La r??gle de Cramer, ce syst??me d'??quations a des solutions non triviales (pas tous des z??ros, ou pas de nombre) si et seulement si son d??terminant dispara??t, de sorte que les solutions de l'??quation sont donn??s par:
Cette ??quation est d??finie comme la ??quation caract??ristique (moins souvent, ??quation s??culaire) de A, et le c??t?? gauche est d??finie comme la polyn??me caract??ristique. Le vecteur propre x ou de ses composants ne sont pas pr??sents dans l'??quation caract??ristique, de sorte ?? ce stade, ils sont supprim??s, et les seules inconnues qui restent ?? ??tre calcul?? sont les valeurs propres (les composants de la matrice A sont donn??s, i. E, su ?? l'avance ). Pour un espace vectoriel L 2, la transformation A est une matrice carr??e 2 ?? 2, et l'??quation caract??ristique peut ??tre ??crit sous la forme suivante:
Expansion du d??terminant dans les r??sultats de c??t?? gauche dans un polyn??me caract??ristique qui est un Monic (son coefficient de premier plan est une) polynomiale de la seconde degr??, et l'??quation caract??ristique est la ??quation quadratique
qui a les solutions suivantes ( racines):
Pour les matrices r??elles, les coefficients du polyn??me caract??ristique sont toutes r??elles. Le nombre et le type des racines d??pend de la valeur de la discriminante, D. Pour les cas D = 0, D> 0, ou D <0, respectivement, les racines sont une r??alit??, deux r??el, deux ou complexe. Si les racines sont complexes, ils sont aussi complexes conjugu??s de l'autre. Lorsque le nombre de racines est inf??rieur au degr?? du polyn??me caract??ristique (ce dernier est aussi le rang de la matrice, et le nombre de dimensions de l'espace vectoriel) l'??quation a une racine multiple. Dans le cas d'une ??quation quadratique avec une racine, cette racine est une racine double, ou avec une racine 2. Une multiplicit?? racine avec une multiplicit?? de 1 est une racine simple. Une ??quation quadratique avec deux racines r??elles ou complexes a des racines simples. En g??n??ral, la alg??brique multiplicit?? d'une valeur propre est d??finie comme la multiplicit?? correspondante de la racine du polyn??me caract??ristique. Le spectre d'une transformation sur une dimension finie espace vectoriel est d??fini comme le ensemble de toutes ses valeurs propres. Dans le cas de dimension infinie, le concept de spectre est plus subtile et d??pend de la topologie de l'espace vectoriel.
La formule g??n??rale pour le polyn??me caract??ristique d'une matrice de n est -carr??
o?? S 0 = 1, S 1 = tr (A), le trace de la matrice de transformation A, et S k avec k> 1 sont les sommes du principal mineurs d'ordre k. Le fait que les valeurs propres sont racines d'une ??quation n -condamner montre qu'une transformation lin??aire d'un espace lin??aire de dimension n a au plus n valeurs propres diff??rentes. Selon le th??or??me fondamental de l'alg??bre, dans un espace lin??aire complexe, le polyn??me caract??ristique a au moins un z??ro. Par cons??quent, toute transformation lin??aire d'un espace lin??aire complexe comporte au moins une valeur propre. Pour les espaces lin??aires r??els, si la dimension est un nombre impair, la transformation lin??aire a au moins une valeur propre; si la dimension est un nombre pair, le nombre de valeurs propres d??pend du d??terminant de la matrice de transformation: si le d??terminant est n??gatif, il existe au moins l'une positive et une valeur propre n??gative, si le d??terminant ne est rien positive peut ??tre dit ?? propos de l'existence de valeurs propres. La complexit?? du probl??me de trouver des racines / valeurs propres de la caract??ristique augmente rapidement avec l'augmentation du polyn??me du degr?? du polyn??me (la dimension de l'espace vectoriel), n. Ainsi, pour n = 3, les valeurs propres sont des racines de la ??quation cubique, pour n = 4 - racines de la ??quation quartique. Pour n> 4, il n'y a pas de solutions exactes et il faut recourir ?? des algorithmes de profondes enqu??te, comme la m??thode de Newton ( La m??thode de Horner) pour trouver des approximations num??riques de valeurs propres. Pour les grandes sym??trique matrices creuses, Lanczos algorithme est utilis?? pour calculer des valeurs propres et des vecteurs propres.
Afin de trouver les vecteurs propres, les valeurs propres ainsi trouv??s que les racines des ??quations caract??ristiques sont branch??s en arri??re, un ?? la fois, dans l'??quation aux valeurs propres ??crite dans une forme de matrice (illustr??s pour le cas le plus simple d'un ?? deux dimensions espace vectoriel L 2 ):
o?? λ est l'une des valeurs propres trouv??es comme une racine de l'??quation caract??ristique. Cette ??quation matricielle est ??quivalent ?? un syst??me de deux ??quations lin??aires:
Les ??quations sont r??solues pour x et y par les m??thodes alg??briques ou matrice habituels. Souvent, il est possible de diviser les deux c??t??s des ??quations ?? une ou plusieurs des coefficients qui rend certains des coefficients devant les inconnues ??gal ?? 1. Ceci est appel?? normalisation des vecteurs, et correspond ?? choisir l'un des vecteurs propres (le vecteur propre normalis??) comme repr??sentatif de tous les vecteurs dans l'espace propre correspondant ?? la valeur propre respective. X et Y sont ainsi trouv?? les composantes du vecteur propre dans le syst??me de coordonn??es utilis?? (le plus souvent cart??sien ou polaire).
En utilisant le Cayley-Hamilton th??or??me qui stipule que chaque matrice carr??e satisfait sa propre ??quation caract??ristique, il peut ??tre d??montr?? que (le plus g??n??ralement, dans l'espace complexe), il existe au moins un vecteur non nul qui satisfait l'??quation aux valeurs propres ?? cette matrice. Comme il a ??t?? dit dans la section D??finitions, ?? chaque valeur propre correspond un nombre infini de colin??aires vecteurs propres (lin??airement d??pendants) qui forment l'espace propre pour cette valeur propre. D'autre part, la dimension de l'espace propre est ??gal au nombre de vecteurs propres lin??airement ind??pendants qu'il contient. La multiplicit?? g??om??trique d'une valeur propre est d??finie comme la dimension de l'espace propre associ??. Une valeur propre multiple peut donner lieu ?? un seul vecteur propre de telle sorte que sa multiplicit?? alg??brique peut ??tre diff??rente de la multiplicit?? g??om??trique. Cependant, comme d??j?? dit, les diff??rentes valeurs propres sont appari??s avec les vecteurs propres lin??airement ind??pendants. De ce qui pr??c??de, il r??sulte que la multiplicit?? g??om??trique ne peut pas ??tre sup??rieure ?? la multiplicit?? alg??brique.
Par exemple, un vecteur propre d'une rotation en trois dimensions est un vecteur situ?? dans la l'axe autour duquel se effectue la rotation. La valeur propre correspondante est 1 et l'espace propre correspondant contient tous les vecteurs long de l'axe. Comme il se agit d'un espace ?? une dimension, sa multiplicit?? g??om??trique est une. Ce est la seule valeur propre du spectre (de cette rotation) qui est un nombre r??el .
Exemples
Les exemples qui suivent sont pour le cas le plus simple de vecteur ?? deux dimensions espace L 2 mais ils peuvent facilement ??tre appliqu??es de la m??me mani??re ?? des espaces de dimensions sup??rieures.
Homoth??tie, l'identit??, le point de r??flexion et de transformation nulle
En unidimensionnel espace vectoriel L 1, envisager une cha??ne de caoutchouc li?? au soutien immobile dans une extr??mit??, comme celle sur la fronde d'un enfant. Tirer la corde loin du point d'attache se ??tend et se allonge par un facteur d'??chelle λ qui est un nombre r??el. Chaque vecteur de la corde est tendue de fa??on ??gale, avec le m??me facteur d'??chelle λ, et m??me si elle conserve allong?? sa direction d'origine. Ce type de transformation est appel?? homoth??tie (transformation de similitude). Pour un espace vectoriel ?? deux dimensions L 2, envisager une feuille de caoutchouc ??tir?? dans toutes les directions comme une petite zone de la surface d'un ballon ?? gonfler (Fig. 3). Tous les vecteurs qui proviennent d'un point fixe sur la surface du ballon sont ??tir??es aussi avec le m??me facteur d'??chelle λ. La transformation de homoth??tie en deux dimensions est d??crit par une matrice carr??e 2 ?? 2, agissant sur un vecteur arbitraire dans le plan de la / surface r??tr??cissement ??tirement. Apr??s avoir fait la multiplication de la matrice, on obtient:
qui, exprim??e en termes, signifie que la transformation est ??quivalent ?? la multiplication de la longueur du vecteur par λ tout en conservant son orientation d'origine. L'??quation ainsi obtenue est exactement l'??quation aux valeurs propres. Depuis le vecteur prise ??tait arbitraire, dans toute homoth??tie vecteur dans l'espace vectoriel subit l'??quation aux valeurs propres, ce est ?? dire tout vecteur couch?? sur la surface du ballon peut ??tre un vecteur propre. Si la transformation est l'??tirement (??longation, l'extension, l'inflation), ou de r??tr??cissement (compression, la d??flation) d??pend du facteur d'??chelle: si λ> 1, il se ??tire, si λ <1, il se r??tr??cit.
Plusieurs autres transformations peuvent ??tre consid??r??es comme des types sp??ciaux de homoth??tie de certains, valeur constante fixe de λ: dans l'identit?? qui laisse inchang??e vecteurs, λ = 1; en r??flexion autour d'un point qui pr??serve la longueur et la direction des vecteurs mais modifie leur orientation oppos??e ?? celle, λ = -1; et en transformation nulle qui transforme chaque vecteur au vecteur nul, λ = 0. La transformation nulle ne donne pas lieu ?? un vecteur propre ??tant donn?? que le vecteur nul ne peut ??tre un vecteur propre mais il a depuis espace propre espace propre contient aussi le vecteur nul par d??finition.
Mise ?? l'??chelle in??gale
Pour un exemple un peu plus compliqu??, envisager une feuille qui est ??tir?? uneqally dans deux directions perpendiculaires le long des axes de coordonn??es, ou, de m??me, ??tir?? dans une direction, et diminu?? dans l'autre sens. Dans ce cas, il existe deux facteurs d'??chelle diff??rents: k 1, pour la mise ?? l'??chelle dans la direction x et k 2 pour la mise ?? l'??chelle dans la direction y. La matrice de transformation est  Et l'??quation caract??ristique est λ 2 - λ (k 1 + k 2) + k 1 k 2 = 0. Les valeurs propres, obtenu comme racines de cette ??quation sont λ 1 = k 1 et λ 2 = k 2 signifie, comme pr??vu, que les deux valeurs propres sont les facteurs d'??chelle dans les deux directions. Branchement k 1 retour dans l'??quation donne une valeur propre des vecteurs propres:
Et l'??quation caract??ristique est λ 2 - λ (k 1 + k 2) + k 1 k 2 = 0. Les valeurs propres, obtenu comme racines de cette ??quation sont λ 1 = k 1 et λ 2 = k 2 signifie, comme pr??vu, que les deux valeurs propres sont les facteurs d'??chelle dans les deux directions. Branchement k 1 retour dans l'??quation donne une valeur propre des vecteurs propres:
En divisant par la derni??re ??quation k 2 - k 1, on obtient y = 0, qui repr??sente l'axe x. Un vecteur de longueur 1 prise le long de cet axe repr??sente le vecteur propre normalis?? correspondant ?? la valeur propre λ 1. Le vecteur propre correspondant ?? λ 2 qui est un vecteur unitaire le long de l'axe des y se trouve d'une mani??re similaire. Dans ce cas, les deux valeurs propres sont simples (avec alg??brique et multiplicit??s g??om??triques ??gal ?? 1). Selon les valeurs de λ 1 et λ 2, il existe plusieurs cas particuliers notables. En particulier, si λ 1> 1 et λ 2 = 1, la transformation est un ??tirement dans la direction de l'axe x. Si λ 2 = 0, 1 et λ = 1, la transformation est une projection de la surface L 2 sur l'axe x, car tous les vecteurs dans la direction de y deviennent vecteurs nuls.
Que la feuille de caoutchouc est tendue le long de l'axe x (k 1> 1) et simultan??ment r??tr??ci le long de l'axe y (k 2 <1) comme sur la Fig. 4. Puis λ = 1 k 1 aura la valeur propre principale. Application r??p??t??e cette transformation d'??tirement / contraction de nombreuses fois ?? la feuille de caoutchouc tournera ce dernier de plus en plus semblable ?? une cha??ne de caoutchouc. Tout vecteur sur la surface de la feuille de caoutchouc sera orient?? de proche en proche ?? la direction de l'axe x (la direction d'??tirage), ce est-il deviendra colin??aire avec le vecteur propre principale.
Cisaille
Dans le plan de cisaillement est une transformation dans laquelle tous les points le long d'une ligne donn??e restent fixes alors que les autres points sont d??cal??s parall??lement ?? cette ligne d'une distance proportionnelle ?? leur distance perpendiculaire de la ligne. Contrairement ??chelle, cisaillement une figure plane ne change pas son domaine. Cisaillement peut ??tre horizontale - le long de l'axe X, ou vertical - le long de l'axe Y. Dans cisaillement horizontal (Fig. 5), un point P de l'avion se d??place parall??lement ?? l'axe X ?? l'endroit P 'de sorte que sa coordonn??e Y ne change pas alors que le x incr??ments pour devenir coordonn??e x' = x + k, o?? k est appel?? facteur de cisaillement. Le facteur de cisaillement est proportionnelle ?? y et ?? l'angle φ cisaillement: k = x '- x = y φ de lit b??b??. La matrice d'une transformation de cisaillement horizontal est  . L'??quation caract??ristique est λ 2 - 2 λ + 1 = (1 - λ) 2 = 0, qui a une seule racine λ = 1. Par cons??quent, la valeur propre λ = 1 est multiple avec multiplicit?? alg??brique 2. Le vecteur propre (s) se trouvent sous forme de solutions de
. L'??quation caract??ristique est λ 2 - 2 λ + 1 = (1 - λ) 2 = 0, qui a une seule racine λ = 1. Par cons??quent, la valeur propre λ = 1 est multiple avec multiplicit?? alg??brique 2. Le vecteur propre (s) se trouvent sous forme de solutions de
La derni??re ??quation est divis?? par k (normalisation) pour obtenir y = 0, qui est une ligne droite le long de l'axe x. Cette ligne repr??sente l'espace propre ?? une dimension. Dans le cas d'un cisaillement de la multiplicit?? alg??brique de la valeur propre (2) est inf??rieure ?? sa multiplicit?? g??om??trique (1, la dimension de l'espace propre). Le vecteur propre est un vecteur unitaire le long de l'axe x. Le cas de cisaillement vertical avec matrice de transformation 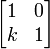 est trait??e de la m??me fa??on; le vecteur propre au cisaillement vertical est le long de l'axe y. L'application de la transformation ?? plusieurs reprises cisaillement change la direction de ne importe quel vecteur dans le plan de proche en proche ?? la direction du vecteur propre.
est trait??e de la m??me fa??on; le vecteur propre au cisaillement vertical est le long de l'axe y. L'application de la transformation ?? plusieurs reprises cisaillement change la direction de ne importe quel vecteur dans le plan de proche en proche ?? la direction du vecteur propre.
Rotation

Un rotation dans un plan est une transformation qui d??crit le mouvement d'un corps rigide (ou vecteur) autour d'un point fixe. Avec l'aide de fonctions trigonom??triques, la rotation peut ??tre d??crite comme une transformation lin??aire. Les ??l??ments d'une matrice de rotation repr??sentent les composantes du vecteur rotation. Ainsi, un sens inverse des aiguilles d'une rotation de coordonn??es, un vecteur ou plan sur l'origine d'un angle φ de sorte que les coordonn??es x et y de changement x 'et y' sont d??crits par le syst??me d'??quations lin??aires suivant:
ou, en termes de matrices et des vecteurs de colonnes:
L'??quation caract??ristique de la matrice de transformation 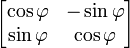 est λ 2 - 2λ cos φ + 1 = 0. Cette ??quation quadratique a un discriminant D = 4 (2 cos φ - 1) = - 4 sin 2 φ qui est un nombre n??gatif pour φ ≠ 0 ?? et 180 ?? φ ≠ ?? k avec k impair. Par cons??quent, sauf pour ces derniers cas sp??ciaux, racines r??elles (valeurs propres) ne existent pas pour la rotation. L'??quation caract??ristique a deux racines complexes λ 1 et λ 2, qui sont des conjugu??s complexes de l'autre:
est λ 2 - 2λ cos φ + 1 = 0. Cette ??quation quadratique a un discriminant D = 4 (2 cos φ - 1) = - 4 sin 2 φ qui est un nombre n??gatif pour φ ≠ 0 ?? et 180 ?? φ ≠ ?? k avec k impair. Par cons??quent, sauf pour ces derniers cas sp??ciaux, racines r??elles (valeurs propres) ne existent pas pour la rotation. L'??quation caract??ristique a deux racines complexes λ 1 et λ 2, qui sont des conjugu??s complexes de l'autre:
Ces deux racines sont les deux valeurs propres de rotation chacune avec une multiplicit?? alg??brique ??gal ?? 1. Brancher la premi??re valeur propre, λ 1, de retour dans l'??quation aux valeurs propres donne le premier vecteur propre:
D'autres exemples
Comme la Terre tourne, chaque flèche pointant vers l'extérieur depuis le centre de la Terre tourne également, à l'exception des flèches qui sont parallèles à l'axe de rotation. Considérez la transformation de la Terre après une heure de rotation: Une flèche du centre de la Terre à la Geographic Pôle Sud serait un vecteur propre de cette transformation, mais une flèche du centre de la Terre à n'importe où sur le équateur ne serait pas un vecteur propre. Depuis la flèche pointant vers le pôle est pas étirée par la rotation de la Terre, sa valeur propre est 1.

Cependant, l'espace géométrique tridimensionnel est pas le seul espace vectoriel. Par exemple, considérons une corde souligné fixe aux deux extrémités, comme les cordes vibrantes d'un instrument à cordes (Fig. 2). Les distances des atomes de la corde vibrante à partir de leurs positions lorsque la corde est au repos peuvent être considérées comme les composantes d'un vecteur dans un espace à autant de dimensions qu'il ya atomes dans le câble.
Supposons que la corde est un milieu continu. Si l'on considère l'équation pour l' accélération à chaque point de la corde, ses vecteurs propres, ou de fonctions propres , sont les ondes stationnaires. Les ondes stationnaires correspondent à des oscillations particulières de la corde de telle sorte que l'accélération de la corde est tout simplement sa forme réduite par un facteur de ce facteur, la valeur propre, se révèle être  o??
o?? 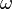 est le la fréquence angulaire de l'oscillation. Chaque composante du vecteur associé à la corde est multiplié par un facteur dépendant du temps
est le la fréquence angulaire de l'oscillation. Chaque composante du vecteur associé à la corde est multiplié par un facteur dépendant du temps  . Si d'amortissement est considéré, la amplitude de cette oscillation diminue jusqu'à ce que la corde arrête oscillant, ce qui correspond à un complexe ??. On peut alors associer une vie avec la partie imaginaire de ??, et concernent le concept d'un vecteur propre à la notion de r??sonance. sans amortissement, le fait que l'opérateur d'accélération (en supposant une densité uniforme) est conduit hermitiques à plusieurs propriétés importantes, comme celle les modèles de vagues permanentes sont des fonctions orthogonales.
. Si d'amortissement est considéré, la amplitude de cette oscillation diminue jusqu'à ce que la corde arrête oscillant, ce qui correspond à un complexe ??. On peut alors associer une vie avec la partie imaginaire de ??, et concernent le concept d'un vecteur propre à la notion de r??sonance. sans amortissement, le fait que l'opérateur d'accélération (en supposant une densité uniforme) est conduit hermitiques à plusieurs propriétés importantes, comme celle les modèles de vagues permanentes sont des fonctions orthogonales.
Fonctions propres
Cependant, il est parfois contre nature, voire impossible d'écrire l'équation aux valeurs propres dans une forme de matrice. Cela se produit par exemple lorsque l'espace vectoriel de dimension infinie est, par exemple, dans le cas de la corde au-dessus. Selon la nature de la transformation T et l'espace à laquelle il est applicable, il peut être avantageux pour représenter l'équation de valeur propre comme un ensemble d' équations différentielles . Si T est un opérateur différentiel, les vecteurs propres sont communément appelés fonctions propres de l'opérateur différentiel représentant T . Par exemple, différenciation lui-même est une transformation linéaire depuis
(f(t) etg(t) sont desfonctions différentiables, etunetbsont desconstantes).
Envisager la différenciation par rapport à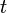 .ses fonctions propresh(t) obéir à l'équation aux valeurs propres:
.ses fonctions propresh(t) obéir à l'équation aux valeurs propres:
 ,
,
où ?? est la valeur propre associée à la fonction. Une telle fonction du temps est constant si  , croît proportionnellement à lui-même si
, croît proportionnellement à lui-même si 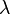 est positif, et se désintègre proportionnellement à lui-même si
est positif, et se désintègre proportionnellement à lui-même si 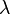 est négatif. Par exemple, une population de lapins idéalisée se reproduit autant plus vite que les lapins, il ya, et donc satisfait à l'équation avec un lambda positif.
est négatif. Par exemple, une population de lapins idéalisée se reproduit autant plus vite que les lapins, il ya, et donc satisfait à l'équation avec un lambda positif.
La solution de l'équation de valeur propre est 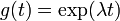 , la fonction exponentielle ; ainsi que la fonction est une fonction propre de l'opérateur différentiel d / dt à la valeur propre ?? . Si ?? est négative , nous appelons l'évolution de g un de décroissance exponentielle; si il est positif , une croissance exponentielle . La valeur de ?? peut être tout nombre complexe . Le spectre de d / dt est par conséquent tout le plan complexe . Dans cet exemple, l'espace de vecteur dans lequel l'opérateur d / dt agit est l'espace des fonctions différentiables d'une variable. Cet espace a une dimension infinie (car il est impossible d'exprimer toute fonction différentiable comme une combinaison linéaire d'un nombre fini de fonctions de base). Cependant, l'espace propre associé à une valeur propre donnée ?? est unidimensionnel. Il est l'ensemble de toutes les fonctions
, la fonction exponentielle ; ainsi que la fonction est une fonction propre de l'opérateur différentiel d / dt à la valeur propre ?? . Si ?? est négative , nous appelons l'évolution de g un de décroissance exponentielle; si il est positif , une croissance exponentielle . La valeur de ?? peut être tout nombre complexe . Le spectre de d / dt est par conséquent tout le plan complexe . Dans cet exemple, l'espace de vecteur dans lequel l'opérateur d / dt agit est l'espace des fonctions différentiables d'une variable. Cet espace a une dimension infinie (car il est impossible d'exprimer toute fonction différentiable comme une combinaison linéaire d'un nombre fini de fonctions de base). Cependant, l'espace propre associé à une valeur propre donnée ?? est unidimensionnel. Il est l'ensemble de toutes les fonctions 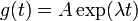 , où A est une constante arbitraire, la population initiale à t = 0 .
, où A est une constante arbitraire, la population initiale à t = 0 .
Théorème spectral
Dans sa version la plus simple, les Etats théorème spectral que, sous certaines conditions, une transformation linéaire d'un vecteur v peut être exprimée comme une combinaison linéaire des vecteurs propres, dans lequel le coefficient de chaque vecteur propre est égale à la fois valeur propre correspondante l' produits scalaire (ou produit scalaire) du vecteur propre avec le vecteur v . Mathématiquement, on peut écrire:
où v 1 , v 2 , ... et ?? 1 , ?? 2 , ... stand pour les vecteurs propres et les valeurs propres de T . Le théorème est valable pour toutes les transformations linéaires auto-adjoints (transformations linéaires donnés par de véritables matrices symétriques et matrices hermitiennes), et pour la classe plus générale de ( complexes ) matrices normales.
Si l'on définit le n de la puissance de la transformation à la suite de l'appliquer n fois de suite, on peut également définir des polynômes de transformations. Une version plus générale du théorème est que tout polynôme P de T est donnée par
Le théorème peut être étendu à d'autres fonctions de transformations, telles queles fonctions analytiques, le cas le plus général étantfonctions Borel.
Eigendecomposition
Le théorème spectral pour les matrices peut être énoncé comme suit. Soit A un carré n × n matrice. Soit q 1 ... q k soit une base de vecteurs propres, à savoir un ensemble indexé de k vecteurs propres linéairement indépendants, où k est la dimension de l'espace engendré par les vecteurs propres de A . Si k = n , alors A peut être écrite
oùQest le carrén×nmatrice dont lesième colonne est le vecteur propre baseq jedeAet??est lamatrice diagonale dont la diagonale éléments sont les valeurs propres correspondantes, à savoir?? je je= ??je.
Des espaces de dimension infinie
Si l'espace vectoriel de dimension infinie est un espace de Banach, la notion de valeurs propres peut être généralisée à la notion de spectre. Le spectre est l'ensemble des scalaires ?? pour laquelle ( T - ??) -1 est pas défini; qui est, de sorte que T - ?? n'a pas borné inverse.
Il est clair que si ?? est une valeur propre de T , ?? est dans la gamme de T . En général, l'inverse est impossible. Il existe des opérateurs sur Hilbert ou espaces de Banach qui ne disposent pas du tout des vecteurs propres. Ceci peut être vu dans l'exemple suivant. Le décalage bilatéral sur l'espace de Hilbert ??? 2 ( Z ) (autrement dit, l'espace de toutes les séquences de scalaires ... un -1 , un 0 , un 1 , un 2 , ... de telle sorte que
converge) n'a pas de valeur propre mais il a des valeurs spectrales.
Dans les espaces de dimension infinie, le spectre d'un opérateur borné est toujours non vide. Cela est également vrai pour un illimitée opérateur auto adjoint. Via ses mesures spectrales, le spectre d'un opérateur auto-adjoint, bornés ou non, peut être décomposé en absolument continue, pur point, et des pièces singulières. (Voir La décomposition du spectre.)
Fonctions exponentielles sont fonctions propres de l'opérateur de dérivée (la dérivée de fonctions exponentielles sont proportionnelles à themself). La croissance exponentielle et décroissance fournissent donc des exemples de spectres continus, de même que l'exemple de corde vibrante illustré ci-dessus. Le atome d'hydrogène est un exemple où les deux types de spectres apparaîtra. Les fonctions propres de l' hamiltonien d'un atome d'hydrogène sont appelés états propres et sont regroupés en deux catégories. Le états liés de l'atome d'hydrogène correspondent à la partie discrète du spectre (ils ont un ensemble discret de valeurs propres qui peut être calculée par la formule Rydberg) tandis que l' ionisation procédés sont décrits par la partie continue (l'énergie de la collision / ionisation non quantifiés).
Applications
Équation de Schrödinger

Un exemple d'une équation aux valeurs propres où la transformationTest représenté en termes d'un opérateur différentiel est le temps-indépendanteéquation de Schrödinger dansla mécanique quantique:
oùH, l'hamiltonien, est un second ordreopérateur différentiel et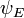 , Le fonction d'onde, est l'une de ses fonctions propres correspondant à la valeur propreE, interprétées comme sonénergie.
, Le fonction d'onde, est l'une de ses fonctions propres correspondant à la valeur propreE, interprétées comme sonénergie.
Toutefois, dans le cas où l'on est intéressé seulement dans les solutions d'État lié de l'équation de Schrödinger, on cherche 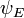 dans l'espace des fonctions de carré intégrable. Depuis cet espace est un espace de Hilbert avec une bien définie produit scalaire, on peut introduire un ensemble de base dans lequel
dans l'espace des fonctions de carré intégrable. Depuis cet espace est un espace de Hilbert avec une bien définie produit scalaire, on peut introduire un ensemble de base dans lequel 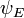 et H peut être représenté comme un tableau à une dimension et une matrice respectivement. Ce permet de représenter l'équation de Schrödinger dans une forme de matrice. (Fig. 4 présente les fonctions propres les plus bas de l' atome d'hydrogène hamiltonien.)
et H peut être représenté comme un tableau à une dimension et une matrice respectivement. Ce permet de représenter l'équation de Schrödinger dans une forme de matrice. (Fig. 4 présente les fonctions propres les plus bas de l' atome d'hydrogène hamiltonien.)
Le Notation de Dirac est souvent utilisé dans ce contexte. Un vecteur, ce qui représente un état ??????du système, dans l'espace de Hilbert des fonctions intégrables carrés est représenté par 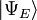 . Dans cette notation, l'équation de Schrödinger est:
. Dans cette notation, l'équation de Schrödinger est:
o?? 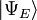 est un état ??????propre de H . C'est un opérateur auto adjoint, l'analogue en dimension infinie des matrices hermitiennes ( voir Observable ). Comme dans le cas de la matrice, dans l'équation ci-dessus
est un état ??????propre de H . C'est un opérateur auto adjoint, l'analogue en dimension infinie des matrices hermitiennes ( voir Observable ). Comme dans le cas de la matrice, dans l'équation ci-dessus  , on entend le vecteur obtenu par application de la transformation H à
, on entend le vecteur obtenu par application de la transformation H à 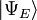 .
.
Orbitales moléculaires
Dans la mécanique quantique , et en particulier dans atomique et moléculaire physique , à l'intérieur de la théorie Hartree-Fock, les atomique et orbitales moléculaires peut être défini par les vecteurs propres de l' opérateur Fock. Les valeurs propres correspondantes sont interprétées comme des potentiels d'ionisation par le théorème de Koopmans. Dans ce cas, le vecteur propre terme est utilisé dans un sens un peu plus générale, étant donné que l'opérateur de Fock est explicitement dépendante des orbitales et leurs valeurs propres. Si l'on veut souligner cet aspect on parle d' équation aux valeurs propres implicite . Ces équations sont généralement résolus par une procédure d'itération, appelée dans ce cas méthode du champ auto-cohérent. Dans la chimie quantique , on représente souvent l'équation de Hartree-Fock dans un non orthogonale base indiqu??e. Cette représentation particulière est un problème aux valeurs propres généralisé appelé équations Roothaan.
Géologie et glaciologie: (Orientation Tensor)
En géologie , en particulier dans l'étude de till glaciaire, vecteurs et valeurs propres sont utilisés comme une méthode par laquelle une masse d'informations de l'orientation et le pendage de les constituants d'un clast tissu peut être résumée dans un espace 3-D de six chiffres. Sur le terrain, un géologue peut recueillir de telles données pour des centaines ou des milliers de fragments dans un échantillon de sol, qui ne peuvent être comparées graphiquement comme dans un Tri-Terrain (Sneed et Folk) diagramme, ou comme un stéréographique sur un Wulff Net . La sortie pour le tenseur d'orientation est dans les trois axes orthogonaux (perpendiculaires) de l'espace. Vecteurs propres sortie de programmes tels que Stereo32 sont dans l'ordre E1> E2> E3, E1 étant l'orientation première de l'orientation clast / immersion, E2 étant le secondaire et E3 étant le tertiaire, en termes de force. L'orientation clast est défini comme le vecteur propre, sur une rose des vents de 360 °. Dip est mesurée comme la valeur propre, le module du tenseur: ce sont évalués à partir de 0 ° (pas dip) à 90 ° (vertical). Diverses valeurs de E1, E2 et E3 signifient des choses différentes, comme on peut le voir dans le livre «Un guide pratique à l'étude de sédiments glaciaires» par Benn & Evans, 2004.
L'analyse factorielle
En l'analyse factorielle, les vecteurs propres d'une matrice de covariance ou de corrélation de la matrice correspondent aux éléments, et les valeurs propres à la variance expliquée par ces facteurs. L'analyse factorielle est une statistique technique utilisée dans les sciences sociales et dans marketing, la gestion des produits, la recherche opérationnelle , et d'autres sciences appliquées qui traitent de grandes quantités de données. L'objectif est d'expliquer la plupart des covariabilité parmi un certain nombre d'observables variables aléatoires en termes d'un plus petit nombre de variables latentes non observables appelées facteurs. Les variables aléatoires observables sont modélisés comme des combinaisons linéaires des facteurs, en plus de termes de variance uniques. Les valeurs propres sont utilisés dans l'analyse utilisé par le logiciel Q-méthodologie; facteurs avec des valeurs propres supérieures à 1,00 sont considérés comme importants, expliquant une quantité importante de la variabilité dans les données, tandis que les valeurs propres inférieures à 1,00 sont considérées comme trop faible, ne pas expliquer une partie significative de la variabilité des données.
Eigenfaces
En traitement d'image, les images traitées de faces peut être considéré comme des vecteurs dont les composantes sont les luminosités de chaque pixel. La dimension de cet espace vectoriel est le nombre de pixels. Les vecteurs propres de la matrice de covariance associée à un grand ensemble d'images normalisées de visages sont appelés eigenfaces; ceci est un exemple d' analyse en composantes principales. Ils sont très utiles pour exprimer toute image de visage comme une combinaison linéaire de certains d'entre eux. Dans le reconnaissance faciale branche de la biométrie, eigenfaces fournir un moyen d'appliquer la compression de données aux visages pour des fins d'identification. Recherche liée aux systèmes de vision propres déterminants gestes de la main ont également été réalisés. Plus sur la détermination de lettres en langue des signes à l'aide propres systèmes peuvent être trouvés ici: http://www.geigel.com/signlanguage/index.php
Semblable à ce concept, les voix propres concept est également développé qui représente la direction générale de la variabilité des prononciations humains d'une énonciation particulière, comme un mot dans une langue. Basé sur une combinaison linéaire de ces voix propres, une nouvelle voix de la prononciation de la parole peut être construit. Ces concepts ont été trouvés utiles dans les systèmes de reconnaissance automatique de la parole, pour l'adaptation au locuteur.
Tenseur d'inertie
En mécanique, les vecteurs propres de latenseur d'inertie définissent lesaxes principaux d'uncorps rigide. Le tenseur inertie est une clé quantité nécessaire pour déterminer la rotation d'un corps rigide autour de soncentre de masse.
Tenseur
En mécanique des solides, le tenseur des contraintes est symétrique et peut donc être décomposé en un tenseur diagonale avec les valeurs propres sur la diagonale et les vecteurs propres comme base. Parce qu'il est diagonale, dans cette orientation, le tenseur des contraintes n'a pas d' éléments de cisaillement; les composants, il ne dispose sont les composantes principales.
Les valeurs propres d'un graphe
En théorie des graphes spectrale, une valeur propre d'un graphe est défini comme une valeur propre de du graphique matrice d'adjacence l'un , ou (de plus en plus) de du graphique matrice de Laplace, qui est soit T - A ou I - T 1/2 AT -1/2 , où T est une matrice support diagonal le degré de chaque sommet, et en T -1/2 , 0 est substitué à 0 -1/2 . Le k ème vecteur propre principal d'un graphe est défini comme étant le vecteur propre correspondant à la k ième plus grande valeur propre de A , ou le vecteur propre correspondant à la k ième plus petite valeur propre du Laplacien. Le premier vecteur propre principal du graphique est également appelée simplement comme le vecteur propre capital.
Le vecteur propre capital est utilisé pour mesurer la centralité de ses sommets. Un exemple est Google l ' algorithme de PageRank. Le vecteur propre principal d'une modification de la matrice de contiguïté du Monde graphique Wide Web donne les rangs de page que ses composants. Ce vecteur correspond à la distribution stationnaire de la chaîne de Markov représenté par la matrice de contiguïté rangée normalisée; Cependant, la matrice d'adjacence doit d'abord être modifié pour assurer une distribution stationnaire existe. Le deuxième vecteur propre principal peut être utilisé pour partitionner le graphique en grappes, par l'intermédiaire de la classification spectrale. D'autres méthodes sont également disponibles pour le clustering.


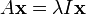

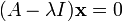
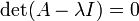
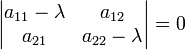

![\ Lambda_ {1,2} = \ frac {1} {2} \ left [(a_ {11} + a_ {22}) \ h \ sqrt {4A_ {12} {21} a_ + (a_ {11} - a_ {22}) ^ 2} \ right].](../../images/149/14952.png)