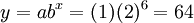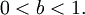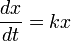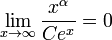Croissance exponentielle
Saviez-vous ...
Enfants SOS offrent un chargement complet de la s??lection pour les ??coles pour une utilisation sur les intranets des ??coles. Parrainage d'enfants aide les enfants du monde en d??veloppement ?? apprendre aussi.
En math??matiques , la croissance exponentielle (ou la croissance g??om??trique) se produit lorsque le taux d'une fonction de croissance est toujours proportionnelle ?? la taille actuelle de la fonction. Cette croissance est dit de suivre une loi exponentielle; le mod??le de croissance exponentielle simple est connu comme le Mod??le de croissance malthusienne. Pour toute quantit?? en croissance exponentielle, plus la quantit?? obtient, plus il grandit. Un dicton alternative est ??Le taux de croissance est proportionnelle ?? l'??tat de la croissance??. La relation entre la taille de la variable d??pendante et son taux de croissance est r??gi par une loi stricte de la forme la plus simple: proportion directe. Il est d??montr?? dans le calcul que cette loi exige que la quantit?? est donn??e par la fonction exponentielle , si nous utilisons l'??chelle de temps correct. Ce qui explique le nom.
Formule de base
Si y conna??t une croissance exponentielle en fonction de x (x ??tant souvent pens??e comme le temps), puis
o?? a est la valeur initiale de Y, ?? savoir une est ce que lorsque y est ??gal ?? x = 0 et b est proportionnelle ?? la vitesse de croissance initiale.
Exemple: Si une esp??ce de bact??ries double tous les dix minutes, ?? partir avec seulement une bact??rie, combien de bact??ries seraient pr??sentes apr??s une heure?
- Apr??s six intervalles (6) 10 minutes, il y aurait 64 bact??ries.
Cela fonctionne ??galement avec d??croissance exponentielle. Dans ce cas, b est inf??rieur ?? 1:
Intuition
La croissance exponentielle de la phrase est souvent utilis?? dans des contextes non techniques pour signifier seulement la croissance ??tonnamment rapide. Dans un sens strictement math??matique, cependant, la croissance exponentielle a un sens pr??cis et ne signifie pas n??cessairement que la croissance va se produire rapidement. En fait, une population peut cro??tre de fa??on exponentielle mais ?? un rythme tr??s lent absolue (comme lorsque l'argent dans un compte bancaire gagne un taux d'int??r??t tr??s bas, par exemple), et peut pousser ??tonnamment rapide sans croissance exponentielle. Et certaines fonctions, telles que la fonction logistique, la croissance exponentielle approximative sur une partie seulement de leur gamme. La section "d??tails techniques" ci-dessous explique exactement ce qui est n??cessaire pour une fonction d'exposer une v??ritable croissance exponentielle.
Mais le principe g??n??ral de la croissance exponentielle est que plus un certain nombre devient, plus vite il se d??veloppe. Toute nombre croissant de fa??on exponentielle finira par se d??velopper plus grand que tout autre nombre qui cro??t ?? un taux constant que pour la m??me quantit?? de temps (et vont aussi se d??velopper plus grand que toute fonction qui ne pousse que subexponentially). Cela est d??montr?? par l'??nigme classique dans lequel un enfant est offert deux choix pour une allocation hebdomadaire de plus en plus: la premi??re option commence ?? 1 cent et double chaque semaine, tandis que la seconde option commence ?? 1 $ et augmente de 1 $ par semaine. Bien que la deuxi??me option, cro??t ?? un taux constant de 1 $ / semaine, paie plus dans le court terme, la premi??re option finalement pousse beaucoup plus grande:
| Semaine | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Option 1 | $ 0,01 | $ 0,02 | $ 0,04 | $ 0,08 | $ 0,16 | $ 0,32 | $ 0,64 | $ 1,28 | $ 2,56 | $ 5,12 | $ 10,24 | $ 20,48 | $ 40,96 | $ 81,92 | $ 163,84 | $ 327,68 | $ 655,36 | $ 1310,72 | $ 2621,44 |
| Option 2 | $ 1 | $ 2 | $ 3 | $ 4 | $ 5 | $ 6 | $ 7 | $ 8 | $ 9 | $ 10 | $ 11 | $ 12 | $ 13 | $ 14 | $ 15 | $ 16 | $ 17 | $ 18 | $ 19 |

Nous pouvons d??crire ces cas math??matiquement. Dans le premier cas, l'allocation ?? la semaine n est 2 n cents; Ainsi, ?? la semaine 15, le paiement est 2 15 = 32768 ?? = $ 327,68. Toutes les formules de la forme k n, o?? k est un nombre immuable sup??rieur ?? 1 (par exemple, 2), et n est la quantit?? de temps ??coul??, cro??tre de fa??on exponentielle. Dans le second cas, le paiement ?? la semaine n est tout simplement n + 1 dollars. Le paiement se d??veloppe ?? une vitesse constante de 1 $ par semaine.
Cette image montre un exemple un peu plus compliqu?? d'une fonction exponentielle d??passements fonctions sous-exponentielles:
La ligne rouge repr??sente 50 x, similaire ?? l'option 2 dans l'exemple ci-dessus, sauf en hausse de 50 par semaine au lieu de 1. Sa valeur est plus grand que x se d??place 7. La ligne bleue repr??sente le polyn??me x 3. Polyn??mes poussent subexponentially, puisque l'exposant (trois dans ce cas) reste constante alors que la base (x) des changements. Cette fonction est plus grande que les deux autres lorsque x est compris entre environ 7 et 9. Ensuite, la fonction exponentielle x 2 (en vert) prend le relais et devient plus grande que les deux autres fonctions pour tout x sup??rieur ?? environ 10.
Tout ce qui pousse par le m??me pourcentage chaque ann??e (ou chaque mois, jour, heure, etc.) est en croissance exponentielle. Par exemple, si le nombre moyen de descendants de chaque individu (ou un couple) dans une population reste constante, le taux de croissance est proportionnel au nombre d'individus. Une telle croissance d??mographique exponentielle cro??t trois fois plus vite quand il ya six millions de personnes comme il le fait quand il ya deux millions. Les comptes bancaires avec ?? taux fixe int??r??t compos?? cro??tre de fa??on exponentielle condition qu'il n'y ait pas de d??p??ts, retraits ou les frais de service. Math??matiquement, le solde du compte bancaire d'un compte commen??ant par S dollars, gagner un r annuelle de taux d'int??r??t et laiss?? intact pour n ann??es peut ??tre calcul??e comme 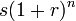 . Donc, dans un compte ?? partir de 1 $ et gagner 5% par an, le compte aura
. Donc, dans un compte ?? partir de 1 $ et gagner 5% par an, le compte aura 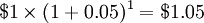 apr??s 1 an,
apr??s 1 an, 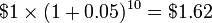 apr??s 10 ans, et $ 131,50 apr??s 100 ans. Depuis le solde de d??part et le taux ne changent pas, la quantit??
apr??s 10 ans, et $ 131,50 apr??s 100 ans. Depuis le solde de d??part et le taux ne changent pas, la quantit??  peut fonctionner comme la valeur k dans la formule k n donn?? plus t??t.
peut fonctionner comme la valeur k dans la formule k n donn?? plus t??t.
D??tails techniques
Soit x une quantit?? croissante de fa??on exponentielle par rapport au temps t. Par d??finition, le taux de variation dx / dt ob??it ?? l' ??quation diff??rentielle :
o?? k ≠ 0 est la constante de proportionnalit?? (par rapport au nombre moyen de descendants par individu dans le cas de la population). (Voir fonction logistique pour une simple correction de ce mod??le de croissance o?? k ne est pas constante). La solution de cette ??quation est la fonction exponentielle  - D'o?? le nom de croissance exponentielle (??e?? ??tant un constante math??matique). La constante
- D'o?? le nom de croissance exponentielle (??e?? ??tant un constante math??matique). La constante 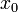 est la taille initiale de la population.
est la taille initiale de la population.
?? long terme, la croissance exponentielle de toute nature va d??passer la croissance lin??aire de toute nature (la base de la Catastrophe malthusienne) ainsi que tout polyn??me la croissance, ce est ?? dire, pour tout α:
Il ya toute une hi??rarchie des taux de croissance envisageables qui sont plus lents que exponentielle et plus rapide que lin??aire (?? long terme). Les taux de croissance peuvent ??galement ??tre plus rapide que exponentielle. Les mod??les lin??aires et exponentielles ne sont pas seulement les candidats simples mais sont celles de plus grande pr??sence dans la nature.
Dans l'??quation diff??rentielle ci-dessus, si k <0, alors les exp??riences de quantit?? d??croissance exponentielle.
Les quantit??s de caract??ristiques de croissance exponentielle
La loi de la croissance exponentielle peut ??tre ??crit dans des formes diff??rentes, mais math??matiquement ??quivalentes, en utilisant un autre socle . Les formes les plus communes sont les suivantes:
o??, comme dans l'exemple pr??c??dent x 0 exprime la quantit?? initiale (ce est ?? dire x (t) ?? t = 0).
La quantit?? k est appel?? la constante de croissance; la quantit?? r est appel?? le taux de croissance (pour cent d'augmentation par unit?? de temps); 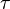 est le e temps de pliage; et T est la temps de doublement. Indiquant un de ces quatre quantit??s ??quivalentes permet de calculer automatiquement les trois autres, qui sont reli??s par l'??quation suivante (qui peut ??tre calcul?? en prenant le logarithme naturel de la ci-dessus):
est le e temps de pliage; et T est la temps de doublement. Indiquant un de ces quatre quantit??s ??quivalentes permet de calculer automatiquement les trois autres, qui sont reli??s par l'??quation suivante (qui peut ??tre calcul?? en prenant le logarithme naturel de la ci-dessus):
Une m??thode populaire approch??e de calcul du temps de doublement de la vitesse de croissance est la r??gle de 70, c.-??-  (Ou mieux:
(Ou mieux: 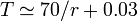 ).
).
Limitations de mod??les exponentiels
Un point important ?? propos de la croissance exponentielle est que, m??me quand il semble lent sur le court terme, il devient impressionnante rapide sur le long terme, avec la quantit?? initiale doubler au temps de doublement, puis doubler encore et encore. Par exemple, un taux de croissance de population de 2% par ann??e peut sembler petit, mais il implique effectivement doubler apr??s 35 ans, de doubler ?? nouveau apr??s encore 35 ans (ce est ?? dire devenir 4 fois la population initiale). Ceci implique que tant la quantit?? observ??e, et son d??riv?? de temps vont devenir de plusieurs ordres de grandeur plus grand que ce qui ??tait initialement entend par la personne qui a con??u le mod??le de croissance. Pour cette raison, certains effets pas initialement pris en compte seront fausser la loi de croissance, g??n??ralement mod??rer comme par exemple dans la loi logistique. La croissance exponentielle d'une quantit?? mise dans le monde r??el (c.-??-pas dans le monde abstrait des math??matiques) est un mod??le valable pour une p??riode temporaire seulement.
Pour cette raison, certaines personnes (voir par exemple Halte ?? la croissance) contestent le mod??le de croissance exponentielle sur le terrain qu'il est valide pour le court terme seulement, ce est ?? dire rien ne peut cro??tre ind??finiment. Par exemple, une population dans un environnement ferm?? ne peut pas continuer ?? cro??tre si elle mange toute la nourriture et les ressources disponibles; l'industrie ne peut pas continuer ?? pomper carbone de la clandestinit?? dans l'atmosph??re au-del?? des limites li??es ?? des r??servoirs de p??trole et les cons??quences de changement climatique . Les probl??mes de ce type existent pour chaque repr??sentation math??matique du monde r??el, mais sont sp??cialement sentir pendant la croissance exponentielle, puisque cette croissance mod??le acc??l??re comme variables augmentent dans un r??troaction positive, ?? un point o?? le temps de r??ponse humaine ?? inconv??nient peut ??tre insuffisante. Sur ces points, vous pouvez aussi les histoires exponentielles ci-dessous.
Des exemples de croissance exponentielle
- Biology .
- Les micro-organismes dans un bo??te de culture augmentera de mani??re exponentielle, au d??but, apr??s le premier micro-organisme semble (mais alors logistique jusqu'?? la nourriture disponible est ??puis??, lorsque la croissance se arr??te).
- Un virus ( SRAS, Du Nil occidental, la variole ) de l'infectiosit?? suffisante (k> 0) se propage de fa??on exponentielle au premier abord, si aucune artificielle immunisation est disponible. Chaque personne infect??e peut infecter plusieurs nouvelles personnes.
- La population humaine , si le nombre de naissances et de d??c??s par personne et par an devait rester aux niveaux actuels (mais aussi voir la croissance logistique).
- Beaucoup de r??ponses des ??tres vivants ?? stimuli, y compris l'homme perception, sont logarithmiques r??ponses, qui sont l'inverse de r??ponses exponentielles; la intensit?? et fr??quence de son sont per??us logarithmique, m??me avec tr??s faible stimulus, dans les limites de la perception. Ce est la raison pour laquelle la croissance exponentielle luminosit?? de stimuli visuels est per??u par l'??tre humain comme une augmentation lin??aire, plut??t que d'une augmentation exponentielle. Ceci a valeur de survie. En g??n??ral, il est important que les organismes ?? r??pondre ?? des stimuli dans une large gamme de niveaux, de tr??s faibles niveaux, ?? des niveaux tr??s ??lev??s, tandis que le la pr??cision de la estimation des diff??rences aux niveaux ??lev??s de relance est beaucoup moins important pour la survie.
- La technologie informatique
- La puissance de traitement des ordinateurs. Voir aussi la loi de Moore et singularit?? technologique (sous croissance exponentielle, il n'y a pas de singularit??s. La singularit?? est ici une m??taphore.).
- En th??orie de la complexit?? de calcul, des algorithmes informatiques de complexit?? exponentielle n??cessite une quantit?? exponentiellement croissante des ressources (temps, m??moire de l'ordinateur) pour seulement une augmentation constante de la taille du probl??me. Donc, pour un algorithme de complexit?? de temps 2 ^ x, si un probl??me de taille x = 10 n??cessite 10 secondes pour terminer, et un probl??me de taille x = 11 n??cessite 20 secondes, puis un probl??me de taille x = 12, il faudra 40 secondes. Ce type d'algorithme devient g??n??ralement inutilisable ?? tr??s petites tailles de probl??mes, souvent entre 30 et 100 ??l??ments (la plupart des algorithmes informatiques doivent ??tre en mesure de r??soudre des probl??mes beaucoup plus, jusqu'?? des dizaines de milliers, voire des millions d'articles dans des d??lais raisonnables, quelque chose qui serait ??tre physiquement impossible avec un algorithme exponentielle). En outre, les effets de la loi de Moore ne aident pas la situation beaucoup parce que doubler la vitesse du processeur permet simplement d'augmenter la taille du probl??me par une constante. Par exemple, si un processeur lent peut r??soudre les probl??mes de taille x au temps t, puis un processeur deux fois plus rapide ne pouvait r??soudre les probl??mes de taille x + constants dans le m??me temps t. Donc exponentielle des algorithmes complexes sont le plus souvent peu pratique, et la recherche d'algorithmes plus efficaces est l'un des objectifs centraux de la science informatique.
- la croissance du trafic Internet .
- Investissement. L'effet de l'int??r??t compos?? sur de nombreuses ann??es a un effet consid??rable sur l'??pargne et la capacit?? d'une personne ?? la retraite. Voir ??galement r??gle de 72
- Physique
- Dans un claquage par avalanche mat??riau di??lectrique. Un libre ??lectrons devient suffisamment acc??l??r?? par un appliqu?? de l'ext??rieur champ ??lectrique qu'il lib??re des ??lectrons suppl??mentaires qu'il entre en collision avec des atomes ou des mol??cules de la constante di??lectrique. Ces ??lectrons secondaires sont ??galement acc??l??r??es, la cr??ation d'un plus grand nombre d'??lectrons libres. La croissance exponentielle r??sultant des ??lectrons et des ions peut rapidement conduire ?? compl??ter la rupture di??lectrique du mat??riau.
- R??action nucl??aire en cha??ne (le concept derri??re armes nucl??aires ). Chaque uranium noyau qui subit une fission produit de multiples neutrons , dont chacun peut ??tre absorb?? par des atomes adjacents de l'uranium, les obligeant ?? fission ?? son tour. Si la probabilit?? d'absorption des neutrons sup??rieure ?? la probabilit?? de fuite de neutrons (une fonction de la forme et masse de l'uranium), k> 0 et donc le taux de neutrons de production et de fissions d'uranium induits augmente de fa??on exponentielle, dans une r??action incontr??l??e.
- Vente multiniveau
- Augmentations exponentielles sont promis ?? appara??tre dans chaque nouveau niveau de l'aval d'un ??l??ment de d??part que chaque membre ult??rieure recrute plus de gens.
Histoires exponentielles
Les caract??ristiques surprenantes de croissance exponentielle ont fascin?? les gens ?? travers les ??ges.
Riz sur un ??chiquier
Un courtisan pr??sent?? le roi de Perse avec une belle, fait-main ??chiquier. Le roi a demand?? ce qu'il aimerait en ??change de son don et le courtisan du roi surpris en demandant un grain de riz sur le premier carr??, deux grains sur la deuxi??me, quatre grains sur le troisi??me, etc. Le roi volontiers accept?? et demand?? le riz ?? apporter. Tout allait bien au d??but, mais l'exigence de  grains sur la
grains sur la  e carr?? exig?? plus d'un million de grains sur la 21e place, plus d'un quadrillion sur le 41e et il n'y avait tout simplement pas assez de riz dans le monde entier pour les places finales. (De Meadows et al. 1972, p.29 via Porritt 2005)
e carr?? exig?? plus d'un million de grains sur la 21e place, plus d'un quadrillion sur le 41e et il n'y avait tout simplement pas assez de riz dans le monde entier pour les places finales. (De Meadows et al. 1972, p.29 via Porritt 2005)
Pour voir variation de cette Seconde moiti?? de l'??chiquier en r??f??rence au point o?? un facteur croissance exponentielle commence ?? avoir un impact ??conomique significatif sur la strat??gie commerciale globale d'une organisation.
Le n??nuphar
Enfants fran??ais sont racont?? une histoire dans laquelle ils se imaginent avoir un ??tang avec n??nuphar feuilles flottant ?? la surface. La population lys double de taille tous les jours et si rien ne ??touffera l'??tang dans 30 jours, tuant tous les autres ??tres vivants dans l'eau. Jour apr??s jour, la plante semble petit et si il est d??cid?? de laisser cro??tre jusqu'?? ce qu'elle couvre la moiti?? de l'??tang, avant de le couper en arri??re. Ils sont ensuite invit??s, sur ce jour qui se produira. Ceci est r??v??l?? ??tre le 29e jour, puis il y aura une seule journ??e pour sauver l'??tang. (De Meadows et al. 1972, p.29 via Porritt 2005)