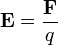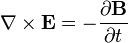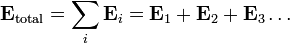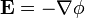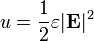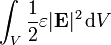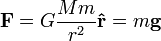Champ ??lectrique

Sujets connexes: l'??lectricit?? et de l'??lectronique

Contexte des ??coles Wikip??dia

Enfants SOS offrent un chargement complet de la s??lection pour les ??coles pour une utilisation sur les intranets des ??coles. Un lien rapide pour le parrainage d'enfants est http://www.sponsor-a-child.org.uk/

Electromagn??tisme

??lectricit?? Magn??tisme
??lectrostatique Charge ??lectrique ??lectricit?? statique Champ ??lectrique Conducteur Isolant Tribo??lectricit?? D??charge ??lectrostatique Induction La loi de Coulomb La loi de Gauss Flux ??lectrique / ??nergie potentielle Moment dipolaire ??lectrique Polarisation
Magn??tostatique La loi d'Amp??re Champ magn??tique Magn??tisation Flux magn??tique Loi de Biot-Savart Moment de dip??le magn??tique La loi de Gauss ?? magn??tisme
??lectrodynamique Droit de la force de Lorentz Induction ??lectromagn??tique La loi de Faraday La loi de Lenz D??placement actuel Les ??quations de Maxwell Champ ??lectromagn??tique Un rayonnement ??lectromagn??tique Tenseur de Maxwell Vecteur de Poynting Potentiel Li??nard-Wiechert Les ??quations de Jefimenko ?? courant de Foucault
R??seau ??lectrique Courant ??lectrique Potentiel ??lectrique Tension R??sistance La loi d'Ohm circuit de la s??rie Circuit parall??le Courant continu Courant alternatif Force ??lectromotrice Capacitance Inductance Imp??dance Cavit??s r??sonnantes Guides d'ondes
Formulation covariante Tenseur ??lectromagn??tique ( tenseur-??nergie) Four ?? courant continu Potentiel ??lectromagn??tique ?? quatre
Les scientifiques Amp??re Coulomb Faraday Gauss Heaviside Henri Hertz Lorentz Maxwell Tesla Volta Weber ??rsted

Dans la physique , l'espace entourant une charge ??lectrique ou en pr??sence d'un temps variant champ magn??tique poss??de une propri??t?? appel??e un champ ??lectrique. Ce champ ??lectrique exerce une force de sur d'autres objets charg??s ??lectriquement. Le concept d'un champ ??lectrique a ??t?? introduit par Michael Faraday .

Le champ ??lectrique est un champ de vecteur avec Unit??s SI newtons par Coulomb (NC ^-1) ou, de fa??on ??quivalente, volts par m??tre (V ^m-1). Les unit??s de base du champ ??lectrique sont kg ?? m ^-3 ?? s ?? A ^-1. L'intensit?? du champ en un point donn?? est d??finie comme la force qui serait exerc??e sur un positif charge de 1 coulomb plac?? ?? ce point de test; la direction du champ est donn??e par la direction de cette force. Les champs ??lectriques contiennent l'??nergie ??lectrique avec densit?? proportionnelle au carr?? de l'intensit?? du champ d'??nergie. Le champ ??lectrique est ?? se charger gravitationnelle acc??l??ration est ?? la masse et densit?? de force est de volume.

Une charge en mouvement a non seulement un champ ??lectrique mais aussi une champ magn??tique et, en g??n??ral, les champs ??lectriques et magn??tiques ne sont pas compl??tement ph??nom??nes distincts; ce qu'un observateur per??oit comme un champ ??lectrique, un autre observateur dans un autre cadre de r??f??rence per??oit comme un m??lange de champs ??lectriques et magn??tiques. Pour cette raison, on parle de " ??lectromagn??tisme "ou" champs ??lectromagn??tiques ". Dans la m??canique quantique , les perturbations dans les champs ??lectromagn??tiques sont appel??s photons , et l'??nergie des photons est quantifi??e.

D??finition

Un stationnaire charg??e particule dans un champ ??lectrique subit une vigueur proportionnelle ?? sa charge donn??e par l'??quation

$\ Mathbf {F} = q \ left [- \ nabla \ phi - \ frac {\ partial \ mathbf {A}} {\ t partielle} \ right]$

o?? la densit?? de flux magn??tique est donn??e par

$\ Mathbf {B} = \ nabla \ times \ mathbf {A}$

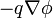et o?? $-q \ nabla \ phi$ est la force de Coulomb. (Voir la section ci-dessous).

La charge ??lectrique est une caract??ristique de certains particules subatomiques, et est quantifi??e lorsqu'elle est exprim??e comme un multiple de la dite charge ??l??mentaire $e$ . Les ??lectrons par convention ont une charge de -1, tandis que les protons ont une charge oppos??e de 1. Quarks avoir une charge fractionnaire de -1/3 +2/3 ou. Les ??quivalents de ces antiparticules ont une charge oppos??e. D'autres particules subatomiques porter de charge ??lectrique, comme muons et tauons.

En g??n??ral, de m??me signe se repoussent les particules charg??es un de l'autre, bien que diff??rente signe particules charg??es attirent. Ceci est exprim?? quantitativement dans la loi de Coulomb , qui stipule l'ampleur de la force de r??pulsion est proportionnelle au produit des deux accusations, et affaiblit proportionnellement au carr?? de la distance.

La charge ??lectrique d'un objet macroscopique est la somme des charges ??lectriques de ses particules constitutives. Souvent, la charge ??lectrique nette est ??gale ?? z??ro, ??tant donn?? que naturellement le nombre d'??lectrons dans chaque atome est ??gal au nombre de protons, de sorte que leurs charges se annulent. Les situations dans lesquelles la charge nette est non nul sont souvent appel??s ?? l'??lectricit?? statique. En outre, m??me lorsque la charge nette est nulle, il peut ??tre distribu?? de fa??on non uniforme (par exemple, en raison d'un champ ??lectrique externe), et ensuite le mat??riau est dit ??tre polaris??e, et la charge li??e ?? la polarisation est connu comme charges li??es (alors que l'exc??s de charge provenant de l'ext??rieur est appel?? charge libre). Un mouvement ordonn?? de particules charg??es dans une direction particuli??re (dans les m??taux, ce sont les ??lectrons) est connu comme courant ??lectrique. La nature discr??te de charge ??lectrique a ??t?? propos??e par Michael Faraday dans ses exp??riences d'??lectrolyse, alors directement d??montr??e par Robert Millikan dans son exp??rience oil-drop.

L'unit?? SI de la quantit?? d'??lectricit?? ou de charge ??lectrique est le coulomb, ce qui repr??sente environ 6,25 ?? 10 ¹⁸ charges ??l??mentaires (la charge sur un seul ??lectron ou un proton). Le coulomb est d??finie comme la quantit?? de charge qui a travers?? la section transversale d'un conducteur ??lectrique transportant un amp??re en une seconde. Le symbole 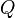$Q$ est souvent utilis?? pour d??signer une quantit?? d'??lectricit?? ou de frais. La quantit?? de charge ??lectrique peut ??tre mesur??e directement avec un ??lectrom??tre, ou indirectement mesur??e avec un galvanom??tre balistique.

Formellement, une mesure de la charge doit ??tre un multiple de la charge ??l??mentaire $e$ (Charge est quantifi??e), mais puisque ce est une moyenne, la quantit?? macroscopique, plusieurs ordres de grandeur sup??rieure ?? une charge ??l??mentaire seule, il peut effectivement prendre ne importe quelle valeur r??elle. En outre, dans certains contextes, il est utile de parler de fractions d'une charge; par exemple sous la charge d'un condensateur.

Si la particule charg??e peut ??tre consid??r?? comme un charge ponctuelle, le champ ??lectrique est d??finie comme la force qu'il subit par unit?? de charge:

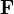$\ Mathbf {E} = \ frac {\ mathbf {F}} {q}$

o??

$\ Mathbf {F}$ est l'??lectrique vigueur v??cue par la particule

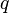$q$ est son accusation

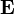$\ Mathbf {E}$ est le champ ??lectrique dans lequel se trouve la particule

Pris ?? la lettre, cette ??quation ne d??finit que le champ ??lectrique sur les lieux o?? il ya des frais fixes pr??sents en faire l'exp??rience. En outre, la force exerc??e par un autre responsable 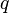$q$ va modifier la distribution de la source, ce qui signifie que le champ ??lectrique en pr??sence de 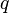$q$ diff??re de lui-m??me en l'absence de 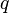$q$ . Cependant, le champ ??lectrique d'une distribution de source donn??e reste d??fini en l'absence de toute charge avec lequel interagir. Ceci est obtenu en mesurant la force exerc??e sur successivement plus petits charges d'essai plac??s au voisinage de la distribution source. Par ce processus, le champ ??lectrique cr???? par une distribution de source donn??e est d??fini comme la limite que la charge d'essai se rapproche de z??ro de la force par unit?? de charge exerc??e alors.

$\ Mathbf {E} = \ {lim_ q \ 0} \ frac {\ mathbf {F}} {q}$

Cela permet au champ ??lectrique d'??tre d??pendant de la distribution de source seul.

Ainsi qu'il ressort de la d??finition, la direction du champ ??lectrique est la m??me que la direction de la force qu'il exerce sur une particule charg??e positivement, et oppos??e ?? la direction de la force sur une particule charg??e n??gativement. Depuis charges identiques se repoussent et les contraires se attirent (telle que quantifi??e ci-dessous), le champ ??lectrique tend ?? pointer loin de charges positives et vers charges n??gatives.

La loi de Coulomb

Le champ ??lectrique entourant une charge ponctuelle est donn??e par la loi de Coulomb :

$\ Mathbf {E} = \ frac {1} {4 \ pi \ varepsilon_0} \ frac {} {Q r ^ 2} \ mathbf {\ hat {r}} \ qquad \ mbox {(1)}$

o??

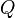$Q$ est la charge de la particule la cr??ation de la force ??lectrique,

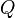$r$ est la distance de la particule de charge $Q$ au point d'??valuation de champ E,

$\ Mathbf {\ hat {r}}$ est le vecteur unitaire pointant de la particule de charge Q au point d'??valuation E-champ,

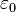$\ Varepsilon_0$ est le constante ??lectrique.

La loi de Coulomb est en fait un cas particulier de la loi de Gauss , une description plus fondamentale de la relation entre la r??partition de la charge ??lectrique dans l'espace et le champ ??lectrique r??sultant. La loi de Gauss est l'une des ??quations de Maxwell , un ensemble de quatre lois qui r??gissent l'??lectromagn??tisme.

champs variables dans le temps

Les charges ne produit pas seulement des champs ??lectriques. Comme ils se d??placent, ils g??n??rent des champs magn??tiques, et si le champ magn??tique change, il g??n??re des champs ??lectriques. Un changement champ magn??tique donne lieu ?? un champ ??lectrique,

$\ Mathbf {E} = - \ nabla \ phi - \ frac {\ partial \ mathbf {A}} {\ partial t}$

dont les rendements La loi de Faraday de l'induction,

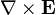$\ Nabla \ times \ mathbf {E} = - \ frac {\ partial \ mathbf {B}} {\ partial t}$

o??

$\ Nabla \ times \ mathbf {E}$ indique la courbure du champ ??lectrique,

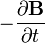$- \ Frac {\ partial \ mathbf {B}} {\ partial t}$ repr??sente la vitesse de diminution de vecteur champ magn??tique avec le temps.

Cela signifie qu'un champ magn??tique changeant dans le temps produit un champ ??lectrique boucl??e, peut-??tre aussi changer dans le temps. La situation dans laquelle les champs ??lectriques ou magn??tiques changent dans le temps ne est plus ??lectrostatique, mais plut??t ??lectrodynamique ou ??lectromagn??tique .

Propri??t??s (en ??lectrostatique)

Illustration du champ ??lectrique entourant un positive (rouge) et un (vert) charge n??gative.

Selon l'??quation (1) ci-dessus, le champ ??lectrique est fonction de la position. Le champ ??lectrique d?? ?? une seule charge tombe comme le carr?? de la distance de cette accusation.

Les champs ??lectriques suivent la principe de superposition. Si plus d'une accusation est pr??sent, le champ ??lectrique totale en tout point est ??gale ?? la somme vectorielle des champs ??lectriques respectifs que chaque objet serait de cr??er en l'absence des autres.

$\ Mathbf {e} _ {\ rm total} = \ sum_i \ mathbf {e} _i = \ mathbf {e} _1 + \ mathbf {e} _2 + \ mathbf {e} _3 \ ldots \, \!$

Si ce principe est ??tendu ?? un nombre infini de infiniment petits ??l??ments de la charge, les r??sultats de la formule suivante:

$\ Mathbf {E} = \ frac {1} {4 \ pi \ varepsilon_0} \ int \ frac {\ rho} {r ^ 2} \ mathbf {\ hat {r}} \, \ mathrm {d} V$

o??

$\ Rho$ est le la densit?? de charge, ou la quantit?? de charge par unit?? de volume .

Le champ ??lectrique en un point est ??gale ?? la n??gative du gradient potentiel ??lectrique bas. En symboles,

$\ Mathbf {E} = - \ nabla \ phi$

o??

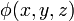$\ Phi (x, y, z)$ est le champ scalaire repr??sentant le potentiel ??lectrique en un point donn??.

Si plusieurs charges r??parties dans l'espace g??n??rent une telle potentiel ??lectrique, par exemple dans un solide , une gradient de champ ??lectrique peut ??galement ??tre d??fini.

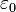Compte tenu de la permittivit?? $\ Varepsilon$ d'un mat??riau, qui peut ??tre diff??rente de la permittivit?? de l'espace libre $\ Varepsilon_ {0}$ , Le Induction ??lectrique est:

$\ Mathbf {D} = \ varepsilon \ mathbf {E}$

Dans le domaine de l'??nergie ??lectrique

Le champ ??lectrique stocke l'??nergie. La densit?? d'??nergie du champ ??lectrique est donn??e par

$u = \ frac {1} {2} \ varepsilon | \ mathbf {E} | ^ 2$

o??

$\ Varepsilon$ est le permittivit?? du milieu dans lequel le champ existe

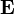$\ Mathbf {E}$ est le vecteur de champ ??lectrique.

L'??nergie totale stock??e dans le champ ??lectrique dans un volume V est donc donn??

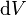$\ Int_ {V} \ frac {1} {2} \ varepsilon | \ mathbf {E} | ^ 2 \, \ mathrm {d} V$

o??

$\ Mathrm {d} V$ est l'??l??ment de volume diff??rentiel.

Parallels entre ??lectrostatique et gravit??

La loi de Coulomb , qui d??crit l'interaction des charges ??lectriques:

$\ Mathbf {F} = \ frac {1} {4 \ pi \ varepsilon_0} \ frac {} {Qq r ^ 2} \ mathbf {\ hat {r}} = q \ mathbf {E}$

est similaire ?? La loi de Newton de la gravitation universelle:

$\ Mathbf {F} = G \ frac {} {Mm r ^ 2} \ mathbf {\ hat {r}} = m \ mathbf {g}$

Ceci sugg??re similitudes entre le champ ??lectrique 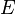$E$ et le champ de gravitation 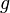$g$ , Donc parfois de masse est appel?? ??charge gravitationnelle".

Similitudes entre les forces ??lectrostatiques et gravitationnelles:

Agir ?? la fois dans le vide.
Les deux sont central et conservatrice.
Les deux ob??ir ?? un loi de l'inverse carr?? (les deux sont inversement proportionnelle ?? carr?? de r).
Les deux se propager ?? une vitesse finie c.

Diff??rences entre les forces ??lectrostatiques et gravitationnelles:

Des forces ??lectrostatiques sont beaucoup plus grandes que les forces de gravitation (d'environ 10 ³⁶ fois).
Les forces gravitationnelles sont attrayants pour les frais comme, alors que les forces ??lectrostatiques sont r??pulsive pour les frais similaires.
Il n'y a pas de charges gravitationnelles n??gatifs (pas masse n??gative) alors qu'il ya deux charges ??lectriques positives et n??gatives. Cette diff??rence combin??e avec pr??c??dente implique que les forces gravitationnelles sont toujours attrayante, tandis que les forces ??lectrostatiques peuvent ??tre soit attractive ou r??pulsive.
La charge ??lectrique est alors invariant masse relativiste ne est pas.

R??cup??r?? ?? partir de " http://en.wikipedia.org/w/index.php?title=Electric_field&oldid=316608188 "