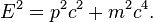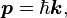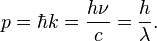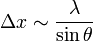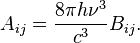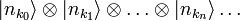Photon
Contexte des ??coles Wikip??dia
Ce contenu de Wikipedia a ??t?? s??lectionn?? par SOS Enfants d'aptitude dans les ??coles ?? travers le monde. M??res SOS chaque regard apr??s une une famille d'enfants parrain??s .
 Les photons ??mis dans un faisceau coh??rent ?? partir d'un laser | |
| Composition | Particule ??l??mentaire |
|---|---|
| Statistiques | Bosonique |
| Interactions | ??lectromagn??tique |
| Symbole | γ, h ν, ou ?? ω |
| Th??oris?? | Albert Einstein |
| Masse | 0 <1 ?? 10 -18 eV / c 2 |
| Dur??e de vie moyenne | Stable |
| Charge ??lectrique | 0 <1 ?? 10 -35 e |
| Tourner | 1 |
| Parit?? | -1 |
| C parit?? | -1 |
| Condens??e | Je ( J P C) = 0,1 (1 -) |
Un photon est un particule ??l??mentaire, le quantique de la lumi??re et toutes les autres formes de rayonnement ??lectromagn??tique , et forcer le support de force ??lectromagn??tique , m??me lorsque statique via photons virtuels. Les effets de cette vigueur sont facilement observables ?? la fois au et microscopique niveau macroscopique, parce que le photon n'a pas de masse au repos; ce qui permet de interactions ?? longue distance. Comme toutes les particules ??l??mentaires, les photons sont actuellement le mieux expliqu??es par la m??canique quantique et exposition dualit?? onde-particule, pr??sentant des propri??t??s de deux vagues et particules. Par exemple, un seul photon peut ??tre r??fract?? par une lentille ou une exposition agiter interf??rence avec lui-m??me, mais aussi agir comme une particule qui donne un r??sultat pr??cis quand son position est mesur??e.
Le concept de photon moderne a ??t?? d??velopp?? progressivement par Albert Einstein pour expliquer les observations exp??rimentales qui ne correspondaient pas au classique mod??le ondulatoire de la lumi??re. En particulier, le mod??le de photon repr??sente la d??pendance en fr??quence de l'??nergie de la lumi??re, et explique la capacit?? de la mati??re et le rayonnement d'??tre en ??quilibre thermique. Il a ??galement repr??sent?? observations anormales, y compris les propri??t??s de rayonnement du corps noir, que d'autres physiciens, notamment Max Planck , avait cherch?? ?? expliquer en utilisant des mod??les semi-classiques, dans lequel la lumi??re est toujours d??crit par les ??quations de Maxwell , mais les objets mat??riels qui ??mettent et absorbent la lumi??re, faire en quantit??s d'??nergie qui sont quantifi??es (ce est ?? dire, ils changent l'??nergie que par certaines quantit??s discr??tes particuliers et ne peut pas changer l'??nergie de quelque mani??re arbitraire). Bien que ces mod??les semi-classiques ont contribu?? au d??veloppement de la m??canique quantique, de nombreuses autres exp??riences ?? partir de Diffusion Compton des photons uniques par ??lectrons, d'abord observ??s en 1923, valid?? l'hypoth??se d'Einstein que la lumi??re elle-m??me est quantifi??. En 1926, le chimiste Gilbert N. Lewis a invent?? le nom photons pour ces particules, et apr??s 1927, lorsque Arthur H. Compton a remport?? le prix Nobel pour ses ??tudes de diffusion, la plupart des scientifiques ont accept?? la validit?? qui quanta de lumi??re ont une existence ind??pendante, et le photon terme de Lewis pour quanta de lumi??re a ??t?? accept??e.
Dans le mod??le standard de la physique des particules , les photons sont d??crits comme une cons??quence n??cessaire des lois physiques ayant une certaine sym??trie en tout point l'espace-temps. Les propri??t??s intrins??ques de photons, comme la charge , de masse et rotation, sont d??termin??es par les propri??t??s de cette ??valuer sym??trie. Le concept de photon a conduit ?? des avanc??es capitales en physique exp??rimentale et th??orique, comme les lasers , Condensation de Bose-Einstein, la th??orie quantique des champs , et de la interpr??tation probabiliste de la m??canique quantique. Elle a ??t?? appliqu??e ?? photochimie, microscopie ?? haute r??solution, et des mesures de distances mol??culaires. R??cemment, les photons ont ??t?? ??tudi??s comme des ??l??ments d' ordinateurs quantiques et pour des applications sophistiqu??es communication optique tel que la cryptographie quantique.
Nomenclature
| Le mod??le standard de la physique des particules |
|---|
 Grand collisionneur de hadrons du tunnel CERN |
Fond Physique des particules Mod??le Standard Th??orie quantique des champs th??orie de jauge Brisure spontan??e de sym??trie M??canisme de Higgs |
Constituants Interaction ??lectrofaible Chromodynamique quantique Matrice CKM |
Limites Probl??me de CP forte Probl??me de la hi??rarchie oscillations de neutrinos Voir aussi: Physique au-del?? du Mod??le Standard |
Les scientifiques Rutherford ?? Thomson ?? Chadwick ?? Bose ?? Sudarshan ?? Koshiba ?? Davis, Jr. ?? Anderson ?? ?? Fermi Dirac ?? Feynman ?? Rubbia ?? Gell-Mann ?? Kendall ?? Taylor ?? Friedman ?? Powell ?? PW Anderson ?? Glashow ?? Meer ?? Cowan ?? Nambu ?? Chamberlain ?? Cabibbo ?? Schwartz ?? Perl ?? Majorana ?? Weinberg ?? Lee ?? Ward ?? Salam ?? Kobayashi ?? Maskawa ?? Yang ?? Yukawa ?? 'T Hooft ?? Veltman ?? ?? Brut Politzer ?? Wilczek ?? Cronin ?? Fitch ?? Vleck ?? Higgs ?? Englert ?? Brout ?? Hagen ?? Guralnik ?? Kibble ?? Ting ?? Richter |
En 1900, Max Planck ??tait de travailler sur le rayonnement du corps noir et a sugg??r?? que l'??nergie des ondes ??lectromagn??tiques ne pouvait ??tre lib??r?? en "paquets" de l'??nergie. Dans son article de 1901 Annalen der Physik il a appel?? ces paquets "??l??ments de l'??nergie". Le mot quanta (du quantique singulier) a ??t?? utilis?? avant m??me 1900 pour d??signer des particules ou des quantit??s de diff??rentes quantit??s , y compris l'??lectricit?? . Plus tard, en 1905 Albert Einstein est all?? plus loin en sugg??rant que les ondes ??lectromagn??tiques ne peuvent exister que dans ces paquets d'ondes discr??tes. Il a appel?? une telle vague -packet les light quantum (allemand: das Lichtquant). Le nom photon provient du mot grec pour la lumi??re, φῶς (de Phos translitt??r??es), et a ??t?? invent?? en 1926 par le chimiste physique Gilbert Lewis, qui a publi?? une th??orie sp??culative dans laquelle les photons ??taient "incr??able et indestructible". Bien que la th??orie de Lewis n'a jamais ??t?? accept?? tel qu'il a ??t?? contredite par de nombreuses exp??riences, son nouveau nom, photon, a ??t?? imm??diatement adopt??e par la plupart des physiciens. Isaac Asimov cr??dits Arthur Compton de d??finir quanta d'??nergie sous forme de photons en 1923.
En physique, un photon est g??n??ralement d??sign?? par le symbole γ (la lettre grecque de gamma). Ce symbole pour le photon vient probablement du les rayons gamma, qui ont ??t?? d??couverts en 1900 par Paul Villard, nomm?? par Ernest Rutherford en 1903, et se est r??v??l?? ??tre une forme de rayonnement ??lectromagn??tique en 1914 par Rutherford et Edward Andrade. En chimie et ing??nierie optique, les photons sont g??n??ralement symbolis??s par hv, l'??nergie d'un photon, o?? h est Constante et la de Planck lettre grecque ν ( nu) est le photon de fr??quence. Beaucoup moins souvent, le photon peut ??tre symbolis?? par hf, o?? sa fr??quence est d??sign??e par f.
Propri??t??s physiques
Le photon est sans masse, n'a pas de charge ??lectrique , et est stable. Un photon a deux possible ??tats de polarisation et est d??crite par exactement trois param??tres continus: les composantes de son vecteur d'onde, qui d??terminent sa longueur d'onde λ et son sens de propagation. Le photon est le boson de jauge pour l'??lectromagn??tisme , et donc tous les autres nombres quantiques du photon (comme Num??ro lepton, nombre baryonique, et num??ros saveur quantique) sont nuls.
Les photons sont ??mis dans de nombreux processus naturels. Par exemple, quand une charge est acc??l??r??e il ??met rayonnement synchrotron. Au cours d'une mol??culaire , atomique ou nucl??aire transition inf??rieure ?? un niveau d'??nergie, les photons de diff??rentes ??nergie sera ??mis, ?? partir de la lumi??re infrarouge pour les rayons gamma. Un photon peut ??galement ??tre ??mis lorsque une particule et son correspondant antiparticule sont annihil?? (par exemple, annihilation ??lectron-positron).
Dans l'espace vide, le photon se d??place ?? c (la vitesse de la lumi??re ) et de son ??nergie et l'??lan sont li??s par E = pc, o?? p est le ampleur de la dynamique vecteur p. Cela d??coule de la relation relativiste suivante, avec m = 0:
L'??nergie et l'??lan d'un photon ne d??pendent que de son fr??quence (ν) ou inversement, la longueur d'onde (λ):
o?? k est le vecteur d'onde (o?? le nombre d'onde k = | k | = 2π / λ), ω = 2π ν est le fr??quence angulaire, et H = h / 2π est la r??duction constante de Planck.
Puisque p points dans la direction de la propagation du photon, l'amplitude de l'impulsion est
Le photon porte ??galement tourner moment angulaire qui ne d??pend pas de sa fr??quence. L'ampleur de son spin est 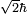 et la composante mesur??e le long de sa direction de mouvement, son h??licit??, doit ??tre de ?? h. Ces deux h??licit??s possibles, appel??s droitier et gaucher, correspondent aux deux possible des ??tats de polarisation circulaires du photon.
et la composante mesur??e le long de sa direction de mouvement, son h??licit??, doit ??tre de ?? h. Ces deux h??licit??s possibles, appel??s droitier et gaucher, correspondent aux deux possible des ??tats de polarisation circulaires du photon.
Pour illustrer l'importance de ces formules, l'an??antissement d'une particule ?? son antiparticule dans l'espace libre doit aboutir ?? la cr??ation d'au moins deux photons pour la raison suivante. Dans le centre de masse cadre, les antiparticules collision ne ont pas impulsion nette, alors qu'un seul photon a toujours dynamique (car il est d??termin??, comme nous l'avons vu, que par la fr??quence ou de la longueur d'onde des photons, qui ne peut pas ??tre z??ro). Par cons??quent, la conservation du moment (ou de mani??re ??quivalente, invariance translationnelle) exige qu'au moins deux photons sont cr????s, avec z??ro impulsion nette. (Toutefois, il est possible que si le syst??me interagit avec une autre particule ou d'un champ pour annihilation pour produire un photon, comme quand un positron annihile avec un ??lectron atomique li??, il est possible pour un seul photon d'??tre ??mis, que les pauses nucl??aires de champ de Coulomb sym??trie de translation.) L'??nergie des photons deux, ou, de fa??on ??quivalente, la fr??quence, peut ??tre d??termin??e ?? partir de conservation de quatre ??lan. Vu d'une autre mani??re, le photon peut ??tre consid??r?? comme sa propre antiparticule. Le processus inverse, la production de paires, est le m??canisme dominant par laquelle les photons de haute ??nergie telles que rayons gamma perdent de l'??nergie en passant ?? travers la mati??re. Ce processus est l'inverse de ??l'an??antissement d'un photon" permis dans le champ ??lectrique d'un noyau atomique.
Les formules classiques pour l'??nergie et l'??lan du rayonnement ??lectromagn??tique peuvent ??tre r??-exprim?? en termes d'??v??nements de photons. Par exemple, le pression du rayonnement ??lectromagn??tique sur un objet issue de l'apport de photons dynamique par unit?? de temps et unit?? de surface ?? cet objet, puisque la pression est la force par unit?? de surface et la force est le changement de dynamique par unit?? de temps.
V??rifications exp??rimentales sur la masse du photon
Le photon est actuellement compris ??tre strictement sans masse, mais ce est une question exp??rimentale. Si le photon ne est pas une particule sans masse strictement, il ne serait pas se d??placer ?? la vitesse exacte de la lumi??re dans le vide, c. Sa vitesse serait inf??rieur et d??pendra de sa fr??quence. Relativit?? serait pas affect??e par cette; la vitesse dite de la lumi??re, c, ne serait alors pas la vitesse r??elle ?? laquelle se d??place la lumi??re, mais une constante de la nature qui est la vitesse maximale que tout objet pourrait th??oriquement atteindre dans l'espace-temps. Ainsi, il serait encore la vitesse d'ondulations espace-temps ( ondes gravitationnelles et gravitons), mais ce ne serait pas la vitesse de photons.
Un photon massif aurait d'autres effets ainsi. la loi de Coulomb serait modifi??e et le champ ??lectromagn??tique aurait un degr?? de libert?? physique suppl??mentaire. Ces effets produisent des sondes exp??rimentales les plus sensibles de la masse de photons de la d??pendance en fr??quence de la vitesse de la lumi??re. Si la loi de Coulomb ne est pas exactement valide, qui pourrait entra??ner la pr??sence d'un champ ??lectrique dans un conducteur creux lorsqu'il est soumis ?? un champ ??lectrique externe. Celui-ci permet donc de tester la loi de Coulomb ?? une tr??s grande pr??cision. Un r??sultat nul d'une telle exp??rience a fix?? une limite de 10 m ≲ -14 eV / c 2.
Sharper limites sup??rieures ont ??t?? obtenus dans des exp??riences destin??es ?? d??tecter les effets caus??s par le galactique potentiel vecteur. Bien que le potentiel vecteur galactique est tr??s grande parce que le galactique champ magn??tique existe sur des ??chelles de longueur tr??s longues, que le champ magn??tique est observable si le photon est sans masse. Dans le cas d'un photon massif, le terme de masse 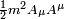 affecterait le plasma galactique. Le fait que de tels effets sont observ??s implique une limite sup??rieure de la masse de photons m <3 ?? 10 -27 eV / c 2. Le potentiel vecteur galactique peut ??galement ??tre sond?? directement en mesurant le couple exerc?? sur un anneau magn??tis??. Ces m??thodes ont ??t?? utilis??es pour obtenir la limite nette sup??rieure de 10 -18 eV / c 2 (l'??quivalent de 1,07 ?? 10 -27 unit??s de masse atomique) donn??e par Particle Data Group.
affecterait le plasma galactique. Le fait que de tels effets sont observ??s implique une limite sup??rieure de la masse de photons m <3 ?? 10 -27 eV / c 2. Le potentiel vecteur galactique peut ??galement ??tre sond?? directement en mesurant le couple exerc?? sur un anneau magn??tis??. Ces m??thodes ont ??t?? utilis??es pour obtenir la limite nette sup??rieure de 10 -18 eV / c 2 (l'??quivalent de 1,07 ?? 10 -27 unit??s de masse atomique) donn??e par Particle Data Group.
Ces limites nettes de la non-observation des effets provoqu??s par le potentiel vecteur galactique se sont r??v??l??s ??tre d??pendants mod??le. Si la masse de photons est g??n??r?? via la M??canisme de Higgs, puis la limite sup??rieure de m ≲10 -14 eV / c 2 de l'essai de la loi de Coulomb est valide.
Photons int??rieur supraconducteurs font d??velopper une non nulle masse au repos efficace; par cons??quent, des forces ??lectromagn??tiques ?? courte port??e deviennent supraconducteurs ?? l'int??rieur.
D??veloppement historique

Dans la plupart des th??ories jusqu'?? la dix-huiti??me si??cle, la lumi??re a ??t?? d??crite comme ??tant constitu??e de particules. Depuis mod??les de particules ne peuvent pas expliquer facilement pour le la r??fraction, diffraction et bir??fringence de la lumi??re, les th??ories ondulatoires de la lumi??re ont ??t?? propos??s par Ren?? Descartes (1637), Robert Hooke (1665), et Christian Huygens (1678); Cependant, les mod??les de particules rest??es dominante, principalement en raison de l'influence de Isaac Newton . Au d??but du XIXe si??cle, Thomas Young et Ao??t Fresnel a clairement d??montr?? la interf??rence et la diffraction de la lumi??re et en 1850 les mod??les de vagues ??taient g??n??ralement accept??es. En 1865, James Clerk Maxwell de pr??vision que la lumi??re ??tait une onde ??lectromagn??tique, qui a ??t?? confirm??e exp??rimentalement en 1888 par La d??tection de Heinrich Hertz des ondes radio -seemed ??tre le coup de gr??ce ?? des mod??les de particules de lumi??re.

Le Th??orie ondulatoire Maxwell, cependant, ne tient pas compte de toutes les propri??t??s de la lumi??re. La th??orie de Maxwell pr??dit que l'??nergie d'une onde lumineuse d??pend uniquement de sa intensit??, et non sur son fr??quence; N??anmoins, plusieurs types ind??pendantes de exp??riences montrent que l'??nergie communiqu??e par la lumi??re ?? des atomes ne d??pend que de la fr??quence de la lumi??re, et non sur son intensit??. Par exemple, certaines r??actions chimiques sont provoqu??es uniquement par une lumi??re de fr??quence sup??rieure ?? un certain seuil; lumi??re de fr??quence inf??rieure au seuil, ne importe comment intense, ne soit pas ?? la r??action. De m??me, les ??lectrons peuvent ??tre ??ject??s d'une plaque de m??tal en faisant la lumi??re de fr??quence suffisamment ??lev??e sur elle (la effet photo??lectrique); l'??nergie de l'??lectron ??ject?? est li??e uniquement ?? la fr??quence de la lumi??re, et non son intensit??.
Dans le m??me temps, les enqu??tes de rayonnement du corps noir r??alis??e sur quatre d??cennies (1860-1900) par divers chercheurs ont abouti ?? Max Planck de l ' hypoth??se que l'??nergie de ne importe quel syst??me qui absorbe ou ??met un rayonnement ??lectromagn??tique de fr??quence ν est un multiple entier d'un quantum d'??nergie E = hv. Comme le montre par Albert Einstein , une certaine forme de quantification de l'??nergie doit ??tre assum??e pour tenir compte de l'??quilibre thermique observ??e entre mati??re et rayonnement ??lectromagn??tique ; pour cette explication du effet photo??lectrique, Einstein a re??u le 1921 Prix Nobel de physique.
Comme la th??orie de Maxwell lumi??re permet de toutes les ??nergies possibles d'un rayonnement ??lectromagn??tique, la plupart des physiciens suppos?? initialement que la quantification de l'??nergie a entra??n?? une contrainte de inconnu sur la mati??re qui absorbe ou ??met le rayonnement. En 1905, Einstein a ??t?? le premier ?? proposer que la quantification de l'??nergie ??tait une propri??t?? de rayonnement ??lectromagn??tique lui-m??me. Bien qu'il ait accept?? la validit?? de la th??orie de Maxwell, Einstein a fait remarquer que de nombreuses exp??riences anormales pourraient se expliquer si l'??nergie d'une onde lumineuse de Maxwell ont ??t?? localis??s dans le point comme quanta qui se d??placent ind??pendamment l'un de l'autre, m??me si la vague elle-m??me se ??tend en continu sur espace. En 1909 et 1916, Einstein a montr?? que, si La loi de Planck du rayonnement du corps noir est accept??e, le quanta d'??nergie doit ??galement effectuer dynamique p = h / λ, ce qui les rend ?? part enti??re particules. Cet ??lan de photons a ??t?? observ?? exp??rimentalement par Arthur Compton, pour lequel il a re??u le Prix Nobel en 1927. La question centrale est alors: comment unifier la th??orie ondulatoire de la lumi??re de Maxwell avec sa nature de particules observ??es exp??rimentalement? La r??ponse ?? cette question a occup?? Albert Einstein pour le reste de sa vie, et a ??t?? r??solu ??lectrodynamique quantique et son successeur, le mod??le standard (voir seconde quantification et Le photon comme un boson de jauge , ci-dessous).
Les premi??res objections

1905 pr??dictions d'Einstein ont ??t?? v??rifi??es exp??rimentalement de plusieurs fa??ons dans les deux premi??res d??cennies du 20e si??cle, comme l'a racont?? dans La conf??rence Nobel de Robert Millikan. Toutefois, avant de L'exp??rience de Compton montrant que les photons r??alis??es impulsion proportionnelle ?? leur nombre d'onde (ou fr??quence) (1922), la plupart des physiciens ??taient r??ticents ?? croire que le rayonnement ??lectromagn??tique lui-m??me pourrait ??tre particulaire. (Voir, par exemple, les conf??rences de Nobel Wien, Planck et Millikan.). Au lieu de cela, il y avait une croyance largement r??pandue que la quantification de l'??nergie r??sulte d'une contrainte inconnu sur la mati??re qui absorbe ou ??met un rayonnement. Les attitudes ont chang?? au fil du temps. En partie, le changement peut ??tre attribu??e ?? des exp??riences telles que Diffusion Compton, o?? il ??tait beaucoup plus difficile de ne pas attribuer la quantification se allume pour expliquer les r??sultats observ??s.
M??me apr??s l'exp??rience de Compton, Niels Bohr , Hendrik Kramers et John Slater a fait une derni??re tentative pour pr??server le mod??le continue de champ ??lectromagn??tique de Maxwell de la lumi??re, le soi-disant BKS mod??le. Pour tenir compte des donn??es alors disponibles, deux hypoth??ses drastiques devaient ??tre prises:
- L'??nergie et l'??lan sont conserv??es uniquement sur la moyenne dans les interactions entre mati??re et rayonnement, pas dans les processus ??l??mentaires tels que l'absorption et d'??mission. Cela permet de concilier l'??nergie discontinue ??volution de l'atome (saut entre les Etats de l'??nergie) avec la lib??ration continue d'??nergie en rayonnement.
- La causalit?? est abandonn??. Par exemple, ne sont que des ??missions spontan??es ??missions induites par un champ ??lectromagn??tique ??virtuel??.
Cependant, les exp??riences ont montr?? que Compton raffin??s impulsion-??nergie est conserv??e extraordinairement bien dans les processus ??l??mentaires; et aussi que les cahots de l'??lectron et la g??n??ration d'un nouveau photon dans Diffusion Compton ob??ir causalit?? dans les 10 ps. En cons??quence, Bohr et ses coll??gues ont donn?? leur mod??le ??comme un enterrement honorable que possible". N??anmoins, les ??checs du mod??le BKS inspir??s Werner Heisenberg dans son d??veloppement de m??canique des matrices.
Quelques physiciens ont persist?? dans l'??laboration de mod??les semi-classiques dans lequel le rayonnement ??lectromagn??tique ne est pas quantifi??, mais appara??t mati??re d'ob??ir aux lois de la m??canique quantique . Bien que les preuves pour les photons d'exp??riences chimiques et physiques ??tait ??crasante par les ann??es 1970, cette preuve ne pouvait ??tre consid??r??e comme absolument d??finitif; car il se est appuy?? sur l'interaction de la lumi??re avec la mati??re, une th??orie suffisamment compliqu??e de la mati??re pourrait en principe compte les ??l??ments de preuve. N??anmoins, toutes les th??ories semi-classiques ont ??t?? r??fut??es d??finitivement dans les ann??es 1970 et 1980 par des exp??riences photons corr??lation. Par cons??quent, l'hypoth??se d'Einstein que la quantification est une propri??t?? de la lumi??re elle-m??me est consid??r?? ??tre prouv??e.
Principes de dualit?? et d'incertitude onde-particule
Photons, comme tous les objets quantiques, pr??sentent ?? la fois des propri??t??s ondulatoires et de particules ressemblant. Leur double nature onde-particule peut ??tre difficile ?? visualiser. Les ph??nom??nes photons affiche clairement comme une vague tels que diffraction et interf??rence sur l'??chelle de longueur de sa longueur d'onde. Par exemple, un photon unique passant ?? travers une terres de Fentes de Young sur l'??cran pr??sentant des ph??nom??nes d'interf??rence mais seulement si aucune mesure n'a ??t?? faite sur la fente r??elle ??tant traversent. Pour tenir compte de l'interpr??tation de particules ce ph??nom??ne est appel?? distribution de probabilit?? , mais se comporte selon les ??quations de Maxwell . Cependant, des exp??riences confirment que le photon ne est pas une courte impulsion de rayonnement ??lectromagn??tique; qu'il ne se propage pas comme il se propage, ni ne divise quand il rencontre un diviseur faisceau. Au contraire, le photon semble ??tre un ponctuelle particules car elle est absorb??e ou ??mise dans son ensemble par arbitrairement petits syst??mes, des syst??mes beaucoup plus petites que la longueur d'onde, comme un noyau atomique (≈10 -15 m de diam??tre) ou m??me le point-like ??lectrons . N??anmoins, le photon ne est pas une particule ponctuelle dont la trajectoire est en forme probabiliste par le champ ??lectromagn??tique, telle que con??ue par Einstein et d'autres; cette hypoth??se a ??galement ??t?? r??fut??e par les exp??riences de photons corr??lation cit??s ci-dessus. Selon nos connaissances actuelles, le champ ??lectromagn??tique se est produite par des photons, qui ?? son tour ?? partir d'un r??sultat locale ??valuer la sym??trie et les lois de la th??orie quantique des champs (voir la seconde quantification et Boson de jauge sections ci-dessous).

Un ??l??ment cl?? de la m??canique quantique est Heisenberg principe d'incertitude, qui interdit la mesure simultan??e de la position et la vitesse d'une particule dans la m??me direction. Remarquablement, le principe d'incertitude pour charg??es, particules mat??rielles n??cessite la quantification de la lumi??re en photons, et m??me la d??pendance en fr??quence de l'??nergie et de l'impulsion du photon. Une illustration ??l??gante est Heisenberg pens?? exp??rience pour localiser un ??lectron avec un microscope id??al. La position de l'??lectron peut ??tre d??termin??e ?? l'int??rieur de la puissance du microscope, qui est donn??e par la formule classique de la r??solution optique
o??  est le angle d'ouverture du microscope. Ainsi, l'incertitude de position
est le angle d'ouverture du microscope. Ainsi, l'incertitude de position 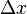 peut ??tre faite arbitrairement petit en r??duisant la longueur d'onde λ. La dynamique de l'??lectron est incertain, car il a re??u un "kick"
peut ??tre faite arbitrairement petit en r??duisant la longueur d'onde λ. La dynamique de l'??lectron est incertain, car il a re??u un "kick" 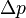 de la diffusion de la lumi??re de celle-ci dans le microscope. Si la lumi??re ne ont pas ??t?? quantifi?? en photons, l'incertitude
de la diffusion de la lumi??re de celle-ci dans le microscope. Si la lumi??re ne ont pas ??t?? quantifi?? en photons, l'incertitude 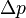 pourrait ??tre faite arbitrairement petit en r??duisant l'intensit?? de la lumi??re. Dans ce cas, puisque la longueur d'onde et l'intensit?? de la lumi??re peuvent ??tre modifi??es ind??pendamment, on pourrait d??terminer simultan??ment la position et l'impulsion arbitrairement grande pr??cision, violation de la principe d'incertitude. En revanche, la formule d'Einstein pour les photons dynamique pr??serve le principe d'incertitude; depuis le photon est dispers?? ne importe o?? dans l'ouverture, l'incertitude de l'??lan transf??r?? ??gaux
pourrait ??tre faite arbitrairement petit en r??duisant l'intensit?? de la lumi??re. Dans ce cas, puisque la longueur d'onde et l'intensit?? de la lumi??re peuvent ??tre modifi??es ind??pendamment, on pourrait d??terminer simultan??ment la position et l'impulsion arbitrairement grande pr??cision, violation de la principe d'incertitude. En revanche, la formule d'Einstein pour les photons dynamique pr??serve le principe d'incertitude; depuis le photon est dispers?? ne importe o?? dans l'ouverture, l'incertitude de l'??lan transf??r?? ??gaux
pour obtenir le produit  , Qui est le principe d'incertitude de Heisenberg. Ainsi, le monde entier est quantifi??; la mati??re et les champs doivent ob??issent ?? un ensemble coh??rent de lois quantiques, si l'un est ?? quantifier.
, Qui est le principe d'incertitude de Heisenberg. Ainsi, le monde entier est quantifi??; la mati??re et les champs doivent ob??issent ?? un ensemble coh??rent de lois quantiques, si l'un est ?? quantifier.
Le principe d'incertitude analogue pour les photons interdit la mesure simultan??e du nombre  de photons (voir ??tat de Fock et de la seconde quantification section ci-dessous) dans une onde ??lectromagn??tique et la phase
de photons (voir ??tat de Fock et de la seconde quantification section ci-dessous) dans une onde ??lectromagn??tique et la phase 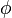 de cette vague
de cette vague
Voir ??tat coh??rent et press?? ??tat coh??rent pour plus de d??tails.
Les deux photons et de particules mat??rielles telles que des ??lectrons cr??ent analogue motifs d'interf??rence lors du passage ?? travers un Fentes de Young. Pour des photons, ce qui correspond ?? l'interf??rence d'une Onde lumineuse Maxwell alors que, pour les particules mat??rielles, ce qui correspond ?? l'interf??rence de la ??quation d'onde de Schr??dinger. Bien que cette similitude pourrait sugg??rer que les ??quations de Maxwell sont tout simplement l'??quation de Schr??dinger pour les photons, la plupart des physiciens ne se entendent pas. Pour une chose, ils sont math??matiquement diff??rents; de toute ??vidence, une ??quation de Schr??dinger r??sout un complexe champ, tandis que quatre ??quations de Maxwell pour r??soudre de v??ritables champs. Plus g??n??ralement, le concept normal d'un Schr??dinger probabilit?? fonction d'onde ne peut pas ??tre appliqu??e ?? des photons. ??tre sans masse, ils ne peuvent pas ??tre localis??s sans ??tre d??truite; techniquement, les photons ne peuvent pas avoir une position eigenstate  , Et, par cons??quent, le principe d'incertitude de Heisenberg normale
, Et, par cons??quent, le principe d'incertitude de Heisenberg normale 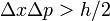 ne concernent pas les photons. Quelques fonctions d'onde de substitution ont ??t?? sugg??r??es pour le photon, mais ils ne sont pas venus dans l'usage g??n??ral. Au lieu de cela, les physiciens acceptent g??n??ralement le deuxi??me quantifi?? th??orie de photons d??crit ci-dessous, ??lectrodynamique quantique, dans laquelle les photons sont des excitations quantifi??es des modes ??lectromagn??tiques.
ne concernent pas les photons. Quelques fonctions d'onde de substitution ont ??t?? sugg??r??es pour le photon, mais ils ne sont pas venus dans l'usage g??n??ral. Au lieu de cela, les physiciens acceptent g??n??ralement le deuxi??me quantifi?? th??orie de photons d??crit ci-dessous, ??lectrodynamique quantique, dans laquelle les photons sont des excitations quantifi??es des modes ??lectromagn??tiques.
Mod??le de Bose-Einstein d'un gaz de photons
En 1924, Satyendra Nath Bose d??riv?? La loi de Planck du rayonnement du corps noir sans utiliser l'??lectromagn??tisme, mais plut??t une modification de comptage de gros grains de l'espace de phase. Einstein a montr?? que cette modification revient ?? supposer que les photons sont rigoureusement identiques et qu'il impliquait une "interaction non locale myst??rieuse", maintenant compris que l'exigence d'une ??tat m??canique quantique sym??trique. Ce travail a conduit ?? la notion de ??tats coh??rents et le d??veloppement du laser. Dans les m??mes documents, Einstein a prolong?? le formalisme de Bose ?? particules mat??rielles ( bosons) et pr??dit qu'ils se condenser dans leur ??tat le plus bas quantique ?? des temp??ratures suffisamment basses; cette Condensation de Bose-Einstein a ??t?? observ?? exp??rimentalement en 1995. Il a ensuite ??t?? utilis?? par Lene Hau ?? ralentir, puis arr??ter compl??tement, la lumi??re en 1999 et 2001.
La conception moderne ?? cela est que les photons sont, en raison de leur spin entier, bosons (par opposition ?? fermions de spin demi-entier). Par le Th??or??me spin-statistique, tous les bosons ob??issent statistique de Bose-Einstein (alors que tous les fermions ob??issent Fermi-Dirac statistiques).
Stimul?? et ??mission spontan??e

En 1916, Einstein a montr?? que la loi de rayonnement de Planck pourrait ??tre d??riv?? d'un traitement statistique semi-classique de photons et d'atomes, ce qui implique une relation entre les taux ?? laquelle les atomes ??mettent et absorbent les photons. La condition r??sulte de l'hypoth??se selon laquelle la lumi??re est ??mise et absorb??e par des atomes ind??pendamment, et que l'??quilibre thermique est conserv??e par interaction avec des atomes. Consid??rons une cavit?? dans l'??quilibre thermique et rempli avec un rayonnement ??lectromagn??tique et les atomes qui peuvent ??mettre et absorber ce rayonnement. ??quilibre thermique n??cessite que la densit?? d'??nergie  de photons de fr??quence
de photons de fr??quence 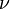 (Qui est proportionnelle ?? leur densit?? en nombre) est, en moyenne, constante dans le temps; par cons??quent, la vitesse ?? laquelle des photons d'une fr??quence donn??e sont ??mis doit ??tre ??gale ?? la vitesse de les absorber.
(Qui est proportionnelle ?? leur densit?? en nombre) est, en moyenne, constante dans le temps; par cons??quent, la vitesse ?? laquelle des photons d'une fr??quence donn??e sont ??mis doit ??tre ??gale ?? la vitesse de les absorber.
Einstein a commenc?? en postulant relations simples de proportionnalit?? pour les diff??rentes vitesses de r??action impliqu??s. Dans son mod??le, le taux 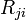 pour un syst??me d'absorber un photon de fr??quence
pour un syst??me d'absorber un photon de fr??quence 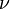 et passage d'une ??nergie plus faible
et passage d'une ??nergie plus faible  ?? une ??nergie plus ??lev??e
?? une ??nergie plus ??lev??e 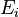 est proportionnelle au nombre
est proportionnelle au nombre 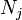 d'atomes avec l'??nergie
d'atomes avec l'??nergie  et ?? la densit?? d'??nergie
et ?? la densit?? d'??nergie  de photons ambiantes avec cette fr??quence,
de photons ambiantes avec cette fr??quence,
o??  est le taux constant pour l'absorption. Pour le processus inverse, il ya deux possibilit??s: l'??mission spontan??e d'un photon, et un retour ?? l'??tat inf??rieur d'??nergie qui est initi??e par l'interaction avec un photon de passage. Suite ?? l'approche d'Einstein, le taux correspondant
est le taux constant pour l'absorption. Pour le processus inverse, il ya deux possibilit??s: l'??mission spontan??e d'un photon, et un retour ?? l'??tat inf??rieur d'??nergie qui est initi??e par l'interaction avec un photon de passage. Suite ?? l'approche d'Einstein, le taux correspondant  pour l'??mission de photons de fr??quence
pour l'??mission de photons de fr??quence 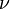 et passage d'une ??nergie plus ??lev??e
et passage d'une ??nergie plus ??lev??e 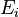 ?? une ??nergie plus faible
?? une ??nergie plus faible  est
est
o??  est la constante de vitesse de l'??mission d'un photon spontan??ment, et
est la constante de vitesse de l'??mission d'un photon spontan??ment, et  est la constante de vitesse pour ??mettre en r??ponse ?? des photons ambiantes ( ou induite par l'??mission stimul??e). Dans l'??quilibre thermodynamique, le nombre d'atomes dans l'??tat i et que d'atomes dans l'??tat j doivent, en moyenne, ??tre constante; Par cons??quent, les taux
est la constante de vitesse pour ??mettre en r??ponse ?? des photons ambiantes ( ou induite par l'??mission stimul??e). Dans l'??quilibre thermodynamique, le nombre d'atomes dans l'??tat i et que d'atomes dans l'??tat j doivent, en moyenne, ??tre constante; Par cons??quent, les taux 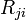 et
et  doit ??tre ??gal. En outre, par des arguments analogues ?? la d??rivation de Les statistiques de Boltzmann, le rapport de
doit ??tre ??gal. En outre, par des arguments analogues ?? la d??rivation de Les statistiques de Boltzmann, le rapport de  et
et 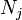 est
est 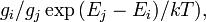 o??
o?? 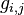 sont les la d??g??n??rescence de l'Etat et celle de i j, respectivement,
sont les la d??g??n??rescence de l'Etat et celle de i j, respectivement, 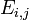 leurs ??nergies, k la La constante de Boltzmann et T est le syst??me temp??rature . De ce fait, il est ais??ment d??duire que
leurs ??nergies, k la La constante de Boltzmann et T est le syst??me temp??rature . De ce fait, il est ais??ment d??duire que 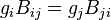 et
et
A et B sont collectivement connus comme les coefficients d'Einstein.
Einstein ne pouvait pas justifier pleinement ses ??quations de taux, mais affirm?? qu'il devrait ??tre possible de calculer les coefficients  ,
,  et
et  fois physiciens avaient obtenu "la m??canique et de l'??lectrodynamique modifi??s pour tenir compte de l'hypoth??se quantique". En fait, en 1926, Paul Dirac d??riv?? du
fois physiciens avaient obtenu "la m??canique et de l'??lectrodynamique modifi??s pour tenir compte de l'hypoth??se quantique". En fait, en 1926, Paul Dirac d??riv?? du  constantes de vitesse en utilisant une approche semi-classique, et, en 1927, ont r??ussi ?? tirer toutes les constantes de vitesse de premiers principes dans le cadre de la th??orie quantique. Le travail de Dirac ??tait le fondement de l'??lectrodynamique quantique, ?? savoir, la quantification de champ ??lectromagn??tique lui-m??me. L'approche de Dirac est aussi appel?? seconde quantification ou la th??orie quantique des champs ; traitements m??caniques quantiques ant??rieures ne traitent particules mat??rielles que m??canique, pas le champ ??lectromagn??tique quantique.
constantes de vitesse en utilisant une approche semi-classique, et, en 1927, ont r??ussi ?? tirer toutes les constantes de vitesse de premiers principes dans le cadre de la th??orie quantique. Le travail de Dirac ??tait le fondement de l'??lectrodynamique quantique, ?? savoir, la quantification de champ ??lectromagn??tique lui-m??me. L'approche de Dirac est aussi appel?? seconde quantification ou la th??orie quantique des champs ; traitements m??caniques quantiques ant??rieures ne traitent particules mat??rielles que m??canique, pas le champ ??lectromagn??tique quantique.
Einstein a ??t?? troubl?? par le fait que sa th??orie semblait incompl??te, car elle n'a pas d??termin?? la direction d'un photon ??mis spontan??ment. Une nature probabiliste du mouvement lumi??re particules a ??t?? consid??r??e par Newton dans son traitement de la bir??fringence et, plus g??n??ralement, de la s??paration de faisceaux lumineux au niveau des interfaces en un faisceau transmis et un faisceau r??fl??chi. Newton hypoth??se que variables cach??es dans la particule de lumi??re d??termin??es voie qu'il suivrait. De m??me, Einstein esp??rait une th??orie plus compl??te qui rien laisser au hasard, en commen??ant sa s??paration de la m??canique quantique. Ironiquement, Max Born de interpr??tation probabiliste de la fonction d'onde a ??t?? inspir?? par le travail d'Einstein tard la recherche d'une th??orie plus compl??te.
Deuxi??me quantification
En 1910, Peter Debye d??riv?? La loi de Planck du rayonnement du corps noir ?? partir d'une hypoth??se relativement simple. Il d??compos?? correctement le champ ??lectromagn??tique dans une cavit?? en son modes de Fourier, et suppose que l'??nergie dans ne importe quel mode est un multiple entier de 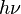 O??
O?? 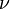 est la fr??quence du mode ??lectromagn??tique. La loi de Planck du rayonnement du corps noir suit imm??diatement comme une somme g??om??trique. Cependant, l'approche de Debye omis de donner la bonne formule pour les fluctuations d'??nergie de rayonnement du corps noir, qui ont ??t?? per??us par Einstein en 1909.
est la fr??quence du mode ??lectromagn??tique. La loi de Planck du rayonnement du corps noir suit imm??diatement comme une somme g??om??trique. Cependant, l'approche de Debye omis de donner la bonne formule pour les fluctuations d'??nergie de rayonnement du corps noir, qui ont ??t?? per??us par Einstein en 1909.
En 1925, N??, Heisenberg et Jordan r??interpr??t?? le concept de Debye dans un moyen cl??. Comme on peut le montre classique, le les modes de Fourier un champ ??lectromagn??tique ensemble complet d'ondes planes ??lectromagn??tiques index??s par leur vecteur d'onde k et de polarisation ??tat sont ??quivalentes ?? un ensemble de d??coupl?? oscillateurs harmoniques simples. Quantique trait??e m??caniquement, les niveaux de ces oscillateurs d'??nergie sont connus pour ??tre  O??
O?? 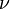 est la fr??quence de l'oscillateur. La nouvelle ??tape cl?? ??tait d'identifier un mode ??lectromagn??tique avec l'??nergie
est la fr??quence de l'oscillateur. La nouvelle ??tape cl?? ??tait d'identifier un mode ??lectromagn??tique avec l'??nergie  comme un ??tat avec
comme un ??tat avec  photons, chacun de l'??nergie
photons, chacun de l'??nergie 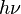 . Cette approche donne la formule de fluctuation d'??nergie correcte.
. Cette approche donne la formule de fluctuation d'??nergie correcte.

Dirac a pris un peu plus loin. Il a trait?? l'interaction entre un champ ??lectromagn??tique comme une petite perturbation qui induit des transitions dans les Etats de photons, en changeant le nombre de photons dans les modes de charge et, tout en conservant l'??nergie et l'??lan g??n??ral. Dirac a pu tirer Einstein  et
et  coefficients de premiers principes, et ont montr?? que les statistiques de Bose-Einstein de photons est une cons??quence naturelle de quantification du champ ??lectromagn??tique correctement (le raisonnement de Bose est all?? dans la direction oppos??e, il d??rive La loi de Planck du rayonnement du corps noir en supposant statistiques B-E). Au temps de Dirac, il ne ??tait pas encore connu que tous les bosons, y compris les photons, doivent ob??ir ?? la statistique de Bose-Einstein.
coefficients de premiers principes, et ont montr?? que les statistiques de Bose-Einstein de photons est une cons??quence naturelle de quantification du champ ??lectromagn??tique correctement (le raisonnement de Bose est all?? dans la direction oppos??e, il d??rive La loi de Planck du rayonnement du corps noir en supposant statistiques B-E). Au temps de Dirac, il ne ??tait pas encore connu que tous les bosons, y compris les photons, doivent ob??ir ?? la statistique de Bose-Einstein.
Second ordre de Dirac la théorie de la perturbation peut impliquer photons virtuels, états intermédiaires transitoires du champ électromagnétique; les statiques électriques et magnétiques interactions sont médiées par ces photons virtuels. Dans ces théories quantiques des champs , l' amplitude de probabilité des événements observables est calculée en additionnant toutes les étapes intermédiaires possibles, même celles qui sont non physique; par conséquent, les photons virtuels ne sont pas contraints de satisfaire  , et peuvent avoir supplémentaires états de polarisation; en fonction de la jauge utilisée, photons virtuels peuvent avoir trois ou quatre états de polarisation, au lieu des deux états de photons réels. Bien que ces photons virtuels transitoires ne peuvent jamais être observés, ils contribuent de façon mesurable les probabilités d'événements observables. En effet, comme de second ordre et les calculs de perturbation d'ordre supérieur peuvent donner apparemment infinies contributions à la somme. Ces résultats non physiques sont corrigées pour l'utilisation de la technique de renormalisation . D'autres particules virtuelles peuvent contribuer à la somme ainsi; par exemple, deux photons peuvent interagir indirectement par l'intermédiaire virtuel électronique - positron paires. En fait, cette diffusion photon-photon, ainsi que la diffusion électron-photon, qui est censé être l'un des modes d'exploitation de l'accélérateur de particules prévu, le collisionneur linéaire international.
, et peuvent avoir supplémentaires états de polarisation; en fonction de la jauge utilisée, photons virtuels peuvent avoir trois ou quatre états de polarisation, au lieu des deux états de photons réels. Bien que ces photons virtuels transitoires ne peuvent jamais être observés, ils contribuent de façon mesurable les probabilités d'événements observables. En effet, comme de second ordre et les calculs de perturbation d'ordre supérieur peuvent donner apparemment infinies contributions à la somme. Ces résultats non physiques sont corrigées pour l'utilisation de la technique de renormalisation . D'autres particules virtuelles peuvent contribuer à la somme ainsi; par exemple, deux photons peuvent interagir indirectement par l'intermédiaire virtuel électronique - positron paires. En fait, cette diffusion photon-photon, ainsi que la diffusion électron-photon, qui est censé être l'un des modes d'exploitation de l'accélérateur de particules prévu, le collisionneur linéaire international.
Dans la notation de la physique moderne, l'état ??????quantique du champ électromagnétique est écrit comme unétat ??????de Fock, unproduit des États tenseur pour chaque mode électromagnétique
o?? 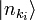 représente l'état dans lequel
représente l'état dans lequel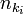 les photons sont dans le mode
les photons sont dans le mode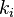 .Dans cette notation, la création d'un nouveau photon dans le mode
.Dans cette notation, la création d'un nouveau photon dans le mode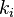 (par exemple, émis à partir d'une transition atomique) est écrit que
(par exemple, émis à partir d'une transition atomique) est écrit que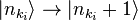 .cette notation exprime simplement le concept de Born, Heisenberg et la Jordanie décrits ci-dessus, et ne pas ajouter toute la physique.
.cette notation exprime simplement le concept de Born, Heisenberg et la Jordanie décrits ci-dessus, et ne pas ajouter toute la physique.
Les propriétés hadronique du photon
Les mesures de l'interaction entre photons énergétiques et hadrons montrent que l'interaction est beaucoup plus intense que prévu par l'interaction des photons avec seulement une charge électrique de l'hadron. De plus, l'interaction des photons énergétiques à protons est similaire à l'interaction des photons avec des neutrons en dépit du fait que les structures de charge électrique des protons et les neutrons sont sensiblement différentes.
Une théorie appelée Vector Meson Dominance (VMD) a été développé pour expliquer cet effet. Selon VMD, le photon est une superposition du photon pur électromagnétique (qui interagit uniquement avec des charges électriques) et méson vecteur.
Le photon comme un boson jauge
Le champ électromagnétique peut être comprise comme unchamp de jauge, soit comme un champ qui résulte d'exiger qu'une symétrie de jauge contient indépendamment à chaque position dans l'espace-temps. Pour le un champ électromagnétique, cette symétrie de jauge est leabélienU (1) de symétrie d'unnombre complexe, qui reflète la capacité de faire varier laphase d'un nombre complexe, sans affecterobservables oud'une valeur réelle des fonctionsqui en sont issus, tels que leénergieou leLagrangien.
Les quanta d'un champ de jauge abélien doit être sans masse, bosons non chargées, aussi longtemps que la symétrie est pas cassé; par conséquent, le photon est prévu pour être sans masse, et d'avoir zéro charge électrique et de spin entier. La forme particulière de l' interaction électromagnétique spécifie que le photon doit avoir de spin ± 1; Ainsi, son hélicité doit être  . Ces deux composantes de spin correspondent aux concepts classiques de la lumière polarisée circulairement droitier et gaucher. Cependant, les transitoires photons virtuels de l'électrodynamique quantique peuvent également adopter des états de polarisation non physiques.
. Ces deux composantes de spin correspondent aux concepts classiques de la lumière polarisée circulairement droitier et gaucher. Cependant, les transitoires photons virtuels de l'électrodynamique quantique peuvent également adopter des états de polarisation non physiques.
Dans le règne Modèle Standard de la physique, le photon est l'un des quatre bosons de jauge à l' interaction électrofaible; la les trois autres sont désignés W + , W - et Z 0 et sont responsables de la interaction faible. différence de la photonique, ces bosons de jauge ont de masse, en raison d'un mécanisme qui rompt leur SU (2) symétrie de jauge. L'unification du photon avec bosons de jauge W et Z dans l'interaction électrofaible a été accompli par Sheldon Glashow, Abdus Salam et Steven Weinberg, pour lesquels elles ont été attribuées de 1979 Prix Nobel de physique. physiciens continuent à émettre l'hypothèse grandes théories unifiées qui relient ces quatre bosons de jauge avec les huit bosons de jauge de gluons de la chromodynamique quantique; Toutefois, les prévisions clés de ces théories, comme la désintégration du proton, n'a pas été observé expérimentalement.
Contributions à la masse d'un système
L'énergie d'un système qui émet un photon est diminué par l'énergie 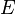 du photon, telle que mesurée dans le cadre du système d'émission de repos, ce qui peut entraîner une réduction de la masse de la quantité
du photon, telle que mesurée dans le cadre du système d'émission de repos, ce qui peut entraîner une réduction de la masse de la quantité 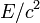 . De même, la masse d'un système qui absorbe un photon est augmenté d'un montant correspondant. Comme application, le bilan énergétique de réactions nucléaires impliquant des photons est généralement écrit en termes de masses des noyaux impliqués, et les termes de la forme
. De même, la masse d'un système qui absorbe un photon est augmenté d'un montant correspondant. Comme application, le bilan énergétique de réactions nucléaires impliquant des photons est généralement écrit en termes de masses des noyaux impliqués, et les termes de la forme 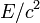 pour les photons gamma (et pour d'autres énergies concernées, telles que l'énergie de recul des noyaux).
pour les photons gamma (et pour d'autres énergies concernées, telles que l'énergie de recul des noyaux).
Ce concept est appliqué dans les prédictions clés de l'électrodynamique quantique (QED, voir ci-dessus). Dans cette théorie, la masse des électrons (ou, plus généralement, les leptons) est modifiée en incluant les contributions de masse de photons virtuels, dans une technique appelée renormalisation . Ces «corrections radiatives" contribuent à un certain nombre de prédictions de QED, tels que le moment magnétique dipolaire de leptons, le déplacement de Lamb, et la structure hyperfine de paires de leptons consolidés, tels que muonium et positronium.
Depuis photons contribuent à la tenseur-énergie, ils exercent une attraction gravitationnelle sur d'autres objets, selon la théorie de la relativité générale . A l'inverse, les photons sont eux-mêmes affectés par la gravité; leurs trajectoires normalement droites peuvent être pliés par déformé l'espace-temps, comme dans l'effet de lentille gravitationnelle, et leurs fréquences peuvent être réduites en passant à un plus haut potentiel gravitationnel, comme dans l' expérience Pound-Rebka. Cependant, ces effets ne sont pas spécifiques aux photons; exactement les mêmes effets seraient prévus pour classiques ondes électromagnétiques .
Photons dans la matière
Toute «explication» de la façon dont les photons voyagent à travers la matière doit expliquer pourquoi différents arrangements de la matière sont transparent ou opaque à différentes longueurs d'onde (lumière à travers carbone diamant ou pas, comme le graphite) et pourquoi photons individuels se comportent de la même manière que les grands groupes. Explications qui invoquent «absorption» et «re-émission» doivent fournir une explication pour la directionnalité des photons (diffraction, réflexion) et expliquer davantage comment paires de photons intriqués peuvent voyager à travers la matière sans leur état ??????quantique effondrement.
L'explication la plus simple est que la lumière qui se déplace à travers la matière transparente fait à une vitesse inférieure à c , la vitesse de la lumière dans le vide. En outre, la lumière peut également subir diffusion et absorption. Il ya des circonstances dans lesquelles le transfert de chaleur à travers un matériau est essentiellement radiatif, impliquant l'émission et l'absorption des photons en son sein. Un exemple serait dans le noyau du Soleil L'énergie peut prendre environ un million d'années pour atteindre la surface. Toutefois, ce phénomène est distinct du rayonnement diffusé de manière diffuse passant à travers la matière, car elle implique l'équilibre local entre le rayonnement et la température. Ainsi, le temps est le temps qu'il faut l' énergie doit être transférée, et non pas les photons eux-mêmes. Une fois dans l'espace ouvert, un photon du Soleil prend seulement 8,3 minutes pour atteindre la Terre. Le facteur par lequel la vitesse de la lumière est réduite dans une matière est appelée indice de réfraction du matériau. Dans une image d'onde classique, le ralentissement peut être expliqué par la lumière inductrice polarisation électrique en la matière, la question polarisée rayonnant nouvelle lumière, et la lumière nouvelle interférer avec l'onde lumineuse d'origine pour former une onde retardée. Dans une image de particules, le ralentissement peut à la place être décrite comme un mélange du photon excitation quantique de la matière ( quasi-particules telles que les phonons et excitons) pour former un polaritons; ce polaritons a une valeur non nulle masse effective, ce qui signifie qu'il ne peut pas voyager à c .
Alternativement, les photons peuvent être considérés comme toujours voyager à c , même dans la matière, mais ils ont leur déphasé (retardé ou avancé) lors de l'interaction avec les disperse atomiques: cela modifie leur longueur d'onde et de l'élan, mais pas accélérer. Une onde lumineuse composée de ces photons ne voyage plus lent que la vitesse de la lumière. Dans cette vue, les photons sont «nu», et sont dispersés et déphasés, tandis que dans la vue de l'alinéa précédent les photons sont «habillés» par leur interaction avec la matière, et se déplacent sans diffusion ou décalage de phase, mais à une vitesse inférieure .
La lumière de différentes fréquences peut voyager à travers la matière à des vitesses différentes; cela se appelle dispersion. Dans certains cas, il peut en résulter des vitesses très lentes de la lumière dans la matière. Les effets des interactions des photons avec d'autres quasi particules peuvent être observées directement dans la diffusion Raman et diffusion de Brillouin.
Photons peuvent également être absorbés par des noyaux, des atomes ou des molécules, provoquant des transitions entre leur les niveaux d'??nergie. Un exemple classique est la transition moléculaire de la rétine C 20 H 28 O, qui est responsable de la vision, comme l'a découvert en 1958 par le prix Nobel biochimiste George Wald et collègues. L'absorption provoque une cis-trans d'isomérisation qui, en combinaison avec d'autres telles transitions, est transduit dans des influx nerveux. L'absorption de photons peut même briser les liaisons chimiques, comme dans le photodissociation de chlore ; cela est l'objet de la photochimie. De manière analogue, les rayons gamma peuvent dans certaines circonstances dissocier noyaux atomiques dans un processus appelé photodésintégration.
Les applications technologiques
Photons ont de nombreuses applications dans la technologie. Ces exemples sont choisis pour illustrer les applications de photons en soi , plutôt que de dispositifs optiques généraux tels que des lentilles, etc., qui pourraient fonctionner en vertu d'une théorie classique de la lumière. Le laser est une application très importante et il est discuté ci-dessus sous l'??mission stimul??e.
Photons individuels peuvent être détectées par diverses méthodes. Le classique tube photomultiplicateur exploite l' effet photoélectrique: un atterrissage de photons sur une plaque de métal éjecte un électron, l'ouverture d'une avalanche jamais amplification d'électrons. copeaux de Charge-Coupled Device utilisent un effet similaire dans les semi-conducteurs : un photon incident génère une charge sur un microscope condensateur qui peut être détectée. D'autres détecteurs tels que les compteurs Geiger utilisent la capacité de photons pour ioniser les molécules de gaz, ce qui provoque un changement détectable de conductivité.
La formule de l'énergie de Planck est souvent utilisé par les ingénieurs et les chimistes dans la conception, à la fois pour calculer la variation d'énergie résultant d'une absorption de photons et de prédire la fréquence de la lumière émise pour une énergie donnée transition. Par exemple, le spectre d'émission d'uneampoule fluorescente peut être conçu en utilisant des molécules de gaz différents avec des niveaux d'énergie électronique et en ajustant l'énergie typique avec un électron qui frappe les molécules de gaz à l'intérieur de l'ampoule.
est souvent utilisé par les ingénieurs et les chimistes dans la conception, à la fois pour calculer la variation d'énergie résultant d'une absorption de photons et de prédire la fréquence de la lumière émise pour une énergie donnée transition. Par exemple, le spectre d'émission d'uneampoule fluorescente peut être conçu en utilisant des molécules de gaz différents avec des niveaux d'énergie électronique et en ajustant l'énergie typique avec un électron qui frappe les molécules de gaz à l'intérieur de l'ampoule.
Sous certaines conditions, une transition énergétique peut être excité par «deux» photons qui, individuellement, sont jugées insuffisantes. Ceci permet pour une meilleure résolution de la microscopie, parce que l'échantillon absorbe de l'énergie seulement dans la région où deux faisceaux de couleurs différentes se chevauchent de manière significative, ce qui peut être rendu beaucoup plus petit que le volume d'excitation d'un faisceau unique (voir excitation à deux photons microscopie). En outre, ces photons provoquent moins de dommages à l'échantillon, car ils sont de plus faible énergie.
Dans certains cas, deux transitions d'énergie peuvent être couplés de telle sorte que, comme un seul système absorbe un photon, à proximité d'un autre système "vole" son énergie et réémet un photon d'une fréquence différente. Ceci est la base de transfert d'énergie de résonance de fluorescence, une technique qui est utilisée en biologie moléculaire pour étudier l'interaction de appropriées des protéines .
Plusieurs types de matériel générateur de nombres aléatoires impliquent la détection de photons uniques. Dans un exemple, pour chaque bit dans la séquence aléatoire qui doit être produit, un photon est envoyé à un séparateur de faisceau. Dans une telle situation, il ya deux résultats possibles de probabilité égale. Le résultat réel est utilisé pour déterminer si le bit suivant dans la séquence est "0" ou "1".
Des recherches r??centes
Beaucoup de recherches ont été consacrées aux applications de photons dans le domaine de l'optique quantique. Les photons semblent bien adaptés pour être les éléments d'une extrêmement rapide ordinateur quantique , et l' intrication quantique de photons est un centre de recherche. procédés optiques non linéaires sont un autre domaine de recherche actif, avec des sujets tels que l'absorption à deux photons, auto-modulation de phase, instabilité de modulation et oscillateurs paramétriques optiques. Cependant, de tels procédés ne nécessitent généralement pas l'hypothèse de photons en tant que tels ; ils peuvent souvent être modélisés en traitant atomes que les oscillateurs non linéaires. Le processus non linéaire de conversion paramétrique spontanée est souvent utilisé pour produire des états de photons uniques. Enfin, les photons sont essentielles dans certains aspects de la communication optique, en particulier pour la cryptographie quantique.