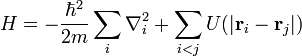Th??orie quantique des champs
Contexte des ??coles Wikip??dia
SOS Enfants a fait cette s??lection Wikipedia aux c??t??s d'autres ??coles des ressources . Visitez le site Web d'enfants SOS au http://www.soschildren.org/
| Th??orie quantique des champs |
|---|
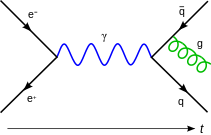 Diagramme de Feynman |
| Histoire |
Fond
|
Sym??tries
|
Outils
|
??quations
|
|
Th??ories incompl??tes
|
Les scientifiques
|
La th??orie quantique des champs (QFT) est un cadre th??orique pour la construction m??canique quantique mod??les de terrain comme les syst??mes ou, de fa??on ??quivalente, des syst??mes ?? plusieurs corps. Il est largement utilis?? dans la physique des particules et de la physique de la mati??re condens??e . La plupart des th??ories en physique des particules moderne, y compris le mod??le standard des particules ??l??mentaires et leurs interactions, sont formul??es comme relativistes th??ories quantiques des champs. En mati??re condens??e, th??ories de champ quantiques sont utilis??s dans de nombreuses circonstances, notamment celles o?? le nombre de particules est autoris?? ?? varier, par exemple, dans le La th??orie BCS de la supraconductivit?? .
Histoire
Th??orie quantique des champs origine dans le 1920 du probl??me de la cr??ation d'une th??orie quantique de la champ ??lectromagn??tique. En 1926 , Max Born, Pascual Jordanie et Werner Heisenberg construit une telle th??orie en exprimant le domaine de interne degr??s de libert?? comme un ensemble infini de oscillateurs harmoniques et en utilisant la proc??dure habituelle pour quantifier ces oscillateurs ( quantification canonique). Cette th??orie suppose qu'aucune accusation ou courants ??lectriques ??taient pr??sents et qu'on appellerait aujourd'hui un la th??orie en champ libre. La premi??re th??orie assez compl??te ??lectrodynamique quantique, qui comprenait ?? la fois le champ ??lectromagn??tique et charg??es ??lectriquement la mati??re (en particulier, ??lectrons ) comme des objets de la m??canique quantique, a ??t?? cr???? par Paul Dirac en 1927 . Cette th??orie quantique des champs pourrait ??tre utilis?? pour mod??liser les processus importants tels que l'??mission d'un photon par un ??lectron tomber dans un ??tat quantique d'??nergie inf??rieure, un processus dans lequel le nombre de particules change - un atome ?? l'??tat initial devient un atome plus un photon dans l'??tat final. Il est d??sormais entendu que la capacit?? de d??crire ces processus est l'un des aspects les plus importants de la th??orie quantique des champs.
Il ??tait ??vident d??s le d??but que un traitement quantique correcte du champ ??lectromagn??tique devait int??grer en quelque sorte d'Einstein relativit?? la th??orie, qui avait apr??s tout d??velopp?? ?? partir de l'??tude des ??lectromagn??tisme classique. Cette n??cessit?? de mettre sur pied la relativit?? et la m??canique quantique ??tait la deuxi??me motivation majeure dans le d??veloppement de la th??orie quantique des champs. Pascual Jordanie et Wolfgang Pauli a montr?? dans 1928 que les champs quantiques pourraient ??tre apport??es ?? se comporter de la fa??on pr??dite par la relativit?? restreinte cours transformations de coordonn??es (en particulier, ils ont montr?? que le domaine commutateurs ??taient Lorentz invariant), et 1933 Niels Bohr et Leon Rosenfeld a montr?? que ce r??sultat pourrait ??tre interpr??t?? comme une limitation de la capacit?? ?? mesurer les champs au s??parations comme l'espace, exactement comme requis par la relativit??. Un nouvel ??lan pour la th??orie quantique des champs est venu avec la d??couverte de la ??quation de Dirac, une ??quation simple particules ob??issant ?? la fois la relativit?? et la m??canique quantique, quand il a ??t?? d??montr?? que plusieurs de ses propri??t??s ind??sirables (tels que les ??tats ?? ??nergie n??gative) pourrait ??tre ??limin?? en reformulant l'??quation de Dirac comme une th??orie quantique des champs. Ce travail a ??t?? effectu?? par Wendell Furry, Robert Oppenheimer , Vladimir Fock, et d'autres.
Le troisi??me fil dans le d??veloppement de la th??orie quantique des champs ??tait la n??cessit?? de manipuler les statistiques de syst??mes ?? plusieurs particules constamment et avec facilit??. En 1927 , la Jordanie a essay?? de prolonger la quantification canonique de champs aux fonctions d'onde ?? plusieurs corps de des particules identiques, une proc??dure qui est parfois appel?? seconde quantification. En 1928 , la Jordanie et Eugene Wigner a constat?? que le champ quantique d??crivant ??lectrons, ou autre fermions, devaient ??tre ??largi ?? l'aide anti-navette op??rateurs de cr??ation et d'annihilation en raison de la Principe d'exclusion de Pauli. Ce fil du d??veloppement a ??t?? incorpor?? dans la th??orie ?? plusieurs corps, et fortement influenc??es physique de la mati??re condens??e et la physique nucl??aire .
Malgr?? ses premiers succ??s, la th??orie quantique des champs a ??t?? en proie ?? plusieurs difficult??s th??oriques graves. Beaucoup de grandeurs physiques apparemment inoffensifs, tels-que le changement d'??nergie d'??tats ??lectroniques dus ?? la pr??sence du champ ??lectromagn??tique, ont donn?? l'infini - un r??sultat absurde - lorsqu'ils sont calcul??s en utilisant la th??orie quantique des champs. Ce ??probl??me de divergence" a ??t?? r??solu au cours de la Ann??es 1940 par Bethe, Tomonaga, Schwinger, Feynman , et Dyson, ?? travers la proc??dure dite de renormalisation . Cette phase de d??veloppement a culmin?? avec la construction de la th??orie moderne de ??lectrodynamique quantique (QED). ?? partir de la 1950 avec les travaux de Yang et Mills, QED a ??t?? g??n??ralis?? ?? une classe de th??ories quantiques des champs appel??s th??orie de jauge. Le 1960 et 1970 a vu la formulation d'une th??orie de jauge maintenant connu comme le mod??le standard de la physique des particules , qui d??crit toutes les particules ??l??mentaires connues et les interactions entre eux. Le faible partie de l'interaction du mod??le standard a ??t?? formul??e par Sheldon Glashow, avec le M??canisme de Higgs ajout??e par Steven Weinberg et Abdus Salam. La th??orie est r??v??l?? ??tre conforme par Gerardus 't Hooft et Martinus Veltman.
??galement au cours de la 1970, les d??veloppements parall??les dans l'??tude de transitions de phase dans la mati??re condens??e conduit Leo Kadanoff, Michael Fisher et Kenneth Wilson (l'extension du travail de Ernst Stueckelberg, Andre Peterman, Murray Gell-Mann et Francis Low) ?? un ensemble d'id??es et de m??thodes connu sous le nom groupe de renormalisation. En fournissant une meilleure compr??hension de la physique de la proc??dure de renormalisation invent?? dans le 1940, le groupe de renormalisation d??clench?? ce qu'on a appel?? la ??grande synth??se" de la physique th??orique, unissant les techniques th??oriques de terrain quantique utilis??s en physique des particules et de la physique de la mati??re condens??e dans un cadre th??orique unique.
L'??tude de la th??orie quantique des champs est vivante et florissante, comme le sont les applications de cette m??thode ?? de nombreux probl??mes physiques. Il reste l'un des domaines les plus vitaux de physique th??orique aujourd'hui, fournissant un langage commun ?? de nombreuses branches de la physique .
Principes de la th??orie quantique des champs
Champs classiques et quantiques des champs
La m??canique quantique , dans sa formulation la plus g??n??rale, est une th??orie de l'abstrait op??rateurs (observables) agissant sur un espace d'??tat abstrait ( Espace de Hilbert), o?? les observables repr??sentent des quantit??s physiquement observables et l'espace d'??tat repr??sente les ??tats possibles du syst??me ?? l'??tude. En outre, chaque observable correspond, dans un sens technique, ?? l'id??e classique d'une degr?? de libert??. Par exemple, les observables fondamentales associ??es ?? la requ??te d'une seule particule de la m??canique quantique sont les op??rateurs position et impulsion 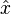 et
et 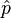 . La m??canique quantique ordinaires offres avec des syst??mes de ce genre, qui poss??dent un petit ensemble de degr??s de libert??.
. La m??canique quantique ordinaires offres avec des syst??mes de ce genre, qui poss??dent un petit ensemble de degr??s de libert??.
(Il est important de noter, ?? ce stade, que cet article ne utilise pas le mot " particule "dans le contexte de dualit?? onde-particule. En th??orie quantique des champs, "particule" est un terme g??n??rique pour toute entit?? m??canique quantique discret, comme un ??lectron, ce qui peut se comporter comme particules classiques ou vagues classiques dans diff??rentes conditions exp??rimentales.)
Un champ quantique est un syst??me m??canique quantique contenant une grande, et peut-??tre infini , le nombre de degr??s de libert??. Ce ne est pas aussi exotique une situation qu'on pourrait le penser. Un champ classique contient un ensemble de degr??s de libert?? ?? chaque point de l'espace; par exemple, le classique champ ??lectromagn??tique d??finit deux vecteurs - le champ ??lectrique et le champ magn??tique - qui peuvent, en principe, prendre des valeurs distinctes pour chaque position  . Lorsque le champ dans son ensemble est consid??r?? comme un syst??me m??canique quantique, ses observables forment un infini (en fait, uncountable) ensemble, parce
. Lorsque le champ dans son ensemble est consid??r?? comme un syst??me m??canique quantique, ses observables forment un infini (en fait, uncountable) ensemble, parce  est continue.
est continue.
En outre, les degr??s de libert?? dans un champ quantique sont dispos??s en s??ries "r??p??t??es". Par exemple, les degr??s de libert?? dans un champ ??lectromagn??tique peuvent ??tre regroup??s en fonction de la position  , Avec exactement deux vecteurs pour chaque
, Avec exactement deux vecteurs pour chaque  . Notez que
. Notez que  est un nombre ordinaire qui "index" les observables; il est ?? ne pas confondre avec l'op??rateur de position
est un nombre ordinaire qui "index" les observables; il est ?? ne pas confondre avec l'op??rateur de position 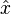 rencontr?? en m??canique quantique ordinaire, ce qui est une observable. (Ainsi, la m??canique quantique ordinaire est parfois appel??s ??th??orie z??ro-dimensionnel quantique des champs", car il ne contient qu'un seul ensemble d'observables.) Il est ??galement important de noter qu'il n'y a rien de sp??cial
rencontr?? en m??canique quantique ordinaire, ce qui est une observable. (Ainsi, la m??canique quantique ordinaire est parfois appel??s ??th??orie z??ro-dimensionnel quantique des champs", car il ne contient qu'un seul ensemble d'observables.) Il est ??galement important de noter qu'il n'y a rien de sp??cial  parce que, comme il se av??re, il ya g??n??ralement plus d'une fa??on d'indexer les degr??s de libert?? dans le domaine.
parce que, comme il se av??re, il ya g??n??ralement plus d'une fa??on d'indexer les degr??s de libert?? dans le domaine.
Dans les sections suivantes, nous allons montrer comment ces id??es peuvent ??tre utilis??s pour construire une th??orie de la m??canique quantique avec les propri??t??s souhait??es. Nous allons commencer par discuter une particule m??canique quantique et la th??orie associ??e d'un grand nombre de particules m??canique quantique. Puis, en trouvant un moyen d'indexer les degr??s de libert?? dans le probl??me du nombre de particules, nous allons construire un champ quantique et d'??tudier ses implications.
Single-particules et plusieurs particules m??canique quantique
En m??canique quantique ordinaire, le temps d??pendant ??quation de Schr??dinger d??crivant le mouvement d'une particule non relativiste est
o?? 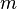 est de la particule de masse ,
est de la particule de masse ,  est l'appliqu?? potentiel, et
est l'appliqu?? potentiel, et  d??signe le ??tat quantique (nous utilisons Notation bra-ket).
d??signe le ??tat quantique (nous utilisons Notation bra-ket).
Nous voulons consid??rer comment ce probl??me se g??n??ralise ??  particules. Il ya deux motivations pour ??tudier le probl??me plusieurs particules. Le premier est un besoin simple dans la physique condens??e de mati??re , o?? en g??n??ral le nombre de particules est de l'ordre de nombre d'Avogadro (6.0221415 x 10 23). La deuxi??me motivation pour le probl??me plusieurs particules provient de la physique des particules et le d??sir d'int??grer les effets de la relativit?? restreinte . Si l'on tente d'inclure le relativiste ??nergie reste dans l'??quation ci-dessus, le r??sultat est soit le Klein-Gordon ??quation ou le ??quation de Dirac. Cependant, ces ??quations ont de nombreuses qualit??s insatisfaisants; par exemple, ils poss??dent l'??nergie valeurs propres qui se ??tendent sur -∞, de sorte qu'il semble y avoir aucune d??finition simple d'un ??tat fondamental. Il se av??re que ces incoh??rences proviennent de n??gliger la possibilit?? de cr??er ou de d??truire les particules dynamique, ce qui est un aspect crucial de la relativit??. Einstein c??l??bre rapport masse-??nergie pr??dit que les particules suffisamment massives peuvent se d??sint??grer en plusieurs particules plus l??g??res, et suffisamment particules ??nerg??tiques peuvent se combiner pour former des particules massives. Par exemple, un ??lectron et un positron peut annihiler l'un l'autre pour cr??er des photons . Ainsi, une th??orie quantique relativiste coh??rent doit ??tre formul??e comme une th??orie plusieurs particules.
particules. Il ya deux motivations pour ??tudier le probl??me plusieurs particules. Le premier est un besoin simple dans la physique condens??e de mati??re , o?? en g??n??ral le nombre de particules est de l'ordre de nombre d'Avogadro (6.0221415 x 10 23). La deuxi??me motivation pour le probl??me plusieurs particules provient de la physique des particules et le d??sir d'int??grer les effets de la relativit?? restreinte . Si l'on tente d'inclure le relativiste ??nergie reste dans l'??quation ci-dessus, le r??sultat est soit le Klein-Gordon ??quation ou le ??quation de Dirac. Cependant, ces ??quations ont de nombreuses qualit??s insatisfaisants; par exemple, ils poss??dent l'??nergie valeurs propres qui se ??tendent sur -∞, de sorte qu'il semble y avoir aucune d??finition simple d'un ??tat fondamental. Il se av??re que ces incoh??rences proviennent de n??gliger la possibilit?? de cr??er ou de d??truire les particules dynamique, ce qui est un aspect crucial de la relativit??. Einstein c??l??bre rapport masse-??nergie pr??dit que les particules suffisamment massives peuvent se d??sint??grer en plusieurs particules plus l??g??res, et suffisamment particules ??nerg??tiques peuvent se combiner pour former des particules massives. Par exemple, un ??lectron et un positron peut annihiler l'un l'autre pour cr??er des photons . Ainsi, une th??orie quantique relativiste coh??rent doit ??tre formul??e comme une th??orie plusieurs particules.
En outre, nous allons supposer que le  particules sont indiscernables. Comme il est d??crit dans l'article sur particules identiques, ce qui implique que l'??tat de l'ensemble du syst??me doit ??tre soit sym??trique ( bosons) ou antisym??trique ( fermions) lorsque les coordonn??es de ses particules constitutives sont ??chang??s. Ces ??tats multi-particules sont assez compliqu??es ?? ??crire. Par exemple, l'??tat quantique d'un syst??me g??n??ral de
particules sont indiscernables. Comme il est d??crit dans l'article sur particules identiques, ce qui implique que l'??tat de l'ensemble du syst??me doit ??tre soit sym??trique ( bosons) ou antisym??trique ( fermions) lorsque les coordonn??es de ses particules constitutives sont ??chang??s. Ces ??tats multi-particules sont assez compliqu??es ?? ??crire. Par exemple, l'??tat quantique d'un syst??me g??n??ral de  bosons se ??crit
bosons se ??crit
o?? 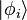 sont les ??tats ?? une particule,
sont les ??tats ?? une particule,  est le nombre de particules Etat occupant
est le nombre de particules Etat occupant  Et la somme est calcul??e sur tous les possibles permutations
Et la somme est calcul??e sur tous les possibles permutations 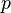 agissant sur
agissant sur  ??l??ments. En g??n??ral, ce est une somme de
??l??ments. En g??n??ral, ce est une somme de  (
(  factorielle ) Les termes distincts, ce qui devient vite ing??rable
factorielle ) Les termes distincts, ce qui devient vite ing??rable  augmente. Le moyen de simplifier ce probl??me est d'en faire une th??orie quantique des champs.
augmente. Le moyen de simplifier ce probl??me est d'en faire une th??orie quantique des champs.
Deuxi??me quantification
Dans cette section, nous allons d??crire une m??thode pour construire une th??orie quantique des champs appel?? seconde quantification. Il se agit essentiellement de choisir une fa??on d'indexer les degr??s de libert?? de la m??canique quantique en l'espace de plusieurs ??tats-particules identiques. Il est bas?? sur la Formulation hamiltonien de la m??canique quantique; plusieurs autres approches existent, comme le Feynman chemin int??grante, qui utilise une Formulation lagrangienne. Pour un aper??u, voir l'article sur quantification.
Seconde quantification de bosons
Pour plus de simplicit??, nous allons d'abord discuter de seconde quantification pour bosons, qui forment ??tats quantiques parfaitement sym??triques. Notons les ??tats unique de particules mutuellement orthogonaux par  et ainsi de suite. Par exemple, l'??tat 3-particule avec une particule dans l'??tat
et ainsi de suite. Par exemple, l'??tat 3-particule avec une particule dans l'??tat 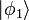 et deux dans l'??tat
et deux dans l'??tat 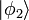 est
est
La premi??re ??tape de la seconde quantification est d'exprimer ces ??tats quantiques en termes de nombres d'occupation, en ??num??rant le nombre de particules occupant chacun des ??tats ?? une particule  etc. Ce est simplement une autre fa??on d'??tiqueter les Etats. Par exemple, l'??tat de particules 3 ci-dessus est d??sign??e par
etc. Ce est simplement une autre fa??on d'??tiqueter les Etats. Par exemple, l'??tat de particules 3 ci-dessus est d??sign??e par
L'??tape suivante consiste ?? ??tendre le  espace -particle de l'Etat ?? inclure les espaces de l'??tat pour toutes les valeurs possibles de
espace -particle de l'Etat ?? inclure les espaces de l'??tat pour toutes les valeurs possibles de  . Cet espace d'??tat ??tendu, connu sous le nom Espace de Fock, est compos?? de l'espace d'??tat d'un syst??me sans particules (le soi-disant ??tat de vide), plus l'espace d'??tat d'un syst??me 1-particules, plus l'espace d'??tat d'un syst??me 2-particules, et ainsi de suite. Il est facile de voir qu'il ya une correspondance un-??-un entre la repr??sentation de nombre d'occupation et les Etats bosons valables dans l'espace Fock.
. Cet espace d'??tat ??tendu, connu sous le nom Espace de Fock, est compos?? de l'espace d'??tat d'un syst??me sans particules (le soi-disant ??tat de vide), plus l'espace d'??tat d'un syst??me 1-particules, plus l'espace d'??tat d'un syst??me 2-particules, et ainsi de suite. Il est facile de voir qu'il ya une correspondance un-??-un entre la repr??sentation de nombre d'occupation et les Etats bosons valables dans l'espace Fock.
?? ce stade, le syst??me m??canique quantique est devenue un champ quantique dans le sens que nous avons d??crit ci-dessus. Degr??s ??l??mentaires du domaine de la libert?? sont les nombres d'occupation, et chaque nombre d'occupation est index?? par un certain nombre  , Indiquant lequel des ??tats ?? une particule
, Indiquant lequel des ??tats ?? une particule 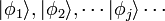 il se r??f??re.
il se r??f??re.
Les propri??t??s de ce champ quantique peuvent ??tre explor??es en d??finissant cr??ation et d'annihilation op??rateurs, qui ajoutent et les particules de la soustraction. Ils sont analogues aux ??op??rateurs d'??chelle" dans le probl??me de oscillateur harmonique quantique, qui a ajout?? et soustrait quanta d'??nergie. Toutefois, ces op??rateurs cr??ent litt??ralement et annihilent des particules d'un ??tat quantique donn??. L'op??rateur d'annihilation de bosons  et exploitant de cr??ation
et exploitant de cr??ation  avoir les effets suivants:
avoir les effets suivants:
On peut montrer que ce sont les op??rateurs dans le sens de la m??canique quantique d'habitude, ce est ?? dire op??rateurs lin??aires agissant sur l'espace de Fock. En outre, ils sont en effet Conjugu??s hermitiques, ce qui justifie la fa??on dont nous les avons ??crite. Ils peuvent ??tre pr??sent??s ?? ob??ir ?? la relation de commutation
o??  Supports pour les Kronecker. Ce sont pr??cis??ment les relations ob??i par les op??rateurs d'??chelle pour un ensemble infini de ind??pendante oscillateurs harmoniques quantiques, une pour chaque ??tat ?? une particule. Ajout ou suppression de bosons de chaque Etat est donc analogue ?? excitant ou de-excitation d'un quantum d'??nergie dans un oscillateur harmonique.
Supports pour les Kronecker. Ce sont pr??cis??ment les relations ob??i par les op??rateurs d'??chelle pour un ensemble infini de ind??pendante oscillateurs harmoniques quantiques, une pour chaque ??tat ?? une particule. Ajout ou suppression de bosons de chaque Etat est donc analogue ?? excitant ou de-excitation d'un quantum d'??nergie dans un oscillateur harmonique.
Le Hamiltonien du champ quantique (qui, par la ??quation de Schr??dinger, d??termine sa dynamique) peuvent ??tre ??crites en termes d'op??rateurs de cr??ation et d'annihilation. Par exemple, l'hamiltonien d'un champ de libres (sans interaction) est bosons
o??  est l'??nergie de la
est l'??nergie de la 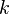 i??me une particule ??tat propre de l'??nergie. Notez que
i??me une particule ??tat propre de l'??nergie. Notez que
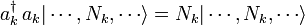 .
.
Seconde quantification de fermions
Il se av??re que une d??finition diff??rente de la cr??ation et l'annihilation doit ??tre utilis?? pour d??crire fermions. Selon le Principe d'exclusion de Pauli, fermions ne peut pas partager ??tats quantiques, de sorte que leurs nombres d'occupation  ne peut prendre la valeur 0 ou 1. Les op??rateurs d'annihilation fermioniques
ne peut prendre la valeur 0 ou 1. Les op??rateurs d'annihilation fermioniques  et op??rateurs de cr??ation
et op??rateurs de cr??ation 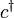 sont d??finis par
sont d??finis par
Ces ob??ir ?? un relation de anticommutation:
On peut remarquer ?? partir de ce que l'application d'un op??rateur de cr??ation fermionique donne deux fois z??ro, de sorte qu'il est impossible pour les particules ?? part les Etats ?? particule unique, en conformit?? avec le principe d'exclusion.
Les op??rateurs terrain
Nous avons d??j?? mentionn?? qu'il peut y avoir plus d'une fa??on d'indexer les degr??s de libert?? dans un champ quantique. Deuxi??me indices de quantification du terrain par l'??num??ration des ??tats quantiques ?? particule unique. Cependant, comme nous l'avons vu, il est plus naturel de penser ?? un ??champ??, comme le champ ??lectromagn??tique, comme un ensemble de degr??s de libert?? index?? par la position.
?? cette fin, nous pouvons d??finir des op??rateurs de terrain qui cr??ent ou d??truisent une particule ?? un point particulier dans l'espace. En physique des particules, ces op??rateurs se av??rent ??tre plus commode de travailler avec, parce qu'ils facilitent de formuler des th??ories qui satisfont aux exigences de la relativit??.
??tats particules uniques sont g??n??ralement ??num??r??s en fonction de leur moments (comme dans le particule dans un probl??me de bo??te.) Nous pouvons construire des op??rateurs de terrain en appliquant la Transform??e de Fourier aux op??rateurs de cr??ation et d'annihilation de ces Etats. Par exemple, l'op??rateur d'annihilation champ bosonique 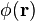 est
est
Les op??rateurs de terrain bosoniques ob??issent ?? la relation de commutation
o??  Supports pour les Fonction de Dirac. Comme pr??c??demment, les relations fermioniques sont les m??mes, avec les commutateurs remplac??s par anticommutators.
Supports pour les Fonction de Dirac. Comme pr??c??demment, les relations fermioniques sont les m??mes, avec les commutateurs remplac??s par anticommutators.
Il convient de souligner que l'op??rateur de champ ne est pas la m??me chose que d'une fonction d'onde mono-particules. Le premier est un op??rateur agissant sur l'espace de Fock, et celui-ci est juste un champ scalaire. Cependant, ils sont ??troitement li??s, et sont en effet couramment d??sign??es par le m??me symbole. Si nous avons un hamiltonien avec une repr??sentation de l'espace, dire
o?? les indices  et
et  courir sur toutes les particules, puis l'hamiltonien de la th??orie des champs est
courir sur toutes les particules, puis l'hamiltonien de la th??orie des champs est
Ce ressemble remarquablement ?? une expression de la valeur moyenne de l'??nergie, avec 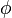 jouant le r??le de la fonction d'onde. Cette relation entre les op??rateurs sur le terrain et des fonctions d'onde, il est tr??s facile de formuler des th??ories sur le terrain ?? partir de Hamilton projet??e dans l'espace.
jouant le r??le de la fonction d'onde. Cette relation entre les op??rateurs sur le terrain et des fonctions d'onde, il est tr??s facile de formuler des th??ories sur le terrain ?? partir de Hamilton projet??e dans l'espace.
Implications de la th??orie quantique des champs
Unification des champs et des particules
La proc??dure "seconde de quantification" que nous avons d??crit dans la section pr??c??dente prend un ensemble d'??tats quantiques ?? particule unique comme point de d??part. Parfois, il est impossible de d??finir ces ??tats ?? une particule, et l'on doit se rendre directement ?? la th??orie quantique des champs. Par exemple, une th??orie quantique de la champ ??lectromagn??tique doit ??tre une th??orie quantique des champs, car il est impossible (pour diverses raisons) pour d??finir une fonction d'onde pour un seul photon . Dans de telles situations, la th??orie quantique des champs peut ??tre construit en examinant les propri??t??s m??caniques du domaine classique et deviner le la th??orie quantique correspondant. Les th??ories quantiques des champs obtenus de cette fa??on ont les m??mes propri??t??s que celles obtenues en utilisant la seconde quantification, cette cr??ation bien d??fini et op??rateurs d'annihilation ob??issant commutation ou anticommutation relations.
Th??orie quantique des champs fournit donc un cadre unifi?? pour d??crire les objets "sur le terrain-like" (tels que le champ ??lectromagn??tique, dont les excitations sont photons) et des objets "de particules-like" (telles que des ??lectrons, qui sont trait??s comme des excitations d'un champ ??lectronique sous-jacente ).
Signification physique de indiscernabilit?? des particules
La seconde proc??dure de quantification d??pend essentiellement de particules ??tant identiques. Nous ne aurions pas ??t?? en mesure de construire une th??orie quantique des champs d'un syst??me plusieurs particules distinguer, car il n'y aurait pas eu moyen de s??parer et en indexant les degr??s de libert??.
Beaucoup de physiciens pr??f??rent prendre l'interpr??tation inverse, qui est que la th??orie quantique des champs, explique ce que sont les particules identiques. En m??canique quantique ordinaire, il ne ya pas beaucoup de motivation th??orique de l'utilisation sym??trique (bosons) ou des ??tats antisym??triques (fermions), et la n??cessit?? pour ces pays est tout simplement consid??r?? comme un fait empirique. Du point de vue de la th??orie quantique des champs, les particules sont identiques si et seulement si ils sont excitations du m??me champ quantique sous-jacent. Ainsi, la question ??pourquoi sont tous les ??lectrons identiques?" provient de tort au sujet ??lectrons individuels comme des objets fondamentaux, alors qu'en fait ce ne est que le champ d'??lectrons qui est fondamental.
conservation de particules et non-conservation
Au cours de la seconde quantification, nous avons commenc?? avec un espace de hamiltonien et ??tat d??crivant un nombre fixe de particules (  ), Et se est termin??e avec un hamiltonien et de l'espace de l'Etat pour un nombre arbitraire de particules. Bien s??r, dans de nombreuses situations ordinaires
), Et se est termin??e avec un hamiltonien et de l'espace de l'Etat pour un nombre arbitraire de particules. Bien s??r, dans de nombreuses situations ordinaires  est une quantit?? importante et parfaitement bien d??finie, par exemple, si nous d??crivons un gaz atomes scell??s dans une bo??te. Du point de vue de la th??orie quantique des champs, de telles situations sont d??crites par les ??tats quantiques qui sont des ??tats propres de la op??rateur de num??ro
est une quantit?? importante et parfaitement bien d??finie, par exemple, si nous d??crivons un gaz atomes scell??s dans une bo??te. Du point de vue de la th??orie quantique des champs, de telles situations sont d??crites par les ??tats quantiques qui sont des ??tats propres de la op??rateur de num??ro 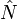 , Qui mesure le nombre total de particules pr??sentes. Comme pour toute observable de la m??canique quantique,
, Qui mesure le nombre total de particules pr??sentes. Comme pour toute observable de la m??canique quantique, 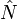 est conserv??e si elle commute avec l'hamiltonien. Dans ce cas, l'??tat quantique est pi??g?? dans le
est conserv??e si elle commute avec l'hamiltonien. Dans ce cas, l'??tat quantique est pi??g?? dans le  -particle sous-espace de l'espace de Fock totale, et la situation pourrait tout aussi bien ??tre d??crit par ordinaire
-particle sous-espace de l'espace de Fock totale, et la situation pourrait tout aussi bien ??tre d??crit par ordinaire  la m??canique quantique -particle.
la m??canique quantique -particle.
Par exemple, nous pouvons voir que l'hamiltonien libre de Higgs d??crit ci-dessus conserve nombre de particules. Chaque fois que l'hamiltonien fonctionne sur un ??tat, chaque particule d??truite par un op??rateur d'annihilation  est imm??diatement remis par l'op??rateur de cr??ation
est imm??diatement remis par l'op??rateur de cr??ation 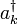 .
.
D'autre part, il est possible, et m??me commune, de rencontrer des ??tats quantiques qui ne sont pas ??tats propres de 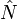 Qui ne ont pas un nombre de particules bien d??finies. Ces ??tats sont difficiles ou impossibles ?? g??rer en utilisant la m??canique quantique ordinaires, mais ils peuvent ??tre facilement d??crits dans la th??orie quantique des champs que superpositions quantiques des Etats ayant des valeurs diff??rentes de
Qui ne ont pas un nombre de particules bien d??finies. Ces ??tats sont difficiles ou impossibles ?? g??rer en utilisant la m??canique quantique ordinaires, mais ils peuvent ??tre facilement d??crits dans la th??orie quantique des champs que superpositions quantiques des Etats ayant des valeurs diff??rentes de  . Par exemple, supposons que nous ayons un champ bosonique dont les particules peuvent ??tre cr????s ou d??truits par des interactions avec un champ fermionique. Le hamiltonien du syst??me combin?? serait donn??e par les hamiltoniens du boson libre et les champs de fermions libres, plus une "??nergie potentielle" terme comme
. Par exemple, supposons que nous ayons un champ bosonique dont les particules peuvent ??tre cr????s ou d??truits par des interactions avec un champ fermionique. Le hamiltonien du syst??me combin?? serait donn??e par les hamiltoniens du boson libre et les champs de fermions libres, plus une "??nergie potentielle" terme comme
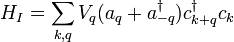 ,
,
o?? 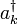 et
et  d??signe les op??rateurs de cr??ation et d'annihilation de bosons,
d??signe les op??rateurs de cr??ation et d'annihilation de bosons,  et
et  d??signe les op??rateurs de cr??ation et d'annihilation de fermions, et
d??signe les op??rateurs de cr??ation et d'annihilation de fermions, et 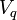 est un param??tre qui d??crit la force de l'interaction. Cette ??terme d'interaction" d??crit les processus dans lequel un fermion dans l'??tat
est un param??tre qui d??crit la force de l'interaction. Cette ??terme d'interaction" d??crit les processus dans lequel un fermion dans l'??tat 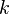 soit absorbe ou ??met un boson, ??tant ainsi un coup de pied dans un ??tat propre diff??rente
soit absorbe ou ??met un boson, ??tant ainsi un coup de pied dans un ??tat propre diff??rente 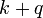 . (En fait, ce type de hamiltonien est utilis?? pour d??crire l'interaction entre ??lectrons de conduction et phonons dans les m??taux . L'interaction entre des ??lectrons et des photons est trait?? d'une mani??re similaire, mais est un peu plus compliqu??, car le r??le de pirouette doit ??tre prise en compte.) Une chose ?? noter ici est que m??me si nous commen??ons avec un nombre fixe de bosons, nous allons g??n??ralement retrouver avec une superposition d'??tats avec des nombres diff??rents de bosons ?? des moments plus tard. Le nombre de fermions, cependant, est conserv??e dans ce cas.
. (En fait, ce type de hamiltonien est utilis?? pour d??crire l'interaction entre ??lectrons de conduction et phonons dans les m??taux . L'interaction entre des ??lectrons et des photons est trait?? d'une mani??re similaire, mais est un peu plus compliqu??, car le r??le de pirouette doit ??tre prise en compte.) Une chose ?? noter ici est que m??me si nous commen??ons avec un nombre fixe de bosons, nous allons g??n??ralement retrouver avec une superposition d'??tats avec des nombres diff??rents de bosons ?? des moments plus tard. Le nombre de fermions, cependant, est conserv??e dans ce cas.
En mati??re condens??e , pr??cise avec des num??ros de particules mal d??finis sont particuli??rement importantes pour d??crire les diff??rents superfluides. Beaucoup des caract??ristiques d??terminantes d'un superfluide d??coulent de l'id??e que son ??tat quantique est une superposition d'??tats avec des nombres de particules diff??rentes.
Approches axiomatiques
La description pr??c??dente de la th??orie quantique des champs suit l'esprit dans lequel la plupart physiciens abordent le sujet. Cependant, il ne est pas math??matiquement rigoureuse. Au cours des derni??res d??cennies, il ya eu de nombreuses tentatives pour mettre la th??orie quantique des champs sur une base math??matique cabinet en formulant un ensemble de axiomes pour elle. Ces tentatives se r??partissent en deux grandes cat??gories.
La premi??re classe d'axiomes, d'abord propos?? au cours de la 1950, inclure le Wightman, Osterwalder-Schrader, et Syst??mes Haag-Kastler. Ils ont tent?? de formaliser la notion d'un ??champ de l'op??rateur-??valu??" des physiciens dans le cadre de analyse fonctionnelle, et un succ??s limit?? appr??ci??. Il ??tait possible de prouver que toute th??orie quantique des champs satisfaire ces axiomes satisfait certains th??or??mes g??n??raux, tels que le Th??or??me spin-statistique et de la Th??or??me CPT. Malheureusement, il se est av??r?? extr??mement difficile de montrer que toute la th??orie du champ r??aliste, y compris le mod??le standard , satisfait ces axiomes. La plupart des th??ories qui pourraient ??tre trait??es avec ces axiomes analytiques ??taient physiquement trivial, ??tre limit?? ?? de faibles dimensions et manquant dynamique int??ressante. La construction de th??ories qui satisfont l'un de ces ensembles d'axiomes tombe dans le domaine de th??orie quantique des champs constructive. Un travail important a ??t?? fait dans ce domaine dans le 1970 par Segal, Glimm, Jaffe et autres.
Pendant le 1980, une deuxi??me s??rie d'axiomes sur la base g??om??triques id??es a ??t?? propos??. Cette ligne d'enqu??te, ce qui limite son attention ?? une classe particuli??re des th??ories quantiques des champs appel??s th??ories topologiques des champs quantiques, est associ?? le plus ??troitement avec Michael Atiyah et Graeme Segal, et a notamment ??t?? compl??t??e par des Edward Witten, Richard Borcherds, et Maxim Kontsevich. Cependant, les th??ories quantiques des champs les plus physiquement pertinents, tels que le mod??le standard , ne sont pas les th??ories topologiques des champs quantiques; la th??orie quantique du champ effet Hall quantique fractionnaire est une exception notable. Le principal impact de la th??orie du champ quantique topologique axiomatique a ??t?? mis sur les math??matiques, avec d'importantes applications dans th??orie de la repr??sentation, topologie alg??brique et la g??om??trie diff??rentielle .
Trouver les axiomes appropri??s pour la th??orie quantique des champs est encore un probl??me ouvert et difficile en math??matiques. L'un des Prix de Mill??nium de probl??mes-prouver l'existence d'un ??cart de masse dans la th??orie de Yang-Mills-est li?? ?? cette question.
Ph??nom??nes associ??s ?? la th??orie quantique des champs
Dans la partie pr??c??dente de l'article, nous avons d??crit les propri??t??s les plus g??n??rales de th??ories quantiques des champs. Certaines des th??ories quantiques des champs ??tudi??s dans divers domaines de la physique th??orique poss??dent des propri??t??s sp??ciales suppl??mentaires, tels que renormalisabilit??, sym??trie de jauge et la supersym??trie. Ceux-ci sont d??crits dans les sections suivantes.
Renormalisation
T??t dans l'histoire de la th??orie quantique des champs, il a ??t?? constat?? que de nombreux calculs apparemment inoffensifs, tels que le perturbative changement dans l'??nergie d'un ??lectron en raison de la pr??sence du champ ??lectromagn??tique, donnent des r??sultats infinis. Beaucoup de ces probl??mes sont li??s ?? des d??faillances dans ??lectrodynamique classique qui ont ??t?? identifi??s (mais non r??solus) aussi loin que le 19??me si??cle , et elles proviennent essentiellement du fait que la plupart des propri??t??s soi-disant ??intrins??ques?? d'un ??lectron sont li??s au champ ??lectromagn??tique avec lequel il interagit. Pour illustrer cela, le rappel de la discussion pr??c??dente que le hamiltonien d'interaction entre deux champs quantiques, comme le champ d'??lectrons et le champ ??lectromagn??tique, n'a pas besoin de conserver le nombre de particules. Ainsi, m??me si nous commen??ons avec un seul ??lectron et aucun photons, l'??tat quantique va ??voluer rapidement dans une superposition d'??tats qui peuvent inclure un ou plusieurs photons. Par cons??quent, l'??nergie transport??e par ce "single" ??lectron-son auto-??nergie ne est pas simplement la valeur ??nu??, mais comprend ??galement l'??nergie contenue dans un nuage agent de photons. Lorsque cette ??nergie auto est calcul??, on constate que la contribution des ??nergies photons poss??dant arbitrairement ??lev??es (ou, de fa??on ??quivalente, arbitrairement courte longueurs d'onde) conduit ?? une valeur infinie formellement.
La solution ?? ce probl??me, d'abord donn??e par Julian Schwinger, est appel?? renormalisation . L'id??e est d'imposer une " coupure "pour la contribution photonique, par exemple en postulant que les photons ne peuvent pas poss??der des ??nergies d??passant une certaine valeur extr??mement ??lev??e. Toute quantit?? nous souhaitons calculer, tels que l'??nergie reste, est maintenant fini, mais d??pend de la coupure. Nous avons ensuite refondre le r??sultat en termes des quantit??s de physiquement observables comme la masse de l'??lectron observ??e, ?? la place de quantit??s non observables tels que l'??nergie de coupure et de la masse de l'??lectron nu. Le r??sultat final est ind??pendant de tous les d??tails de la proc??dure de coupure, y compris la valeur de l'??nergie de coupure, ?? condition que le processus pertinents se produisent ?? des ??nergies bien en dessous du seuil.
La proc??dure de renormalisation ne fonctionne que pour une certaine classe de th??ories quantiques des champs, appel?? th??ories quantiques des champs renormalisables. Le mod??le standard de la physique des particules est renormalisable, et sont donc ses th??ories de composants ( ??lectrodynamique quantique / th??orie ??lectrofaible et chromodynamique quantique). Selon la th??orie de la groupe de renormalisation, chaque th??orie renormalisable une limite basse ??nergie unique (?? savoir ce qu'on appelle un " th??orie effective sur le terrain ??) pour un large ??ventail de th??ories de haute ??nergie. renormalisable th??ories sont donc ind??pendante de la nature pr??cise des ph??nom??nes de haute ??nergie sous-jacents.
la libert?? de la jauge
Un th??orie de jauge est une th??orie qui admet une sym??trie avec un param??tre local. Par exemple, dans tous les quantique th??orie mondial phase de la fonction d'onde est arbitraire et ne repr??sente pas quelque chose de physique. Par cons??quent, la th??orie est invariante par un changement global de phases (ajout d'une constante ?? la phase de toutes les fonctions d'ondes, partout); c'est un sym??trie globale. En ??lectrodynamique quantique, la th??orie est aussi invariant par un changement local de la phase, ce est - on peut d??caler la phase de tous fonctions d'onde de sorte que le changement peut ??tre diff??rente en tout point l'espace-temps. C'est un sym??trie locale. Cependant, pour qu'un bien d??finie d??riv?? op??rateur existe, il faut introduire une nouvelle domaine, la champ de jauge, qui transforme aussi pour que le changement de variables locales (la phase dans notre exemple) ne pas affecter le d??riv??. En ??lectrodynamique quantique ce champ de jauge est le champ ??lectromagn??tique. La rupture de charge locale de variables est appel?? transformation de jauge.
En th??orie quantique des champs les excitations de champs repr??sentent particules. La particule associ??e ?? des excitations de la champ de jauge est le boson de jauge, qui est le photon dans le cas de ??lectrodynamique quantique.
Le degr??s de libert?? en th??orie quantique des champs sont fluctuations locales des champs. L'existence d'un sym??trie de jauge r??duit le nombre de degr??s de libert??, tout simplement parce que des fluctuations des champs peuvent ??tre transform??s ?? z??ro par ??valuer transformations, de sorte qu'ils sont ??quivalents ?? ne pas avoir les fluctuations du tout, et ils ne ont donc aucune signification physique. Ces fluctuations sont g??n??ralement appel??s "degr??s non-physiques de la libert??" ou des artefacts de jauge; habituellement certains d'entre eux ont une n??gative Norm, ce qui les rend inad??quat pour une th??orie coh??rente. Par conséquent, si une théorie du champ classique a une symétrie de jauge, puis sa version quantifiée (à savoir la théorie quantique des champs correspondant) aura cette symétrie. En d'autres termes, une symétrie de jauge ne ??????peut pas avoir un quantum anomalie. Si une symétrie de jauge est anormale (c.-à-pas gardé dans la théorie quantique) alors la théorie est non-conforme: par exemple, dans l'électrodynamique quantique, il y avait eu une jauge anomalie, cela nécessiterait l'apparition de photons avec longitudinale polarisation et polarisation dans le temps direction, celui-ci ayant un négatif norme, ce qui rend incompatible la théorie; une autre possibilité serait pour ces photons apparaissent uniquement dans les processus intermédiaires, mais pas dans les produits finaux de toute interaction, ce qui rend la théorie non unitaire et encore incompatibles (voir théorème optique).
En g??n??ral, la transformations de jauge d'une théorie consistent plusieurs transformations différentes, qui peuvent ne pas être commutative . Ces transformations sont ainsi décrites par un objet mathématique connu comme un groupe de jauge. infinitésimales transformations de jauge sont le groupe de jauge g??n??rateurs. Par conséquent, le nombre de bosons de jauge est le groupe dimension (nombre de générateurs formant une base).
Tous les interactions fondamentales de la nature sont décrits par th??orie de jauge. Ceux-ci sont:
- Électrodynamique quantique, dontla transformation jauge est un changement local de la phase, de sorte que legroupe de jauge estU (1). Le boson de jauge est lephoton.
- Chromodynamique quantique, dontle groupe est la jauge SU (3). Le bosons de jauge sont huit gluons.
- Le Théorie électrofaible, dont legroupe jauge est
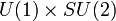 (A produit direct deU (1) etSU (2)).
(A produit direct deU (1) etSU (2)). - Gravity, dont la théorie classique estla relativité générale, admet le principe d'équivalence, qui est une forme de symétrie de jauge.
Supersymétrie
Supersymétrie suppose que chaque fondamentale fermion a une superpartenaire qui est un boson et vice versa. Il a été introduit afin de résoudre le soi-disant problème de hiérarchie, qui est, pour expliquer pourquoi les particules ne sont protégés par aucune symétrie (comme le boson de Higgs) ne reçoivent pas les corrections radiatives à sa masse le conduire aux plus grandes échelles (GUT, Planck ...). Il a été vite réalisé que la supersymétrie a d'autres propriétés intéressantes: sa version calibrée est une extension de la relativité générale ( Supergravity), et il est un ingrédient clé de la cohérence de la théorie des cordes .
La façon supersymmetry protège les hiérarchies est la suivante: étant donné que pour chaque particule il ya un superpartenaire avec la même masse, toute boucle dans une correction radiative est annulée par la boucle correspondant à sa superpartenaire, ce qui rend le fini théorie UV.
Depuis aucun superpartenaires n'a encore été observée, si la supersymétrie existe, il doit être rompu (par un terme douce dite, qui rompt la supersymétrie sans ruiner ses fonctionnalités utiles). Les modèles les plus simples de cette rupture exigent que l'énergie des superpartenaires pas être trop élevé; dans ces cas, la supersymétrie devrait être observé par des expériences à la Grand collisionneur de hadrons.

![\ Left [\ frac {| \ mathbf {p} | ^ 2} {} 2m + V (\ mathbf {r}) \ right] | \ psi (t) \ rang = i \ hbar \ frac {\ partial} { \ partial t} | \ psi (t) \ rang,](../../images/261/26195.png)

![\ Frac {1} {\ sqrt {3}} \ left [| \ phi_1 \ rang | \ phi_2 \ rang | \ phi_2 \ rang + | \ phi_2 \ rang | \ phi_1 \ rang | \ phi_2 \ rang + | \ phi_2 \ rang | \ phi_2 \ rang | \ phi_1 \ rang \ right].](../../images/262/26203.png)
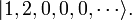

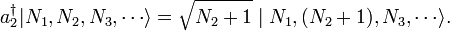
![\ Left [a_i, a_j \ right] = 0 \ quad, \ quad \ left [a_i ^ \ poignard, a_j ^ \ poignard \ right] = 0 \ quad, \ quad \ left [a_i, a_j ^ \ poignard \ right] = \ {ij} delta_,](../../images/262/26211.png)

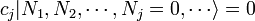

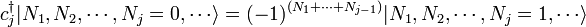
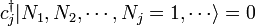


![\ Left [\ phi (\ mathbf {r}), \ phi (\ mathbf {r '}) \ right] = 0 \ quad, \ quad \ left [\ phi ^ \ dagger (\ mathbf {r}), \ phi ^ \ dagger (\ mathbf {r '}) \ right] = 0 \ quad, \ quad \ left [\ phi (\ mathbf {r}), \ phi ^ \ dagger (\ mathbf {r'}) \ right ] = \ delta ^ 3 (\ mathbf {r} - \ mathbf {r '})](../../images/262/26222.png)