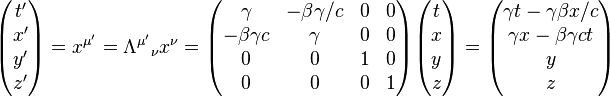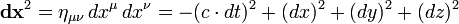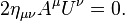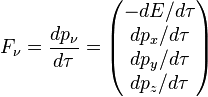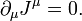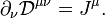Relativit?? restreinte
Contexte des ??coles Wikip??dia
Enfants SOS offrent un chargement complet de la s??lection pour les ??coles pour une utilisation sur les intranets des ??coles. SOS Enfants a regard?? des enfants en Afrique depuis quarante ans. Pouvez-vous aider dans leur travail en Afrique ?
Relativit?? restreinte (SR) (aussi connu comme la th??orie de la relativit?? restreinte ou STR) est le th??orie physique de la mesure dans r??f??rentiels inertiels propos??es en 1905 par Albert Einstein (apr??s contributions consid??rables de Hendrik Lorentz et Henri Poincar??) dans le document " Sur l'??lectrodynamique des corps en mouvement ". Il g??n??ralise Le principe de Galil??e de la relativit?? - que tous les mouvement uniforme est relatif, et qu'il n'y a pas d'??tat absolue et bien d??fini de repos (pas cadres de r??f??rence privil??gi??s) - ?? partir de m??canique ?? tous les lois de la physique, y compris les lois de la m??canique et de l'??lectrodynamique, quels qu'ils soient. En outre, la relativit?? incorpore le principe que la vitesse de la lumi??re est la m??me pour tous inertielle observateurs, ind??pendamment de l'??tat de mouvement de la source.
Cette th??orie a un large ??ventail de cons??quences qui ont ??t?? v??rifi??s exp??rimentalement. Relativit?? restreinte renverse notions newtonienne de l'espace absolu et l'heure en affirmant que le temps et l'espace sont per??us diff??remment par les observateurs dans les diff??rents ??tats de mouvement. Il donne l'??quivalence de la mati??re et de l'??nergie , exprim??e dans la formule d'??quivalence masse-??nergie E = mc 2, o?? c est la vitesse de la lumi??re dans le vide. Les pr??dictions de la relativit?? restreinte en bon accord avec la m??canique newtonienne dans leur domaine d'application commune, en particulier dans des exp??riences dans lesquelles toutes les vitesses sont faibles par rapport ?? la vitesse de la lumi??re.
La th??orie est appel??e ??sp??cial?? car il applique la principe de relativit?? seulement r??f??rentiels inertiels. Einstein a d??velopp?? la relativit?? g??n??rale d'appliquer le principe g??n??ral, ce est, ?? ne importe quel cadre, et que la th??orie comprend les effets de la gravit?? . Strictement, la relativit?? restreinte ne peut pas ??tre appliqu??e dans l'acc??l??ration de cadres ou dans les champs gravitationnels.
La relativit?? sp??ciale r??v??le que c ne est pas seulement la vitesse d'un certain ph??nom??ne, ?? savoir la propagation du rayonnement ??lectromagn??tique (la lumi??re), mais plut??t une caract??ristique fondamentale de l'espace et le temps moyen sont unifi??s comme l'espace-temps. Une cons??quence de ceci est qu'il est impossible ?? une particule qui a une masse ?? acc??l??rer ?? la vitesse de la lumi??re.
Pour l'histoire et de la motivation, consultez l'article: Histoire de la relativit?? restreinte
Postulats
Dans ses notes autobiographiques publi??s en Novembre 1949 Einstein a d??crit comment il ??tait arriv?? aux deux postulats fondamentaux sur lesquels il repose la th??orie de la relativit??. Apr??s avoir d??crit en d??tail l'??tat des deux m??caniciens et l'??lectrodynamique au d??but du 20e si??cle, il a ??crit
"R??flexions de ce type fait clair pour moi il ya aussi longtemps que peu apr??s 1900, ce est ?? dire, peu de temps apr??s le travail de pionnier de Planck, que ni les m??caniciens ni l'??lectrodynamique pourrait (sauf dans les cas de limitation) affirment validit?? exacte. Peu ?? peu, je d??sesp??rais de la possibilit?? de d??couvrir les v??ritables lois au moyen d'efforts constructifs bas??s sur des faits connus. Le plus long et plus d??sesp??r??ment Je ai essay??, plus je suis arriv?? ?? la conviction que seule la d??couverte d'un principe formel universelle pourrait nous conduire ?? des r??sultats assur??s ... Comment, puis , un tel principe universel pourrait ??tre trouv??? "
Il discerna deux propositions fondamentales qui semblaient ??tre le plus assur??, ind??pendamment de la validit?? exacte soit des lois (puis) connus de la m??canique ou de l'??lectrodynamique. Ces propositions ??taient (1) la constance de la vitesse de la lumi??re, et (2) l'ind??pendance des lois physiques (en particulier la constance de la vitesse de la lumi??re) du choix du syst??me inertiel. Dans sa pr??sentation initiale de la relativit?? restreinte en 1905 il a exprim?? ces postulats que:
- Le principe de la relativit?? - Les lois par lesquelles les Etats de syst??mes physiques subissant des modifications ne sont pas affect??s, si ces changements d'??tat ??tre nomm?? l'un ou l'autre des deux syst??mes de coordonn??es inertielles en mouvement de translation uniforme.
- Le principe de Invariant Lumi??re Vitesse - lumi??re dans le vide se propage avec la vitesse c (une constante fixe) en termes de ne importe quel syst??me de coordonn??es inertielles, ind??pendamment de l'??tat de mouvement de la source lumineuse.
Il convient de noter que la d??rivation de la relativit?? restreinte ne d??pend pas seulement sur ces deux postulats explicites, mais aussi sur plusieurs hypoth??ses tacites (qui sont faites dans presque toutes les th??ories de la physique), y compris le isotropie et homog??n??it?? de l'espace et l'ind??pendance de piges et horloges de leur histoire pass??e.
Suite ?? la pr??sentation originale d'Einstein de la relativit?? restreinte en 1905, de nombreux ensembles diff??rents de postulats ont ??t?? propos??es dans divers d??rivations alternatives. Toutefois, l'ensemble le plus commun de postulats reste ceux employ??s par Einstein dans son article original. Ces postulats se r??f??rent ?? la base axiomatique de la Transformation de Lorentz, qui est le noyau essentiel de la relativit?? restreinte. Dans tous les papiers d'Einstein dans laquelle il a pr??sent?? les d??rivations de la transformation de Lorentz, il repose sur ces deux principes.
En plus des documents mentionn??s ci-dessus qui donnent d??rivations de la transformation de Lorentz et d??crivent les fondements de la relativit?? sp??ciale-Einstein a ??galement ??crit au moins quatre documents donnant des arguments heuristiques pour l'??quivalence (et transmutabilit??) de la masse et de l'??nergie. (Il convient de noter que cette ??quivalence ne d??coule pas des pr??misses fondamentales de la relativit?? restreinte. Le premier d'entre eux ??tait "L'inertie d'un corps d??pend de son contenu ??nerg??tique?" En 1905. Dans ce domaine et chacun de ses trois documents ult??rieurs ?? ce sujet, Einstein augment?? les deux principes fondamentaux en postulant les relations impliquant ??lan et l'??nergie des ondes ??lectromagn??tiques sous-entendus par les ??quations de Maxwell (la prise en charge de ce qui, bien s??r, implique entre autres l'hypoth??se de la constance de la vitesse de la lumi??re). Il a reconnu dans son document de l'enqu??te 1907 sur la relativit?? sp??ciale qu'il ??tait probl??matique de se appuyer sur les ??quations de Maxwell pour l'heuristique argument de masse-??nergie, et ce est pourquoi il a toujours fond?? la d??rivation de l'invariance de Lorentz (le noyau essentiel de la relativit?? restreinte) uniquement sur le deux principes de base de la relativit?? et invariance vitesse de la lumi??re. Il a ??crit
"L'id??e fondamentale de la th??orie de la relativit?? restreinte est la suivante: La hypoth??ses relativit?? et l'invariance de la vitesse de la lumi??re sont compatibles si les relations d'un type nouveau (" de transformation de Lorentz ??) sont postul??s pour la conversion de coordonn??es et heures des ??v??nements ... L'universel principe de la th??orie de la relativit?? restreinte est contenue dans le postulat:. Les lois de la physique sont invariantes par rapport aux transformations de Lorentz (pour la transition d'un syst??me inertiel ?? tout autre syst??me d'inertie choisi arbitrairement) Ce est un principe de limitation des lois naturelles. .. "
Ainsi de nombreux traitements modernes de base de la relativit?? restreinte sur le postulat universel unique de covariance de Lorentz, ou, de fa??on ??quivalente, sur le postulat unique de l'espace-temps de Minkowski.
Cons??quences
Einstein a dit que toutes les cons??quences de la relativit?? restreinte peuvent ??tre tir??es de l'examen de la Transformations de Lorentz.
Ces transformations, et la relativit?? sp??ciale par cons??quent, conduire ?? des pr??dictions diff??rentes physiques que la m??canique newtonienne quand vitesses relatives deviennent comparables ?? la vitesse de la lumi??re. La vitesse de la lumi??re est tellement plus grand que l'homme de tout ce que rencontrent certains des effets pr??vus par la relativit?? sont d'abord contre-intuitif:
- Dilatation du temps - le temps ??coul?? entre deux ??v??nements ne est pas invariant d'un observateur ?? l'autre, mais d??pend des vitesses relatives des cadres de r??f??rence des observateurs (par exemple, le double paradoxe qui concerne un jumeau qui se envole dans un vaisseau spatial voyageant pr??s de la vitesse de la lumi??re et retourne pour d??couvrir que son fr??re jumeau a vieilli beaucoup plus).
- Relativit?? de la simultan??it?? - deux ??v??nements qui se d??roulent dans deux endroits diff??rents qui se produisent simultan??ment un observateur, peut se produire ?? diff??rents moments pour un autre observateur (manque de simultan??it?? absolue).
- Contraction de Lorentz - les dimensions (par exemple, la longueur) d'un objet tel que mesur?? par un observateur peut ??tre plus petite que les r??sultats des mesures du m??me objet faites par un autre observateur (par exemple, le ladder paradoxe implique une longue ??chelle voyageant pr??s de la vitesse de la lumi??re et ??tant contenue dans un garage plus petit).
- Composition des vitesses - vitesses (et vitesses) ne simplement ??ajouter??, par exemple si une roquette se d??place ?? ⅔ la vitesse de la lumi??re par rapport ?? un observateur, et la fus??e tire un missile sur ⅔ de la vitesse de la lumi??re par rapport ?? la fus??e, missile ne d??passe pas la vitesse de la lumi??re par rapport ?? l'observateur. (Dans cet exemple, l'observateur verrait le Voyage de missiles avec une vitesse de 12/13 de la vitesse de la lumi??re.)
- Inertie et dynamique - que la vitesse d'un objet se approche de la vitesse de la lumi??re du point de vue d'un observateur, sa masse semble augmenter ce qui rend de plus en plus difficile pour acc??l??rer de l'int??rieur du cadre de r??f??rence de l'observateur.
- ??quivalence de la masse et de l'??nergie , E = mc 2 - Le contenu ??nerg??tique d'un objet au repos de masse m est ??gal
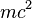 . Conservation de l'??nergie implique que dans ne importe quelle r??action une diminution de la somme des masses de particules doit ??tre accompagn??e d'une augmentation de l'??nergie cin??tique des particules apr??s la r??action. De m??me, la masse d'un objet peut ??tre augment??e en prenant dans les ??nergies cin??tiques.
. Conservation de l'??nergie implique que dans ne importe quelle r??action une diminution de la somme des masses de particules doit ??tre accompagn??e d'une augmentation de l'??nergie cin??tique des particules apr??s la r??action. De m??me, la masse d'un objet peut ??tre augment??e en prenant dans les ??nergies cin??tiques.
Simultan??it??

De la premi??re ??quation de la transformation de Lorentz en termes de diff??rences de coordonn??es
il est clair que deux ??v??nements qui sont simultan??ment dans un cadre S (satisfaisant  ), Ne sont pas n??cessairement simultan??es dans un autre inertiel S ??(satisfaisant
), Ne sont pas n??cessairement simultan??es dans un autre inertiel S ??(satisfaisant  ). Seulement si ces ??v??nements sont colocal dans un cadre S (satisfaisant
). Seulement si ces ??v??nements sont colocal dans un cadre S (satisfaisant 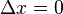 ), Seront-ils simultan??e dans un autre cadre S '.
), Seront-ils simultan??e dans un autre cadre S '.
Dilatation du temps et de la contraction des longueurs
R??daction la transformation de Lorentz et son inverse en termes de coordonner les diff??rences que nous obtenons
et
Supposons que nous avons une horloge au repos dans le syst??me sans appr??t S. Deux tiques cons??cutives de cette horloge sont ensuite caract??ris??s par 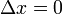 . Si nous voulons conna??tre la relation entre les temps entre ces tiques tels que mesur??s dans les deux syst??mes, nous pouvons utiliser la premi??re ??quation et de trouver:
. Si nous voulons conna??tre la relation entre les temps entre ces tiques tels que mesur??s dans les deux syst??mes, nous pouvons utiliser la premi??re ??quation et de trouver:
 pour les ??v??nements r??pondant
pour les ??v??nements r??pondant 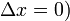
Cela montre que le temps  entre les deux tiques comme on le voit dans le 'mouvement' trame S 'est plus grand que le temps
entre les deux tiques comme on le voit dans le 'mouvement' trame S 'est plus grand que le temps  entre ces tiques telle que mesur??e dans le cadre de l'horloge de repos. Ce ph??nom??ne est appel?? la dilatation du temps.
entre ces tiques telle que mesur??e dans le cadre de l'horloge de repos. Ce ph??nom??ne est appel?? la dilatation du temps.
De m??me, supposons que nous avons une pige au repos dans le syst??me sans appr??t. Dans ce syst??me, la longueur de cette tige se ??crit 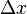 . Si nous voulons trouver la longueur de cette tige, mesur??e dans le 'mouvement' syst??me S ', nous devons nous assurer de mesurer les distances
. Si nous voulons trouver la longueur de cette tige, mesur??e dans le 'mouvement' syst??me S ', nous devons nous assurer de mesurer les distances  pour les points de la tige en m??me temps dans la trame S appr??t?? d'extr??mit??. En d'autres termes, la mesure est caract??ris?? par
pour les points de la tige en m??me temps dans la trame S appr??t?? d'extr??mit??. En d'autres termes, la mesure est caract??ris?? par  , Que nous pouvons combiner avec la quatri??me ??quation pour trouver la relation entre les longueurs
, Que nous pouvons combiner avec la quatri??me ??quation pour trouver la relation entre les longueurs 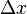 et
et  :
:
 pour les ??v??nements r??pondant
pour les ??v??nements r??pondant 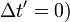
Cela montre que la longueur  de la tige, telle que mesur??e dans le "d??placement" cadre S 'est plus courte que la longueur
de la tige, telle que mesur??e dans le "d??placement" cadre S 'est plus courte que la longueur 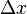 dans son propre cadre de repos. Ce ph??nom??ne est appel?? longueur contraction ou contraction de Lorentz.
dans son propre cadre de repos. Ce ph??nom??ne est appel?? longueur contraction ou contraction de Lorentz.
Ces effets ne sont pas de simples apparences; ils sont explicitement li??s ?? notre fa??on de mesurer des intervalles de temps entre les ??v??nements qui se produisent au m??me endroit dans un syst??me donn?? de coordonn??es (appel?? co-??v??nements "locaux"). Ces intervalles de temps seront diff??rentes dans un autre syst??me de coordonn??es se d??pla??ant par rapport ?? la premi??re, ?? moins que les ??v??nements sont aussi simultan??ment. De m??me, ces effets se rapportent ??galement ?? nos distances mesur??es entre les ??v??nements s??par??s mais simultan??s dans un syst??me donn?? de coordonn??es de choix. Si ces ??v??nements ne sont pas co-local, mais sont s??par??es par la distance (espace), ils ne se produisent ?? la m??me distance spatiale l'une de l'autre lorsqu'il est vu d'un autre syst??me de coordonn??es se d??pla??ant.
Voir aussi le paradoxe des jumeaux.
Causalit?? et l'interdiction de mouvement vite que la lumi??re

Dans le sch??ma 2 est l'intervalle AB "temps-like??, ?? savoir, il existe un cadre de r??f??rence, auquel cas A et B ??v??nement se produisent au m??me endroit dans l'espace, s??par?? seulement par se produisant ?? des moments diff??rents. Si A pr??c??de B dans ce cadre, alors A pr??c??de B dans tous les cadres. Il est th??oriquement possible pour la mati??re (ou informations) pour aller de A ?? B, alors il peut y avoir un lien de causalit?? (avec A la cause et l'effet B).
L'AC intervalle dans le sch??ma est ??comme l'espace-'; ce est ?? dire, il ya un cadre de r??f??rence auquel cas A et C ??v??nement se produisent simultan??ment, s??par??s seulement dans l'espace. Cependant, il ya aussi des cadres dans lesquels A pr??c??de C (comme indiqu??) et ch??ssis en C qui pr??c??de A. Se il ??tait possible pour une relation et de cause ?? effet entre les ??v??nements d'exister A et C, puis paradoxes de la causalit?? en r??sulteraient. Par exemple, si A est la cause et l'effet C, alors il n'y aurait cadres de r??f??rence dans lequel l'effet pr??c??d?? la cause. Bien que ce qui en soi ne donnera pas lieu ?? un paradoxe, on peut montrer que plus rapide que des signaux lumineux peuvent ??tre renvoy??s dans le pass?? de l'un. Un paradoxe de causalit?? peut alors ??tre construit en envoyant le signal si et seulement si aucun signal n'a ??t?? re??u auparavant.
Par cons??quent, l'une des cons??quences de la relativit?? restreinte est que (en supposant causalit?? doit ??tre pr??serv??), aucune information ou objet mat??riel peut voyager vite que la lumi??re. D'autre part, la situation logique est pas aussi claire dans le cas de la relativit?? g??n??rale, il est donc une question ouverte se il existe une principe fondamental qui pr??serve la causalit?? (et donc emp??che le mouvement plus rapide que la lumi??re) en relativit?? g??n??rale.
M??me sans consid??rations de causalit??, il ya d'autres bonnes raisons pourquoi plus vite que la lumi??re Voyage est interdit par la relativit?? restreinte. Par exemple, si une force constante est appliqu??e ?? un objet pour un montant illimit?? de fois, puis en int??grant F = dp / dt donne un ??lan qui pousse sans borne, mais ce est tout simplement parce que  tend vers l'infini comme v approche c. Pour un observateur qui ne est pas acc??l??r??, il semble que l'inertie de l'objet augmente, de mani??re ?? produire une acc??l??ration plus faible en r??ponse ?? la m??me valeur. Ce comportement est en fait observ??e dans des acc??l??rateurs de particules.
tend vers l'infini comme v approche c. Pour un observateur qui ne est pas acc??l??r??, il semble que l'inertie de l'objet augmente, de mani??re ?? produire une acc??l??ration plus faible en r??ponse ?? la m??me valeur. Ce comportement est en fait observ??e dans des acc??l??rateurs de particules.
Voir aussi le Tachyonique Antitelephone.
Composition de vitesses
Si l'observateur S voit un objet se d??pla??ant le long de l'axe x ?? la vitesse w, puis l'observateur dans le syst??me S ', un cadre de r??f??rence se d??pla??ant ?? la vitesse v dans la direction x par rapport ?? S, verront l'objet en mouvement avec une vitesse w 'o??
Cette ??quation peut ??tre d??riv??e ?? partir des transformations spatiales et temporelles ci-dessus. Notez que si l'objet se d??pla??ait ?? la vitesse de la lumi??re dans le syst??me de S (c.-??-  ), Alors il serait ??galement d??place ?? la vitesse de la lumi??re dans le syst??me S '. En outre, si les deux w et v sont de petite taille par rapport ?? la vitesse de la lumi??re, nous r??cup??rons la transformation galil??enne intuitive de vitesses:
), Alors il serait ??galement d??place ?? la vitesse de la lumi??re dans le syst??me S '. En outre, si les deux w et v sont de petite taille par rapport ?? la vitesse de la lumi??re, nous r??cup??rons la transformation galil??enne intuitive de vitesses: 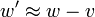 .
.
Messe, l'??lan et l'??nergie
En plus de modifier les notions d'espace et de temps, les forces de la relativit?? restreinte une ?? reconsid??rer les notions de masse , dynamique et l'??nergie , qui sont tous des constructions importantes de la m??canique newtonienne . Pr??sentations sp??ciales de la relativit??, en fait, que ces concepts sont tous les diff??rents aspects de la m??me quantit?? physique de la m??me fa??on qu'il montre l'espace et de temps pour ??tre interreli??s.
Il ya un couple de (??quivalentes) fa??ons de d??finir ??lan et l'??nergie dans la RS. On utilise la m??thode lois de conservation. Si ces lois doivent rester valables dans SR ils doivent ??tre vrai dans chaque cadre de r??f??rence possible. Toutefois, si l'on fait quelques simples pens?? exp??riences utilisant les d??finitions newtonienne de mouvement et d'??nergie que l'on voit que ces quantit??s ne sont pas conserv??es dans SR. On peut sauver l'id??e de la conservation en faisant quelques petites modifications aux d??finitions pour tenir compte des vitesses relativistes. Ce sont ces nouvelles d??finitions qui sont prises comme les bons de mouvement et d'??nergie dans la RS.
Compte tenu de l'objet de invariant masse m se d??pla??ant ?? la vitesse v l'??nergie et l'??lan sont donn??s (et m??me d??finie) par
o?? γ (le Facteur de Lorentz) est donn??e par
o??  est le rapport entre la vitesse et la vitesse de la lumi??re. Le terme γ se produit fr??quemment dans la relativit??, et provient de la ??quations de transformation de Lorentz.
est le rapport entre la vitesse et la vitesse de la lumi??re. Le terme γ se produit fr??quemment dans la relativit??, et provient de la ??quations de transformation de Lorentz.
L'??nergie et l'??lan relativiste peuvent ??tre li??s par la formule
qui est appel?? l'??quation ??nergie-impulsion relativiste. Il est int??ressant de noter que tandis que l'??nergie 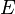 et l'??lan
et l'??lan 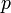 d??pendent observateur (varier d'une image ??) la quantit??
d??pendent observateur (varier d'une image ??) la quantit??  est observateur ind??pendant.
est observateur ind??pendant.
Pour des vitesses beaucoup plus faibles que celles de la lumi??re, γ peuvent ??tre estim??s ?? l'aide d'un d??veloppement en s??rie de Taylor et on constate que
Sauf le premier terme de l'expression de l'??nergie (voir ci-dessous), ces formules se accordent exactement avec les d??finitions normalis??es des newtonienne ??nergie cin??tique et de l'??lan. Ce est comme il se doit, par la relativit?? restreinte doit correspondre ?? la m??canique newtonienne ?? basses vitesses.
En regardant les formules ci-dessus pour l'??nergie, on voit que quand un objet est au repos (v = 0 et γ = 1) il ya une ??nergie non nulle restant:
Cette ??nergie est appel??e ??nergie reste. L'??nergie de repos ne est pas incompatible avec la th??orie newtonienne parce que ce est une constante et, autant que l'??nergie cin??tique est concern??, il est seulement des diff??rences de l'??nergie qui sont significatives.
Prenant cette formule ?? leur valeur nominale, nous voyons que dans la relativit??, la masse est simplement une autre forme d'??nergie. En 1927, Einstein a fait remarquer ?? propos de la relativit?? restreinte:
Sous cette masse de la th??orie ne est pas une grandeur immuable, mais une amplitude d??pend (et, en fait, identique ??) la quantit?? d'??nergie.
Cette formule devient important lorsque l'on mesure les masses des diff??rents noyaux atomiques. En regardant la diff??rence dans les masses, on peut pr??dire quels noyaux ont suppl??mentaire stock??e ??nergie qui peut ??tre lib??r?? par r??actions nucl??aires, fournissant des informations importantes qui ??tait utile dans le d??veloppement de l'??nergie nucl??aire et, par cons??quent, la bombe nucl??aire . Les cons??quences de cette formule sur la vie du 20e si??cle ont fait l'une des plus c??l??bres ??quations les de toute la science.
Masse relativiste
Cours de physique d'introduction et quelques anciens manuels sur la relativit?? restreinte d??finissent parfois un masse relativiste qui augmente lorsque la vitesse d'un corps augmente. Selon l'interpr??tation g??om??trique de la relativit?? restreinte, ce qui est souvent obsol??te et le terme ??masse?? est r??serv?? pour signifier masse invariante et est donc ind??pendant de la trame d'inertie, ce est-invariant.
En utilisant la d??finition de masse relativiste, la masse d'un objet peut varier en fonction de r??f??rentiel inertiel de l'observateur de la m??me mani??re que d'autres propri??t??s telles que sa longueur peuvent le faire. D??finition d'une telle quantit?? peut parfois ??tre utile en ce faisant simplifie le calcul en le limitant ?? une image sp??cifique. Par exemple, consid??rons un corps avec une masse invariante m se d??pla??ant ?? une certaine vitesse relative au syst??me de r??f??rence d'un observateur. Cet observateur d??finit la masse relativiste de ce corps comme:
"Masse relativiste" ne doit pas ??tre confondu avec les d??finitions et "longitudinaux" "masse transversale?? qui ont ??t?? utilis??s dans les ann??es 1900 et qui ont ??t?? bas??es sur une application incoh??rente des lois de Newton: ceux utilis??s F = ma pour une masse variable tandis relativiste masse correspond ?? masse dynamique de Newton dans lequel
et
 .
.
Notez ??galement que le corps n'a pas effectivement devenir plus massif dans son cadre propre, puisque la masse relativiste est seulement diff??rent pour un observateur dans un cadre diff??rent. La seule masse qui est b??ti ind??pendant est le masse invariante. Lorsque vous utilisez la masse relativiste, le cadre de r??f??rence applicable devrait ??tre sp??cifi?? si ce ne est d??j?? ??vidente ou implicite. Il va ??galement sans dire que l'augmentation de la masse relativiste ne vient pas d'un nombre accru d'atomes dans l'objet. Au lieu de cela, la masse relativiste de chaque atome et subatomique particules a augment??.
manuels de physique utilisent parfois la masse relativiste car elle permet aux ??l??ves d'utiliser leurs connaissances de la physique newtonienne d'acqu??rir une certaine compr??hension intuitive de la relativit?? dans leur cadre de choix (g??n??ralement leur propre!). "Masse relativiste" est ??galement compatible avec les concepts " dilatation du temps "et" la contraction des longueurs ".
Force
La d??finition classique de l'ordinaire force f est donn??e par la deuxi??me loi de Newton dans sa forme originale:
et ce est valable dans la relativit??.
De nombreux manuels modernes r????crire la deuxi??me loi de Newton
Cette forme ne est pas valable dans la relativit?? ou dans d'autres situations o?? la masse relativiste M est variable.
Cette formule peut ??tre remplac?? dans le cas relativiste par
Comme on le voit ?? partir de l'??quation, vecteurs de force et d'acc??l??ration ordinaires ne sont pas n??cessairement parall??les dans la relativit??.
Cependant l'expression de quatre vecteur relatif quatre vigueur  ?? invariant masse m et quatre acc??l??ration
?? invariant masse m et quatre acc??l??ration 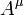 restaure la m??me forme d'??quation
restaure la m??me forme d'??quation
La g??om??trie de l'espace-temps
SR utilise un espace de Minkowski quatre dimensions 'flat', qui est un exemple de l'espace-temps. Cet espace, cependant, est tr??s similaire ?? la norme dimensionnelle 3 espace euclidien , et heureusement, par le fait, tr??s facile ?? travailler avec.
Le ??cart de distance (ds) en espace 3D cart??sien est d??fini comme:
o?? 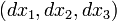 sont les diff??rences des trois dimensions spatiales. Dans la g??om??trie de la relativit??, une quatri??me dimension est ajout??e, d??riv??e de l'heure, de sorte que l'??quation de la diff??rence de distance devient:
sont les diff??rences des trois dimensions spatiales. Dans la g??om??trie de la relativit??, une quatri??me dimension est ajout??e, d??riv??e de l'heure, de sorte que l'??quation de la diff??rence de distance devient:
Si nous voulions prendre le temps de coordonner ressembler l'espace coordonn??es, nous pourrions traiter temps que imaginaire: x 4 = TIC. Dans ce cas, l'??quation ci-dessus devient sym??trique:
Ceci sugg??re ce est en fait un aper??u th??orique profonde car il montre que la relativit?? restreinte est tout simplement un sym??trie de rotation de notre l'espace-temps, tr??s semblable ?? sym??trie de rotation de l'espace euclidien . Tout comme l'espace euclidien utilise un M??trique euclidienne, donc l'espace-temps utilise un M??trique de Minkowski. Fondamentalement, SR peut ??tre formul??e en termes de l'invariance de l'intervalle espace-temps (entre deux ??v??nements) comme on le voit ?? partir de ne importe quel cadre de r??f??rence inertiel. Toutes les ??quations et les effets de la relativit?? restreinte peuvent ??tre tir??s de cette sym??trie de rotation (la Groupe de Poincar??) de l'espace-temps de Minkowski. Selon Misner (1971 ?? 2.3), en fin de compte la meilleure compr??hension de la relativit?? restreinte et g??n??rale viendra de l'??tude de la m??trique de Minkowski (d??crit ci-dessous) plut??t que d'un "d??guis??e" m??trique euclidienne l'utilisation des TIC comme le temps de coordonner.
Si nous r??duisons les dimensions spatiales ?? 2, de sorte que nous pouvons repr??senter la physique dans un espace 3-D
Nous voyons que le nul g??od??siques se trouvent le long d'un double c??ne:
d??fini par l'??quation
ou
Ce est l'??quation d'un cercle avec r = c ?? dt. Si nous ??tendons ce ?? trois dimensions spatiales, les g??od??siques nulles sont le c??ne 4 dimensions:
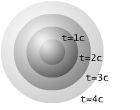
Cette double c??ne nulle repr??sente la "ligne de mire" d'un point dans l'espace. Ce est, quand on regarde les ??toiles et dire "La lumi??re de cette ??toile que je re??ois est de X ans??, nous recherchons dans cette ligne de mire: une g??od??sique nulle. Nous sommes ?? la recherche lors d'un ??v??nement 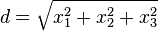 m??tres et d / c secondes dans le pass??. Pour cette raison, l'hypoth??se nulle double c??ne est ??galement connu comme le "c??ne de lumi??re '. (Le point en bas ?? gauche de l'image ci-dessous repr??sente l'??toile, l'origine repr??sente l'observateur, et la ligne repr??sente la g??od??sique "ligne de mire" null.)
m??tres et d / c secondes dans le pass??. Pour cette raison, l'hypoth??se nulle double c??ne est ??galement connu comme le "c??ne de lumi??re '. (Le point en bas ?? gauche de l'image ci-dessous repr??sente l'??toile, l'origine repr??sente l'observateur, et la ligne repr??sente la g??od??sique "ligne de mire" null.)
Le c??ne dans la r??gion -t est l'information que le point est ??re??oit??, tandis que le c??ne dans la section + t est l'information que le point est ??envoie??.
La g??om??trie de l'espace de Minkowski peut ??tre repr??sent?? ?? l'aide Diagrammes de Minkowski, qui sont ??galement utiles dans la compr??hension de la plupart des exp??riences de pens??e dans la relativit?? sp??ciale.
Physique dans l'espace-temps
Ici, nous voyons comment ??crire les ??quations de la relativit?? sp??ciale dans un manifestement Lorentz covariante forme. La position d'un ??v??nement dans l'espace-temps est donn??e par un contravariant quatre vecteur dont les composantes sont:
C'est,  et
et 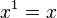 et
et 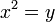 et
et 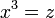 . Exposants sont des indices contravariants dans cette section plut??t que les exposants, sauf quand ils indiquent un carr??. Les indices sont indices covariants qui vont ??galement de z??ro ?? trois comme le gradient de l'espace-temps d'un φ de domaine:
. Exposants sont des indices contravariants dans cette section plut??t que les exposants, sauf quand ils indiquent un carr??. Les indices sont indices covariants qui vont ??galement de z??ro ?? trois comme le gradient de l'espace-temps d'un φ de domaine:
Metric et les transformations de coordonn??es
Ayant reconnu le caract??re ?? quatre dimensions de l'espace-temps, nous sommes amen??s ?? utiliser le m??trique de Minkowski, η, donn??e dans les composants (valable dans tous les r??f??rentiel inertiel) que:
Son r??ciproque est la suivante:
Ensuite, nous reconnaissons que les transformations de coordonn??es entre les cadres de r??f??rence inertiels sont donn??s par les Transformation de Lorentz tenseur Λ. Pour le cas particulier du mouvement le long de la axe x, nous avons:
qui est tout simplement la matrice d'un coup de pouce (comme une rotation) entre les coordonn??es x et t. O?? μ 'indique la ligne et ν indique la colonne. En outre, β et γ sont d??finis comme suit:
Plus g??n??ralement, une transformation d'un r??f??rentiel inertiel (ignorant traductions pour plus de simplicit??) ?? un autre doit satisfaire:
o?? il ya une sommation implicite de  et
et  de 0 ?? 3 sur le c??t?? droit conform??ment ?? la Einstein convention de sommation. Le Groupe de Poincar?? est le groupe le plus g??n??ral des transformations qui pr??serve la M??trique de Minkowski et ce est la sym??trie physique sous-jacente la relativit?? restreinte.
de 0 ?? 3 sur le c??t?? droit conform??ment ?? la Einstein convention de sommation. Le Groupe de Poincar?? est le groupe le plus g??n??ral des transformations qui pr??serve la M??trique de Minkowski et ce est la sym??trie physique sous-jacente la relativit?? restreinte.
Toutes les quantit??s physiques ad??quates sont fournies par tenseurs. Donc, pour transformer d'une image ?? l'autre, nous utilisons le bien-connue la loi de transformation des tenseurs
O??  est la matrice inverse de
est la matrice inverse de 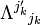 .
.
Pour voir comment cela est utile, nous transformons la position d'un ??v??nement ?? partir d'un syst??me de coordonn??es sans appr??t S ?? un syst??me amorc??e S ', nous calculons
qui est la transformation de Lorentz donn?? ci-dessus. Tous les tenseurs transforment par la m??me r??gle.
La longueur carr?? de l'??cart de la position quatre vecteur  construit en utilisant
construit en utilisant
est un invariant. Signifie ??tre invariant qu'il prend la m??me valeur dans tous les r??f??rentiels inertiels, parce que ce est un scalaire (0 rang tenseur), et donc pas Λ appara??t dans sa transformation trivial. Notez que lorsque le ??l??ment de ligne 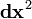 est n??gatif
est n??gatif 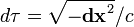 est l'??cart de bon moment, alors que lorsque
est l'??cart de bon moment, alors que lorsque 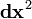 est positif,
est positif,  est le diff??rentiel de bonne distance.
est le diff??rentiel de bonne distance.
La valeur principale d'exprimer les ??quations de la physique sous une forme de tenseur, ce est qu'ils sont alors manifestement invariant sous le groupe de Poincar??, de sorte que nous ne avons pas ?? faire un calcul sp??cial et fastidieux de v??rifier ce fait. Aussi dans la construction de ces ??quations nous constatons souvent que les ??quations que l'on croyait sans rapport sont, en fait, ??troitement li??s faisant partie de la m??me ??quation de tenseur.
Vitesse et acc??l??ration dans 4D
Reconnaissant autres grandeurs physiques comme tenseurs simplifie aussi leurs lois de transformation. Notons d'abord que le la vitesse de quatre vecteur U μ est donn??e par
Reconnaissant cela, nous pouvons tourner la loi regardant maladroite sur la composition des vitesses dans une simple d??claration de transformer la vitesse de quatre vecteur d'une particule d'une image ?? l'autre U μ a ??galement une forme invariante.:
Donc, tous les quatre vecteurs vitesse ont une magnitude de c. Ce est une expression du fait qu'il n'y a pas une telle chose comme ??tant ?? coordonner repos dans la relativit??: au moins, vous ??tes toujours en mouvement vers l'avant ?? travers le temps. Le acc??l??ration 4-vecteur est donn?? par  . Compte tenu de cela, diff??renciant l'??quation ci-dessus par τ produit
. Compte tenu de cela, diff??renciant l'??quation ci-dessus par τ produit
Donc, dans la relativit??, l'acc??l??ration quatre vecteur et la vitesse de quatre-vecteur sont orthogonales.
Momentum dans 4D
L'??lan et l'??nergie se combinent dans un 4-vecteur covariant:
o?? m est le masse invariante.
L'ampleur de l'invariant dynamique 4-vecteur est:
Nous pouvons travailler sur ce que cet invariant est d'abord en faisant valoir que, puisque ce est un scalaire, il ne est pas question que nous calculons le rep??re, puis en transformant ?? un cadre o?? l'impulsion totale est ??gale ?? z??ro.
Nous voyons que l'??nergie reste est un invariant ind??pendant. Une ??nergie de repos peut ??tre calcul??e m??me pour les particules et les syst??mes en mouvement, en traduisant ?? un cadre dans lequel l'??lan est z??ro.
L'??nergie reste est li?? ?? la masse selon le c??l??bre ??quation discut?? ci-dessus:
A noter que la masse des syst??mes de mesure en leur centre de trame d'impulsion (quantit?? de mouvement totale o?? est ??gal ?? z??ro) est donn??e par l'??nergie totale du syst??me dans ce cadre. Il peut ne pas ??tre ??gale ?? la somme des masses individuelles du syst??me de mesure dans d'autres cadres.
Vigueur en 4D
Pour utiliser la troisième loi du mouvement de Newton , les deux forces doivent être définies comme le taux de variation de l'élan par rapport à la même période de coordonnées. Autrement dit, il nécessite la force 3D défini ci-dessus. Malheureusement, il n'y a pas tenseur en 4D qui contient les composants du vecteur de force 3D parmi ses composants.
Si une particule ne se déplace pas au c , on peut transformer la force 3D à partir de la trame de référence de co-mouvement de la particule dans le cadre de référence de l'observateur. Cela donne un vecteur 4 appelé quatre vigueur. Il est le taux de variation de l'élan d'énergie au-dessus de quatre-vecteur par rapport au temps approprié. La version covariante de quatre-vigueur est:
o?? 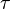 est le bon moment.
est le bon moment.
Dans le cadre reste de l'objet, le composant de temps de quatre vigueur est nulle à moins que le " masse invariante "de l'objet est en train de changer dans ce cas, il est le négatif de ce taux de changement fois c 2 . En général, cependant, les quatre composants de la vigueur ne sont pas égaux pour les trois composantes de la force, car la force de trois est définie par le taux de variation de quantité de mouvement par rapport à coordonner temps, soit  pendant que la force de quatre est définie par le taux de variation de l'élan par rapport au temps approprié, c.-à-
pendant que la force de quatre est définie par le taux de variation de l'élan par rapport au temps approprié, c.-à- 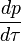 .
.
Dans un milieu continu, le 3D densité de la force se combine avec la densité de puissance pour former un 4-vecteur covariant. La partie spatiale est le résultat de la division de la force sur une petite cellule (en l'espace de 3) par le volume de cette cellule. Le composant de temps est le négatif de la puissance transférée à cette cellule divisée par le volume de la cellule. Il sera utilisé ci-dessous dans la section sur l'électromagnétisme.
Relativité et électromagnétisme d'unification
Etude théorique dans l'électromagnétisme classique a conduit à la découverte de la propagation des ondes. Équations généralisant les effets électromagnétiques ont constaté que la propagation à vitesse finie des champs E et B exigé certains comportements sur des particules chargées. L'étude générale des charges en mouvement constitue le potentiel Liénard-Wiechert, qui est une étape vers la relativité restreinte.
La transformation de Lorentz du champ électrique d'une charge en mouvement dans les résultats de cadre de référence d'un observateur non-déplacer dans l'apparition d'un terme mathématique communément appelé champ magn??tique. l'inverse, le magnétique champ généré par une charge en mouvement disparaît et devient purement électrostatique champ dans une comobile cadre de référence. Les équations de Maxwell sont donc tout simplement un ajustement empirique des effets relativistes spéciaux dans un modèle classique de l'Univers. Comme les champs électriques et magnétiques sont référentiel dépendante et donc entrelacés, on parle de électromagnétiques champs. La relativité spéciale fournit les règles de transformation pour la façon dont un champ électromagnétique dans un référentiel inertiel apparaît dans un autre référentiel inertiel.
Électromagnétisme dans 4D
Les équations de Maxwell dans la forme 3D sont déjà compatibles avec le contenu physique de la relativité restreinte. Mais nous devons les réécrire pour les rendre manifestement invariant.
Le densit?? de charge  et densité de courant
et densité de courant![[J_x,J_y,J_z] \!](../../images/531/53104.png) sont unifiés dans lecourant de charge 4-vecteur:
sont unifiés dans lecourant de charge 4-vecteur:
La loi de charger conservation, devient:
devient:
Lechamp électrique ![[E_x,E_y,E_z] \!](../../images/531/53108.png) et le induction magnétique
et le induction magnétique![[B_x,B_y,B_z] \!](../../images/531/53109.png) sont maintenant unifié dans le (rang 2 covariante antisymétrique)électromagnétique de tenseur de champ:
sont maintenant unifié dans le (rang 2 covariante antisymétrique)électromagnétique de tenseur de champ:
La densité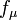 , de laforce de Lorentz,
, de laforce de Lorentz,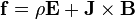 , exercée sur la matière par le champ électromagnétique devient:
, exercée sur la matière par le champ électromagnétique devient:
La loi de Faraday de l'induction, 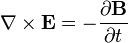 Et La loi de Gauss pour le magnétisme,
Et La loi de Gauss pour le magnétisme,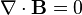 se combinent pour former:
se combinent pour former:
Bien qu'il semble y avoir 64 équations ici, mais réduit à seulement quatre équations indépendantes. Utilisation de l'antisymétrie du champ électromagnétique, on peut soit réduire à une identité (0 = 0) ou de rendre redondants toutes les équations, sauf pour ceux avec ??, ??, ?? = soit 1,2,3 ou 2,3,0 ou 3, 0,1 ou 0,1,2.
Le d??placement ??lectrique ![[D_x,D_y,D_z] \!](../../images/531/53117.png) et le champ magn??tique
et le champ magn??tique ![[H_x,H_y,H_z] \!](../../images/531/53118.png) sont maintenant unifiées dans le (rang 2 de contravariante antisymétrique) électromagnétique déplacement tenseur:
sont maintenant unifiées dans le (rang 2 de contravariante antisymétrique) électromagnétique déplacement tenseur:
La loi d'Ampère,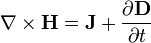 etla loi de Gauss,
etla loi de Gauss,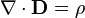 , se combinent pour former:
, se combinent pour former:
Dans le vide, leséquations constitutives sont:
Antisymétrie réduit ces 16 équations pour seulement six équations indépendantes.
Le densité d'énergie du champ électromagnétique se combine avec Poynting vecteur et le tenseur de Maxwell pour former le 4D électromagnétique tenseur-énergie. Il est le flux (densité) de l'élan 4-vecteur et un rang 2 tenseur mixte, il est:
o??  est le Kronecker.Lorsque indice supérieur est abaissé avec ??, il devient symétrique et fait partie de la source du champ gravitationnel.
est le Kronecker.Lorsque indice supérieur est abaissé avec ??, il devient symétrique et fait partie de la source du champ gravitationnel.
La conservation de quantité de mouvement et de l'énergie par le champ électromagnétique est exprimée par:
o?? 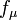 est de nouveau la densité du Force de Lorentz.Cette équation peut être déduite à partir des équations ci-dessus (avec un effort considérable).
est de nouveau la densité du Force de Lorentz.Cette équation peut être déduite à partir des équations ci-dessus (avec un effort considérable).
Statut
La relativité spéciale est exacte uniquement lorsque potentielle gravitationnelle est beaucoup moins que c 2 ; dans un fort champ gravitationnel il faut utiliser la relativité générale (qui devient la relativité restreinte à la limite du champ faible). À de très petites échelles, comme à la longueur de Planck et ci-dessous, les effets quantiques doivent être prises en considération pour résultat la gravit?? quantique. cependant, à des échelles macroscopiques et en l'absence de forts champs gravitationnels, la relativité restreinte est testé expérimentalement à très haut degré de précision (10 -20 ) et donc acceptée par la communauté de la physique. Les résultats expérimentaux qui semblent contredire ne sont pas reproductibles et sont donc largement soupçonnés d'être dus à des erreurs expérimentales.
En raison de la liberté on doit sélectionner la manière dont on définit les unités de longueur et de temps en physique, il est possible de faire l'une des deux postulats de la relativité d'uneconséquence tautologique des définitions, mais on ne peut le faire pour les deux postule simultanément, comme lorsque combinées, elles ont des conséquences qui sont indépendants de son choix de définition de la longueur et du temps.
La relativité spéciale est mathématiquement auto-cohérent, et il est une partie organique de toutes les théories physiques modernes, notammentla théorie quantique des champs,la théorie des cordes, et la relativité générale (dans le cas limite des champs gravitationnels négligeables).
Mécanique newtonienne suit mathématiquement à partir relativité restreinte à faibles vitesses (par rapport à la vitesse de la lumière) - ainsi la mécanique newtonienne peuvent être considérées comme une relativité spéciale des organes lents. Voir Statut de la relativité restreinte pour une discussion plus détaillée.
Quelques expériences clés peuvent être mentionnés qui a conduit à la relativité restreinte:
- Le Trouton expérience-Noble a montré que le couple exercé sur un condensateur est indépendante de la position et le cadre de référence inertiel - ces expériences ont conduit au premier postulat
- Le c??l??bre Expérience de Michelson-Morley a donné un appui supplémentaire au postulat que la détection d'une vitesse de référence absolue était pas réalisable. Il convient de préciser ici que, contrairement à de nombreux autres jeux de revendications, il dit peu de choses sur l'invariance de la vitesse de la lumière par rapport à la source et la vitesse de l'observateur, à la fois comme source et observateur voyageaient ensemble à la même vitesse en tout temps.
Un certain nombre d'expériences ont été menées pour tester la relativité spéciale contre les théories rivales. Ceux-ci comprennent:
- Expériences Kaufmann-Bucherer-Neumann - déviation électrons en accord approximatif avec la prédiction de Lorentz-Einstein.
- Expérience Fizeau - vitesse de la lumière dans le déplacement des médias en conformité avec plus de vitesse relativiste
- Expérience Kennedy-Thorndike - dilatation du temps en conformité avec les transformations de Lorentz
- Rossi-Hall expérience - effets relativistes sur la demi-vie d'une particule se déplaçant rapidement
- Des expériences pour testerla théorie d'émetteur ont démontré que la vitesse de la lumière est indépendante de la vitesse de l'émetteur.
- Hammar expérience - pas de "l'obstruction éther de flux"
En outre, les accélérateurs de particules accélèrent systématiquement et de mesurer les propriétés des particules se déplaçant à une vitesse proche de la lumière, où leur comportement est totalement compatible avec la théorie de la relativité et incompatible avec les précédentes mécanique newtonienne . Ces machines seraient tout simplement pas fonctionner si ils ne sont pas conçus selon les principes relativistes.
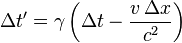
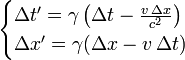






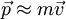
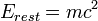




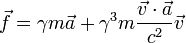
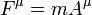
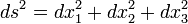





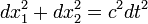
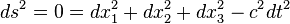

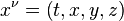
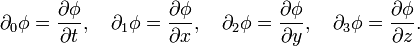
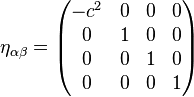
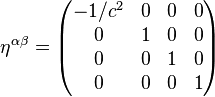


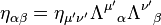
![T ^ {\ left [i_1 ', i_2', \ dots, i_p '\ right]} _ {\ left [j_1', j_2 ', \ dots, j_q' \ right]} = \ lambda ^ {i_1 '} { } _ {} i_1 \ Lambda ^ {i_2 '} {} {_ i_2} \ cdots \ Lambda ^ {i_p'} {} {_ i_p} \ {lambda_ j_1 '} {} ^ {j_1} \ {lambda_ j_2' } {} ^ {} j_2 \ cdots \ {lambda_ j_q '} {} ^ {} j_q T ^ {\ left [i_1, i_2, \ dots, i_p \ droite]} _ {\ left [j_1, j_2, \ dots , j_q \ right]}](../../images/530/53082.png)