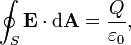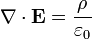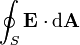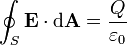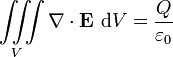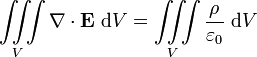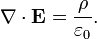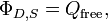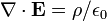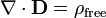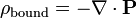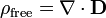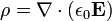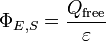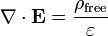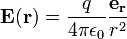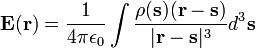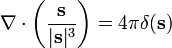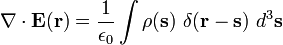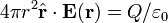La loi de Gauss

Sujets connexes: l'??lectricit?? et de l'??lectronique

Renseignements g??n??raux

Enfants SOS offrent un chargement complet de la s??lection pour les ??coles pour une utilisation sur les intranets des ??coles. Cliquez ici pour en savoir plus sur le parrainage d'enfants.

Electromagn??tisme

??lectricit?? Magn??tisme
??lectrostatique Charge ??lectrique ??lectricit?? statique Champ ??lectrique Conducteur Isolant Tribo??lectricit?? D??charge ??lectrostatique Induction La loi de Coulomb La loi de Gauss Flux ??lectrique / ??nergie potentielle Moment dipolaire ??lectrique Polarisation
Magn??tostatique La loi d'Amp??re Champ magn??tique Magn??tisation Flux magn??tique Loi de Biot-Savart Moment de dip??le magn??tique La loi de Gauss ?? magn??tisme
??lectrodynamique Droit de la force de Lorentz Induction ??lectromagn??tique La loi de Faraday La loi de Lenz D??placement actuel Les ??quations de Maxwell Champ ??lectromagn??tique Un rayonnement ??lectromagn??tique Tenseur de Maxwell Vecteur de Poynting Potentiel Li??nard-Wiechert Les ??quations de Jefimenko ?? courant de Foucault
R??seau ??lectrique Courant ??lectrique Potentiel ??lectrique Tension R??sistance La loi d'Ohm circuit de la s??rie Circuit parall??le Courant continu Courant alternatif Force ??lectromotrice Capacitance Inductance Imp??dance Cavit??s r??sonnantes Guides d'ondes
Formulation covariante Tenseur ??lectromagn??tique ( tenseur-??nergie) Four ?? courant continu Potentiel ??lectromagn??tique ?? quatre
Les scientifiques Amp??re Coulomb Faraday Gauss Heaviside Henri Hertz Lorentz Maxwell Tesla Volta Weber ??rsted

Dans la physique , de la loi, ??galement connu sous le th??or??me de Gauss Gauss flux, est une loi relative ?? la distribution des charges ??lectriques r??sultant au champ ??lectrique . La loi de Gauss stipule que:

Le flux ??lectrique ?? travers toute surface ferm??e est proportionnelle ?? la joint charge ??lectrique .

La loi a ??t?? formul??e par Carl Friedrich Gauss en 1835, mais n'a pas ??t?? publi?? jusqu'en 1867. Il est l'un des quatre ??quations de Maxwell qui forment la base de ??lectrodynamique classique, les trois autres ??tant La loi de Gauss pour le magn??tisme, La loi d'induction de Faraday, et La loi d'Amp??re avec correction de Maxwell. La loi de Gauss peut ??tre utilis??e pour d??river la loi de Coulomb , et vice versa.

La loi de Gauss peut ??tre exprim?? sous sa forme int??grale:

$\ Oint_S \ mathbf {E} \ cdot \ mathrm {d} \ mathbf {A} = \ frac {Q} {\ varepsilon_0},$

o?? le c??t?? gauche de l'??quation est une int??grale de surface d??signant le flux ??lectrique ?? travers une surface ferm??e S, et le c??t?? droit de l'??quation est la charge totale d??limit??e par S divis?? par le constante ??lectrique.

La loi de Gauss a aussi une forme diff??rentielle:

$\ Nabla \ cdot \ mathbf {E} = \ frac {\ rho} {\ varepsilon_0}$

?? ∇ o?? E est le divergence du champ ??lectrique , et ρ est la la densit?? de charge.

Les formes int??grales et diff??rentielles sont li??s par le th??or??me de la divergence, aussi appel?? le th??or??me de Gauss. Chacune de ces formes peut aussi ??tre exprim??e de deux fa??ons: en termes de relation entre le champ ??lectrique E et la charge ??lectrique totale, ou en termes de champ ??lectrique de d??placement D et le charge ??lectrique libre.

La loi de Gauss a une similitude math??matique ??troite avec un certain nombre de lois dans d'autres domaines de la physique, comme La loi de Gauss pour le magn??tisme et Th??or??me de Gauss. En fait, ne importe quel " loi de l'inverse carr?? "peut ??tre formul?? d'une mani??re similaire ?? la loi de Gauss: Par exemple, la loi de Gauss se est essentiellement ??quivalente ?? l'inverse du carr?? loi de Coulomb , et Th??or??me de Gauss est essentiellement ??quivalente ?? l'inverse du carr?? La loi de la gravitation de Newton.

La loi de Gauss peut ??tre utilis?? pour d??montrer que tous les champs ??lectriques ?? l'int??rieur d'un Cage de Faraday ont une charge ??lectrique. La loi de Gauss est quelque chose d'un analogue ??lectrique La loi d'Amp??re, qui traite avec le magn??tisme.

En termes de charge totale

Forme int??grale

Pour un volume V de surface S, la loi de Gauss indique que

$\ Phi_ {E, S} = \ frac {Q} {\ varepsilon_0}$

o?? Φ _{E, S} est le flux ??lectrique ?? travers S, Q est la charge totale ?? l'int??rieur V, et ε ₀ est la constante ??lectrique. Le flux ??lectrique est donn??e par un surface int??grale sur S:

$\ Oint_S \ mathbf {E} \ cdot \ mathrm {d} \ mathbf {A}$

o?? E est le champ ??lectrique, d A est un vecteur repr??sentant un ??l??ment infinit??simal de la zone , et repr??sente l'?? produit scalaire ..

Application de la forme int??grale

Si le champ ??lectrique est connu partout, la loi de Gauss, il est assez facile, en principe, de trouver la r??partition de la charge ??lectrique: La charge dans une r??gion donn??e peut ??tre d??duite en int??grant le champ ??lectrique pour trouver le flux.

Cependant, beaucoup plus souvent, ce est le probl??me inverse qui doit ??tre r??solu: la distribution de charge ??lectrique est connue, et le champ ??lectrique a besoin d'??tre calcul??e. Ce est beaucoup plus difficile, car si vous connaissez le flux total ?? travers une surface donn??e, qui donne presque aucune information sur le champ ??lectrique, qui (pour tout ce que vous savez) pourrait aller dans et hors de la surface dans les mod??les arbitrairement compliqu??es.

Une exception est se il ya une sym??trie dans la situation, qui exige que le champ ??lectrique traverse la surface de mani??re uniforme. Ensuite, si le flux total est connu, le champ lui-m??me peut en d??duire ?? chaque point. Des exemples courants de sym??tries qui se pr??tent ?? la loi de Gauss comprennent sym??trie cylindrique, la sym??trie plane, et la sym??trie sph??rique. Voir l'article Surface de Gauss pour des exemples o?? ces sym??tries sont exploit??es pour calculer les champs ??lectriques.

Forme diff??rentielle

En forme diff??rentielle , la loi de Gauss d??clare:

$\ Mathbf {\ nabla} \ cdot \ mathbf {E} = \ frac {\ rho} {\ varepsilon_0}$

o?? ∇ ?? d??signe divergence, E est le champ ??lectrique, et ρ est la totale ??lectrique la densit?? de charge (y compris les frais ?? la fois libre et li??), et ε ₀ est la constante ??lectrique. Ce est math??matiquement ??quivalente ?? la forme int??grale, en raison de la th??or??me de la divergence.

??quivalence des formes int??grales et diff??rentielles

Les formes int??grales et diff??rentielles sont math??matiquement ??quivalente, par le th??or??me de la divergence. Voici l'argument plus sp??cifiquement:

La forme int??grale de la loi de Gauss est:

$\ Oint_S \ mathbf {E} \ cdot \ mathrm {d} \ mathbf {A} = \ frac {Q} {\ varepsilon_0}$

pour toute surface ferm??e S contenant une charge Q. Par le th??or??me de la divergence, cette ??quation est ??quivalente ??:

$\ Iiint \ limits_V \ nabla \ cdot \ mathbf {E} \ \ mathrm {d} V = \ frac {Q} {\ varepsilon_0}$

pour tout volume V contenant une charge Q. Par la relation entre la charge et la densit?? de charge, cette ??quation est ??quivalente ??:

$\ Iiint \ limits_V \ nabla \ cdot \ mathbf {E} \ \ mathrm {d} V = \ iiint \ limits_V \ frac {\ rho} {\ varepsilon_0} \ \ mathrm {d} V$

pour chaque volume V. Pour cette ??quation pour ??tre simultan??ment vraies pour chaque volume V possible, il est n??cessaire (et suffisante) pour les int??grandes soient ??gaux partout. Par cons??quent, cette ??quation est ??quivalente ??:

$\ Nabla \ cdot \ mathbf {E} = \ frac {\ rho} {\ varepsilon_0}.$

Ainsi, les formes int??grales et diff??rentielles sont ??quivalentes.

En termes de charge libre

Gratuit fonction de la charge li??e

La charge ??lectrique qui se pose dans les situations de manuels simples serait class?? comme "charge libre" -par exemple, la charge qui est transf??r??e dans l'??lectricit?? statique ou la charge d'un plaque de condensateur. En revanche, "la charge li??e" ne se pose que dans le contexte de des mat??riaux di??lectriques (polarisables). (Tous les mat??riaux sont polarisable dans une certaine mesure). Lorsque ces mat??riaux sont plac??s dans un champ ??lectrique externe, les ??lectrons restent li??s ?? leurs atomes respectifs, mais se d??placent d'une distance microscopique en r??ponse au champ, de sorte qu'ils ne sont plus sur un c??t?? de l'atome que l'autre. Tous ces d??placements microscopiques se additionnent pour donner une distribution nette macroscopique de charge, ce qui constitue la ??charge limite".

Bien au microscope, tous les frais est fondamentalement la m??me, il ya souvent des raisons pratiques de vouloir traiter diff??remment des charges li??es charge libre. Le r??sultat est que la loi plus ??fondamentale?? de Gauss, en termes de E, est parfois mis dans la forme ??quivalente ci-dessous, qui est en fonction de D et la charge autoris??e.

Forme int??grale

Cette formulation de la loi de Gauss indique que, pour chaque volume V dans l'espace, avec la surface S, l'??quation suivante est v??rifi??e:

$\ Phi_ {D, S} = Q _ {\ mathrm {libre}}, \!$

o?? Φ _{D, S} est le flux de la d??placement de champ ??lectrique D ?? S, Q et _gratuit est la charge libre contenu dans V. Le flux Φ _{D, S} est d??finie de mani??re analogue au flux Φ _{E, S} du champ ??lectrique E ?? S. Plus pr??cis??ment, elle est donn??e par l'int??grale de surface

$\ Phi_ {D, S} = \ oint_S \ mathbf {D} \ cdot \ mathrm {d} \ mathbf {A}.$

Forme diff??rentielle

La forme diff??rentielle de la loi de Gauss, impliquant la charge autoris??e, d??clare:

$\ Mathbf {\ nabla} \ cdot \ mathbf {D} = \ rho _ {\ mathrm {libre}}$

?? ∇ o?? D est le divergence du champ de d??placement ??lectrique, et ρ est la densit?? _libre sans charge ??lectrique.

Le formulaire de diff??rentiel et forme int??grale sont math??matiquement ??quivalent. La preuve consiste principalement ?? th??or??me de la divergence.

Equivalence des totaux et libres ??tats de charge

Preuve que les formulations de la loi de Gauss en termes de charge libre sont ??quivalentes aux formulations impliquant charge totale.

Dans cette preuve, nous allons montrer que l'??quation

$\ Nabla \ cdot \ mathbf {E} = \ rho / \ epsilon_0$

est ??quivalente ?? l'??quation

$\ Nabla \ cdot \ mathbf {D} = \ rho _ {\ mathrm {libre}}$

Notez que nous ne traitant qu'avec les formes diff??rentielles, pas les formes int??grales, mais ce est suffisant, car le diff??rentiel et formes int??grales sont ??quivalents dans chaque cas, par le th??or??me de la divergence.

Nous introduisons la densit?? polarisation P, qui a la relation suivante pour E et D:

$\ Mathbf {D} = \ epsilon_0 \ mathbf {E} + \ mathbf {P}$

et la relation suivante ?? la charge li??e:

$\ Rho _ {\ mathrm {}} li?? = - \ nabla \ cdot \ mathbf {P}$

Maintenant, consid??rons les trois ??quations:

$\ Rho _ {\ mathrm {}} li?? = \ nabla \ cdot (- \ mathbf {P})$

$\ Rho _ {\ mathrm {libre}} = \ nabla \ cdot \ mathbf {D}$

$\ Rho = \ nabla \ cdot (\ epsilon_0 \ mathbf {} E)$

L'id??e essentielle est que la somme des deux premi??res ??quations est la troisi??me ??quation. Ceci compl??te la preuve: La premi??re ??quation est vrai, par d??finition, et donc la seconde ??quation est vrai si et seulement si la troisi??me ??quation est vrai. Ainsi, les deuxi??me et troisi??me ??quations sont ??quivalentes, ce qui est ce que nous voulions prouver.

Dans les mat??riaux lin??aires

Dans homog??ne, isotrope, non dispersif, mat??riaux lin??aires, il ya une belle, simple relation entre E et D:

$\ Varepsilon \ mathbf {E} = \ mathbf {D}$

o?? ε est la permittivit?? du mat??riau. Dans ces conditions, il est encore une autre paire de formulations ??quivalentes de la loi de Gauss:

$\ Phi_ {E, S} = \ frac {Q _ {\ mathrm {libre}}} {\ varepsilon}$

$\ Mathbf {\ nabla} \ cdot \ mathbf {E} = \ frac {\ rho _ {\ mathrm {libre}}} {\ varepsilon}$

Rapport ?? la loi de Coulomb

Issu de la loi de Gauss de la loi de Coulomb

La loi de Gauss peut ??tre d??duite de la loi de Coulomb , qui stipule que le champ ??lectrique d?? ?? un arr??t charge ponctuelle est:

$\ Mathbf {E} (\ mathbf {r}) = \ frac {q} {4 \ pi \ epsilon_0} \ frac {\ mathbf {e_r}} {r ^ 2}$

o??

e _r est le radiale vecteur unit??,

r est le rayon, | r |,

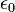$\ Epsilon_0$ est le constante ??lectrique,

q est la charge de la particule, qui est suppos?? ??tre situ?? ?? la origine.

En utilisant l'expression de la loi de Coulomb, nous obtenons le champ total au r en utilisant une partie int??grante de la somme du champ au r due ?? la charge infinit??simale ?? chaque autre point s dans l'espace, pour donner

$\ Mathbf {E} (\ mathbf {r}) = \ frac {1} {4 \ pi \ epsilon_0} \ int \ frac {\ rho (\ mathbf {s}) (\ mathbf {r} - \ mathbf {s })} {| \ mathbf {r} - \ mathbf {s} | ^ 3 ^ 3} d \ mathbf {s}$

o?? $\ Rho$ est la densit?? de charge. Si nous prenons la divergence des deux c??t??s de cette ??quation par rapport ?? r, et utilisons le th??or??me connu

$\ Nabla \ cdot \ left (\ frac {\ mathbf {s}} {| \ mathbf {s} | ^ 3} \ right) = 4 \ pi \ delta (\ mathbf {s})$

o?? δ (s) est la Fonction delta de Dirac, le r??sultat est

$\ Nabla \ cdot \ mathbf {E} (\ mathbf {r}) = \ frac {1} {\ epsilon_0} \ int \ rho (\ mathbf {s}) \ \ delta (\ mathbf {r} - \ mathbf { s}) \ d ^ 3 \ mathbf {s}$

En utilisant le " tamisage propri??t?? "de la fonction de Dirac, nous arrivons ??

$\ Nabla \ cdot \ mathbf {E} (\ mathbf {r}) = \ rho (\ mathbf {r}) / \ epsilon_0$

qui est la forme diff??rentielle de la loi de Gauss, comme on le souhaite.

Notez que, depuis la loi de Coulomb se applique uniquement aux charges fixes, il ne ya aucune raison de se attendre ?? la loi de Gauss de tenir des frais fond?? sur cette seule d??rivation d??placer. En fait, la loi de Gauss ne d??tient des charges en mouvement, et ?? cet ??gard la loi de Gauss est plus g??n??rale que la loi de Coulomb.

Issu de la loi de Coulomb de la loi de Gauss

Strictement parlant, la loi de Coulomb ne peut ??tre d??riv?? de la loi de Gauss seul, depuis la loi de Gauss ne donne aucune information concernant la boucle de E (voir D??composition de Helmholtz et La loi de Faraday). Cependant, la loi de Coulomb peut ??tre d??montr?? ?? partir de la loi de Gauss si l'on suppose, en outre, que le champ ??lectrique ?? partir d'un charge ponctuelle est sph??rique sym??trique (cette hypoth??se, comme la loi de Coulomb lui-m??me, est tout ?? fait vrai si la charge est fixe, et approximativement vrai si la charge est en mouvement).

Prenant S dans la forme int??grale de la loi de Gauss pour ??tre une surface sph??rique de rayon r, centr??e au point charge Q, nous avons

$\ Oint_ {S} \ mathbf {E} \ cdot d \ mathbf {A} = Q / \ varepsilon_0$

Par l'hypoth??se de sym??trie sph??rique, l'int??grale est une constante qui peut ??tre retir?? de l'int??grale. Le r??sultat est

$4 \ pi r ^ 2 \ hat {\ mathbf {r}} \ cdot \ mathbf {E} (\ mathbf {r}) = Q / \ varepsilon_0$

o?? $\ Hat {\ mathbf {r}}$ est un vecteur unitaire pointant radialement ?? l'??cart de la charge. Encore une fois par sym??trie sph??rique, points de E dans la direction radiale, et ainsi nous sommes

$\ Mathbf {E} (\ mathbf {r}) = \ frac {Q} {4 \ pi \ varepsilon_0} \ frac {\ hat {\ mathbf {r}}} {r ^ 2}$

qui est essentiellement ??quivalente ?? la loi de Coulomb. Ainsi, la l'inverse du carr?? de d??pendance de la loi du champ ??lectrique dans la loi de Coulomb d??coule de la loi de Gauss.

R??cup??r?? ?? partir de " http://en.wikipedia.org/w/index.php?title=Gauss%27s_law&oldid=409897377 "