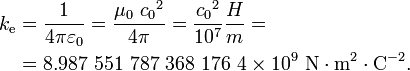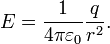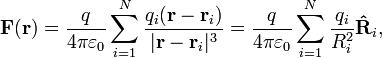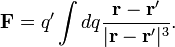La loi de Coulomb
Contexte des ??coles Wikip??dia
SOS croit que l'??ducation donne une meilleure chance dans la vie des enfants dans le monde en d??veloppement aussi. Pour comparer les organismes de bienfaisance de parrainage ce est le meilleur lien de parrainage .
| Electromagn??tisme |
|---|
 |
??lectrostatique
|
|
Magn??tostatique
|
??lectrodynamique
|
R??seau ??lectrique
|
Formulation covariante Tenseur ??lectromagn??tique ( tenseur-??nergie)
|
La loi de Coulomb, parfois appel?? la loi de Coulomb, est une ??quation d??crivant la force ??lectrostatique entre les charges ??lectriques . Il a ??t?? d??velopp?? dans les ann??es 1780 par le physicien fran??ais Charles Augustin de Coulomb et a ??t?? essentielle au d??veloppement de la th??orie de l'??lectromagn??tisme. La loi de Coulomb peut ??tre indiqu?? dans forme scalaire comme suit:
- La grandeur de la force ??lectrostatique entre deux signaler charges ??lectriques est directement proportionnelle au produit des amplitudes de chacune des charges et inversement proportionnelle au carr?? de la distance totale entre les deux charges.
Forme Scalar


Le forme scalaire de la loi de Coulomb ne d??crire l'ampleur de la force ??lectrostatique entre deux charges ??lectriques. Si la direction est n??cessaire, alors la forme de vecteur est n??cessaire ainsi. La grandeur de la force ??lectrostatique (F) sur une charge (Q 1) due ?? la pr??sence d'une seconde charge (Q 2), est donn??e par
o?? r est la distance entre les deux charges et e k une constante de proportionnalit??. Une force positive implique une interaction r??pulsive, tandis qu'une force n??gative implique une interaction attractive.
La constante de proportionnalit?? k e, appel??e la constante de Coulomb est li??e ?? la propri??t??s de l'espace et peuvent ??tre calcul??s exactement:
En Unit??s SI la vitesse de la lumi??re dans le vide , not??e c 0 est d??fini comme 299792458 m ?? s -1, et la constante magn??tique (μ 0) est d??finie comme 4π x 10 -7 H ?? m -1, conduisant ?? la d??finition de la constante ??lectrique (ε 0) et ε 0 = 1 / (μ 0 c 2
0) ≈ 8,854 1 87 17 8 x 10 -12 F ?? m -1. En unit??s CGS, l'unit?? de taxe, frais ou esu Statcoulomb, est d??fini de telle sorte que cette constante de force de Coulomb est 1.
Cette formule indique que l'amplitude de la force est directement proportionnelle ?? l'amplitude des charges de chaque objet et inversement proportionnelle au carr?? de la distance entre eux. L'exposant dans la loi de Coulomb a ??t?? trouv?? pour diff??rer de -2 de moins de un sur un milliard.
Lorsque mesur?? en unit??s que les gens utilisent souvent (comme SI-voir Syst??me international d'unit??s), la constante de force ??lectrostatique (k e) est num??riquement beaucoup, beaucoup plus grand que le constante de gravitation universelle (G). Cela signifie que pour des objets de charge qui est de l'ordre d'une unit?? de charge (C) et la masse de l'ordre d'une unit?? de masse (en kg), les forces ??lectrostatiques sera d'autant plus grande que les forces gravitationnelles que cette derni??re force peut ??tre ignor??es. Ce ne est pas le cas lorsque Unit??s de Planck sont utilis??s et les deux charge et la masse sont de l'ordre de la charge de l'unit?? et de la masse de l'appareil. Cependant, charg?? particules ??l??mentaires ont une masse qui est beaucoup moins que la masse de Planck alors que leur charge est d'environ la charge Planck de sorte que, ?? nouveau, les forces gravitationnelles peuvent ??tre ignor??s. Par exemple, la force ??lectrostatique entre un ??lectron et un proton , ce qui constitue un hydrog??ne atome est presque 40 ordres de grandeur sup??rieure ?? la force gravitationnelle entre eux.
La loi de Coulomb peut ??galement ??tre interpr??t?? en termes de unit??s atomiques avec la force exprim??s en Hartrees par Rayon de Bohr, la charge en termes de charge ??l??mentaire, et les distances en termes de rayon de Bohr.
Champ ??lectrique
Il r??sulte de ce Droit force de Lorentz que l'ampleur de la champ ??lectrique (E) cr????e par une charge ponctuelle unique (q) ?? une certaine distance (r) est donn?? par:
Pour une charge positive, la direction des points de champ ??lectrique le long des lignes dirig?? radialement loin de l'emplacement de la charge ponctuelle, tandis que la direction est l'inverse pour une charge n??gative. Le Unit??s SI de champ ??lectrique sont volts par m??tre ou newtons par coulomb.
formulaire de Vector
Afin d'obtenir ?? la fois l'ampleur et la direction de la force sur une charge,  ?? la position
?? la position 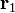 , Conna??t un champ en raison de la pr??sence d'une autre charge, q 2 ?? la position
, Conna??t un champ en raison de la pr??sence d'une autre charge, q 2 ?? la position  , La pleine vecteur forme de la loi de Coulomb est n??cessaire.
, La pleine vecteur forme de la loi de Coulomb est n??cessaire.
o??  est la s??paration des deux charges. Notez que ce est tout simplement la d??finition de scalaire de la loi de Coulomb avec la direction donn??e par le vecteur unit??,
est la s??paration des deux charges. Notez que ce est tout simplement la d??finition de scalaire de la loi de Coulomb avec la direction donn??e par le vecteur unit??,  , Parall??le ?? la ligne de la charge
, Parall??le ?? la ligne de la charge 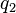 charger
charger  .
.
Si les deux charges ont la m??me signer (comme les frais), alors la produit  est positive et la direction de la force sur
est positive et la direction de la force sur  est donn??e par
est donn??e par  ; les charges identiques se repoussent les uns les autres. Si les charges sont de signes oppos??s puis l'produits
; les charges identiques se repoussent les uns les autres. Si les charges sont de signes oppos??s puis l'produits  est n??gative et la direction de la force sur
est n??gative et la direction de la force sur  est donn??e par
est donn??e par 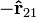 ; les charges se attirent.
; les charges se attirent.
Syst??me de charges discr??tes
Le principe de superposition lin??aire peut ??tre utilis??e pour calculer la force sur une petite charge d'essai, 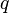 , Gr??ce ?? un syst??me de
, Gr??ce ?? un syst??me de  charges discr??tes:
charges discr??tes:
o??  et
et  sont l'amplitude et la position respectivement de la
sont l'amplitude et la position respectivement de la 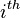 frais,
frais,  est un vecteur unitaire dans la direction de
est un vecteur unitaire dans la direction de  (Un vecteur pointant de frais
(Un vecteur pointant de frais  charger
charger 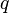 ), Et
), Et  est l'amplitude de
est l'amplitude de 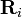 (La s??paration entre les charges
(La s??paration entre les charges  et
et 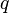 ).
).
Distribution de charge continu
Pour une distribution de charge une partie int??grante sur la r??gion contenant la charge est ??quivalente ?? une somme infinie, traitant chaque ??l??ment infinit??simal de l'espace comme une charge ponctuelle  .
.
Pour une distribution de charge lin??aire (une bonne approximation pour la charge dans un fil) o??  donne la charge par unit?? de longueur ?? la position
donne la charge par unit?? de longueur ?? la position 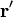 Et
Et  est un ??l??ment infinit??simal de longueur,
est un ??l??ment infinit??simal de longueur,
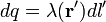 .
.
Pour une distribution de charge de surface (une bonne approximation pour la charge sur une plaque dans une plaque parall??le condensateur) o?? 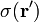 donne la charge par unit?? de surface ?? la position
donne la charge par unit?? de surface ?? la position 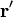 Et
Et 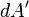 est un ??l??ment infime de la zone,
est un ??l??ment infime de la zone,
Pour une distribution de charge de volume (comme la charge dans un m??tal en vrac) o?? 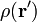 donne la charge par unit?? de volume ?? la position
donne la charge par unit?? de volume ?? la position 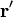 Et
Et 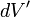 est un ??l??ment infime du volume,
est un ??l??ment infime du volume,
La force exerc??e sur une petite charge d'essai  ?? la position
?? la position  est donn??e par
est donn??e par
Repr??sentation graphique
Ci-dessous est une repr??sentation graphique de la loi de Coulomb, lorsque 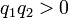 . Le vecteur
. Le vecteur  est la force v??cue par
est la force v??cue par  . Le vecteur
. Le vecteur  est la force v??cue par
est la force v??cue par  . Leur magnitude seront toujours ??gale. Le vecteur
. Leur magnitude seront toujours ??gale. Le vecteur  est le vecteur de d??placement entre deux charges (
est le vecteur de d??placement entre deux charges (  et
et 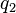 ).
).

Rapprochement ??lectrostatique
Dans les deux formulation, la loi de Coulomb est tout ?? fait exact que lorsque les objets sont ?? l'arr??t, et reste ?? peu pr??s correcte seulement pour mouvement lent. Ces conditions sont collectivement connus sous le nom approximation ??lectrostatique. Lorsque le mouvement a lieu, les champs magn??tiques sont produits qui modifient la force sur les deux objets. L'interaction magn??tique entre les charges en mouvement peut ??tre consid??r?? comme une manifestation de la force du champ ??lectrostatique mais avec Einstein de l ' th??orie de la relativit?? pris en consid??ration.
Table des grandeurs d??riv??es
| propri??t?? d'une particule | Relations | La propri??t?? field | |||||
| quantit?? de Vector |
|  |
| ||||
| Relations |  |  | |||||
| Quantit?? scalaire |
|  |
|