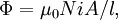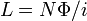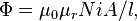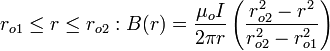Inductance
?? propos de ce ??coles s??lection Wikipedia
Les articles de cette s??lection ??coles ont ??t?? organis??s par sujet du programme d'??tudes gr??ce aux b??n??voles d'enfants SOS. Cliquez ici pour en savoir plus sur le parrainage d'enfants.
| Electromagn??tisme |
|---|
 |
??lectrostatique
|
Magn??tostatique
|
??lectrodynamique
|
R??seau ??lectrique
|
Formulation covariante Tenseur ??lectromagn??tique ( tenseur-??nergie)
|
Dans l'??lectromagn??tisme et de l'??lectronique , l'inductance est la propri??t?? d'un conducteur par lequel un changement de courant dans le conducteur "induit" (cr??e) un tension ( force ??lectromotrice) ?? la fois le conducteur lui-m??me (self) et dans tous les conducteurs ?? proximit?? (inductance mutuelle). Cet effet provient de deux observations fondamentales de la physique: premi??rement, un courant stable cr??e un champ magn??tique constant ( De Oersted law) et, deuxi??mement, un champ magn??tique variable dans le temps induit une tension dans un conducteur ?? proximit?? ( La loi de Faraday de l'induction). ?? partir de La loi de Lenz, dans un circuit ??lectrique, un courant ??lectrique ?? travers un changement de circuit qui a une inductance induit une tension proportionnelle qui se oppose au changement de courant (self). Le champ variable dans ce circuit peut ??galement induire une fem dans un circuit (inductance mutuelle) voisin.
Le terme ??inductance?? a ??t?? invent?? par Oliver Heaviside en F??vrier 1886. Il est de coutume d'utiliser le symbole L pour l'inductance, en l'honneur du physicien Heinrich Lenz. Dans le SI syst??me de l'unit?? est l'inductance henry, nomm?? en l'honneur du scientifique qui a d??couvert l'inductance, Joseph Henry.
Pour ajouter un circuit ?? inductance, ou ??lectrique des composants ??lectroniques appel??s inductances sont utilis??s, typiquement constitu?? de bobines de fil pour concentrer le champ magn??tique et de sorte que le champ magn??tique est reli?? dans le circuit plus d'une fois.
La relation entre la self L d'un circuit ??lectrique henrys, la tension et le courant est
o?? v d??signe la tension en volts et je le courant en amp??res. La tension aux bornes d'une inductance est ??gal au produit de son inductance et le taux de temps de changement du courant ?? travers elle.
Tous les circuits pratiques ont une inductance, qui peuvent fournir des effets b??n??fiques ou n??fastes. Dans un circuit accord?? inductance est utilis?? pour fournir un circuit s??lectif en fr??quence. Inducteurs auxiliaires peuvent ??tre utilis??s pour fournir la filtration ou le stockage d'??nergie dans un syst??me. L'inductance d'un ligne de transmission est une des propri??t??s qui d??termine son imp??dance caract??ristique; ??quilibrer l'inductance et capacit?? des c??bles est important pour sans distorsion la t??l??graphie et t??l??phonie. L'inductance de lignes de transmission d'??lectricit?? ?? long limite la puissance AC qui peut ??tre envoy?? sur eux. Circuits sensibles tels que microphone et c??bles de r??seaux informatiques peuvent utiliser des constructions de c??bles sp??ciaux pour limiter l'inductance mutuelle entre les circuits de signaux.
Dans l'analyse de circuit
La g??n??ralisation au cas de K circuits ??lectriques avec des courants i m et tensions V m lit
Inductance ici est une matrice sym??trique. La diagonale coefficients L m, m sont appel??s coefficients de self, les ??l??ments hors diagonale sont appel??s coefficients de mutuelle inductance. Les coefficients d'inductance sont constants tant qu'aucun mat??riau magn??tisable ayant des caract??ristiques non lin??aires est impliqu??. Ceci est une cons??quence directe de la lin??arit?? des ??quations de Maxwell dans les champs et la densit?? de courant. Les coefficients des fonctions inductance deviennent des courants dans le cas non-lin??aire, voir inductance non lin??aire .
D??rivation ?? partir de la loi de Faraday de l'inductance
Les ??quations d'inductance ci-dessus sont une cons??quence de les ??quations de Maxwell . Il est une d??rivation simple dans le cas important des circuits ??lectriques constitu??s de fils minces.
Consid??rons un syst??me de K boucles de fil, chacun avec un ou plusieurs spires de fil. Le liaison de flux de la boucle m est donn??e par
Voici N m d??signe le nombre de tours dans la boucle m, Φ m le flux magn??tique ?? travers cette boucle, et L m, n sont des constantes. Cela r??sulte de l'??quation La loi d'Amp??re - champs magn??tiques et les flux sont des fonctions lin??aires des courants. Par La loi de Faraday de l'induction nous avons
o?? v m est la tension induite dans le circuit m. Ceci est en accord avec la d??finition ci-dessus de l'inductance L si les coefficients m, n sont identifi??s par les coefficients de l'inductance. Etant donn?? que les courants totaux N n i n contribuent ?? Φ m il se ensuit ??galement que L m, n est proportionnelle au produit de spires N m N n.
Inductance et l'??nergie de champ magn??tique
En multipliant l'??quation ci-dessus pour v m avec i m dt et en sommant sur m donne l'??nergie transf??r??e au syst??me dans l'intervalle de temps dt,
Ce doit ??tre d'accord avec le changement de la W d'??nergie de champ magn??tique provoqu?? par les courants. La condition d'int??grabilit??
exige L m, n = L n, m. La matrice de l'inductance L m, n ainsi est sym??trique. L'int??grale du transfert d'??nergie est l'??nergie du champ magn??tique en fonction des courants,
Cette ??quation est aussi une cons??quence directe de la lin??arit?? des ??quations de Maxwell. Il est utile d'associer la modification des courants ??lectriques avec une accumulation ou une diminution de l'??nergie de champ de l'aimant. Le transfert d'??nergie correspondant exige ou g??n??re une tension. Une analogie m??canique dans le cas K = 1 avec de l'??nergie de champ magn??tique (2.1) Li 2 est un corps de masse M, u la vitesse et l'??nergie cin??tique (1/2) 2 Mu. Le taux de variation de vitesse (actuelle) multipli?? par la masse (inductance) exige ou g??n??re une force (une tension ??lectrique).
Inducteurs coupl??s

Inductance mutuelle se produit lorsque la variation de courant dans une bobine d'induction induit une tension dans un autre inducteur ?? proximit??. Il est important que le m??canisme par lequel transformateurs travaillent, mais il peut aussi provoquer un couplage ind??sirable entre conducteurs dans un circuit.
L'inductance mutuelle M, est ??galement une mesure du couplage entre deux inducteurs. L'inductance mutuelle par le circuit sur le circuit i j est donn??e par l'int??grale double Formule Neumann, voir techniques de calcul
L'inductance mutuelle a ??galement la relation:
o??
 est l'inductance mutuelle, et l'indice indique le rapport de la tension induite dans la bobine 2 en raison du courant dans la bobine 1.
est l'inductance mutuelle, et l'indice indique le rapport de la tension induite dans la bobine 2 en raison du courant dans la bobine 1. - N 1 est le nombre de spires dans la bobine 1,
- N 2 est le nombre de spires dans la bobine 2,
- P 21 est la perm??ance de l'espace occup?? par le flux.
L'inductance mutuelle a ??galement une relation avec le coefficient de couplage. Le coefficient de couplage est toujours comprise entre 0 et 1, et est un moyen pratique pour sp??cifier la relation entre une certaine orientation des inductances avec des inductances arbitraire:
o??
- k est le coefficient de couplage et 0 ≤ k ≤ 1,
- L 1 est l'inductance de la premi??re bobine, et
- L 2 est l'inductance de la deuxi??me bobine.
Une fois que la mutuelle inductance, M, est d??termin??e ?? partir de ce facteur, il peut ??tre utilis?? pour pr??dire le comportement d'un circuit:
o??
- V 1 est la tension aux bornes de l'inducteur d'int??r??t,
- L 1 est l'inductance de l'inducteur d'int??r??t,
- I d 1 / d t est la d??riv??e par rapport au temps, du courant dans l'inductance d'int??r??t,
- d 2 I / dt est la d??riv??e par rapport au temps, du courant dans l'inductance qui est coupl??e ?? la premi??re inductance, et
- M est l'inductance mutuelle.
Le signe moins se pose parce que le sens du courant I 2 a ??t?? d??fini dans le sch??ma. Avec les deux courants d??fini entrer dans les points le signe de M sera positif.
Quand une bobine d'inductance est ??troitement coupl?? ?? un autre inducteur par inductance mutuelle, tel que dans une transformateur, les tensions, les courants, et le nombre de tours peuvent ??tre li??s de la mani??re suivante:
o??
- V s est la tension aux bornes de l'inductance secondaire,
- V p est la tension aux bornes de l'inducteur primaire (l'une reli??e ?? une source de courant),
- N s est le nombre de spires de l'inducteur secondaire, et
- N p est le nombre de spires de l'inducteur primaire.
A l'inverse le courant:
o??
- I s est le courant dans l'inductance secondaire,
- Ip est le courant ?? travers l'inductance primaire (celle qui est connect??e ?? une source de courant),
- N s est le nombre de spires de l'inducteur secondaire, et
- N p est le nombre de spires de l'inducteur primaire.
Notez que la puissance ?? travers une bobine d'induction est la m??me que la puissance ?? travers l'autre. Notez ??galement que ces ??quations ne fonctionnent pas si les deux transformateurs sont oblig??s (des sources d'??nergie).
Lorsque part et d'autre du transformateur est un circuit accord??, le montant de la mutuelle inductance entre les deux enroulements d??termine la forme de la courbe de r??ponse en fr??quence. Bien que pas de fronti??res sont d??finies, ce qui est souvent d??sign?? sous loose-, criticit??, et plus de couplage. Lorsque deux circuits accord??s sont coupl??s de mani??re l??che dans l'inductance mutuelle, la bande passante sera ??troite. Comme le montant des augmentations inductance communs de placement, la bande passante ne cesse de cro??tre. Lorsque la mutuelle inductance est augment??e au-del?? d'un point critique, le pic de la courbe de r??ponse commence ?? baisser, et la fr??quence centrale sera att??nu?? plus fortement que ses bandes lat??rales directs. Ceci est connu comme surcouplage.
techniques de calcul
Dans le cas le plus g??n??ral, l'inductance peut ??tre calcul??e ?? partir des ??quations de Maxwell. De nombreux cas importants peuvent ??tre r??solus en utilisant des simplifications. O?? les courants haute fr??quence sont consid??r??es, avec effet de peau, les densit??s de courant de surface et le champ magn??tique peut ??tre obtenu par r??solution de l'??quation de Laplace. Lorsque les conducteurs sont des fils minces, self inductance d??pend encore sur le rayon de fil et la distribution du courant dans le fil. Cette r??partition du courant est sensiblement constante (en surface ou dans le volume du fil) pour un rayon beaucoup plus petit que les autres ??chelles de longueur de fil.
Inductance mutuelle de deux boucles de fil
L'inductance mutuelle par un circuit filamentaire i sur un circuit filamentaire j est donn??e par l'int??grale double Formule Neumann
Le symbole μ 0 d??signe la constante magn??tique (4π x 10 -7 H / m), C i et C j sont les courbes engendr?? par les fils, R ij est la distance entre deux points. Voir un d??rivation de cette ??quation.
Auto-inductance d'une boucle de fil
Formellement, la self-inductance d'une boucle de fil serait donn??e par l'??quation ci-dessus avec i = j. Le probl??me, cependant, est que 1 / R devient infini, ce qui rend n??cessaire de prendre le rayon fini et un fil de la distribution du courant dans le fil en compte. Il reste la contribution de l'int??grale sur tous les points avec | R |> un terme / 2 et une correction,
Ici, un rayon et l d??signent et de longueur du fil, et Y est une constante qui d??pend de la distribution du courant dans le fil: Y = 0 lorsque le courant circule dans la surface du fil ( effet de peau), Y = 1/4 lorsque le courant est homog??ne ?? travers le fil. Cette approximation est exacte lorsque les fils sont longues par rapport ?? leurs dimensions transversales.
Proc??d?? d'images
Dans certains cas, les diff??rentes distributions actuelles g??n??rent le m??me champ magn??tique dans une certaine partie de l'espace. Ce fait peut ??tre utilis?? pour relier selfs ( Proc??d?? d'images). A titre d'exemple examiner les deux syst??mes:
- Un fil ?? une distance d / 2 en face d'un mur parfaitement conducteur (qui est le retour)
- Deux fils parall??les ?? distance d, avec un courant oppos??
Le champ magn??tique des deux syst??mes co??ncide (en une demi-espace). L'??nergie du champ magn??tique et l'inductance du second syst??me sont donc deux fois plus grande que celle du premier syst??me.
Relation entre inductance et capacit??
Inductance par longueur L 'et capacit?? par longueur C 'sont li??s les uns aux autres dans le cas particulier de lignes de transmission compos?? de deux conducteurs parfaits parall??les de section transversale arbitraire, mais constante,
Voici ε et μ d??signe la constante di??lectrique et la perm??abilit?? magn??tique du support les conducteurs sont noy??s dans. Il ne est pas ??lectrique et l'absence de champ magn??tique ?? l'int??rieur des conducteurs (complet effet de peau, haute fr??quence). Le courant circule vers le bas sur une ligne et retourne sur l'autre. Les signaux se propagent le long de la ligne de transmission ?? la vitesse d'un rayonnement ??lectromagn??tique dans le milieu non conducteur enveloppant les conducteurs.
Auto-inductance de circuits ??lectriques simples dans l'air
L'auto-inductance de nombreux types de circuits ??lectriques peut ??tre donn??e sous forme ferm??e. Des exemples sont donn??s dans le tableau.
| Type | Inductance | Commentaire |
|---|---|---|
| Simple couche sol??no??de | 
|  : Nombre de tours : Nombre de tours r: rayon L: longueur w = r / l 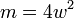  : Int??grales elliptiques : Int??grales elliptiques |
| C??ble coaxial, haute fr??quence |  | 1: Rayon ext??rieur a: Rayon interne L: longueur |
| Boucle circulaire |  | r: boucle rayon a: rayon de fil |
| Rectangle |  | b, d: longueur des fronti??res d >> a, b >> un a: rayon de fil |
| Paire de parall??le fils |  | a: rayon de fil d: Distance, d ≥ 2a L: longueur de la paire |
| Paire de parall??le fils, haute fr??quence |  | a: rayon de fil d: Distance, d ≥ 2a L: longueur de la paire |
| Fil parall??le ?? parfaitement paroi conductrice |  | a: rayon de fil d: Distance, d ≥ a L: longueur |
| Fil parall??le ?? paroi conductrice, haute fr??quence | 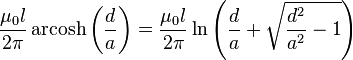 | a: rayon de fil d: Distance, d ≥ a L: longueur |
Le symbole μ 0 d??signe la magn??tique constant (4π ?? 10 -7 H / m). Pour les hautes fr??quences, le courant ??lectrique circule dans la surface du conducteur ( ??corcher effet), et en fonction de la g??om??trie, il est parfois n??cessaire de distinguer inductances basses et hautes fr??quences. Ce est l'objet de la constante Y: Y = 0 lorsque le courant est r??parti uniform??ment sur la surface du fil (effet de peau), Y = 1/4 lorsque le courant est r??parti uniform??ment sur la section transversale du fil. Dans le cas de haute fr??quence, si les conducteurs se rapprochent, un courant de d??pistage des flux suppl??mentaires dans leur surface, et des expressions contenant Y devenir invalide.
Inductance avec sym??trie physique
Inductance d'un sol??no??de
Un sol??no??de est long, mince bobine, ?? savoir une bobine dont la longueur est beaucoup plus grande que le diam??tre. Dans ces conditions, et sans aucun mat??riau magn??tique utilis??, le densit?? de flux magn??tique 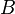 dans la bobine est pratiquement constante et est donn??e par
dans la bobine est pratiquement constante et est donn??e par
o??  est le magn??tique constant,
est le magn??tique constant,  le nombre de spires,
le nombre de spires,  le courant et
le courant et  la longueur de la bobine. En ignorant les effets d'extr??mit?? du flux magn??tique ?? travers la bobine totale est obtenue en multipliant la densit?? de flux
la longueur de la bobine. En ignorant les effets d'extr??mit?? du flux magn??tique ?? travers la bobine totale est obtenue en multipliant la densit?? de flux 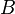 par l'aire de section transversale
par l'aire de section transversale  et le nombre de spires
et le nombre de spires  :
:
Lorsque cela est combin?? avec la d??finition de l'inductance,
il se ensuit que l'inductance d'une bobine est donn??e par:
Une table d'inductance pour sol??no??des courts de diff??rents diam??tres des ratios de longueur a ??t?? calcul??e par Dellinger, Whittmore et Ould
Ceci, et l'inductance de formes plus compliqu??es, peut ??tre d??riv?? d' ??quations de Maxwell . Pour rigides bobines ?? noyau d'air, l'inductance est une fonction de la g??om??trie de bobine et le nombre de spires, et est ind??pendante du courant.
Une analyse similaire se applique ?? un ??lectro-aimant avec un noyau magn??tique, mais seulement si la longueur de la bobine est tr??s sup??rieur au produit de la perm??abilit?? relative du noyau magn??tique et le diam??tre. Cela limite l'analyse simple ?? noyaux ?? faible perm??abilit??, ou extr??mement longues sol??no??des minces. Bien que rarement utile, les ??quations sont,
o??  la perm??abilit?? relative du mat??riau ?? l'int??rieur du sol??no??de,
la perm??abilit?? relative du mat??riau ?? l'int??rieur du sol??no??de,
d'o?? il r??sulte que l'inductance d'une bobine est donn??e par:
o?? N est ??lev?? au carr?? en raison de la d??finition de l'inductance.
A noter que, puisque la perm??abilit?? des mat??riaux ferromagn??tiques avec des changements de flux magn??tique appliqu??, l'inductance d'une bobine avec un noyau ferromagn??tique varie g??n??ralement avec le courant.
Inductance d'une ligne coaxiale
Laissez le conducteur interne ont rayon 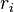 et perm??abilit??
et perm??abilit?? 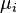 , Que le di??lectrique entre le conducteur int??rieur et ext??rieur ont une perm??abilit??
, Que le di??lectrique entre le conducteur int??rieur et ext??rieur ont une perm??abilit??  , Et laisser le conducteur ext??rieur ont rayon int??rieur
, Et laisser le conducteur ext??rieur ont rayon int??rieur 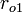 , Rayon ext??rieur
, Rayon ext??rieur  Et la perm??abilit??
Et la perm??abilit??  . Supposons qu'un courant continu
. Supposons qu'un courant continu 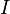 se ??coule dans des directions oppos??es dans les deux conducteurs, avec une densit?? de courant uniforme. Le champ magn??tique g??n??r?? par ces points de courants dans la direction azimutale et est fonction du rayon
se ??coule dans des directions oppos??es dans les deux conducteurs, avec une densit?? de courant uniforme. Le champ magn??tique g??n??r?? par ces points de courants dans la direction azimutale et est fonction du rayon  ; elle peut ??tre calcul??e en utilisant La loi d'Amp??re:
; elle peut ??tre calcul??e en utilisant La loi d'Amp??re:
Le flux par longueur  dans la r??gion entre les conducteurs peut ??tre calcul??e en tra??ant une surface contenant l'axe:
dans la r??gion entre les conducteurs peut ??tre calcul??e en tra??ant une surface contenant l'axe:
A l'int??rieur des conducteurs, L peut ??tre calcul??e en ??galant l'??nergie stock??e dans une inductance,  , Avec l'??nergie stock??e dans le champ magn??tique:
, Avec l'??nergie stock??e dans le champ magn??tique:
Pour une g??om??trie cylindrique sans  d??pendance, l'??nergie par unit?? de longueur est
d??pendance, l'??nergie par unit?? de longueur est
o??  est l'inductance par unit?? de longueur. Pour le conducteur interne, l'int??grale sur la main-c??t?? droit est
est l'inductance par unit?? de longueur. Pour le conducteur interne, l'int??grale sur la main-c??t?? droit est  ; pour le conducteur ext??rieur ce est
; pour le conducteur ext??rieur ce est 
La r??solution de  et en additionnant les termes de chaque r??gion donne ensemble une inductance totale par unit?? de longueur de:
et en additionnant les termes de chaque r??gion donne ensemble une inductance totale par unit?? de longueur de:
Cependant, pour une application typique de ligne coaxiale nous sommes int??ress??s ?? passer des signaux (non-DC) ?? des fr??quences pour lesquelles l'r??sistif effet de peau ne peut ??tre n??glig??e. Dans la plupart des cas, les termes de conducteurs int??rieurs et ext??rieurs sont n??gligeables, auquel cas on peut rapprocher
Phasor analyse des circuits et de l'imp??dance
Utilisation phaseurs, l'??quivalent imp??dance d'une inductance est donn??e par:
o??
- j est l' unit?? imaginaire ,
- L est l'inductance,
- ω = 2 ??? f est la fr??quence angulaire,
- f est la fr??quence et
- ωL = X L est la inductive r??actance.
Inductance non lin??aire
De nombreux inducteurs font appel ?? des mat??riaux magn??tiques . Ces mat??riaux sur une large gamme assez pr??sentent une perm??abilit?? non lin??aire avec des effets tels que saturation. Ceci fait en tournant l'inductance r??sultante une fonction du courant appliqu??. La loi de Faraday, mais d??tient toujours l'inductance est ambigu?? et est diff??rent si vous calculez les param??tres du circuit ou flux magn??tiques.
L'inductance s??cant ou grande-signal est utilis?? dans les calculs de flux. Il est d??fini comme:
L'inductance diff??rentielle ou en petits signaux, d'autre part, est utilis??e dans le calcul de tension. Il est d??fini comme:
La tension de circuit pour un inducteur non lin??aire est obtenu par l'interm??diaire de l'inductance diff??rentiel comme indiqu?? par la loi de Faraday et le r??gle de cha??ne de calcul.
Il existe des d??finitions similaires pour inductances mutuelles non lin??aires.




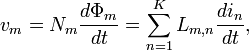

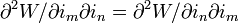


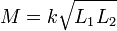
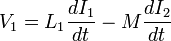




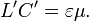

 W << 1
W << 1 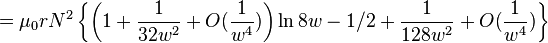 W 1 >>
W 1 >>