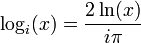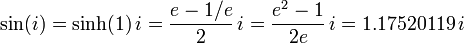Unit?? imaginaire
Contexte des ??coles Wikip??dia
Arrangeant une s??lection Wikipedia pour les ??coles dans le monde en d??veloppement sans internet ??tait une initiative de SOS Enfants. Le parrainage d'enfants aide les enfants un par un http://www.sponsor-a-child.org.uk/ .
En math??matiques, la physique et l'ing??nierie, l'unit?? imaginaire est not??e 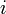 ou du latin
ou du latin  ou grec iota (voir notations alternatives ci-dessous). Il permet au nombre r??el syst??me,
ou grec iota (voir notations alternatives ci-dessous). Il permet au nombre r??el syst??me, 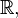 ??tre ??tendu ?? l' nombre complexe syst??me,
??tre ??tendu ?? l' nombre complexe syst??me, 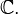 Sa d??finition pr??cise d??pend de la m??thode particuli??re de l'extension.
Sa d??finition pr??cise d??pend de la m??thode particuli??re de l'extension.
La principale motivation de cette extension est le fait que chaque ??quation polynomiale ?? coefficients r??els  a une solution dans les nombres r??els. En particulier, l'??quation
a une solution dans les nombres r??els. En particulier, l'??quation  n'a pas de solution r??elle (voir "D??finition", ci-dessous). Cependant, si nous permettons nombres complexes que des solutions, alors cette ??quation, et en fait chaque ??quation polynomiale
n'a pas de solution r??elle (voir "D??finition", ci-dessous). Cependant, si nous permettons nombres complexes que des solutions, alors cette ??quation, et en fait chaque ??quation polynomiale  ne avoir une solution. (Voir cl??ture alg??brique et th??or??me fondamental de l'alg??bre.)
ne avoir une solution. (Voir cl??ture alg??brique et th??or??me fondamental de l'alg??bre.)
Pour une histoire de l'unit?? imaginaire, voir l'histoire des nombres complexes .
L'unit?? imaginaire est souvent vaguement appel??e la "racine carr??e de n??gatif?? ou la ??racine carr??e de moins un??, mais voir ci-dessous pour les difficult??s qui peuvent survenir d'une utilisation na??ve de cette id??e.
D??finition
Par d??finition, l'unit?? imaginaire  est une solution (de deux) de l' ??quation quadratique
est une solution (de deux) de l' ??quation quadratique
ou de fa??on ??quivalente
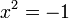 .
.
Comme il n'y a pas de nombre r??el qui produit un nombre r??el n??gatif au carr??, nous imaginons un tel nombre et lui assignons le symbole i. Il est important de r??aliser, cependant, que i est ainsi d??fini une construction math??matique que les nombres r??els, en d??pit de son nom et d'??tre moins imm??diatement intuitive formelle.
Op??rations num??riques r??el peuvent ??tre ??tendus ?? des nombres imaginaires complexes et en traitant i comme une quantit?? inconnue lors de la manipulation d'une expression, puis en utilisant la d??finition de remplacer toutes les occurrences de deux avec i -1. Puissances sup??rieures int??grante de  peut ??galement ??tre remplac?? par - i, 1,
peut ??galement ??tre remplac?? par - i, 1,  Ou -1:
Ou -1:
 et -
et - 
??tre un polyn??me du second degr?? sans multiples racine r??elle, l'??quation ci-dessus a deux solutions distinctes qui sont ??galement valides et qui se trouvent ??tre additif et inverses multiplicatifs de l'autre. Plus pr??cis??ment, une fois une solution  de l'??quation a ??t?? fix??, la valeur -
de l'??quation a ??t?? fix??, la valeur -  (Qui ne est pas ??gal ??
(Qui ne est pas ??gal ??  ) Est aussi une solution. Etant donn?? que l'??quation est la seule d??finition de
) Est aussi une solution. Etant donn?? que l'??quation est la seule d??finition de  Il semble que la d??finition est ambigu?? (plus pr??cis??ment, pas bien d??finie). Toutefois, aucune ambigu??t?? r??sulte aussi longtemps que l'une des solutions est choisi et fix?? comme "positif
Il semble que la d??finition est ambigu?? (plus pr??cis??ment, pas bien d??finie). Toutefois, aucune ambigu??t?? r??sulte aussi longtemps que l'une des solutions est choisi et fix?? comme "positif  . "Ce est parce que, bien que -
. "Ce est parce que, bien que -  et
et  ne sont pas quantitativement ??quivalent (ils sont n??gatifs de l'autre), il ne existe aucune diff??rence qualitative entre
ne sont pas quantitativement ??quivalent (ils sont n??gatifs de l'autre), il ne existe aucune diff??rence qualitative entre  et -
et -  (Qui ne peut ??tre dit pour -1 et +1). Les deux nombres imaginaires ont ??gale pr??tention d'??tre le nombre dont le carr?? est -1. Si tous les manuels de math??matiques et litt??rature publi??e r??f??rant ?? nombres imaginaires ou complexes ont ??t?? r????crit avec -
(Qui ne peut ??tre dit pour -1 et +1). Les deux nombres imaginaires ont ??gale pr??tention d'??tre le nombre dont le carr?? est -1. Si tous les manuels de math??matiques et litt??rature publi??e r??f??rant ?? nombres imaginaires ou complexes ont ??t?? r????crit avec -  remplacer toutes les occurrences de +
remplacer toutes les occurrences de +  (Et donc chaque occurrence de -
(Et donc chaque occurrence de -  remplac?? par - (-
remplac?? par - (-  ) = +
) = +  ), Tous les faits et th??or??mes continueraient d'??tre ??quivalente valide. La distinction entre les deux racines
), Tous les faits et th??or??mes continueraient d'??tre ??quivalente valide. La distinction entre les deux racines  de
de  l'un d'eux comme ??positif?? est purement une relique de notation; ni racine peut ??tre dit pour ??tre plus primaire ou fondamentale que l'autre.
l'un d'eux comme ??positif?? est purement une relique de notation; ni racine peut ??tre dit pour ??tre plus primaire ou fondamentale que l'autre.
La question peut ??tre subtile. L'explication la plus pr??cise est-??-dire que, bien que le complexe champ, d??fini comme R [X] / (X 2 + 1), (voir nombre complexe ) est unique jusqu'?? isomorphisme, il ne est pas unique ?? un unique isomorphisme - il ya exactement deux automorphismes de terrain de R [X] / (X 2 + 1), l'identit?? et l'automorphisme envoyant X - X. (Ce ne sont pas les automorphismes seulement sur le terrain de C, mais sont les seuls automorphismes de terrain de C qui maintiennent chaque nombre r??el fixe.) Voir nombre complexe , conjugaison complexe, automorphisme champ, et Groupe de Galois.
Un probl??me similaire se pose si les nombres complexes sont interpr??t??s comme deux ?? 2 r??els matrices (voir nombre complexe ), car alors la fois
et
des solutions ?? l'??quation matricielle
 .
.
Dans ce cas, l'ambigu??t?? r??sulte du choix g??om??trique dont "direction" autour de la cercle unit?? est la rotation ??positif??. Une explication plus pr??cise est-??-dire que le groupe d'automorphismes de la groupe sp??cial orthogonal SO (2, R) a exactement deux ??l??ments - l'identit?? et l'automorphisme qui ??change "CW" (dans le sens horaire) et les rotations "gauche" (sens anti-horaire). Voir groupe orthogonal.
Toutes ces ambigu??t??s peuvent ??tre r??solus par l'adoption d'une plus rigoureuse d??finition de nombre complexe , et explicitement choisissant l'une des solutions de l'??quation pour l'unit?? imaginaire. Par exemple, la paire ordonn??e (0, 1), dans la construction habituelle des nombres complexes avec des vecteurs bidimensionnels.
L'utilisation appropri??e
L'unit?? imaginaire est parfois ??crit  dans des contextes de math??matiques avanc??es (ainsi que dans les textes populaires les moins avanc??s); Cependant, un grand soin doit ??tre pris lors de la manipulation des formules impliquant radicaux. La notation est r??serv?? soit pour la principale racine carr??e fonction, qui est d??finie uniquement pour de vrai
dans des contextes de math??matiques avanc??es (ainsi que dans les textes populaires les moins avanc??s); Cependant, un grand soin doit ??tre pris lors de la manipulation des formules impliquant radicaux. La notation est r??serv?? soit pour la principale racine carr??e fonction, qui est d??finie uniquement pour de vrai  ≥ 0, ou pour la branche principale de la fonction complexe de la racine carr??e. Tenter d'appliquer les r??gles de calcul de la principale (r??el) fonction de la racine carr??e de manipuler la branche principale de la fonction complexe de la racine carr??e va produire de faux r??sultats:
≥ 0, ou pour la branche principale de la fonction complexe de la racine carr??e. Tenter d'appliquer les r??gles de calcul de la principale (r??el) fonction de la racine carr??e de manipuler la branche principale de la fonction complexe de la racine carr??e va produire de faux r??sultats:
 (Incorrect)
(Incorrect)
La r??gle de calcul
est uniquement valable pour les valeurs r??elles, non n??gatifs de  et
et 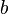 .
.
Pour une discussion plus approfondie de ce ph??nom??ne, voir la racine carr??e et branche.
Pour ??viter de faire de telles erreurs lors de la manipulation des nombres complexes, une strat??gie est de ne jamais utiliser un nombre n??gatif sous un signe de racine carr??e. Par exemple, plut??t que d'??crire des expressions comme 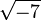 , On devrait ??crire
, On devrait ??crire  ?? la place. Ce est l'usage pour lequel l'unit?? imaginaire a ??t?? cr????.
?? la place. Ce est l'usage pour lequel l'unit?? imaginaire a ??t?? cr????.
Racine carr??e de l'unit?? imaginaire
On pourrait supposer que un autre ensemble de nombres imaginaires doivent ??tre invent?? pour tenir compte de la racine carr??e de i. Cependant ce ne est pas n??cessaire, car il peut ??tre exprim?? (quoique assez mal - voir ci-dessus) que l'un des deux nombres complexes:
Cela peut ??tre d??montr?? pour ??tre valide ?? partir de:
Pouvoirs du 
Les pouvoirs de  r??p??ter dans un cycle:
r??p??ter dans un cycle:
Ceci peut ??tre exprim?? par le sch??ma suivant o?? n est un nombre entier:
Cela conduit ?? la conclusion que
i et la formule d'Euler
La formule d'Euler est
 ,
,
o?? x est un nombre r??el. La formule peut ??galement ??tre prolong?? pour x analytique complexe.
En substituant  rendements
rendements
et on arrive ?? l'??l??gant identit?? d'Euler :
 .
.
Cette ??quation remarquablement simple concerne cinq importantes quantit??s math??matiques (0, 1, π, e, i) et par le biais des op??rations de base de plus, la multiplication et exponentiation.
Exemple
Remplacement de  o?? N est un nombre entier arbitraire, produit
o?? N est un nombre entier arbitraire, produit
Ou, ce qui soul??ve de chaque c??t?? de la puissance  ,
,
ou
 ,
,
ce qui montre que 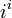 a un nombre infini d'??l??ments sous la forme de
a un nombre infini d'??l??ments sous la forme de
o?? N est un entier quelconque. Cette valeur r??elle bien r??el ne est pas uniquement d??termin??e. La raison en est que la logarithme complexe est multipliez-??valu??.
Op??rations avec i
De nombreuses op??rations math??matiques qui peuvent ??tre r??alis??es avec des nombres r??els peuvent ??galement ??tre effectu??s avec  , Comme exponentation, racines, logarithmes et les fonctions trigonom??triques.
, Comme exponentation, racines, logarithmes et les fonctions trigonom??triques.
Un nombre ??lev?? ?? la 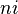 puissance est:
puissance est:
Le 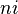 e racine d'un nombre est:
e racine d'un nombre est:
Le connecter la base i d'un nombre est:
Le cosinus de  est un nombre r??el:
est un nombre r??el:
Et le sinus de  est imaginaire:
est imaginaire:
Notations alternatifs
- En g??nie ??lectrique champs et connexes, l'unit?? imaginaire est souvent ??crit
 pour ??viter toute confusion avec courant ??lectrique en fonction du temps, traditionnellement d??sign?? par
pour ??viter toute confusion avec courant ??lectrique en fonction du temps, traditionnellement d??sign?? par  ou tout simplement
ou tout simplement  Le langage de programmation Python utilise ??galement j pour d??signer l'unit?? imaginaire, tandis que dans Matlab, les deux notations i et j sont associ??s ?? l'unit?? imaginaire.
Le langage de programmation Python utilise ??galement j pour d??signer l'unit?? imaginaire, tandis que dans Matlab, les deux notations i et j sont associ??s ?? l'unit?? imaginaire. - Quelques pr??cautions suppl??mentaires doivent ??tre prises dans certains manuels qui d??finissent j = - i, en particulier ?? ondes progressives (par exemple un droit voyager onde plane dans la direction x
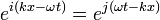 ).
). - Certains textes utilisent la lettre grecque iota (ι) pour ??crire l'unit?? imaginaire pour ??viter toute confusion. Par exemple: Biquaternion.
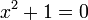

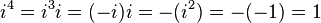



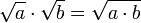

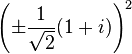

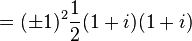



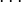



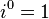

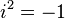


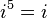

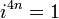







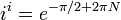

![! \ \ \ Sqrt [ni] {x} = \ cos (\ ln (\ sqrt [n] {x})) - i \ sin (\ ln (\ sqrt [n] {x}))](../../images/218/21805.png)