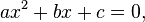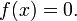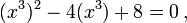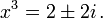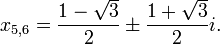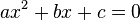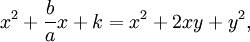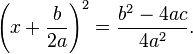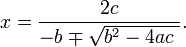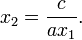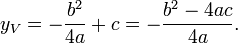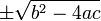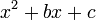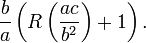??quation quadratique

Renseignements g??n??raux

SOS Enfants a essay?? de rendre le contenu plus accessible Wikipedia par cette s??lection des ??coles. Tous les enfants disponibles pour le parrainage de SOS Enfants des enfants sont pris en charge dans une maison de famille pr??s de la charit??. Lire la suite ...

En math??matiques , une ??quation quadratique est un polyn??me ??quation de la seconde degr??. La forme g??n??rale est

$ax ^ 2 + bx + c = 0, \, \!$

o?? a ≠ 0. (Pour a = 0, l'??quation devient une ??quation lin??aire ).

Les lettres a, b et c sont appel??s : coefficients du coefficient quadratique a est le coefficient de 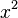$x ^ 2$ , Le coefficient lin??aire b est le coefficient de x, et c est la coefficient constant, aussi appel?? le terme libre ou terme constant.

??quations du second degr?? sont appel??s quadratique parce carr?? est latine pour "carr??"; dans le premier terme est la variable carr??.

Parcelles de r??elle -??valu??es quadratique fonction ax ² + bx + c, variant chaque coefficient s??par??ment

Formule quadratique

Une ??quation quadratique r??els ou complexes coefficients a deux solutions (pas n??cessairement distinctes), appel??s racines, qui peut ??tre r??el ou complexe, ??tant donn?? par la formule quadratique:

$x = \ frac {-b \ h \ sqrt {b ^ 2-4ac}} {} 2a,$

o?? le symbole "??" indique que les deux

$x_ + = \ frac {-b + \ sqrt {b ^ 2-4ac}} {} 2a$

$\ X_- = \ frac {-b - \ sqrt {b ^ 2-4ac}} {} 2a$

sont des solutions.

Autrement dit, ?? de la plus ou moins 'des moyens que les possibilit??s de l'??quation.

Discriminant

Exemple de signes discriminants
■ <0: x ² + _^1/2
■ = 0: - _^4/3 x ² + _^4/3 x - _^1/3
■> 0: _^3/2 x ² + _^1/2 x - _^4/3

Dans la formule ci-dessus, l'expression sous le signe de racine carr??e:

$\ Delta = b ^ 2 - 4ac, \, \!$

est appel?? le discriminant de l'??quation quadratique.

Une ??quation quadratique ?? coefficients r??els peut avoir un ou deux racines r??elles distinctes, ou deux racines complexes distinctes. Dans ce cas, le discriminant d??termine le nombre et la nature des racines. Il ya trois cas:

Si le discriminant est positif, il existe deux racines distinctes, qui sont tous deux des nombres r??els. Pour ??quations du second degr?? avec entiers coefficients, si le discriminant est un carr?? parfait, les racines sont des nombres rationnels , en d'autres cas, ils peuvent ??tre irrationnels quadratiques.
Si le discriminant est nul, il ya exactement une racine distincte, et que la racine est un nombre r??el . Parfois appel?? double racine, sa valeur est:
$x = - \ frac {b} {} 2a. \, \!$
Si le discriminant est n??gatif, il n'y a pas de v??ritables racines. Plut??t, il ya deux (non r??el) distinctes complexes racines, qui sont complexes conjugu??s de l'autre:
$\ Begin {align} x & = \ frac {} {-b 2a} + i \ frac {\ sqrt {4ac - b ^ 2}}} {2a, \\ x & = \ frac {} {-b 2a} - i \ frac {\ sqrt {4ac - b ^ 2}}} {2a, \\ i ^ 2 = -1 &. \ End {align}$

Ainsi, les racines sont distinctes si et seulement si le discriminant est non nul, et les racines sont r??elles si et seulement si le discriminant est non n??gative.

G??om??trie

Pour le fonction quadratique:
f (x) = x ² - x - = 2 (x + 1) (x - 2) d'un r??el variable x, x - les coordonn??es des points o?? la courbe coupe l'axe des x, x = 1 et x = 2, sont le racines de l'??quation quadratique: x ² - x - 2 = 0.

Les racines de l'??quation quadratique

$ax ^ 2 + bx + c = 0, \,$

sont ??galement la z??ros de la fonction quadratique:

$f (x) = ax ^ 2 + bx + c, \,$

??tant donn?? qu'ils sont les valeurs de x pour laquelle

$f (x) = 0 \,$

Si a, b, et c sont des nombres r??els , et le domaine de f est l'ensemble des nombres r??els, les z??ros de f sont exactement les x - coordonn??es des points o?? le graphe touche le axe x.

Il r??sulte de ce qui pr??c??de que, si le discriminant est positif, le graphique touche le axe x en deux points, si z??ro, la touche graphique ?? un moment donn??, et si elle est n??gative, le graphique ne touche pas l'axe des x.

Factorisation quadratique

Le terme

$x - r \,$

est un facteur du polyn??me

$ax ^ 2 + bx + c, \$

si et seulement si r est un racine de l'??quation quadratique

$ax ^ 2 + bx + c = 0. \$

Il r??sulte de la formule quadratique

$ax ^ 2 + bx + c = a \ left (x - \ frac {-b + \ sqrt {b ^ 2-4ac}} {} 2a \ right) \ left (x - \ frac {-b - \ sqrt { b ^ 2-4ac}} {2a} \ droite).$

Dans le cas particulier o?? le quadratique a une seule racine distincte (ce est ?? dire le discriminant est nul), le polyn??me quadratique peut ??tre factoris?? comme

$ax ^ 2 + bx + c = a \ left (x + \ frac {b} {} 2a \ right) ^ 2. \, \!$

Application aux ??quations de degr?? sup??rieur

Certaines ??quations de degr?? sup??rieur peuvent ??tre mis en forme quadratique et r??solus de cette fa??on. Par exemple, l'??quation 6-degr?? en x:

$x ^ 6 - 4x ^ 3 + 8 = 0 \,$

peut ??tre r????crite comme:

$(X ^ 3) ^ 2-4 (x ^ 3) + 8 = 0 \ ,,$

ou, de fa??on ??quivalente, comme une ??quation quadratique dans une nouvelle variable u:

$u ^ 2 - 4u + 8 = 0, \,$

o??

$u = x ^ 3. \,$

R??soudre l'??quation quadratique pour les r??sultats de U dans les deux solutions:

$u = 2 \ h 2i.$

Ainsi

$x ^ 3 = 2 \ h 2i \ ,.$

Concentrant sur la recherche les trois racines de cube

- Les trois autres solutions pour x sera leur conjugu??s complexes - r????criture de la droite ?? l'aide La formule d'Euler:

$x ^ 3 = 2 ^ {\ frac {3} {2}} e ^ {\ frac {1} {4} \ pi} i = 2 ^ {\ frac {3} {2}} e ^ {\ frac { 8k + 1} {4} \ pi i} \,$

(Depuis e ^{2 k π i} = 1), donne les trois solutions:

$x = 2 ^ {\ frac {1} {2}} e ^ {\ frac {1} 8k + {12} \ pi i} \ ,, ~ k = 0, 1, 2 \ ,.$

En utilisant ?? nouveau la formule de Euler avec des identit??s trigonom??triques telles que cos (π / 12) =

, Et en ajoutant les conjugu??s complexes, donne la collection compl??te de solutions que:

$x_ {1,2} = -1 \ h i, \,$

$x_ {3,4} = \ frac {1 + \ sqrt {3}} {2} \ h \ frac {1 - \ sqrt {3}} {2} i \,$

$x_ {5,6} = \ frac. {1 - \ sqrt {3}} {2} \ h \ frac {1 + \ sqrt {3}} {2} i \,$

Histoire

Les Babyloniens, le plus t??t 1800 BC (affich?? sur Old babylonienne tablettes d'argile) pourraient r??soudre une paire d'??quations simultan??es de la forme:

$x + y = p, \ \ xy = q \$

qui sont ??quivalentes ?? l'??quation:

$\ X ^ 2 + q = px$

La paire originale des ??quations ont ??t?? r??solu comme suit:

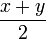
Forme $\ Frac {x + y} {2}$
Forme $\ Left (\ frac {x + y} {2} \ right) ^ 2$
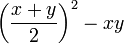
Forme $\ Left (\ frac {x + y} {2} \ right) ^ 2 - xy$
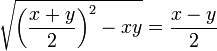
Forme $\ Sqrt {\ left (\ frac {x + y} {2} \ right) ^ 2 - xy} = \ frac {xy} {2}$
Trouver $x, \ y$ par examen des valeurs dans (1) et (4).

Dans le Sulba soutras dans ancienne vers l'Inde 8e si??cle avant notre ??re ??quations du second degr?? de la forme ax ² = c et ax + bx ² = c ont ??t?? explor??s en utilisant des m??thodes g??om??triques. Math??maticiens babyloniens de circa 400 BCE et Math??maticiens chinois de circa 200 BCE a utilis?? la m??thode de compl??tant le carr?? de r??soudre des ??quations du second degr?? avec racines positives, mais ne avait pas de formule g??n??rale. Euclide , le math??maticien grec, produit une m??thode g??om??trique plus abstrait autour 300 BCE.

En 628 CE, Brahmagupta a donn?? la premi??re solution explicite (bien que pas encore tout ?? fait g??n??ral) de l'??quation quadratique:

$\ Ax ^ 2 + bx = c$

Pour le nombre absolu multipli?? par quatre fois la [coefficient de la] carr??, ajouter le carr?? de la [coefficient de la] ?? moyen terme; la racine carr??e de la m??me, moins le [coefficient de la] moyen terme, ??tant divis?? par deux fois le [coefficient de la] place est la valeur. (Brahmasphutasiddhanta (traduction Colebrook, 1817, ?? la page 346)

Ceci est ??quivalent ??:

$x = \ frac {\ sqrt {4ac + b ^ 2} -b} {} 2a.$

Le Bakhshali manuscrit dat?? avoir ??t?? ??crit en Inde dans le 7??me si??cle CE contenait une formule alg??brique pour r??soudre des ??quations du second degr??, ainsi que quadratique ??quations ind??termin??es (?? l'origine du type de hache / c = y). Mohammad bin Musa Al-kwarismi ( Perse , 9??me si??cle ) ont d??velopp?? un ensemble de formules qui ont travaill?? pour des solutions positives. Son travail a ??t?? bas?? sur Brahmagupta. Abraham bar Hiyya Ha-Nasi (??galement connu sous le Latine nom Savasorda) introduit la solution compl??te pour l'Europe dans son livre Liber embadorum dans le 12??me si??cle . Bhāskara II ( 1114- 1185), une indienne math??maticien - astronome, a donn?? la premi??re solution g??n??rale de l'??quation quadratique avec deux racines.

L'??criture du math??maticien chinois Yang Hui ( 1238- 1298 AD) repr??sente la premi??re dans laquelle ??quations du second degr?? ?? coefficients n??gatifs de ??x?? apparaissent, bien qu'il attribue cela au plus t??t Liu Yi.

D??rivation

La formule quadratique peut ??tre obtenue par le proc??d?? de compl??tant le carr??, afin de rendre l'utilisation de l'identit?? alg??brique:

$x ^ 2 + 2xy + y ^ 2 = (x + y) 2 ^. \, \!$

Divisant l'??quation quadratique

$ax ^ 2 + bx + c = 0 \, \!$

par un (qui est permis, car un est non nul), donne:

$x ^ 2 + \ frac {b} {a} x + \ frac {c} {a} = 0, \, \!$

$x ^ 2 + \ frac {b} {a} x = - \ frac {c} {a} \ qquad (1)$

L'??quation quadratique est maintenant dans une forme dans laquelle la m??thode de l'ach??vement du carr?? peut ??tre appliqu??e. Pour "compl??ter le carr??" est de trouver une certaine constante k telle que

$x ^ 2 + \ frac {b} {a} x + k = x ^ 2 + 2xy + y ^ 2, \, \!$

pour un autre y constante. Pour que ces ??quations pour ??tre vrai,

$\ Frac {b} {a} = 2y \!$

$y = \ frac {b} {2a} \, \!$

$k = y ^ 2, \, \!$

ainsi

$k = \ frac {b ^ 2} {4a ^ 2}. \, \!$

Ajout de cette constante de l'??quation (1) produit

$x ^ 2 + \ frac {b} {a} x + \ frac {b ^ 2} {4a ^ 2} = - \ frac {c} {a} + \ frac {b ^ 2} {4a ^ 2} \. , \!$

Le c??t?? gauche est maintenant carr?? parfait parce

$x ^ 2 + \ frac {b} {a} x + \ frac {b ^ 2} {4a ^ 2} = \ left (x + \ frac {b} {} 2a \ right) ^ 2$

Le c??t?? droit peut ??tre ??crit comme une seule fraction, avec un d??nominateur commun 4 ^2. Cela donne

$\ Left (x + \ frac {b} {} 2a \ right) ^ 2 = \ frac {b ^ 2-4ac} {4a ^ 2}.$

Prenant la racine carr??e des deux c??t??s rendements

$\ Left | x + \ frac {b} {} 2a \ right | = \ frac {\ sqrt {b ^ 2-4ac \}} {| 2a |} \ Rightarrow x + \ frac {b} {} 2a = \ h \ frac {\ sqrt {b ^ 2-4ac \ {}}} 2a.$

Isolement de x, donne

$x = - \ frac {b} {2a} \ h \ frac {\ sqrt {b ^ 2-4ac \ {}}} = 2a \ frac {-b \ h \ sqrt {b ^ 2-4ac \}} { 2a}.$

Formule de rechange

Dans certaines situations, il est pr??f??rable d'exprimer les racines dans une forme alternative.

$x = \ frac {} {2c - b \ mp \ sqrt {b ^ 2-4ac \}}.$

Cette alternative n??cessite c ??tre diff??rent de z??ro; pour, si c est ??gal ?? z??ro, la formule donne correctement z??ro comme une racine, mais ne donne aucune seconde racine, non nul. Au lieu de cela, l'un des deux choix pour un produit ∓ division par z??ro, ce qui ne est pas d??finie.

Les racines sont les m??mes quel que soit l'expression que nous utilisons; l'autre forme est simplement une variation alg??brique de la forme commune:

$\ Begin {align} \ frac {-b + \ sqrt {b ^ 2-4ac \}} {} & 2a {} = \ frac {-b + \ sqrt {b ^ 2-4ac \}} {2a} \ cdot \ frac {-b - \ sqrt {b ^ 2-4ac \}} {- b - \ sqrt {b ^ 2-4ac \}} \\ & {} = \ frac {} {4ac 2a \ gauche (- b - \ sqrt {b ^ 2-4ac} \ right)} \\ & {} = \ frac {} {2c - b - \ sqrt {b ^ 2-4ac \}}. \ End {align}$

La formule de remplacement peut r??duire la perte de pr??cision dans l'??valuation num??rique des racines, qui peut ??tre un probl??me si l'une des racines est beaucoup plus petit que l'autre en valeur absolue. Le probl??me de c pouvant ??tre z??ro peut ??tre ??vit?? en utilisant une approche mixte:

$x_1 = \ frac {-b - \ sgn b \, \ sqrt {b ^ 2-4ac}} {} 2a,$

$x_2 = \ frac {c} {} ax_1.$

Ici sgn d??signe la fonction signer.

Mise en ??uvre en virgule flottante

Une attention point de la mise en ??uvre informatique flottante diff??re un peu des deux formes pour produire un r??sultat robuste. En supposant que le discriminant, b ² -4 ac, est positif et b est non nul, le code sera quelque chose comme ce qui suit.

$t: = - \ tfrac12 \ big (b + \ SGN (b) \ sqrt {b ^ 2-4ac} \ big) \, \!$

$r_ {1}: = t / a \, \!$

$r_ {2}: = c / t \, \!$

Voici SGN (b) est le fonction signe, o?? sgn (b) est une si b est positif et -1 si b est n??gatif; son utilisation assure que les quantit??s ajout??es sont de m??me signe, en ??vitant annulation catastrophique. Le calcul de R ₂ utilise le fait que le produit des racines est c / a.

Les formules de Vi??te

Les formules de Vi??te donnent une relation simple entre les racines d'un polyn??me et de ses coefficients. Dans le cas du polyn??me quadratique, ils prennent la forme suivante:

$x_ + + x_- = - \ frac {b} {a}$

$x_ + \ cdot x_- = \ frac {c} {a}.$

La premi??re formule ci-dessus donne une expression commode pour la repr??sentation graphique d'une fonction quadratique. Comme le graphe est sym??trique par rapport ?? une ligne verticale passant par le sommet, quand il ya deux racines r??elles du vertex les coordonn??es X est situ?? ?? la moyenne des racines (ou interceptions). Ainsi, les coordonn??es x du sommet est donn??e par l'expression:

$x_V = \ frac {x_ + + x_-} {2} = - \ frac {b} {} 2a.$

La coordonn??e y peut ??tre obtenue en substituant le r??sultat ci-dessus dans l'??quation quadratique donn??, ce qui donne

$y_V = - \ frac {b ^ 2} {} 4a + c = - \ frac {b ^ 2 - 4ac} {} 4a.$

G??n??ralisations

La formule et sa d??rivation restent correctes si les coefficients a, b et c sont des nombres complexes , ou plus g??n??ralement des membres de l'une champ dont caract??ristique ne est pas 2. (Dans un corps de caract??ristique 2, l'??l??ment 2 est un z??ro et il est impossible de diviser par elle.)

Le symbole

$\ H \ sqrt {b ^ 2-4ac}$

dans la formule doit ??tre comprise comme ??l'un des deux ??l??ments dont le carr?? est

$b ^ 2-4ac, \,$

si ces ??l??ments existent. Dans certains domaines, certains ??l??ments ne ont pas de racines carr??es et certains ont deux; z??ro seulement a juste une racine carr??e, sauf dans les corps de caract??ristique 2. Notez que m??me si un champ ne contient pas une racine carr??e de un nombre, il ya toujours un quadratique champ d'extension qui fait, de sorte que la formule quadratique fera toujours sens comme une formule dans ce domaine d'extension.

Caract??ristique 2

Dans un corps de caract??ristique 2, la formule quadratique, qui se appuie sur deux ??tant un unit??, ne tient pas. Consid??rons le polyn??me quadratique unitaire

$\ Displaystyle x ^ {2} + bx + c$

sur un corps de caract??ristique 2. Si b = 0, alors la solution r??duit ?? extraire une racine carr??e, de sorte que la solution est

$\ Displaystyle x = \ sqrt {c}$

et notez qu'il n'y a qu'une seule racine depuis

$\ Displaystyle - \ sqrt {c} = - \ sqrt {c} + 2 \ sqrt {c} = \ sqrt {c}.$

En r??sum??,

$\ Displaystyle x ^ {2} + c = (x + \ sqrt {c}) ^ {2}.$

Voir r??sidu quadratique pour plus d'informations sur l'extraction des racines carr??es dans des domaines finis.

Dans le cas o?? b ≠ 0, il existe deux racines distinctes, mais si le polyn??me est irr??ductible, ils ne peuvent ??tre exprim??s en termes de racines carr??es des chiffres dans le champ de coefficient. Au contraire, d??finir la racine R-2 (c) de c ?? une racine du polyn??me x ² + x + c, un ??l??ment de la domaine de fractionnement de ce polyn??me. On v??rifie que R (c) + 1 est ??galement une racine. En termes de l'op??ration 2-root, les deux racines de la (non-unitaire) hache quadratique ² + bx + c sont

$\ Frac {b} {a} R \ gauche (\ frac {} {b ac ^ 2} \ right)$

$\ Frac {b} {a} \ left (R \ gauche (\ frac {} {b ac ^ 2} \ right) 1 \ right).$

Par exemple, Soit A un g??n??rateur multiplicatif du groupe d'unit??s de F _4, le Corps de Galois d'ordre quatre (d'o?? a et a + 1 sont les racines de x ² + x + 1 sur ₄ F). Parce que (a + 1) ² = a, a + 1 est la solution unique de l'??quation quadratique x ² + a = 0. D'autre part, le polyn??me x + ax + 1 est irr??ductible sur F _4, F, mais se s??pare plus de _16, o?? il a les deux racines ab et ab + a, o?? b est une racine de x ² + x + a dans F _16.

Ce est un cas particulier de La th??orie d'Artin-Schreier.

Livre

Vedic Mathematics: Seize simple math??matique formules des V??das, par Swami Sankaracarya (1884-1960), Motilal Banarsidass Indological ??diteurs et des libraires, Varnasi, Inde, 1965; r??imprim?? ?? Delhi, en Inde, 1975, 1978. 367 pages.

R??cup??r?? ?? partir de " http://en.wikipedia.org/w/index.php?title=Quadratic_equation&oldid=199164119 "