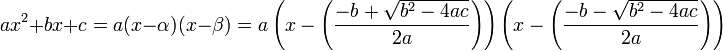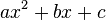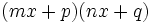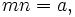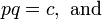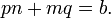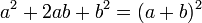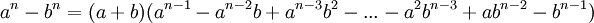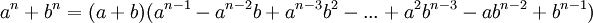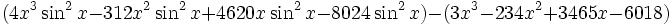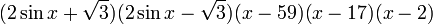Factorisation
Renseignements g??n??raux
SOS Enfants a essay?? de rendre le contenu plus accessible Wikipedia par cette s??lection des ??coles. Pour comparer les organismes de bienfaisance de parrainage ce est le meilleur lien de parrainage .
En math??matiques , factorisation (??galement dans factorisation L'anglais britannique) ou de l'affacturage est la d??composition d'un objet (par exemple, un nombre , un polyn??me ou une matrice ) dans un produit d'autres objets, ou des facteurs qui, lorsqu'ils sont multipli??s ensemble donnent l'original. Par exemple, le nombre 15 facteurs en nombres premiers que 3 ?? 5, et les polyn??mes x 2-4 facteurs que (x - 2) (x + 2). Dans tous les cas, un produit d'objets simples est obtenu.
Le but de l'affacturage est g??n??ralement de r??duire quelque chose ?? "blocs de construction de base," telles que les num??ros ?? nombres premiers, ou polyn??mes ?? polyn??mes irr??ductibles. Affacturage entiers est couvert par le th??or??me fondamental de l'arithm??tique et de affacturage polyn??mes de la th??or??me fondamental de l'alg??bre.
Le contraire de la factorisation est expansion. Ce est le processus de multiplier ainsi les facteurs de recr??er le, original "??largi" polynomiale .
Entier factorisation de grands nombres entiers semble ??tre un probl??me difficile. Il ne existe aucune m??thode connue pour le r??aliser rapidement. Sa complexit?? est la base de la s??curit?? de certaines suppos?? des algorithmes de cryptographie ?? cl?? publique, tels que RSA.
Une matrice peut ??galement ??tre factoris??e en un produit de matrices de types sp??ciaux, pour une application dans laquelle cette forme est pratique. Un exemple majeur de cette utilise un ou orthogonal matrice unitaire, et une matrice triangulaire. Il existe diff??rents types: D??composition QR, LQ, QL, RQ, RZ.
Un autre exemple est la factorisation d'une fonction que la composition d'autres fonctions ayant certaines propri??t??s; par exemple, chaque fonction peut ??tre consid??r??e comme la composition d'un Surjection avec un fonction injective.
Premier factorisation d'un entier
Par le th??or??me fondamental de l'arithm??tique , tous les positifs entier a une situation unique factorisation en nombres premiers. ??tant donn?? un algorithme de factorisation d'entiers, on peut tenir tout entier jusque dans ses constituantes nombres premiers par l'application r??p??t??e de cet algorithme. Pour un tr??s grand nombre, pas efficace algorithme est connu. Pour les plus petits nombres, cependant, il existe une vari??t?? de diff??rents algorithmes qui peuvent ??tre appliqu??s.
Affacturage un polyn??me quadratique
Tout polyn??me quadratique sur les nombres complexes (des polyn??mes de la forme  o??
o??  ,
, 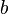 Et
Et  ∈
∈ 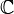 ) Peuvent ??tre pris en compte dans un expression de forme
) Peuvent ??tre pris en compte dans un expression de forme  en utilisant la formule quadratique . La m??thode est la suivante:
en utilisant la formule quadratique . La m??thode est la suivante:
o??  et
et  sont les deux racines du polyn??me, qui se trouvent avec la formule quadratique .
sont les deux racines du polyn??me, qui se trouvent avec la formule quadratique .
Polyn??mes d??composables sur les entiers
Polyn??mes quadratiques peuvent parfois ??tre pris en compte dans deux bin??mes ?? coefficients entiers simples, sans la n??cessit?? d'utiliser la formule quadratique. Dans une ??quation quadratique , ce exposera ses deux racines. La formule
seraient pris en compte dans:
o??
Vous pouvez ensuite d??finir chacune ??gale binomiale ?? z??ro, et ?? r??soudre pour x pour r??v??ler les deux racines. L'affacturage ne implique pas d'autres formules, et est surtout juste quelque chose que vous voyez quand vous arrivez sur une ??quation quadratique.
Prenons, par exemple 2 x 2 - 5 x + 2 = 0. Puisque a = 2 et Mn = a, Mn = 2, ce qui signifie que m et n, on est 1 et l'autre est 2. Maintenant, nous avons (2 x + p) (x + q) = 0. Parce que c = 2 et c = pq, PQ = 2, ce qui signifie que de p et q, on est une et l'autre est 2 ou on est -1 et l'autre est - 2. Une estimation et le contr??le de substituer le 1 et 2, et -1 et -2, en p et q (tout en appliquant pn + mq = b) nous dit que 2 x 2-5 x + 2 = 0 facteurs en (2 x - 1) (x - 2) = 0, nous donnant les racines x = {0,5, 2}
Si un polyn??me ?? coefficients entiers a un discriminant qui est un carr?? parfait, ce polyn??me est factorisable sur les entiers.
Par exemple, regardez le polyn??me 2x 2 + 2x - 12. Si vous remplacez les valeurs de l'expression dans la formule quadratique, le discriminant 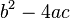 devient 2 ?? 4 f??vrier ?? 2 ?? -12, ce qui ??quivaut ?? 100. 100 est un carr?? parfait, de sorte que le polyn??me 2x 2 + 2x - 12 est factorisable sur les entiers; ses deux facteurs sont, (x - 2) et (x + 3).
devient 2 ?? 4 f??vrier ?? 2 ?? -12, ce qui ??quivaut ?? 100. 100 est un carr?? parfait, de sorte que le polyn??me 2x 2 + 2x - 12 est factorisable sur les entiers; ses deux facteurs sont, (x - 2) et (x + 3).
Maintenant, regardez le polyn??me x 2 + 93x - 2. Son discriminante, 93 2-4 ?? 1 ?? -2, est ??gale ?? 8657, qui ne est pas un carr?? parfait. Donc x 2 + 93x - 2 ne peuvent ??tre factoris?? sur les entiers.
Trin??mes carr?? parfait

Certains quadratiques peuvent ??tre pris en compte dans deux bin??mes identiques. Ces ??quations du second degr?? sont appel??s parfaits trin??mes carr??s. Trin??mes carr??s parfaits peuvent ??tre pris en compte comme suit:
Somme / diff??rence de deux carr??s
Un autre type courant de l'affacturage alg??brique est appel?? diff??rence de deux carr??s. Ce est l'application de la formule
?? tous deux termes, si oui ou non ils sont des carr??s parfaits. Si les deux termes sont soustraites, il suffit d'appliquer la formule. Se ils sont ajout??s, les deux bin??mes obtenus ?? partir de l'affacturage auront chacun un terme imaginaire. Cette formule peut ??tre repr??sent??e comme
 .
.
Par exemple,  peut ??tre pris en compte dans
peut ??tre pris en compte dans 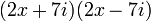 .
.
Affacturage autres polyn??mes
Somme / diff??rence de deux cubes
Une autre formule moins utilis?? mais toujours commune pour l'affacturage est la somme ou la diff??rence de deux cubes. La somme peut ??tre repr??sent?? par
et la diff??rence par
Par exemple, x 3 ?? 10 mars (ou x 3-1000) peut ??tre pris en compte dans (x - 10) (x 2 + 10 + x 100).
Somme / diff??rence de deux nombres ??lev??s ?? la m??me puissance
En g??n??ral,  est un facteur de
est un facteur de  o??
o??  est un entier positif. Alors,
est un entier positif. Alors,
Aussi,  est un facteur de
est un facteur de  o??
o??  est un entier positif pair. Tel que,
est un entier positif pair. Tel que,
De m??me,  est un facteur de
est un facteur de 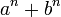 o??
o??  est un entier impair positif. De sorte que,
est un entier impair positif. De sorte que,
Factoring par groupe
Une autre fa??on de tenir compte de certaines ??quations est l'affacturage en regroupant. Ceci est r??alis?? en pla??ant les termes dans une expression en deux ou plusieurs groupes, o?? chaque groupe peut ??tre pris par un proc??d?? connu. Les r??sultats de ces factorisations peuvent parfois ??tre combin??s pour faire une expression encore plus simplifi??e.
Par exemple, supposons que vous aviez l'expression
qui ?? premi??re vue ressemble ?? une expression difficile ?? manier. Une ??tape logique, si vous d??cidez de prendre en compte par le groupe, serait de combiner toutes les expressions avec  et tout cela sans
et tout cela sans  . Ensuite, vous auriez l'expression
. Ensuite, vous auriez l'expression
o?? chacun des deux groupes se factorisent nous donner
Cela peut ??tre encore simplifi??e en
quand peut alors ??tre pris en compte dans
et enfin
qui est l'expression sous forme enti??rement pris en compte.
D'autres formules courantes
Il existe de nombreuses formules suppl??mentaires qui peuvent ??tre utilis??s pour tenir compte facilement un polyn??me. Parmi les plus courants sont r??pertori??s ci-dessous.
| Forme d??velopp??e | Forme factoris??e |
|---|---|
 |  |
 | 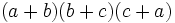 |
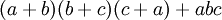 | 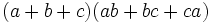 |
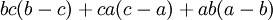 | 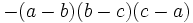 |
 | 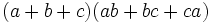 |
 | 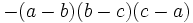 |
 | 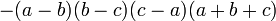 |
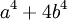 ( Sophie Germain de l'identit??) ( Sophie Germain de l'identit??) |  |
Factoring en logique math??matique
En la logique math??matique et automatis??e de th??or??me, l'affacturage est la technique de d??river une seule, plus sp??cifique atome d'une disjonction des deux plus g??n??rale atomes unifiables. Par exemple, ?? partir de ∀ X, Y: P (x, a) ou P (B, Y), on peut calculer P (b, a).