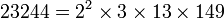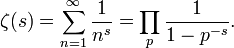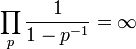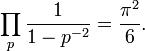Nombre premier

Renseignements g??n??raux

SOS Enfants a essay?? de rendre le contenu plus accessible Wikipedia par cette s??lection des ??coles. Visitez le site Web d'enfants SOS au http://www.soschildren.org/

Ensembles d'entiers base divisibilit??-

Vue d'ensemble	Factorisation Entier Diviseur Diviseur unitaire Fonction diviseur Premier facteur Th??or??me fondamental de l'arithm??tique

Les formes de factorisation	Nombre premier Num??ro Composite Nombre semi-premier num??ro Nombre oblong Nombre sph??nique Num??ro sans Square- Nombre puissant Puissance parfaite Num??ro d'Achille Nombre lisse Nombre r??gulier Chiffre approximatif Nombre inhabituel

Sommes contraints de diviseurs	Nombre parfait Nombre presque parfait Nombre quasi parfait Nombre parfait multiple num??ro de Hemiperfect Nombre hyperparfait Num??ro Superperfect Nombre parfait unitaire Nombre semi-parfait Num??ro Pratique

Avec de nombreux diviseurs	Nombre abondant Nombre abondant Primitive Nombre hautement abondant Nombre superabondant Nombre colossalement abondant Nombre hautement compos?? Nombre hautement compos?? Sup??rieur Nombre ??trange

Relatif ?? s??quences aliquotes	Nombre intouchable Num??ro amiable Nombre sociable Num??ro fianc??e

Autres s??ries	Nombre d??ficient Num??ro bienvenus Num??ro solitaire Nombre sublime Num??ro de diviseur harmonique Nombre frugal Nombre ??quidigital Nombre extravagant

En math??matiques , un nombre premier (ou un premier) est un nombre naturel (plus d'un), qui a exactement deux distincts nombre naturel diviseurs : 1 et lui-m??me. Une infinit?? de nombres premiers existe, comme d??montr?? par Euclid autour 300 BC. Les trente premiers nombres premiers sont:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113
(S??quence A000040 dans OEIS )

Voir la liste des nombres premiers pour une liste plus longue. Le num??ro un est, par d??finition, pas un nombre premier; voir la discussion ci-dessous en vertu de primalit?? d'un .

La propri??t?? d'??tre un premier est appel?? primalit??, et le mot Premier est ??galement utilis?? comme un adjectif. Depuis deux est le seul nombre premier, le terme premier impair se r??f??re ?? ne importe quel nombre premier sup??rieur ?? deux.

L'??tude des nombres premiers est partie de la th??orie des nombres , la branche des math??matiques qui englobe l'??tude des nombres naturels. Les nombres premiers ont fait l'objet d'intenses recherches, mais certaines questions fondamentales, telles que le Hypoth??se de Riemann et de la conjecture de Goldbach , ont ??t?? en suspens pendant plus d'un si??cle. Le probl??me de la mod??lisation de la distribution des nombres premiers est un sujet populaire d'investigation pour les th??oriciens des nombres: quand on regarde des num??ros individuels, les nombres premiers semblent ??tre distribu??s de fa??on al??atoire, mais la r??partition "globale" des nombres premiers suit lois bien d??finies.

La notion de nombre premier a ??t?? g??n??ralis?? dans de nombreuses branches diff??rentes des math??matiques.

En la th??orie des anneaux, une branche de l'alg??bre abstraite , le terme ????l??ment principal?? a une signification particuli??re. Ici, une valeur non nulle, non-unit?? d'un ??l??ment annulaire est d??fini pour ??tre premier si chaque fois qu'un divise bc pour les ??l??ments de l'anneau B et C, puis a divise au moins l'un des b ou c. Avec ce sens, l'inverse additif de tout nombre premier est aussi premier. En d'autres termes, lorsque l'on consid??re l'ensemble des nombres entiers comme anneau, -7 est un ??l??ment primordial. Sans autre pr??cision, cependant, "nombre premier" signifie toujours un premier entier positif. Parmi anneaux de complexe entiers alg??briques, Eisenstein amorce, et Nombres premiers gaussiennes peuvent aussi ??tre d'int??r??t.
Dans la th??orie des n??uds , un Premier noeud est un noeud qui ne peut ??tre ??crit comme la somme de n??ud de deux n??uds moins triviaux.

Histoire de nombres premiers

Le Crible d'??ratosth??ne est une simple, ancienne algorithme pour trouver tous les nombres premiers jusqu'?? un entier sp??cifi??. Il est le pr??d??cesseur de la moderne Crible d'Atkin, qui est plus rapide mais plus complexe. Le crible d'Eratosth??ne ??ponyme a ??t?? cr????e dans le 3??me si??cle avant JC par Eratosth??ne, un grec ancien math??maticien .

Il ya des indices dans les dossiers survivants des anciens Egyptiens qu'ils avaient une certaine connaissance des nombres premiers: la Expansions fraction ??gyptiens dans le Papyrus Rhind, par exemple, ont des formes tr??s diff??rentes de nombres premiers et pour les composites. Cependant, les premiers enregistrements de survivants de l'??tude explicite des nombres premiers viennent des Grecs de l'Antiquit?? . ??l??ments d'Euclide (circa 300 BC) contient th??or??mes importants sur les nombres premiers, y compris l'infinit?? de nombres premiers et th??or??me fondamental de l'arithm??tique . Euclide a ??galement montr?? comment construire un nombre parfait d'un Premier de Mersenne. Le Crible d'??ratosth??ne, attribu?? ?? Eratosth??ne, est une m??thode simple pour calculer les nombres premiers, bien que les grands nombres premiers trouv??s aujourd'hui avec les ordinateurs ne sont pas g??n??r??s de cette fa??on.

Apr??s les Grecs, peu se est pass?? avec l'??tude des nombres premiers jusqu'?? ce que le 17??me si??cle. En 1640, Pierre de Fermat a d??clar?? (sans preuve) Le petit th??or??me de Fermat (plus tard prouv?? par Leibniz et Euler ). Un cas particulier du th??or??me de Fermat peut avoir ??t?? connu beaucoup plus t??t par les Chinois. Fermat conjectur?? que tous les num??ros de la forme 2 ^{2 n} + 1 sont premiers (ils sont appel??s Fermat num??ros) et il a v??rifi?? ce jusqu'?? n = 4. Cependant, le lendemain nombre de Fermat 2 ³² 1 est composite (l'un de ses facteurs premiers est de 641), comme Euler d??couvrit plus tard, et en fait pas plus loin nombres de Fermat sont connus d'??tre premier. Le moine fran??ais Marin Mersenne regarda premiers de la forme 2 ^p - 1, avec p un nombre premier. Ils s'appellent Nombres premiers de Mersenne dans son honneur.

Le travail d'Euler en th??orie des nombres inclus de nombreux r??sultats sur les nombres premiers. Il a montr?? la s??rie infinie _^1/2 + _^1/3 + _^1/5 + _^1/7 + _^1/11 + ... est divergente. En 1747, il a montr?? que les nombres m??me parfaits sont pr??cis??ment les entiers de la forme 2 ^{p -1} (2 ^p -1) o?? le deuxi??me facteur est un nombre premier de Mersenne. On croit pas nombres parfaits impairs existent, mais il ya encore aucune preuve.

Au d??but du 19??me si??cle, Legendre et Gauss ind??pendamment conjectur?? que x tend vers l'infini, le nombre de nombres premiers jusqu'?? x est asymptotique ?? x / log (x), o?? log (x) est le logarithme naturel de x. Id??es de Riemann dans son document de 1859 sur la fonction zeta esquiss?? un programme qui conduirait ?? une preuve du th??or??me des nombres premiers. Ce sch??ma a ??t?? compl??t?? par Hadamard et de la Vall??e Poussin, qui a prouv?? ind??pendamment th??or??me des nombres premiers en 1896.

Prouver un nombre est premier ne est pas fait (pour un grand nombre) par division de proc??s. Beaucoup de math??maticiens ont travaill?? sur tests de primalit?? pour un grand nombre, souvent limit??s ?? des formes num??riques sp??cifiques. Ceci comprend Le test de P??pin pour nombres de Fermat (1877), Th??or??me de Proth (environ 1 878), le Test de Lucas-Lehmer pour les nombres de Mersenne (origine 1856), et de la g??n??ralisation Test de Lucas-Lehmer. Algorithmes plus r??cents comme APRT-CL, ECPP et AKS travaillent sur un nombre arbitraire mais restent beaucoup plus lent.

Pendant longtemps, les nombres premiers ??taient consid??r??s comme ne ayant aucune application possible ?? l'ext??rieur de math??matiques pures; cela a chang?? dans les ann??es 1970 lorsque les concepts de cryptographie ?? cl?? publique ont ??t?? invent??s, dans lequel les nombres premiers forment la base des premiers algorithmes tels que le Algorithme de cryptage RSA.

Depuis 1951, tous les plus grands nombres premiers connus ont ??t?? trouv??s par les ordinateurs . La recherche de plus en plus grands nombres premiers a suscit?? un int??r??t en dehors des cercles math??matiques. Le Great Internet Mersenne Prime Search et d'autres projets de calcul distribu?? pour trouver grands nombres premiers sont devenus populaires dans les dix ?? quinze derni??res ann??es, tandis que les math??maticiens continuent de lutter avec la th??orie des nombres premiers.

Primalit?? d'un

Jusqu'au 19??me si??cle, la plupart des math??maticiens consid??r?? comme le num??ro 1 un premier, et il ya encore un grand corps de travail math??matique qui est valide malgr?? l'??tiquetage 1 un premier, comme le travail de Stern et Zeisel. Liste de Derrick Lehmer Norman de nombres premiers jusqu'?? 10006721, r??imprim?? aussi tard que 1956 ,, a commenc?? avec une comme son premier premier. Henri Lebesgue est dit ??tre le dernier math??maticien professionnel d'appeler une prime. Le changement de l'??tiquette produit de sorte que le th??or??me fondamental de l'arithm??tique , comme indiqu??, est valide, ce est ?? dire, "chaque num??ro a une unique factorisation en facteurs premiers"

Prime diviseurs

Illustration montrant que 11 est un nombre premier alors que 12 ne est pas.

Le th??or??me fondamental de l'arithm??tique stipule que tout nombre entier positif sup??rieur ?? 1 peut ??tre ??crit comme un produit d'un ou plusieurs nombres premiers d'une mani??re qui est unique, sauf peut-??tre pour la commande des premiers facteurs . Le m??me facteur principal peut se produire plusieurs fois. Primes peut donc ??tre consid??r?? comme les ??blocs de construction de base" des nombres naturels. Par exemple, nous pouvons ??crire

$23244 = 2 ^ 2 \ 3 \ times fois 13 \ 149 fois$

et tout autre factorisation de 23 244 comme le produit de nombres premiers sera identique ?? l'exception de l'ordre des facteurs. Il y a beaucoup de algorithmes de factorisation en nombres premiers pour ce faire dans la pratique pour un plus grand nombre.

L'importance de ce th??or??me est l'une des raisons de l'exclusion de l'une de l'ensemble des nombres premiers. Si une ont ??t?? admis en tant que premier, la d??claration pr??cise du th??or??me serait exiger des qualifications suppl??mentaires.

Propri??t??s de nombres premiers

Lorsque ??crit en base 10 , tous les nombres premiers, sauf deux et cinq fin en 1, 3, 7 ou 9. (num??ros se terminant par 0, 2, 4, 6 ou 8 repr??sentent des multiples de deux et les num??ros se terminant par 0 ou 5 repr??sentent des multiples de 5.)

Si p est un nombre premier et p divise un produit ab des entiers, alors p divise a ou p divise b. Cette proposition a ??t?? prouv?? par Euclide et est connu comme Lemme d'Euclide. Il est utilis?? dans quelques preuves de l'unicit?? de facteurs premiers.

Le anneau Z / n Z (voir arithm??tique modulaire ) est un domaine si et seulement si n est un nombre premier. En d'autres termes: n est premier si et seulement si φ (n) = n - 1.

Si p est premier et un est tout entier, puis un ^p - a est divisible par p ( Le petit th??or??me de Fermat).

Si p est un nombre premier diff??rent de 2 et 5, ¹ / _p est toujours d??cimal p??riodique dont la p??riode est p - 1, ou un diviseur de p - 1. Ceci peut ??tre d??duit directement de Le petit th??or??me de Fermat. ¹ / _p exprim?? ??galement dans q de base (autre que la base 10) a un effet similaire, ?? condition que p ne est pas un facteur premier de q. L'article sur d??cimales r??currentes montre quelques-unes des propri??t??s int??ressantes.

Un entier p> 1 est premier si et seulement si la factorielle (p - 1)! + 1 est divisible par p ( Th??or??me de Wilson). A l'inverse, un nombre entier n> 4 est composite si et seulement si (n - 1)! est divisible par n.

Si n est un nombre entier positif sup??rieur ?? 1, alors il n'y a toujours un nombre premier p avec n <p <2 n ( Le postulat de Bertrand).

Ajout inverses de tous les nombres premiers ensemble des r??sultats dans un divergent s??rie infinie ( la preuve). Plus pr??cis??ment, si S (x) repr??sente la somme des inverses de tous les nombres premiers p, avec p ≤ x, alors S (x) = ln ln x + O (1) pour x → ∞.

Dans chaque progression arithm??tique a, a q +, a + 2 q, a + 3 q, ... o?? les entiers a et q sont positifs premiers entre eux, il existe une infinit?? de nombres premiers ( Th??or??me de la progression arithm??tique).

Le caract??ristique de chaque champ est soit z??ro, soit un nombre premier.

Si G est un fini groupe p et ⁿ est le plus grande puissance du nombre premier p qui divise l'ordre de G, alors G a un sous-groupe d'ordre p ^n. ( Th??or??mes de Sylow.)

Si G est un groupe fini et p est un nombre premier divisant l'ordre de G, alors G contient un ??l??ment d'ordre p. ( Cauchy Th??or??me)

Le nombre premier th??or??me dit que la proportion des nombres premiers de moins de x est asymptotique ?? ¹ / _{x ln} (en d'autres termes, lorsque x devient tr??s grande, la probabilit?? qu'un nombre inf??rieur ?? x est un nombre premier est inversement proportionnelle au nombre de chiffres de x ).

Le Copeland-Erdős constante 0,235711131719232931374143 ..., obtenu par concat??nation des nombres premiers en base dix , est connu pour ??tre un nombre irrationnel .

La valeur de la Fonction z??ta de Riemann ?? chaque point dans le plan complexe est donn?? comme un prolongement m??romorphe d'une fonction, d??finie par un produit sur l'ensemble de tous les nombres premiers pour Re (s)> 1:

$\ Zeta (s) = \ sum_ {n = 1} ^ \ infin \ frac {1} {n ^ s} = \ prod_ {p} \ frac {1} {1-p ^ {- s}}.$

??valuer cette identit?? ?? diff??rents entiers fournit un nombre infini de produits au cours des nombres premiers dont les valeurs peuvent ??tre calcul??s, les deux premiers ??tant

$\ Prod_ {p} \ frac {1} {1-p ^ {- 1}} = \ infty$

$\ Prod_ {p} \ frac {1} {1-p ^ {- 2}} = \ frac {\ pi ^ 2} {6}.$

Si p> 1, le polyn??me $x ^ {p-1} + x ^ {p-2} + \ cdots + 1$ est irr??ductible sur Z / p Z si et seulement si p est premier.

Classification des nombres premiers

Deux fa??ons de classer les nombres premiers, la classe et la classe n + n -, ont ??t?? ??tudi??s par Paul Erdős et John Selfridge.

D??termination de la classe n + d'un nombre premier p implique regardant le plus grand facteur premier de p + 1. Si ce plus grand facteur premier est 2 ou 3, alors p est la classe 1+. Mais si ce grand facteur premier est un autre premier q, alors la classe n + p est un de plus que la classe n + q. S??quences A005105 travers A005108 liste classe 1+ ?? travers les nombres premiers de la classe.

La classe n - est presque la m??me que la classe n +, sauf que la factorisation de p - 1 est regard?? ?? la place.

Le nombre des nombres premiers

Il existe une infinit?? de nombres premiers

La plus ancienne preuve de la d??claration qu'il ya infiniment de nombres premiers est donn??e par le math??maticien grec Euclide dans ses ??l??ments (Livre IX, Proposition 20). Euclid indique le r??sultat comme "il ya plus de ne importe quel nombre [finis] donn?? des nombres premiers", et sa preuve est essentiellement la suivante:

Consid??rons un ensemble fini de nombres premiers. Multipliez tous ensemble et ajouter une (voir Nombre d'Euclide). Le nombre obtenu ne est pas divisible par aucun des nombres premiers dans l'ensemble fini nous avons consid??r??, parce divisant par l'un de ces donnerait un reste d'un. Parce que tous les num??ros non-prime peut ??tre d??compos?? en un produit de nombres premiers sous-jacentes, alors soit ce nombre est premier r??sultante elle-m??me, ou se il ya un nombre premier ou nombres premiers dont le nombre r??sultante peut ??tre d??compos??e en, mais ne sont pas dans l'ensemble fini d'origine des nombres premiers. De toute fa??on, il ya au moins un plus de choix qui ne ??tait pas dans l'ensemble fini nous avons commenc?? avec. Cet argument se applique peu importe ce que nous avons commenc?? ensemble fini avec. Donc, il ya plus de primes que ne importe quel nombre fini donn??.

Cet argument pr??c??dente explique pourquoi le produit P de fini de nombres premiers plus 1 doit ??tre divisible par certains Premier pas parmi ces fini de nombres premiers (peut-??tre lui-m??me).

La preuve est parfois formul??e dans un chemin qui m??ne ?? l'??tudiant de conclure que P + 1 doit lui-m??me ??tre premier, et je pense que la preuve d'Euclide dit le produit pr??f??rentiel major?? de 1 est toujours premier. L'exemple simple (2 ?? 3 ?? 5 ?? 7 ?? 11 ?? 13) + 1 = 30 031 = 59 509 ?? (deux nombres premiers) montre que ce ne est pas le cas. En fait, ne importe quel ensemble de nombres premiers qui ne inclut pas deux aura un produit ??trange. Ajout de 1 ?? ce produit sera toujours produire un nombre pair, qui sera divisible par 2 (et donc ne pas ??tre premier).

Autres math??maticiens ont donn?? d'autres preuves. L'un d'eux (en raison d' Euler ) montre que la somme des inverses des nombres premiers diverge. Autre la preuve sur la base Nombres de Fermat a ??t?? donn??e par Goldbach. Kummer est particuli??rement ??l??gant et Harry Furstenberg fournit en utilisant une topologie g??n??rale.

Compter le nombre des nombres premiers en dessous d'un nombre donn??

M??me si le nombre total de nombres premiers est infinie, on pouvait encore se demander ??Environ combien de nombres premiers sont l?? ci-dessous 100 000?", Ou "Quelle est la probabilit?? d'un num??ro ?? 20 chiffres au hasard pour ??tre premier?".

Le Premier comptage fonction π (x) est d??fini comme le nombre de nombres premiers jusqu'?? x. Il ya connus algorithmes pour calculer les valeurs exactes de π (x) plus vite que ce serait possible de calculer chaque premier ?? x. Les valeurs aussi grandes que π (10 ²⁰⁾ peuvent ??tre calcul??s rapidement et avec pr??cision avec les ordinateurs modernes. Ainsi, par exemple, π (100 000) = 9,592, et π (10 ²⁰⁾ = 2.220.819.602.560.918.840.

Pour les plus grandes valeurs de x, au-del?? de la port??e de l'??quipement moderne, le th??or??me des nombres premiers fournit une bonne estimation: π (x) est d'environ x / ln (x). M??me meilleures estimations sont connus.

Lieu de nombres premiers

Trouver nombres premiers

L'ancien Crible d'??ratosth??ne est un moyen simple de calculer tous les nombres premiers jusqu'?? une limite donn??e, en faisant une liste de tous les entiers et ?? plusieurs reprises la suppression des multiples de nombres premiers d??j?? trouv??. Le moderne Crible d'Atkin est plus compliqu??, mais plus rapide lorsqu'il est correctement optimis??.

Dans la pratique, on veut souvent pour v??rifier si un nombre donn?? est premier, plut??t que de g??n??rer une liste de nombres premiers. En outre, il est souvent satisfaisante pour conna??tre la r??ponse avec une forte probabilit?? . Il est possible de v??rifier rapidement si un grand nombre donn?? (disons, jusqu'?? quelques milliers de chiffres) est premier en utilisant probabiliste tests de primalit??. Ces choisissent g??n??ralement un nombre al??atoire appel?? un ??t??moin?? et v??rifier une formule impliquant le t??moin et le premier N potentiel. Apr??s plusieurs it??rations, ils d??clarent que N soit ??certainement composite?? ou ??probablement premier". Certains de ces tests ne sont pas parfaits: il peut y avoir certains nombres compos??s, appel??s pseudopremiers pour le test respective, qui sera d??clar?? ??probablement premier" peu importe ce t??moin est choisi. Cependant, les tests les plus populaires probabilistes ne souffrent pas de cet inconv??nient.

Un proc??d?? pour d??terminer si un nombre est premier est de diviser par tous les nombres premiers inf??rieur ou ??gal ?? la racine carr??e de ce nombre. Si l'une des divisions venus, comme un entier, puis le num??ro d'origine ne est pas un nombre premier. Sinon, ce est un nombre premier. On n'a pas vraiment calculer la racine carr??e; une fois on voit que la quotient est inf??rieur au d??nominateur, on peut arr??ter. Ceci est connu comme division de premi??re instance; ce est le test de primalit?? simple et il devient rapidement impraticable pour tester de grands entiers parce que le nombre de facteurs possibles cro??t de fa??on exponentielle le nombre de chiffres dans les augmentations num??ro ??-??tre-test??s.

tests de primalit??

Un algorithme de test de primalit?? est un algorithme qui teste un certain nombre de primalit??, ?? savoir si le nombre est un nombre premier.

Test de primalit?? AKS
Test de primalit?? de Fermat
Test de Lucas-Lehmer
Test de primalit?? Solovay-Strassen
Test de primalit?? de Miller-Rabin
Courbe elliptique primalit?? proving

Un Premier probable est un entier qui, en vertu d'avoir pass?? un certain test, est consid??r?? comme probablement premier. Nombres premiers probables qui sont en fait composite (tels que Nombres de Carmichael) sont appel??s pseudopremiers.

En 2002, des scientifiques indiens ?? IIT Kanpur d??couvert un nouvel algorithme d??terministe connu sous le nom AKS algorithme. La quantit?? de temps que cela prend algorithme pour v??rifier si un nombre N est premier d??pend d'un fonction polynomiale du nombre de chiffres du N (c. du logarithme de N).

Formules rendement nombres premiers

Il ne est pas connue formule de nombres premiers qui est plus efficace de trouver des nombres premiers que les m??thodes mentionn??es ci-dessus sous la rubrique ??Trouver des nombres premiers".

Il ya un ensemble de ??quations diophantiennes en 9 variables et un param??tre avec la propri??t?? suivante: le param??tre est premier si et seulement si le syst??me d'??quations r??sultant a une solution sur les nombres naturels. Ceci peut ??tre utilis?? pour obtenir une formule simple avec la propri??t?? que toutes ses valeurs positives sont premiers.

Il n'y a pas polynomiale , m??me dans plusieurs variables, qui ne prend que des valeurs de premier ordre. Par exemple, le polyn??me f curieux dans une variable (n) = n ² - n + 41 c??de nombres premiers pour n = 0, ..., 40,43 mais f (41) et f (42) sont composite. Cependant, il ya des polyn??mes en plusieurs variables, dont les valeurs positives que les variables prendre toutes les valeurs enti??res positives sont exactement les nombres premiers.

Une autre formule est bas??e sur le th??or??me de Wilson mentionn?? ci-dessus, et g??n??re le nombre deux plusieurs fois et toutes les autres primes exactement une fois. Il existe d'autres formules similaires qui produisent ??galement des nombres premiers.

Les types particuliers de nombres premiers de formules de nombres premiers

Un nombre premier p est appel?? primorial ou premier-factorielle si elle a la forme p = n # ?? 1 pour un certain nombre n, o?? n # d??signe le produit 2 ?? 3 ?? 5 ?? 7 ?? 11 ?? ... de tous les nombres premiers ≤ n. Un premier est appel?? factorielle si elle est de la forme ! n ?? 1. Les premiers nombres premiers factoriels sont:

n! - 1 est un nombre premier pour n = 3, 4, 6, 7, 12, 14, 30, 32, 33, 38, 94, 166, 324, ... (s??quence A002982 dans OEIS )

n! + 1 est premier pour n = 0, 1, 2, 3, 11, 27, 37, 41, 73, 77, 116, 154, 320, ... (s??quence A002981 dans OEIS )

Le plus grand nombre premier connu est primorial Π (392 113) + 1, trouv?? par Heuer en 2001. Le plus grand nombre premier connu est factorielle 34790! - 1, trouv?? par Marchal, Carmody et Kuosa en 2002. On ne sait pas se il existe une infinit?? de nombres premiers primorial ou factoriels.

Premiers de la forme 2 ^p - 1, o?? p est un nombre premier, sont connus comme Nombres premiers de Mersenne, tandis que les nombres premiers de la forme $2 ^ {2 ^ n + 1}$ sont connus comme Fermat amorce. Nombres premiers p o?? 2 p + 1 est aussi premier sont connus comme Sophie Germain amorce. La liste suivante est d'autres types sp??ciaux de nombres premiers qui viennent de formules:

Wieferich amorce,
Wilson amorce,
Wall-Sun-Sun amorce,
Wolstenholme amorce,
Primes uniques,
Newman-Shanks-Williams amorce (primes NSW),
Smarandache-Wellin amorce,
Wagstaff amorce, et
Supersinguliers nombres premiers.

Certains nombres premiers sont class??s en fonction des propri??t??s de leurs chiffres en d??cimal ou d'autres bases. Par exemple, des nombres dont les chiffres forment un s??quence palindromique sont appel??s palindromiques nombres premiers, et un nombre premier est appel?? Premier truncatable si la suppression successivement le premier chiffre ?? la droite seulement les rendements de nouveaux nombres premiers gauche ou.

Pour une liste des classes sp??ciales de nombres premiers Voir Liste des nombres premiers

La distribution des nombres premiers

La r??partition de l'ensemble des nombres premiers dans la plage de 1 ?? 76 800, de gauche ?? droite et de haut en bas, dans laquelle chaque pixel repr??sente un nombre. Les pixels noirs signifient que nombre est premier et blanc signifie qu'il ne est pas premier.

Le probl??me de la mod??lisation de la distribution des nombres premiers est un sujet populaire d'investigation pour les th??oriciens des nombres. Les nombres premiers sont r??partis entre les nombres naturels d'une mani??re (?? ce jour) impr??visible, mais il ne semble y avoir des lois r??gissant leur comportement. Leonhard Euler comment??

Les math??maticiens ont tent?? en vain de cette journ??e pour d??couvrir un peu d'ordre dans la s??quence des nombres premiers, et nous avons raison de croire que ce est un myst??re dans lequel l'esprit ne sera jamais p??n??trer. (Havil 2003, p. 163)

Paul Erdős dit

Dieu ne peut pas jouer aux d??s avec l'univers, mais quelque chose d'??trange qui se passe avec les nombres premiers. [Se r??f??rant ?? Albert Einstein c??l??bre la conviction de que ??Dieu ne joue pas aux d??s avec l'univers."]

Dans une conf??rence 1975, Don Zagier comment??

Il ya deux faits sur la r??partition des nombres premiers dont je esp??re vous convaincre si massivement qu'ils seront grav??s en permanence dans vos c??urs. La premi??re est que, en d??pit de leur d??finition simple et le r??le que les blocs de construction des nombres naturels, les nombres premiers poussent comme des mauvaises herbes entre les nombres naturels, semblant ob??ir ?? aucune autre loi que celle du hasard, et personne ne peut pr??dire o?? la prochaine va germer. Le deuxi??me fait est encore plus ??tonnant, car il affirme tout le contraire: que les nombres premiers pr??sentent une r??gularit?? ??tonnante, qu'il ya des lois r??gissant leur comportement, et qu'ils ob??issent ?? ces lois avec une pr??cision quasi militaire.

(Havil 2003, p. 171)

Image suppl??mentaires avec 2310 colonnes est li??e ici, la pr??servation des multiples de 2,3,5,7,11 dans les colonnes respectives.

Les ??carts entre les nombres premiers

Soit p _n le n-i??me nombre premier (p-??-dire ₁ = 2, p = ₂ 3, etc.). L'??cart entre la _n g cons??cutive nombres premiers p et _n p _{n + 1} est la diff??rence entre eux, ?? savoir

g _n = p _{n + 1} - P _n.

Nous avons g ₁ = 3-2 = 1, g ₂ = 5-3 = 2, ₃ g = 7-5 = 2, ₄ g = 11-7 = 4, et ainsi de suite. La s??quence (g _n) de premiers espaces a ??t?? largement ??tudi??e.

Pour tout nombre naturel N sup??rieur ?? 1, la s??quence (pour la notation N! Lire factorielle )

N! + 2, N! + 3, ..., N! + N

est une s??quence de N - 1 composites entiers cons??cutifs. Par cons??quent, il existe des ??carts entre les nombres premiers qui sont arbitrairement grand, ?? savoir pour ne importe quel nombre entier naturel N, y est un nombre entier avec n g _n> N. (Choisissez n sorte que p _n est le plus grand nombre premier inf??rieur ?? N! + 2.)

D'autre part, les ??carts se arbitrairement petit en proportion des nombres premiers: le quotient g _n / _n p se approche de z??ro lorsque n tend vers l'infini. Notez ??galement que le conjecture des nombres premiers jumeaux affirme que g _n = 2 pour une infinit?? d'entiers n.

Lieu de la plus grand nombre premier connu

Wikinews a des nouvelles li??es: ??quipe informatique CMSU d??couvre un autre record taille Premier

Wikinews a des nouvelles li??es: L'informatique distribu??e d??couvre plus grand nombre premier connu

Le plus grand nombre premier connu, ?? partir de Ao??t 2007, est 2 ^32582657 - 1 (ce nombre est 9,808,358 chiffres); ce est la 44e connu Premier de Mersenne. M _32582657 a ??t?? trouv?? sur 4 septembre 2006 par Curtis Cooper et Steven Boone, professeurs ?? la Universit?? du Missouri Central (anciennement Central Missouri State University) et les membres d'un effort de collaboration appel?? GIMPS. Avant de trouver le premier, Cooper et Boone ont couru le logiciel GIMPS sur un pic de 700 ordinateurs universitaires pendant 9 ans.

Les deux prochains grands nombres premiers connus sont ??galement Mersenne Primes: M = _30402457 ^30402457 2 - 1 (43e Mersenne premier connu, 9.152.052 chiffres) et M = _25964951 ^25964951 2 - 1 (42e Mersenne premier connu, 7.816.230 chiffres). Historiquement, le premier plus grand connu a presque toujours ??t?? un premier de Mersenne depuis l'aube des ordinateurs ??lectroniques, car il existe un test de primalit?? particuli??rement rapide pour les num??ros de cette forme, le Test de Lucas-Lehmer pour les nombres de Mersenne.

Le plus grand nombre premier connu qui ne est pas un premier de Mersenne est 19249 ?? 2 ^13018586 + 1 (3.918.990 chiffres), un Nombre de Proth. Ce est aussi le septi??me plus grand nombre premier connu de toute forme. Il a ??t?? constat?? sur 26 mars 2007 par le Dix-sept ou un projet de poitrine et il les rapproche un peu plus pour r??soudre le Probl??me de Sierpinski.

Certains des plus grands nombres premiers pas connu pour avoir une forme particuli??re (ce est pas de formule simple comme celle des nombres premiers de Mersenne) ont ??t?? trouv??s en prenant un morceau de donn??es binaires semi-al??atoires, le convertissant en un nombre n, multipliant par 256 ^k pour un entier positif k, et la recherche de nombres premiers possibles dans l'intervalle [256 ^k n + 1, 256 ^k (n + 1) - 1].

Prix pour trouver des nombres premiers

Le Electronic Frontier Foundation (EFF) a offert un US $ 100 000 prix aux premiers d??couvreurs d'un premier avec au moins 10 millions de chiffres. Ils offrent ??galement 150.000 dollars pour 100 millions de chiffres, et 250.000 $ pour 1 milliard de chiffres. En 2000, ils pay??s $ 50 000 pour 1 millions de chiffres.

Le Factorisation RSA a offert des prix jusqu'?? US $ 200 000 pour trouver les facteurs premiers de certains semiprimes jusqu'?? 2048 bits. Cependant, le d??fi a ??t?? ferm?? en 2007 apr??s beaucoup de petits prix pour les petits semiprimes avaient ??t?? vers??s.

G??n??ralisations du concept Premier

Le concept de nombre premier est si important qu'il a ??t?? g??n??ralis?? de diff??rentes mani??res dans diverses branches des math??matiques.

Premiers ??l??ments dans les anneaux

On peut d??finir ??l??ments premiers et ??l??ments irr??ductibles ?? toute int??gre. Pour toute domaine de factorisation unique, comme l'anneau Z des entiers, l'ensemble des ??l??ments premiers ??gale l'ensemble des ??l??ments irr??ductibles, qui pour Z est {..., -11, -7, -5, -3, -2, 2, 3, 5, 7, 11, ...}.

A titre d'exemple, nous consid??rons le Entiers de Gauss Z [i], ce est-?? nombres complexes de la forme a + bi avec a et b dans Z. Ce est un domaine int??grante, et ses ??l??ments principaux sont la Nombres premiers gaussienne. Notez que la figure 2 est un premier pas gaussienne, car il Facteurs dans le produit des deux nombres premiers de Gauss (1 + i) et (1 - i). L'??l??ment 3, cependant, reste premier dans les entiers de Gauss. En g??n??ral, les nombres premiers rationnels (ie des ??l??ments fondamentaux dans l'anneau Z des entiers) de la forme 4 k + 3 nombres premiers sont gaussiennes, alors que nombres premiers rationnels de la forme 4 k + 1 ne sont pas.

Prime id??aux

En la th??orie des anneaux, une remplace g??n??ralement la notion de nombre avec celui de id??al. Prime id??aux sont un outil et objet d'??tude dans importante alg??bre commutative, th??orie alg??brique des nombres et g??om??trie alg??brique. Les id??aux premiers de l'anneau des entiers sont les id??aux (0), (2), (3), (5), (7), (11), ...

Un probl??me central en th??orie alg??brique des nombres est de savoir comment un id??al premier de facteurs quand il se est lev?? ?? un champ d'extension. Par exemple, dans l'exemple entier gaussien ci-dessus, (2) ramifie en une puissance motrice (1 + i et 1 - i g??n??rer le m??me id??al premier), id??aux premiers de la forme (4 k + 3) sont inertes (rester Premier) , et les id??aux premiers de la forme (4 k + 1) split (sont le produit de deux id??aux premiers distincts).

Primes en th??orie d'??valuation

En la th??orie du champ de classe encore une autre g??n??ralisation est utilis??. Compte tenu d'un arbitraire corps K, on consid??re ??valuations sur K, certaines fonctions de K ?? la R nombres r??els. Chaque telle ??valuation donne un topologie sur K, et deux ??valuations sont appel??s ??quivalents se ils donnent la m??me topologie. Un premier de K (parfois appel?? un lieu de K) est une classe d'??quivalence des valorisations. Avec cette d??finition, les nombres premiers de la zone de Q des nombres rationnels sont repr??sent??s par la norme valeur absolue fonction (connu sous le nom "prime infini") ainsi que par la p valorisations -adiques sur Q, pour tout nombre premier p.

Prime noeuds

Dans la th??orie des n??uds , un n??ud est un Premier noeud qui est, dans un certain sens, ind??composable. Plus pr??cis??ment, il en est une qui ne peut ??tre ??crite comme la noeud somme de deux noeuds non triviaux.

Questions ouvertes

Il ya beaucoup de questions ouvertes sur les nombres premiers. Une tr??s importante est le Hypoth??se de Riemann, qui dit essentiellement que les nombres premiers sont aussi r??guli??rement distribu??s que possible. D'un point de vue physique, il d??clare ?? peu pr??s que l'irr??gularit?? dans la distribution des nombres premiers vient seulement de bruit al??atoire. D'un point de vue math??matique, il d??clare ?? peu pr??s que la distribution asymptotique des nombres premiers (environ 1 / log x des nombres inf??rieurs ?? x sont des nombres premiers, les th??or??me des nombres premiers) vaut aussi pour des intervalles beaucoup plus courtes de longueur sur la racine carr??e de x (pour des intervalles pr??s de x). Cette hypoth??se est g??n??ralement consid??r??es comme correctes, en particulier, l'hypoth??se la plus simple est que les nombres premiers ne devraient pas avoir d'importantes irr??gularit??s sans bonne raison.

Beaucoup de conjectures c??l??bres semblent avoir une tr??s forte probabilit?? d'??tre vrai (dans un sens formel, beaucoup d'entre eux suivent des arguments probabilistes heuristiques simples):

Premier Num??ros Euclide: On ne sait pas si oui ou non il ya un nombre infini de nombres premiers Euclide.

Forte conjecture de Goldbach : Chaque entier pair sup??rieur ?? 2 peut ??tre ??crit comme une somme de deux nombres premiers.

Faible conjecture de Goldbach: Chaque entier impair sup??rieur ?? 5 peut ??tre ??crit comme une somme de trois nombres premiers.

Conjecture des nombres premiers jumeaux: Il ya une infinit?? de nombres premiers jumeaux, des paires de nombres premiers avec la diff??rence 2.

La conjecture de Polignac: Pour tout entier positif n, il existe une infinit?? de nombres premiers cons??cutifs paires de qui diff??rent par 2 n. Lorsque n = 1 ce est la conjecture des nombres premiers jumeaux.

Une forme plus faible de la conjecture de Polignac: Chaque m??me nombre est la diff??rence de deux nombres premiers.

Il est largement admis, il ya une infinit?? de Nombres premiers de Mersenne, mais pas Fermat amorce.

On suppose qu'il ya une infinit?? de nombres premiers de la forme n ² + 1.

Beaucoup de conjectures bien connus sont des cas particuliers de la large Hypoth??se de H. de Schinzel

On suppose qu'il existe une infinit?? de nombres Fibonacci amorce.

Legendre de la conjecture: Il est un nombre premier entre ² et n (n + 1) ² pour tout entier positif n.

De Cramer la conjecture: 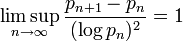$\ Limsup_ {n \ rightarrow \ infty} \ frac {{p_ n + 1} -p_n} {(\ log p_n) ^ 2} = 1$ . Cette conjecture implique Legendre, mais son statut est plus incertain.

Conjecture de Brocard: Il ya toujours au moins quatre premiers entre les carr??s de nombres premiers cons??cutifs sup??rieurs ?? 2.

Tous les quatre Probl??mes de Landau de 1912 sont ??num??r??s ci-dessus et encore non r??solu: Goldbach, nombres premiers jumeaux, Legendre, n ² 1 nombres premiers.

Applications

Pendant longtemps, la th??orie des nombres en g??n??ral, et l'??tude des nombres premiers en particulier, a ??t?? consid??r??e comme l'exemple canonique de math??matiques pures, sans applications en dehors de l'int??r??t d'??tudier le sujet. En particulier, les th??oriciens des nombres tels que la Colombie- math??maticien GH Hardy se vantait de faire un travail qui ne avait absolument aucune importance militaire. Cependant, cette vision a ??t?? bris??e dans les ann??es 1970, quand il a ??t?? annonc?? publiquement que les nombres premiers pourraient ??tre utilis??s comme base pour la cr??ation de algorithmes de cryptographie ?? cl?? publique. Les nombres premiers sont ??galement utilis??s pour Les tables de hachage et des g??n??rateurs de nombres pseudo-al??atoire.

Certains machines ?? rotor ont ??t?? con??us avec un nombre diff??rent de broches sur chaque rotor, le nombre de broches sur l'un ou l'autre premier rotor, ou premier avec le nombre de broches sur tout autre rotor. Cela a permis de g??n??rer le cycle complet des positions de rotor possibles avant de r??p??ter ne importe quelle position.

Cryptographie ?? cl?? publique

Plusieurs algorithmes de cryptographie ?? cl?? publique, comme RSA, sont bas??es sur des grands nombres premiers (par exemple avec 512 bits).

Les nombres premiers dans la nature

Beaucoup de num??ros se produisent dans la nature, et, in??vitablement, certains d'entre eux sont premiers. Il ya, cependant, relativement peu d'exemples de nombres qui apparaissent dans la nature parce qu'ils sont premiers. Par exemple, la plupart ??toiles de mer ont cinq bras, et 5 est un nombre premier. Cependant, il ne existe aucune preuve pour sugg??rer que les ??toiles de mer ont cinq bras parce 5 est un nombre premier. En effet, certaines ??toiles de mer ont des nombres diff??rents de bras. Echinaster luzonicus a normalement six bras, Luidia senegalensis a neuf bras, et Solaster endeca peut avoir jusqu'?? vingt bras. Pourquoi la majorit?? des ??toiles de mer (et la plupart des autres ??chinodermes) ont cinq sym??trie reste un myst??re.

Un exemple de l'utilisation de nombres premiers dans la nature est aussi une strat??gie ??volutionniste utilis??e par cigales du genre Magicicada. Ces insectes passent la plupart de leur vie souterrain larves. Ils ne se transforment en pupes puis sortent de leurs terriers après 13 ou 17 ans, à quel point ils volent, race, puis meurent au bout de quelques semaines tout au plus. La logique de cette méthode semble être que les intervalles de nombres premiers entre émergences, il est très difficile pour les prédateurs d'évoluer qui pourrait se spécialiser en tant que prédateurs sur Magicicadas . Si Magicicadas apparu à un non-premiers intervalles de numéros, dire tous les 12 ans, puis tous les prédateurs apparaissent 2, 3, 4, 6, ou 12 ans serait sûr de les rencontrer. Sur une période de 200 ans, les populations de prédateurs moyenne pendant les flambées hypothétiques de 14 et 15 ans cigales seraient jusqu'à 2% de plus que pendant les épidémies de cigales de 13 et 17 ans. Bien que petit, cet avantage semble avoir été suffisant pour conduire la sélection naturelle en faveur d'un cycle de vie-prime-numérotée pour ces insectes.

Il ya des spéculations que les zéros de la fonction zêta sont reliés aux niveaux de systèmes quantiques complexes d'énergie.

Les nombres premiers dans les arts et la littérature

Les nombres premiers ont influencé de nombreux artistes et écrivains. Le Fran??ais compositeur Olivier Messiaen utilisé nombres premiers à créer de la musique grâce à ametrical "phénomènes naturels". Dans des ??uvres comme La Nativité du Seigneur (1935) et Quatre études de rythme (1949-1950), il emploie simultanément motifs avec des longueurs données par différents nombres premiers pour créer des rythmes imprévisibles: les nombres premiers 41, 43, 47 et 53 apparaissent dans un des études. Selon Messiaen cette façon de composer a été "inspiré par les mouvements de la nature, les mouvements de durées libres et inégaux».

Dans son roman de science fiction contacter, plus tard transformé en unfilm du même nom, laNASAscientifiqueCarl Sagana suggéré que les nombres premiers pourraient être utilisés comme un moyen de communiquer avec des extraterrestres, une idée qu'il avait d'abord mis au point de façon informelle avec l'astronome américainFrank Drake en 1975.

Primé 1993 jeu de Tom Stoppard Arcadia était une tentative consciente de discuter des idées mathématiques sur la scène. Dans la scène d'ouverture, les 13 années vieilles énigmes de l'héroïne sur le dernier théorème de Fermat , impliquant un théorème des nombres premiers.

Beaucoup de films reflètent une fascination populaire avec les mystères de nombres premiers et la cryptographie: des films tels que Le Cube, Sneakers, The Mirror Has Two Faceset A Beautiful Mind, basé sur la biographie du mathématicien et lauréat du prix NobelJohn Forbes Nash parSylvia Nasar.

R??cup??r?? ?? partir de " http://en.wikipedia.org/w/index.php?title=Prime_number&oldid=199034422 "