Infini

Saviez-vous ...

Enfants SOS b??n??voles ont aid?? ?? choisir des articles et ont fait d'autres mat??riels de curriculum m??res SOS chaque regard apr??s une une famille d'enfants parrain??s .

Le symbole de l'infini, ∞, dans plusieurs polices de caract??res.

Infinity (repr??sent?? symboliquement avec ∞) provient des latins infinitas ou ??l'absence de limites." Elle se r??f??re ?? plusieurs concepts distincts (g??n??ralement li??s ?? l'id??e de ??sans fin??) qui se posent dans la philosophie , les math??matiques , et la th??ologie.

En math??matiques , "l'infini" est souvent utilis?? dans des contextes o?? elle est trait??e comme se il se agissait d'un nombre (ie, il compte ou des mesures choses: "un nombre infini de termes") mais ce est un type de "nombre" diff??rente de la nombres r??els . Infinity est li??e ?? des limites , num??ros Aleph, classes dans la th??orie des ensembles , Dedekind-ensembles infinis, grands cardinaux, Le paradoxe de Russell, arithm??tique non-standard, num??ros hyperr??alistes, la g??om??trie projective, nombres r??els ??tendues et la absolue Infini.

Histoire

Les premi??res vues indiennes de l'infini

Le Isha Upanishad de la Yajurveda (c. 4e-3e si??cle avant JC) stipule que "si vous retirez une partie de l'infini ou d'ajouter une partie ?? l'infini, ce qui reste encore est l'infini".

Purnam Adah purnam idam (Ce est plein, ce est plein)

pūrṇāt purnam udacyate (Du plein, le plein est soustrait)

pūrṇasya purnam Adaya (Quand le plein est pris de la pleine)

evāvasiṣyate purnam (La pleine restera encore.) - Isha Upanishad

L'Indien math??matique texte Surya Prajnapti (c. 400 BC) classe tous les num??ros en trois ensembles: ??num??rables, innombrables, et infinis. Chacun de ces a ??t?? subdivis??e en trois ordres:

Enumerable moins, interm??diaire et plus
Innombrables: presque innombrables, vraiment innombrables et innombrablement innombrables
Infini: presque infinie, v??ritablement infini, infiniment infinie

Le Ja??ns ont ??t?? les premiers ?? rejeter l'id??e que tous les infinis ??taient les m??mes ou ??gal. Ils ont reconnu les diff??rents types de infinis: une longueur infinie (une dimension), infinie dans la zone (deux dimensions), infini en volume (trois dimensions), et infini perp??tuellement (nombre infini de dimensions).

Selon Singh (1987), Joseph (2000) et Agrawal (2000), le plus grand nombre d??nombrable N de la ja??ns correspond ?? la notion moderne de aleph-null 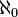$\ Aleph_0$ (Le nombre cardinal de l'ensemble infini de nombres entiers 1, 2, ...), le plus petit cardinal Num??ro transfinite. Le ja??ns ??galement d??fini tout un syst??me de nombres cardinaux infinis, dont le plus grand nombre d??nombrable N est le plus petit.

Dans le travail Jaina sur la th??orie des ensembles , deux types de base de nombres infinis sont distingu??s. Sur la fois physique et motifs ontologiques, une distinction a ??t?? faite entre asaṃkhyāta ("innombrables, innombrables") et Ananta ("sans fin, illimit??"), entre rigidement limit??e et peu infinis born??es.

Logique

Dans la logique d'une infinie argument r??gression est ??une sorte distinctement philosophique de argument tendant ?? d??montrer qu'une th??se est d??fectueux parce qu'il g??n??re une s??rie infinie lorsque soit (forme A) pas cette s??rie existe ou (forme B) ??tait qu'elle existe, la th??se ne aurait pas la r??le (par exemple, de la justification) qu'il est cens?? jouer. "

symbole de l'infini

John Wallis a introduit le symbole de l'infini ?? la litt??rature math??matique.

L'origine pr??cise de la symbole de l'infini "∞" ne est pas claire. Une possibilit?? est sugg??r?? par le nom, il est parfois appel?? la- lemniscate, de la lemniscus latine, signifiant "ruban." On peut imaginer marchant toujours le long d'une simple boucle form??e ?? partir d'un ruban.

Une explication populaire est que le symbole de l'infini est d??riv?? de la forme d'un Ruban de M??bius. Encore une fois, on peut imaginer la marche le long de sa surface pour toujours. Toutefois, cette explication est peu probable, puisque le symbole avait ??t?? utilis?? pour repr??senter l'infini pour plus de deux cents ans avant Ao??t Ferdinand M??bius et Johann Benedict Listing d??couvert la bande de M??bius en 1858 .

Il est ??galement possible qu'il se inspire de plus religieuse / alchimique symbolisme. Par exemple, il a ??t?? trouv?? en tib??tain gravures rupestres, et la ouroboros, ou l'infini serpent, est souvent repr??sent?? sous cette forme.

John Wallis est g??n??ralement cr??dit?? de pr??senter ∞ comme un symbole de l'infini dans 1655 dans les conicis de son De. Une conjecture sur pourquoi il a choisi ce symbole est qu'il a tir?? ?? partir d'un chiffre romain pour 1000 qui a ??t?? ?? son tour d??riv?? du Chiffre ??trusque 1000, qui ressemblait un peu ?? CIƆ et a ??t?? parfois utilis?? pour signifier ??beaucoup??. Une autre conjecture est qu'il a tir?? ?? partir de la lettre grecque ω ( omega), la derni??re lettre de l' alphabet grec .

Une autre possibilit?? est que le symbole a ??t?? choisi parce qu'il ??tait facile de tourner un caract??re "8" par 90 ?? lorsque la composition a ??t?? fait ?? la main. Le symbole est parfois appel?? un ??paresseux huit", ??voquant l'image d'un "8" couch?? sur le c??t??.

Une autre croyance populaire est que le symbole de l'infini est une repr??sentation claire de la sablier tourn?? de 90 ??. De toute ??vidence, cette action entra??nerait la vitre d'heure de prendre un temps infini pour vider pr??sentant ainsi un exemple tangible de l'infini. L'invention du sablier est ant??rieure ?? l'existence du symbole de l'infini permet cette th??orie soit plausible.

Le symbole de l'infini est repr??sent?? dans Unicode par le ∞ de caract??re (U + 221E).

L'infini math??matique

Infinity est utilis?? dans diverses branches des math??matiques.

Calcul

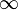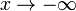En analyse r??elle, le symbole $\ Infty$ , Appel?? "l'infini", d??signe un illimit??e limite . $x \ rightarrow \ infty$ signifie que x cro??t sans borne, et $x \ rightarrow - \ infty$ signifie que la valeur de x diminue sans borne. Si f (t) ≥ 0 pour tout t, puis

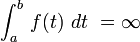$\ Int_ {a} ^ {b} \, f (t) \ dt \ = \ infty$ signifie que f (t) n'a pas forc??ment une zone finie de A ?? B
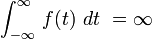$\ Int _ {- \ infty} ^ {\ infty} \, f (t) \ dt \ = \ infty$ signifie que l'aire sous f (t) est infini.
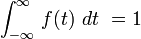$\ Int _ {- \ infty} ^ {\ infty} \, f (t) \ dt \ = 1$ signifie que la zone sous f (t) est ??gal ?? 1

Infinity est ??galement utilis?? pour d??crire s??rie infinie:

$\ sum_ {i = 0} ^ {\ infty} \, f (i) = x$ signifie que la somme de la s??rie infinie converge vers une certaine valeur r??elle x.
$\ Sum_ {i = 0} ^ {\ infty} \, f (i) = \ infty$ signifie que la somme de la s??rie infinie diverge dans le sens sp??cifique que les sommes partielles se d??velopper sans borne.

Propri??t??s alg??briques

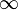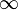Infinity est souvent utilis?? non seulement pour d??finir une limite mais comme une valeur dans le syst??me des nombres r??els affinement ??tendue. Points marqu??s $\ Infty$ et $- \ Infty$ peuvent ??tre ajout??s ?? la espace topologique des nombres r??els, produisant les deux points compactification des nombres r??els. Ajout de propri??t??s alg??briques pour cela nous donne les nombres r??els prolong??es. Nous pouvons ??galement traiter $\ Infty$ et $- \ Infty$ comme le m??me, ce qui conduit ?? un point le compactifi?? des nombres r??els, qui est le droite projective r??elle. La g??om??trie projective introduit ??galement une droite ?? l'infini en g??om??trie plane , et ainsi de suite pour les dimensions sup??rieures.

La ligne de nombre r??el ??tendu ajoute deux ??l??ments appel??s infini ( 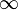$\ Infty$ ), Plus grand que tous les autres nombres r??els prolong??es, et l'infini n??gatif ( $- \ Infty$ ), ?? moins que tous les autres nombres r??els ??tendues, pour lesquelles des op??rations arithm??tiques peuvent ??tre ex??cut??es.

Analyse complexe

Comme dans l'analyse r??elle, dans analyse complexe du symbole 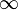$\ Infty$ , Appel?? "l'infini", d??signe un illimit??e limite . $x \ rightarrow \ infty$ signifie que l'ampleur $| X |$ x cro??t au-del?? d'une valeur assign??e. Un Point marqu?? 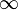$\ Infty$ peuvent ??tre ajout??s au plan complexe en tant que espace topologique donnant la un point compactifi?? du plan complexe. Lorsque cela est fait, l'espace qui en r??sulte est une unidimensionnelle vari??t?? complexe, ou surface de Riemann , appel?? le plan complexe prolong??e ou Sph??re de Riemann. Les op??rations arithm??tiques similaires ?? celles donn??es ci-dessous pour les nombres r??els prolong??es peuvent ??galement ??tre d??finis, se il n'y a pas de distinction dans les signes (donc une exception est que l'infini ne peut pas ??tre ajout?? ?? lui-m??me). D'autre part, ce genre de d??bordement permet division par z??ro, ?? savoir 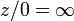$z / 0 = \ infty$ pour tout nombre complexe z. Dans ce contexte est souvent utile de consid??rer fonctions m??romorphes que des cartes dans la sph??re de Riemann prenant la valeur de 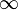$\ Infty$ aux p??les. Le domaine d'une fonction de valeur complexe peut ??tre ??tendue pour inclure le point ?? l'infini ainsi. Un exemple important de ces fonctions est le groupe des Transformations de M??bius.

Analyse non standard

La formulation initiale du calcul par Newton et Leibniz utilis?? des quantit??s infinit??simales. Au XXe si??cle, il a ??t?? montr?? que ce traitement pourrait ??tre mis sur un pied rigoureuse ?? travers diverses syst??mes logiques, y compris analyse infinit??simale lisse et analyse non standard. Dans ce dernier, sont infinit??simales inversible, et leurs inverses sont des nombres infinis. Les infinis dans ce sens font partie d'un tout domaine; il n'y a pas d'??quivalence entre eux comme avec l'cantorienne transfinites. Par exemple, si H est un nombre infini, alors H + H = 2H et H + 1 sont diff??rents nombres infinis.

La th??orie des ensembles

Un type de "l'infini" diff??rent sont les ordinaux et cardinaux infinis de la th??orie des ensembles. Georg Cantor a d??velopp?? un syst??me de nombres transfinis, dans lequel le premier cardinal transfini est aleph-null 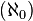$(\ Aleph_0)$ , Le cardinalit?? de l'ensemble des nombres naturels . Cette conception math??matique moderne de l'infini quantitatif d??velopp?? ?? la fin du XIXe si??cle du travail par Cantor, Gottlob Frege, Richard Dedekind et d'autres, en utilisant l'id??e de collections, ou ensembles.

L'approche de Dedekind ??tait essentiellement d'adopter l'id??e de -un ?? un la correspondance comme une norme pour comparer la taille des ensembles, et ?? rejeter le point de vue de Galileo (qui d??coule de Euclid ) que l'ensemble ne peut pas ??tre la m??me taille que la partie. Un ensemble infini peut simplement ??tre d??finie comme ayant une m??me taille que la au moins une de ses " propres "parties; cette notion de l'infini est appel?? Dedekind infinie.

Cantor a d??fini deux types de nombres infinis, les nombres ordinaux et la nombres cardinaux. Les nombres ordinaux peuvent ??tre identifi??s avec ensembles bien ordonn??s, ou comptage effectu?? ?? ne importe quel point d'arr??t, y compris les points apr??s un nombre infini ont d??j?? ??t?? comptabilis??s. G??n??raliser fini et l'infini ordinaire s??quences qui sont des cartes positifs entiers conduit ?? mappages de nombres ordinaux, et des s??quences transfinis. Les nombres cardinaux d??finissent la taille des ensembles, ce qui signifie combien de membres qu'ils contiennent, et peuvent ??tre normalis??es en choisissant le premier num??ro d'ordre d'une certaine taille pour repr??senter le nombre cardinal de cette taille. La plus petite de l'infini ordinal est celle des nombres entiers positifs, et tout ensemble qui a la cardinalit?? des nombres entiers est infini d??nombrable. Si un ensemble est trop grand pour ??tre mis en correspondance un ?? un avec les nombres entiers positifs, il est appel?? innombrables. Les vues de Cantor pr??valu et les math??matiques modernes accepte infini actuel. Certains prolong??es nombre de syst??mes, tels que la num??ros hyperr??els, int??grent les nombres ordinaires (finis) et un nombre infini de diff??rentes tailles.

Notre intuition acquise dans ensembles finis d??compose lorsqu'il se agit de ensembles infinis. Un exemple de ceci est H??tel de Hilbert.

Cardinalit?? du continuum

Un des r??sultats les plus importants de Cantor ??tait que le cardinalit?? du continuum ( 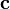$\ Mathbf c$ ) Est sup??rieure ?? celle des nombres naturels ( ${\ Aleph_0}$ ); ce est, il ya de plus r??el que des chiffres des nombres R naturel N. A savoir, Cantor a montr?? que $\ Mathbf {c} = 2 ^ {\ aleph_0}> {\ aleph_0}$ (Voir Argument de la diagonale de Cantor).

Le hypoth??se de continuum d??clare qu'il n'y a pas de nombre cardinal entre le cardinal des r??els et la cardinalit?? des nombres naturels, ce est- 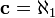$\ Mathbf {c} = \ aleph_1$ . Toutefois, cette hypoth??se ne peut ??tre ni prouv??e ni r??fut??e dans le largement accept??e Th??orie des ensembles de Zermelo-Fraenkel, m??me en supposant que le Axiom of Choice.

Cardinal arithm??tique peut ??tre utilis?? pour montrer non seulement que le nombre de points dans un v??ritable ligne de nombre est ??gal au nombre de points dans ne importe quel tron??on de cette ligne, mais que ce ne est ??gal au nombre de points sur un plan et, en fait, dans ne importe quel espace de dimension finie. Ces r??sultats sont tr??s contre-intuitif, car ils impliquent qu'il existe des sous-ensembles appropri??s d'un ensemble infini S qui ont la m??me taille que S.

Le premier de ces r??sultats est apparent en consid??rant, par exemple, la tangente fonction, qui fournit un une-??-une correspondance entre le intervalle [-0.5π, 0.5π] et R (voir aussi H??tel de Hilbert). Le deuxi??me r??sultat a ??t?? prouv?? par Cantor en 1878, mais ne est devenue apparente intuitivement en 1890, lorsque Giuseppe Peano a pr??sent?? le courbes de remplissage d'espace, lignes courbes que tordre et tourner assez pour remplir l'ensemble de ne importe quel carr?? ou cube, ou hypercube, ou un espace de dimension finie. Ces courbes peuvent ??tre utilis??s pour d??finir un un-??-un entre les points dans le c??t?? d'un carr?? et ceux du carr??.

Il est ??galement possible de montrer que les ensembles de cardinal strictement sup??rieur 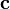$\ Mathbf c$ exister. Ils comprennent, par exemple:

l'ensemble de tous les sous-ensembles de R, ?? savoir le ensemble de R de puissance, P ??crite (R) ou 2 ^R
l'ensemble R ^R de toutes les fonctions de R ?? R

Tous les deux ont cardinalit?? $2 ^ \ mathbf {c} = \ beth_2$ (Voir Beth).

Math??matiques sans d??bordement

Leopold Kronecker a rejet?? la notion de l'infini et a commenc?? une ??cole de pens??e, dans le philosophie des math??matiques appel?? finitisme qui a influenc?? l'??cole philosophique et math??matique de constructivisme math??matique.

L'infini physique

Dans la physique , des approximations de nombres r??els sont utilis??s pour mesures continues et nombres naturels sont utilis??s pour mesures discr??tes (ce est ?? dire de comptage). On suppose donc que par les physiciens pas quantit?? mesurable pourrait avoir une valeur infinie, par exemple en prenant une valeur infinie dans un prolong??e syst??me des nombres r??els (voir aussi: Num??ro hyperr??el), ou en exigeant le comptage d'un nombre infini d'??v??nements. Il est par exemple impossible pour un pr??sum?? corps d'avoir la masse infinie ou d'??nergie infinie. Il existe le concept d'entit??s infinite (comme un infini onde plane), mais il n'y a aucun moyen de produire de telles choses.

Il convient de souligner que cette pratique de refuser des valeurs infinies pour des quantit??s mesurables ne est pas venu de a priori ou motivations id??ologiques, mais plut??t de motivations plus m??thodologiques et pragmatiques. L'un des besoins de toute th??orie physique et scientifique est de donner des formules utilisables qui correspondent ?? la r??alit?? ou du moins approximative. Par exemple si un objet de masse gravitationnelle infinie existait, toute utilisation de la formule pour calculer la force gravitationnelle conduirait ?? un r??sultat infini, ce qui serait d'aucune utilit?? puisque le r??sultat serait toujours le m??me quelle que soit la position et la masse de l'autre objet. La formule serait utile ni pour calculer la force entre deux objets de masse finie, ni pour calculer leurs mouvements. Si un objet de masse infinie existait, ne importe quel objet de masse finie serait attir?? avec force infinie (et donc l'acc??l??ration) par l'objet masse infinie, qui ne est pas ce que nous pouvons observer dans la r??alit??.

Ce point de vue ne signifie pas que l'infini ne peut pas ??tre utilis?? en physique. Pour sak??, des calculs, des ??quations, des th??ories et des approximations de commodit?? utilisent souvent s??rie infinie, non born??s fonctions , etc., et peut impliquer quantit??s infinies. Les physiciens mais exigent que le r??sultat final soit physiquement significative. Dans la th??orie quantique des champs infinis surgir, qui doivent ??tre interpr??t??es de mani??re ?? aboutir ?? un r??sultat physiquement significatif, un processus appel?? renormalisation . Une application o?? infinis se posent est la quantification des temp??ratures thermodynamiques .

Cependant, il ya certaines circonstances actuellement accept??s lorsque le r??sultat final est infini. Un exemple en est les trous noirs . Les physiciens ont v??rifi?? que, quand une ??toile exp??riences effondrement gravitationnel, elle finira par se r??duire ?? un point de taille z??ro, et donc avoir une densit?? infinie. Ceci est un exemple de ce qu'on appelle un singularit?? math??matique ou un point o?? les lois des math??matiques, de la physique et, par cons??quent, se d??composent. Certains physiciens pensent maintenant la singularit?? peut ??tre physiquement r??el, et ont depuis tourn?? leur attention vers la recherche de nouvelles math??matiques o?? infinis possibles.

Infinity en cosmologie

Une question int??ressante est de savoir si l'infini actuel existe dans notre physique univers il ya une infinit?? de nombreuses stars:? Est-ce que l'univers ont volume infini? Est-ce que l'espace "durer ??ternellement"? Ce est une question ouverte importante de la cosmologie . Notez que la question de l'??tre infini est logiquement distincte de la question d'avoir des limites. La surface ?? deux dimensions de la Terre, par exemple, est finie, mais n'a pas de bord. En marche / voile / tout droit assez longtemps, vous revenez ?? l'endroit exact que vous avez commenc?? ?? partir. L'univers, au moins en principe, pourrait avoir un effet semblable topologie ; si vous pilotez votre vaisseau spatial tout droit assez longtemps, peut-??tre vous auriez ??ventuellement revoir votre point de d??part. Si, cependant, l'univers est toujours en expansion , alors vous ne pourrait jamais revenir ?? votre point de d??part, m??me ?? une ??chelle de temps infini.

repr??sentations informatiques de l'infini

Le La norme IEEE ?? virgule flottante sp??cifie les valeurs de d??bordement positifs et n??gatifs; ceux-ci peuvent ??tre le r??sultat de d??passement arithm??tique, division par z??ro, ou d'autres op??rations exceptionnelles.

Certains langages de programmation (par exemple, J et UNITY) sp??cifier plus et les moins des ??l??ments, ce est- comparer des valeurs (respectivement) sup??rieur ou inf??rieur ?? toutes les autres valeurs. Ceux-ci peuvent ??galement ??tre d??sign??s haut et en bas, ou plus l'infini et moins l'infini; ils sont utiles comme valeurs de sentinelles dans algorithmes impliquant tri, recherche ou fen??trage. Dans les langues qui ne ont pas les ??l??ments les plus grands et les moins, mais ne permettent surcharge op??rateurs relationnels, il est possible de cr??er des ??l??ments plus grands et les moins (avec une certaine frais g??n??raux, et le risque d'incompatibilit?? entre les impl??mentations).

Perspective et points ?? l'infini dans les arts

Perspective ??uvre utilise le concept de l'imaginaire points de fuite, ou points ?? l'infini, situ??s ?? une distance infinie de l'observateur. Cela permet aux artistes de cr??er des peintures qui 'r??aliste' repr??sentent la distance et le raccourcissement des objets. Artiste MC Escher est sp??cialement connu pour employer le concept de l'infini dans son travail dans cette affaire et d'autres moyens.

R??cup??r?? ?? partir de " http://en.wikipedia.org/w/index.php?title=Infinity&oldid=198896642 "