La th??orie des ensembles

La th??orie des ensembles est la branche de math??matiques qui ??tudie ensembles, qui sont des collections d'objets. Bien que tout type d'objets peut ??tre recueilli dans un ensemble, la th??orie des ensembles est appliqu??e le plus souvent ?? des objets qui sont pertinents pour les math??matiques.

L'??tude moderne de la th??orie des ensembles a ??t?? initi?? par Cantor et Dedekind dans les ann??es 1870. Apr??s la d??couverte de paradoxes dans la th??orie des ensembles informelle, de nombreux syst??mes d'axiomes ont ??t?? propos??es au d??but du XXe si??cle, dont la Zermelo-Fraenkel axiomes, avec le axiome du choix, sont le plus connu.

La th??orie des ensembles, formalis?? en utilisant la logique du premier ordre , est le syst??me de base le plus commun pour les math??matiques. Le langage de la th??orie des ensembles est utilis?? dans les d??finitions de presque tous les objets math??matiques, comme les fonctions et les concepts de la th??orie des ensembles sont int??gr??s tout au long du programme de math??matiques. Faits ??l??mentaires sur les jeux et appartenance ?? un ensemble peuvent ??tre introduits ?? l'??cole primaire, avec des diagrammes de Venn , pour ??tudier des collections d'objets physiques banales. Op??rations ??l??mentaires comme le jeu union et intersection peuvent ??tre ??tudi??s dans ce contexte. Des concepts plus avanc??s tels que cardinalit?? sont une partie standard du programme de math??matiques de premier cycle.

Au-del?? de son utilisation comme un syst??me fondamental, la th??orie des ensembles est une branche de math??matiques dans son propre droit, avec une communaut?? de recherche active. La recherche contemporaine en th??orie des ensembles comprend une collection vari??e de sujets, allant de la structure du nombre r??el en ligne ?? l'??tude de la coh??rence des grands cardinaux.

Histoire

Voir Johnson (1972) pour un traitement de livre-longueur. Sujets math??matiques ??mergent et ??voluent g??n??ralement par des interactions entre de nombreux chercheurs. Le point d'origine de la th??orie des ensembles est quelque peu inhabituel en ce qu'il peut ??tre identifi?? en tant que document 1874 par Georg Cantor : ??Sur une propri??t?? caract??ristique de tous les nombres r??els alg??briques".

En commen??ant par le travail de Zeno autour de 450 avant JC, les math??maticiens avait ??t?? strugglinging avec le concept de l'infini . Particuli??rement remarquable est le travail de Bernard Bolzano dans la premi??re moiti?? du 19??me si??cle. La compr??hension moderne de l'infini a commenc?? 1867 ?? 1871, avec Georg Cantor travail de l 'sur la th??orie des nombres. Une r??union entre 1872 et Cantor Dedekind beaucoup influenc?? la pens??e de Cantor et a abouti ?? Cantor (1874).

Le travail de Cantor initialement polaris?? les math??maticiens de son temps. Tandis que Weierstrass et Dedekind soutenu Cantor, Kronecker, maintenant consid??r?? comme un des fondateurs de constructivisme math??matique, n'a pas fait. Mais l'utilit?? des concepts tels que cantoriennes correspondance un-??-un entre les ensembles, sa preuve qu'il ya plus nombres r??els que des nombres entiers, et le ??infinit?? de infinis" ("paradis Cantor??), le op??ration de jeu de puissance donne lieu ??, a finalement conduit ?? l'acceptation g??n??ralis??e de la th??orie des ensembles cantorienne.

La prochaine vague d'excitation dans la th??orie des ensembles est venu autour de 1900, quand il a ??t?? d??couvert que la th??orie des ensembles cantorienne a donn?? lieu ?? plusieurs contradictions, appel??s ou antinomies paradoxes. Russell et Zermelo trouv?? ind??pendamment le paradoxe le plus simple et le plus connu, maintenant appel?? Le paradoxe de Russell et impliquant ??l'ensemble de tous les ensembles qui ne sont pas membres d'eux-m??mes." Il est clair que cet ensemble ne peut pas ??tre membre d'elle-m??me, et donc il doit ??tre membre d'elle-m??me! En 1899, Cantor avait lui-m??me pos?? la question: "quel est le nombre cardinal ? de l'ensemble de tous les ensembles " et a obtenu un paradoxe li??. Il a r??alis?? plus tard que ces paradoxes ne sont pas simplement mis th??orique, et que, dans la logique de la phrase "cette phrase est fausse" donne lieu ?? un probl??me similaire, car si la phrase est vraie, elle doit ??tre fausse. Kurt G??del utilis?? ce fait dans le 1931 la preuve de son c??l??bre th??or??me de l'incompl??tude.

L'??lan de la th??orie des ensembles ??tait telle que le d??bat sur les paradoxes n'a pas conduit ?? son abandon. Le travail de Zermelo en 1908 et Fraenkel en 1922 a abouti ?? la canonique th??orie des ensembles axiomatique ZFC, qui est exempt de paradoxes. Le travail de tels que les analystes Lebesgue a d??montr?? la grande utilit?? math??matique de la th??orie des ensembles. th??orie des ensembles axiomatique est devenue tiss?? dans le tissu m??me des math??matiques comme nous le connaissons aujourd'hui.

Concepts de base

La relation fondamentale entre les objets et ensembles est le adh??sion ou "elementhood?? relation; donn?? un joint d'objet et un ensemble A, soit O est un membre de A ou il ne est pas un membre. La relation fondamentale entre deux ensembles est le sous-ensemble relation, aussi appel?? ensemble inclusion. Par exemple, {a, b} est un sous-ensemble {a, b, c}, mais {a, d} ne est pas.

Tout comme il existe des op??rations arithm??tiques qui op??rent sur les chiffres, il ya des op??rations dans la th??orie des ensembles qui fonctionnent sur des ensembles. Par exemple, en commen??ant par les ensembles {1, 2, 3} et {2, 3, 4}, la op??ration d'union produit un nouvel ensemble {1, 2, 3, 4} contenant tous les ??l??ments qui sont dans les deux ensemble, et l' intersection op??ration produit l'ensemble {2, 3} constitu?? de tous les ??l??ments qui sont ?? la fois dans des d??cors originaux. Des op??rations suppl??mentaires sur les ensembles comprennent:

• Compl??mentation: l'ensemble des ??l??ments d'un ensemble U qui ne sont pas dans un ensemble A est appel?? le compl??ment de A par rapport ?? U, not??e . Cette terminologie est utilis??e le plus souvent lorsque U est un ensemble implict ??universel??, comme dans l'??tude des diagrammes de Venn . L'ensemble des ??l??ments de U pas dans A est aussi appel?? la diff??rence de jeu, not??e .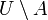
• Le la diff??rence sym??trique des deux ensembles est constitu?? de tous les ??l??ments qui sont exactement l'un des deux ensembles.
• Le Produit cart??sien de deux ensembles A et B se compose de tous les couples (a, b) o?? a est un membre de A et B est un membre de B.
• Le powerset d'un ensemble A se compose de tous les sous-ensembles de A. Par exemple, le powerset de {1, 2} est {{}, {1}, {2}, {1,2}}.

Interpr??tations

Une id??e cl?? dans la th??orie des ensembles est le von Neumann univers de ensembles purs. Un ensemble est pur si tous ses membres sont des ensembles, tous les membres de ses membres sont des ensembles, et ainsi de suite. Par exemple, l'ensemble ne contenant que l'ensemble vide est un ensemble non vide pur. Il est commun dans la th??orie des ensembles pour restreindre l'attention sur les jeux purs, plut??t que d'??tudier des ensembles arbitraires, et de nombreux syst??mes axiomatiques de la th??orie des ensembles sont uniquement destin??es ?? axiomatiser les ensembles purs.

Les ensembles purs sont dispos??s dans la hi??rarchie cumulatif bas?? sur combien de leurs membres, les membres des membres, etc. sont imbriqu??s. Chaque ensemble est attribu?? un nombre ordinal α dans cette hi??rarchie, connu comme son rang. Inversement, pour chaque ordinal α l'ensemble V _α est d??fini pour contenir tous les jeux qui sont affect??s de rang plus sup??rieur ?? α. L'attribution de grades se fait par r??currence transfinie: si la borne sup??rieure sur les rangs des ??l??ments d'un ensemble X est α rang α alors X est affect?? + 1.

La th??orie des ensembles axiomatique

Les concepts de base de la th??orie des ensembles peuvent ??tre ??tudi??es de mani??re informelle et intuitive plut??t que axiomatique. Ainsi la th??orie des ensembles tr??s ??l??mentaire peut ??tre enseign?? dans les ??coles primaires en utilisant, par exemple, les diagrammes de Venn . Cette approche intuitive donne lieu ?? antinomies, le plus simple et le plus connu dont ??tre Paradoxe. Russell la th??orie des ensembles axiomatique a ??t?? initialement con??u pour bannir ces antinomies.

Les syst??mes les plus ??tudi??s de la th??orie des ensembles sont bas??s sur le concept d'un hi??rarchie cumulative de jeux. Ces syst??mes sont disponibles en deux saveurs, ceux dont ontologie se compose de:

• D??finit seul. Cela comprend la th??orie la plus commune axiomatique des ensembles, Th??orie des ensembles de Zermelo-Fraenkel (ZFC), qui comprend le axiome du choix. Des fragments de ZFC comprennent:
  • Zermelo la th??orie des ensembles, qui remplace le Sch??ma d'axiomes de remplacement avec celui de s??paration;
  • La th??orie des ensembles g??n??ral, un petit fragment de La th??orie des ensembles Zermelo suffisante pour le Axiomes de Peano et ensembles finis;
  • Kripke-Platek th??orie des ensembles, qui omet les axiomes de l'infini, powerset, et choix, et affaiblit les sch??mes de axiome de s??paration et remplacement.
• Les classes appropri??es ainsi que des ensembles. Ceci comprend Von Neumann-Bernays-G??del th??orie des ensembles, qui a la m??me force que ZFC pour th??or??mes sur les seuls ensembles, et Th??orie des ensembles de Morse-Kelley, qui est plus fort que ZFC.

Les syst??mes NFU (avec urelements) et NF (qui en sont d??pourvues) ne sont pas fond??es sur une hi??rarchie cumulative. NF et NFU comprennent un ??ensemble de tous les ensembles", par rapport ?? laquelle chaque ensemble a un compl??ment. D'autre part, NF (mais pas NFU) permet ?? des syst??mes d'ensembles pour lesquels la axiome du choix ne tient pas.

Syst??mes de la th??orie des ensembles constructive, comme CST, CZF et IZF, int??grer leurs axiomes fix??s dans logique intuitionniste lieu de logique du premier ordre . Pourtant, d'autres syst??mes acceptent la norme logique du premier ordre , mais disposent d'une relation d'appartenance non standard. Il se agit notamment la th??orie des ensembles rugueux et th??orie des ensembles flous, dans lequel la valeur d'un formule atomique incarnant la relation d'appartenance ne est pas simplement Vrai et Faux. Le mod??les de valeur bool??enne de ZFC sont un sujet connexe.

Applications

Presque tous les concepts math??matiques sont maintenant d??finis formellement en termes d'ensembles et des concepts th??oriques fix??s. Par exemple, les structures math??matiques aussi divers que graphiques, collecteurs , anneaux, et espaces vectoriels sont tous d??finis comme des ensembles ayant diverses propri??t??s (axiomatiques). ??quivalence et relations d'ordre sont omnipr??sents dans les math??matiques, la th??orie de relations est enti??rement fond??es sur la th??orie des ensembles.

La th??orie des ensembles est aussi un syst??me fondamental prometteuse pour beaucoup des math??matiques. Depuis la publication du premier volume de Principia Mathematica, il a ??t?? affirm?? que la plupart voire tous les th??or??mes math??matiques ou peuvent ??tre obtenues en utilisant un ensemble d'axiomes bien con??ues pour la th??orie des ensembles, augment??e de nombreuses d??finitions, en utilisant en premier ou deuxi??me logique de commande. Par exemple, les propri??t??s des naturels et nombres r??els peuvent ??tre d??riv??es au sein th??orie des ensembles, que chaque syst??me de notation peut ??tre identifi?? avec un ensemble de classes d'??quivalence sous une appropri??e relation d'??quivalence dont le champ est un peu ensemble infini.

La th??orie des ensembles comme fondement de l'analyse math??matique , topologie , l'alg??bre abstraite , et math??matiques discr??tes est ??galement ?? controverse; math??maticiens acceptent que (en principe) th??or??mes dans ces domaines peuvent ??tre obtenues ?? partir des d??finitions pertinentes et les axiomes de la th??orie des ensembles. Quelques d??rivations compl??tes de th??or??mes math??matiques complexes ?? partir de la th??orie des ensembles ont ??t?? formellement v??rifi??e, cependant, parce que ces d??rivations formelles sont souvent beaucoup plus longtemps que la langue naturelle preuves math??maticiens souvent pr??sente. Un projet de v??rification, Metamath, comprend d??rivations de plus de 10 000 th??or??mes ?? partir de la Axiomes ZFC et utilisant logique du premier ordre .

Les domaines d'??tudes

La th??orie des ensembles est un domaine majeur de la recherche en math??matiques, avec de nombreux sous-domaines interd??pendants.

La th??orie des ensembles combinatoire

La th??orie des ensembles combinatoire concerne les extensions de finis combinatoire d'ensembles infinis. Cela comprend l'??tude des arithm??tique cardinale et l'??tude des extensions de Le th??or??me de Ramsey tel que le Th??or??me de Erdos-Rado.

La th??orie des ensembles descriptive

La th??orie des ensembles descriptive est l'??tude des sous-ensembles de la ligne r??elle et, plus g??n??ralement, des sous-ensembles de Espaces polonais. Il commence par l'??tude des pointclasses dans le Borel hi??rarchie et se ??tend ?? l'??tude des hi??rarchies plus complexes telles que la et la hi??rarchie projective Hi??rarchie Wadge. Beaucoup de propri??t??s des ensembles Borel peuvent ??tre ??tablis dans ZFC, mais prouver ces propri??t??s d??tiennent pour des ensembles plus complexes n??cessite axiomes suppl??mentaires li??s ?? d??terminisme et grands cardinaux.

Le domaine de la la th??orie des ensembles descriptive efficace est entre th??orie des ensembles et th??orie r??cursivit??. Il comprend l'??tude des pointclasses maigre, et est ??troitement li??e ?? hyperarithmetical th??orie. Dans de nombreux cas, les r??sultats de la th??orie descriptive des ensembles classiques ont des versions efficaces; dans certains cas, de nouveaux r??sultats sont obtenus en prouvant la version en vigueur premi??re et se ??tendant ensuite ("relativiser") pour le rendre plus largement applicable.

Une zone r??cente des pr??occupations de recherche Borel ??quivalence et relations plus complexes d??finissables relations d'??quivalence . Cela a d'importantes applications ?? l'??tude des invariants dans de nombreux domaines des math??matiques.

Th??orie des ensembles flous

En th??orie des ensembles comme Cantor d??fini et Zermelo et Fraenkel axiomatis??, un objet est soit un membre d'un ensemble ou non. En th??orie des ensembles flous cette condition a ??t?? assouplie par Zadeh si un objet a un degr?? d'appartenance ?? un ensemble, comme nombre compris entre 0 et 1. Par exemple, le degr?? d'appartenance d'une personne dans l'ensemble des "personnes de grande taille" est plus souple que d'un simple oui ou non r??ponse et peut ??tre un nombre r??el tels que 0,75.

Th??orie du mod??le interne

Un mod??le interne de Th??orie des ensembles de Zermelo-Fraenkel (ZF) est un transitive cat??gorie qui comprend tous les ordinaux et satisfait tous les axiomes de ZF. L'exemple type est la constructible univers L d??velopp?? par G??del. L'??tude des mod??les internes des extensions de ZF est d'int??r??t dans la th??orie des ensembles, car il peut ??tre utilis?? pour prouver des r??sultats de coh??rence. Par exemple, on peut montrer que quel que soit un mod??le de ZF V satisfait la hypoth??se du continu ou le axiome du choix, le mod??le interne L construit ?? l'int??rieur du mod??le original satisfaire ?? la fois l'hypoth??se de continuum et l'axiome du choix. Ainsi l'hypoth??se que ZF est conforme (a ne importe quel mod??le que ce soit) implique que ZF avec ces deux principes est conforme.

L'??tude de mod??les internes est commune dans l'??tude de d??terminisme et de grands cardinaux, surtout lorsque l'on consid??re axiomes tels que l'axiome de d??terminisme qui contredisent l'axiome du choix. M??me si un mod??le fixe de la th??orie des ensembles satisfait l'axiome du choix, il est possible pour un mod??le interne ?? l'??chec pour satisfaire l'axiome du choix. Par exemple, l'existence de suffisamment grands cardinaux implique qu'il ya un mod??le interne satisfaisant l'axiome de d??terminisme (et donc pas satisfaire l'axiome du choix).

Grands cardinaux

Un grand cardinal est un nombre cardinal avec une propri??t?? suppl??mentaire. Beaucoup de ces propri??t??s sont ??tudi??es, y compris cardinaux inaccessibles, cardinaux mesurables, et beaucoup plus. Ces propri??t??s impliquent g??n??ralement le nombre cardinal doit ??tre tr??s grande, avec l'existence d'un cardinal avec la propri??t?? improuvable dans Zermelo-Fraenkel indiqu?? la th??orie des ensembles.

D??terminisme

D??terminisme se r??f??re au fait que, sous des hypoth??ses appropri??es, certains jeux ?? deux joueurs d'information parfaite sont d??termin??s d??s le d??part dans le sens o?? un joueur doit avoir une strat??gie gagnante. L'existence de ces strat??gies a des cons??quences importantes dans la th??orie descriptive des ensembles, que l'hypoth??se selon laquelle une cat??gorie plus large de jeux est d??termin??e souvent implique qu'une cat??gorie plus large de jeux aura une propri??t?? topologique. Le axiome de d??terminisme (AD) est un objet d'??tude important; bien incompatible avec l'axiome du choix, AD implique que tous les sous-ensembles de la ligne r??elle sont bien ??lev??s (en particulier, mesurables et avec la propri??t?? ensemble parfait). AD peut ??tre utilis?? pour prouver que le Degr??s Wadge ont une structure ??l??gante.

Forcer

Paul Cohen a invent?? for??ant tout en recherchant un mod??le de ZFC dans lequel le hypoth??se de continuum ??choue. Forcer est contigu ?? un mod??le donn?? de th??orie des ensembles ensembles suppl??mentaires afin de cr??er un mod??le plus grand avec des propri??t??s d??termin??es par la construction et le mod??le original. Par exemple, la construction de Cohen jouxte sous-ensembles suppl??mentaires des nombres naturels sans changer les nombres cardinaux du mod??le original. Forcer est aussi l'un des deux modes de preuve coh??rence relative par des m??thodes finitiste, l'autre m??thode ??tant mod??les de valeur bool??enne.

Invariants Cardinal

Un invariant cardinal est une propri??t?? de la ligne r??elle mesur??e par un nombre cardinal. Par exemple, un invariant bien ??tudi??e est la plus petite cardinalit?? d'une collection de ensembles maigres r??els dont l'union est toute la ligne r??elle. Ce sont des invariants dans le sens que les deux mod??les isomorphes de la th??orie des ensembles doivent donner le m??me cardinal pour chaque invariant. De nombreux invariants cardinaux ont ??t?? ??tudi??s, et les relations entre eux sont souvent complexes et li??es ?? axiomes de la th??orie des ensembles.

Topologie ensembliste

Set-??tudes th??oriques de topologie questions de topologie g??n??rale qui sont mis en th??orie dans la nature ou qui n??cessitent des m??thodes de la th??orie des ensembles avanc?? pour leur solution. Beaucoup de ces th??or??mes sont ind??pendants de ZFC, n??cessitant axiomes forts pour leur preuve. Un probl??me c??l??bre est le question de l'espace Moore normale, une question en topologie g??n??rale qui a fait l'objet d'intenses recherches. La r??ponse ?? la question d'espace Moore normale a ??t?? finalement av??r?? ??tre ind??pendant de ZFC.

Objections ?? la th??orie des ensembles

Depuis sa cr??ation, il ya eu quelques math??maticiens qui ont oppos?? ?? l'utilisation de la th??orie des ensembles comme une fondation pour les math??matiques, pr??tendant que ce est juste un jeu qui comprend des ??l??ments de fantaisie. Errett ??v??que a rejet?? la th??orie des ensembles comme ?? Dieu math??matiques de l ', que nous devrions laisser ?? Dieu de faire. " Aussi Ludwig Wittgenstein interrog?? en particulier le traitement des infinis, qui concerne ??galement ZF. Les points de vue de Wittgenstein sur les fondements des math??matiques ont ??t?? critiqu??es par Paul Bernays, et ??troitement ??tudi??e par Crispin Wright, entre autres.

L'objection la plus fr??quente ?? la th??orie des ensembles est le vue constructiviste que les math??matiques sont vaguement li??es au calcul et que la th??orie des ensembles na??ve est formalis??e avec l'ajout d'??l??ments noncomputational.

Topos th??orie a ??t?? propos??e comme une alternative ?? la th??orie des ensembles axiomatique traditionnelle. la th??orie de Topos peut ??tre utilis?? pour interpr??ter diverses solutions de rechange ?? la th??orie des ensembles tels que constructivisme, th??orie des ensembles finis, et la th??orie des ensembles calculable.