
Diagramme de Venn
Renseignements g??n??raux
Enfants SOS ont produit une s??lection d'articles de wikipedia pour les ??coles depuis 2005. Les m??res SOS chaque regard apr??s une une famille d'enfants parrain??s .
Diagrammes de Venn sont illustrations utilis??es dans la branche des math??matiques connues comme la th??orie des ensembles . Invent?? en 1881 par John Venn, ils montrent tous les possibles math??matiques ou logiques relations entre ensembles (groupes de choses). Ils se composent normalement de chevauchement des cercles . Par exemple, dans un jeu de deux diagramme de Venn, un cercle peut repr??senter tout ce qui est liquide ?? temp??rature ambiante, tandis qu'un autre cercle peut repr??senter l'ensemble de tous les ??l??ments chimiques. La zone de chevauchement (intersection) repr??senterait alors des choses qui sont ?? la fois liquide ?? temp??rature et ??l??ments ambiante, par exemple le mercure. D'autres formes peuvent ??tre utilis??s (voir ci-dessous), ce qui est n??cessaire pour plus de trois ensembles.
Origines

Le Hull-n?? Colombie philosophe et math??maticien John Venn (1834-1923) a pr??sent?? le diagramme de Venn en 1881 .
Un vitrail dans Caius College, Cambridge , o?? Venn a ??tudi?? et a pass?? la plupart de sa vie, lui comm??more et repr??sente un diagramme de Venn.
Exemples

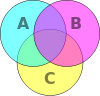
Le cercle orange ( ensemble A) peut repr??senter, par exemple, toutes les cr??atures vivantes qui sont ?? deux pattes. Le cercle bleu, (ensemble B) peut repr??senter des ??tres vivants qui peuvent voler. La zone o?? les cercles bleus et orange chevauchent contient toutes les cr??atures vivantes qui peuvent voler et qui ont deux jambes - par exemple, des perroquets. (Imaginez chaque type de cr??ature comme un point quelque part dans le sch??ma s??par??e.)
Les humains et les pingouins seraient dans le cercle orange, dans la partie qui ne chevauche pas avec le cercle bleu. Les moustiques ont six pattes, et voler, de sorte que le point de d??part pour les moustiques seraient dans la partie du cercle bleu qui ne chevauche pas avec l'orange. Les choses qui ne sont pas deux jambes et ne peut pas voler (par exemple, les baleines et les araign??es) seraient tous repr??sent??s par des points en dehors de deux cercles. Techniquement, le diagramme de Venn ci-dessus peut ??tre interpr??t?? comme "les relations de s??ries A et B qui peuvent avoir certains ??l??ments (mais pas tous) en commun".
La surface combin??e des ensembles A et B est appel?? le union de A et B, d??sign??e par l'AUB. Le syndicat, dans ce cas contient toutes les choses qui ont soit deux jambes, ou qui volent, ou les deux.
La zone ?? la fois A et B, o?? les deux ensembles se chevauchent, est appel?? le intersection de A et B, not??e A ∩ B. L'intersection des deux ensembles ne est pas vide, parce que les cercles se chevauchent, ce est ?? dire il ya des cr??atures qui sont ?? la fois dans l'orange et cercles bleus.
Parfois, un rectangle appel?? " Ensemble universel "est dessin?? autour du diagramme de Venn pour montrer l'espace de toutes les choses possibles. Comme mentionn?? ci-dessus, une baleine serait repr??sent?? par un point qui ne est pas dans l'union, mais il est dans l'Univers (des ??tres vivants, ou de tous les choses, selon la fa??on dont on a choisi de d??finir l'univers pour un sch??ma particulier).
Extensions ?? un plus grand nombre d'ensembles
 | 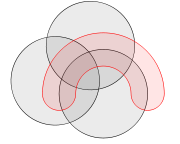 |  | 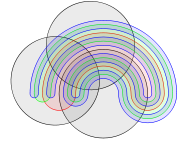 |
Diagrammes de Venn ont g??n??ralement trois sets. Venn a tenu ?? trouver des chiffres sym??triques ... ??l??gante ?? se repr??senter un plus grand nombre de jeux et il a con??u un sch??ma de jeu ?? l'aide de quatre ellipses . Il a ??galement donn?? une construction de diagrammes de Venn avec un nombre quelconque de courbes, o?? chaque courbe successive est entrelac?? avec des courbes pr??c??dentes, ?? commencer par le sch??ma 3-cercle.
Sym??triques simples diagrammes de Venn
Henderson DW montr?? en 1963 que l'existence d'un sch??ma de -Venn n avec n -fois sym??trie de rotation implique que n est premier . Il a ??galement montr?? que ces diagrammes de Venn sym??triques existent lorsque n est 5 ou 7. En 2002 Peter Hamburger trouv?? diagrammes de Venn sym??triques pour n = 11 et en 2003, Griggs, Killian et Savage ont montr?? que les diagrammes de Venn sym??triques existent pour tous les autres nombres premiers. Ainsi diagrammes de Venn sym??triques existent si et seulement si n est un nombre premier.
Diagrammes de Venn de Edwards
 |  |
 |  |
AWF Edwards a donn?? une construction d'un plus grand nombre de jeux qui met en vedette certaines sym??tries. Sa construction est r??alis?? en projetant le diagramme de Venn sur une sph??re . Trois ensembles peuvent ??tre facilement repr??sent??s en prenant trois h??misph??res ?? angle droit (x ≥0, y et z ≥0 ≥0). Un quatri??me ensemble peut ??tre repr??sent?? en prenant une courbe similaire ?? la couture sur une balle de tennis qui serpente de haut en bas autour de l'??quateur. Les ensembles obtenues peuvent ensuite ??tre projet??es en arri??re au plan pour donner diagrammes ?? cr??maill??re avec des nombres de dents croissante. Ces diagrammes ont ??t?? con??us lors de la conception d'un vitrail fen??tre in memoriam de Venn.
Autres diagrammes
Diagrammes de Venn d'Edwards sont topologiquement ??quivalents aux sch??mas con??u par Branko Gr??nbaum qui ont ??t?? bas?? autour d'intersection des polygones avec des nombres de c??t??s croissante. Ils sont aussi des repr??sentations en 2 dimensions de hypercubes.
Smith a con??u des sch??mas semblables en utilisant n -Set sinuso??des avec des ??quations y = sin (x) 2 i / 2 i, 0≤i≤ n -2.
Charles Lutwidge Dodgson (aka Lewis Carroll) a con??u un ensemble de cinq diagramme.
l'utilisation en salle de classe
Diagrammes de Venn sont souvent utilis??s par les enseignants dans la salle de classe comme un m??canisme pour aider les ??l??ves ?? comparer et contraster deux articles. Caract??ristiques sont ??num??r??es dans chaque section du diagramme, avec les caract??ristiques communes ??num??r??es dans la section de chevauchement.
