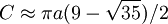Ellipse
Renseignements g??n??raux
Arrangeant une s??lection Wikipedia pour les ??coles dans le monde en d??veloppement sans internet ??tait une initiative de SOS Enfants. SOS Children travaille dans 45 pays africains; pouvez-vous aider un enfant en Afrique ?


En math??matiques , une ellipse (du grec ἔλλειψις, litt??ralement absence) est un lieu des points dans un plan de telle sorte que la somme des distances ?? deux points fixes est une constante. Les deux points fixes sont appel??s foyers (pluriel de concentrer). Une autre d??finition serait une ellipse qui est le chemin trac?? par un point dont la distance d'un point fixe, appel??e la mise au point, maintient un rapport constant avec moins d'un son ?? distance ?? partir d'une ligne droite ne passant pas par le foyer, appel?? le directrice.
Vue d'ensemble
Une ellipse est un type de section conique : si un surface conique est coup?? avec un plan qui ne coupe pas la base du c??ne, l'intersection du c??ne et plan est une ellipse. Pour une preuve ??l??mentaire ?? court de cela, voir Th??or??me de Dandelin.
Alg??briquement , une ellipse est une courbe dans le plan cart??sien d??fini par une ??quation de la forme
tel que 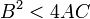 , O?? tous les coefficients sont r??els, et lorsque plus d'une solution, d??finissant une paire de points (x, y) sur l'ellipse, existe.
, O?? tous les coefficients sont r??els, et lorsque plus d'une solution, d??finissant une paire de points (x, y) sur l'ellipse, existe.
Une ellipse peut ??tre ??tabli avec deux broches, une boucle de ficelle, et un crayon. Les broches sont plac??es aux foyers et les broches et un crayon sont enferm??s ?? l'int??rieur de la cha??ne. Le crayon est plac?? sur le papier ?? l'int??rieur de la cha??ne, de sorte que la cha??ne est tendue. La cha??ne va former un triangle . Si le crayon est d??plac?? de sorte que la cha??ne reste tendue, la somme des distances du crayon pour les broches restera constante, r??pondant ?? la d??finition d'une ellipse.
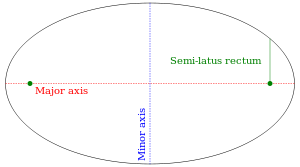
Le segment de droite AB, qui passe par les foyers et se termine sur l'ellipse, est appel?? l'axe principal. Le grand axe est le plus long segment qui peut ??tre obtenu en joignant deux points de l'ellipse. Le CD du segment de ligne, qui passe par le centre (?? mi-chemin entre les foyers), perpendiculaire ?? l'axe principal, et se termine sur l'ellipse, est appel?? l'axe secondaire. Le demi-grand axe (d??sign?? par A dans la figure) est une moiti?? de l'axe majeur: le segment de ligne du centre, ?? travers une mise au point, et sur le bord de l'ellipse. De m??me, la demi-petit axe (d??sign?? par b sur la figure) est une moiti?? de l'axe mineur.
Si les deux foyers co??ncident, alors l'ellipse est un cercle ; en d'autres termes, un cercle est un cas particulier d'une ellipse, une o?? le excentricit?? est nulle.
Une ellipse centr??e ?? la origine peut ??tre consid??r??e comme l'image du cercle unit?? dans une application lin??aire associ??e ?? une matrice sym??trique  ,
, 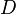 ??tre un matrice diagonale avec les valeurs propres de
??tre un matrice diagonale avec les valeurs propres de  , Qui sont tous deux r??el positif, le long de la diagonale principale, et
, Qui sont tous deux r??el positif, le long de la diagonale principale, et 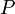 ??tre un vrai matrice unitaire comportant les colonnes comme vecteurs propres de
??tre un vrai matrice unitaire comportant les colonnes comme vecteurs propres de  . Ensuite, les axes de l'ellipse se trouveront le long des vecteurs propres de
. Ensuite, les axes de l'ellipse se trouveront le long des vecteurs propres de  Et le (racine carr??e des valeurs propres) sont les longueurs des demi-grands axes et demi-petit.
Et le (racine carr??e des valeurs propres) sont les longueurs des demi-grands axes et demi-petit.
Une ellipse peut ??tre produit en multipliant les coordonn??es x de tous les points sur un cercle par une constante, sans modifier les coordonn??es y. Ceci est ??quivalent ?? l'??tirage du cercle dans la direction x.
Excentricit??
La forme d'une ellipse peut ??tre exprim??e par un nombre appel?? la l'excentricit?? de l'ellipse, classiquement d??sign??  . L'excentricit?? est un nombre non n??gatif inf??rieur ?? 1 et sup??rieur ou ??gal ?? 0. Ce est la valeur constante du rapport de la distance d'un point sur l'ellipse ?? partir d'une mise au point pour que de la directrice correspondante. Une excentricit?? de 0 implique que les deux foyers occupent le m??me point et que l'ellipse est un cercle .
. L'excentricit?? est un nombre non n??gatif inf??rieur ?? 1 et sup??rieur ou ??gal ?? 0. Ce est la valeur constante du rapport de la distance d'un point sur l'ellipse ?? partir d'une mise au point pour que de la directrice correspondante. Une excentricit?? de 0 implique que les deux foyers occupent le m??me point et que l'ellipse est un cercle .
Pour une ellipse dont le demi-grand axe a et demi-petit axe b, l'excentricit?? est
Plus l'excentricit?? est importante, plus le rapport de a ?? b, et donc plus l'ellipse allong??e.
Si c est ??gal ?? la distance entre le centre de chaque point, puis
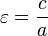 .
.
La distance c est connue comme l'excentricit?? de l'ellipse lin??aire. La distance entre les foyers est 2 c ou 2 aε.
Aussi,
o?? 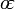 est le excentricit?? angulaire.
est le excentricit?? angulaire.
??quations
Une ellipse avec une demi-grand axe a et demi-petit axe b, centr??e au point 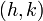 et ayant son axe principal parall??le ?? l'axe des x peut ??tre sp??cifi?? par l'??quation
et ayant son axe principal parall??le ?? l'axe des x peut ??tre sp??cifi?? par l'??quation
 .
.
Cette ellipse peut ??tre exprim??e param??trique que
o?? 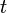 peut ??tre limit?? ?? l'intervalle
peut ??tre limit?? ?? l'intervalle 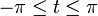 .
.
Forme param??trique d'une ellipse en rotation par un angle 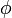 :
:
La formule pour les directrixes est
 .
.
Si  = 0 et
= 0 et 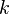 = 0 (ce est ?? dire, si le centre est ?? l'origine (0,0)), alors nous pouvons exprimer cette ellipse en coordonn??es polaires par l'??quation
= 0 (ce est ?? dire, si le centre est ?? l'origine (0,0)), alors nous pouvons exprimer cette ellipse en coordonn??es polaires par l'??quation
o??  est l'excentricit?? de l'ellipse.
est l'excentricit?? de l'ellipse.
Avec une mise au point ?? l'origine, ??quation polaire de l'ellipse est
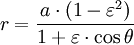 .
.
Un Forme de Gauss-mapp??:
a la normale 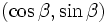 .
.
Rectum semi-latus et coordonn??es polaires
Le rectum de semi-latus d'une ellipse, g??n??ralement d??sign?? 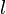 ( L minuscule), est la distance entre un foyer de l'ellipse de l'ellipse elle-m??me, mesur??e le long d'une ligne perpendiculaire ?? l'axe principal. Elle est li??e ??
( L minuscule), est la distance entre un foyer de l'ellipse de l'ellipse elle-m??me, mesur??e le long d'une ligne perpendiculaire ?? l'axe principal. Elle est li??e ?? 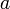 et
et  (Demi-axes de l'ellipse) par la formule
(Demi-axes de l'ellipse) par la formule 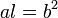 ou, si vous utilisez l'excentricit??,
ou, si vous utilisez l'excentricit??, 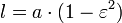 .
.
En coordonn??es polaires , une ellipse avec une mise au point ?? l'origine et l'autre sur l'axe des x n??gatif est donn??e par l'??quation
Une ellipse peut ??galement ??tre consid??r?? comme une projection d'un cercle: un cercle sur un plan ?? l'angle φ ?? l'horizontale de la projection verticale sur un plan horizontal donne une ellipse d'excentricit?? p??ch?? φ, ?? condition φ ne est pas 90 ??.
Espace et la circonf??rence
Le zone d??limit??e par une ellipse est πab, o?? (comme avant) a et b sont demi-grands axes et demi-petit de l'ellipse.
Le circonf??rence 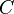 d'une ellipse est
d'une ellipse est  O?? la fonction
O?? la fonction 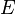 est la compl??te de l'int??grale elliptique deuxi??me type.
est la compl??te de l'int??grale elliptique deuxi??me type.
L'exact s??rie infinie est:
Ou:
Un bien approximation est Ramanujan:
qui peut aussi se ??crire:
Pour le cas particulier o?? le petit axe est la moiti?? du grand axe, on obtient:
ou 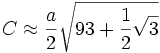 (Meilleure approximation).
(Meilleure approximation).
Plus g??n??ralement, le longueur de l'arc d'une partie de la circonf??rence, en fonction de l'angle sous-tendu, est donn??e par une incomplet int??grale elliptique. La fonction inverse , l'angle sous-tendu en fonction de la longueur d'arc, est donn??e par la fonctions elliptiques.
Stretching et projection
Une ellipse peut ??tre uniform??ment ??tir?? le long d'un axe quelconque, dans ou en dehors du plan de l'ellipse, et il sera toujours une ellipse. L'ellipse ??tir??e aura des propri??t??s diff??rentes (peut-??tre chang?? excentricit?? et semi-longueur d'axe principal, par exemple), mais il sera toujours une ellipse (ou une ellipse d??g??n??r??: un cercle ou une ligne). De m??me, toute projection oblique sur un r??sultat d'avion dans une section conique. Si la projection est une courbe ferm??e dans le plan, la courbe est une ellipse ou une ellipse d??g??n??r??e.
propri??t?? de r??flexion
Supposons un elliptique miroir avec une source de lumi??re ?? l'un des foyers. Puis tous les rayons sont r??fl??chi ?? un seul point - le second foyer. Comme aucun autre courbe a une telle propri??t??, il peut ??tre utilis?? comme une autre d??finition d'une ellipse. Dans un cercle, toute la lumi??re serait r??fl??chie vers le centre depuis toutes les tangentes sont orthogonal au rayon.
Les ondes sonores sont refl??t??es d'une mani??re similaire, donc dans une grande salle elliptique une personne debout ?? un foyer peut entendre une personne debout ?? un autre accent remarquablement bien. Une telle pi??ce est appel??e une chambre de murmure. Des exemples sont le Collection nationale de Hall Statuaire au US Capitol (o?? John Quincy Adams est dit avoir utilis?? cette propri??t?? pour ??coute sur les questions politiques), lors d'une exposition sur le son ?? la Mus??e des sciences et de l'industrie de Chicago , en face de la Universit?? de l'Illinois ?? Urbana-Champaign Foellinger Auditorium, et aussi ?? une chambre de c??t?? du Palais de Charles V, dans le Alhambra.
Ellipses en physique
Dans le 17??me si??cle , Johannes Kepler a expliqu?? que le orbites long de laquelle les plan??tes se d??placent autour du Soleil sont des ellipses dans sa premi??re loi du mouvement plan??taire . Plus tard, Isaac Newton a expliqu?? cela comme un corollaire de son la loi de la gravitation universelle.
Plus g??n??ralement, dans le gravitationnelle probl??me ?? deux corps, si les deux corps sont li??s les uns aux autres (ce est ?? dire, l'??nergie totale est n??gative), leurs orbites sont ellipses semblables avec la common barycentre ??tant l'un des foyers de chaque ellipse. L'autre objectif de soit ellipse a pas connu signification physique. Fait int??ressant, l'orbite de ces deux organes dans le cadre de l'autre de r??f??rence est ??galement une ellipse, avec l'autre corps ?? une mise au point.
La solution g??n??rale pour un Oscillateur harmonique ?? deux ou plus dimensions est ??galement une ellipse, mais cette fois avec l'origine de la force situ?? au centre de l'ellipse.
En optique, un indice d??crit l'ellipso??de indice de r??fraction d'un mat??riau en fonction de la direction ?? travers ce mat??riau. Cela se applique uniquement aux mat??riaux qui sont optiquement anisotrope. Voir aussi bir??fringence.
Ellipses en infographie
Dessin d'une ellipse comme un primitive graphique est commun dans des banques de pr??sentation standard, telles que le Macintosh API QuickDraw, Windows Device Interface GDI (Graphics) et le Windows Presentation Foundation (WPF). Souvent, ces biblioth??ques sont limit??es et ne peuvent dessiner une ellipse avec soit l'axe principal ou ?? l'horizontale de l'axe secondaire. Jack Bresenham chez IBM est le plus c??l??bre pour l'invention des primitives de dessin 2D, y compris ligne et le dessin de cercle, en utilisant des op??rations enti??res seulement rapides telles que l'addition et la branche sur bit de retenue. Une g??n??ralisation efficace pour dessiner des ellipses a ??t?? invent?? en 1984 par Jerry Van Aken (IEEE CG & A, septembre 1984).
Ce qui suit est un exemple de code JavaScript en utilisant la formule param??trique pour une ellipse pour calculer un ensemble de points. L'ellipse peut ??tre approch??e puis en reliant les points par des lignes.
/ ** * Cette fonction retourne un tableau contenant 36 points pour dessiner une ellipse *. * *param X {} deux coordonn??e X *param y {} deux coordonn??e Y *param un {} Demi-grand axe ?? double *param b} {deux demi-petit axe * angle deparam {} ?? double angle de l'ellipse */ function calculateEllipse ( x , y , a , b , angle , steps ) { if ( steps == null ) steps = 36 ; var points = [ ] ; var beta = - angle / 180 * Math . PI ; var sinbeta = Math . sin ( beta ) ; var cosbeta = Math . cos ( beta ) ; for ( var i = 0 ; i < 360 ; i += 360 / steps ) { var alpha = i / 180 * Math . PI ; var sinalpha = Math . sin ( alpha ) ; var cosalpha = Math . cos ( alpha ) ; var X = x + ( a * cosalpha * cosbeta - b * sinalpha * sinbeta ) ; var Y = y + ( a * cosalpha * sinbeta + b * sinalpha * cosbeta ) ; points. push ( new OpenLayers. Geometry . Point ( X , Y ) ) ; } return points ; }
Une cons??quence avantageuse de l'utilisation de la formule param??trique ne est que la densit?? des points est plus grand l?? o?? il est le plus courbure. Ainsi, le changement de pente entre chaque point successif est faible, ce qui r??duit la "effet dents de scie" apparent de l'approximation.

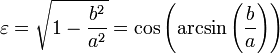






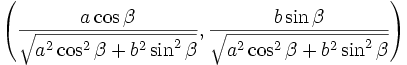

![C = 2 \ pi un \ left [{1 - \ gauche ({1 \ over 2} \ right) ^ 2 \ varepsilon ^ 2 - \ gauche ({1 \ cdot 3 \ plus de 2 \ cdot 4} \ right) ^ 2 {\ varepsilon ^ 4 \ plus de 3} - \ gauche ({1 \ cdot 3 \ cdot 5 \ plus de 2 \ cdot 4 \ cdot 6} \ right) ^ 2 {\ varepsilon ^ 6 \ over5} - \ dots} \ right] \! \,](../../images/93/9311.png)
![C = 2 \ pi un \ sum_ {n = 0} ^ \ infty {\ left \ lbrace - \ left [\ prod_ {m = 1} ^ n \ gauche ({2m-1 \ 2m} \ right) \ right ] ^ 2 {\ varepsilon ^ {2n} \ over 2n - 1} \ right \} rbrace](../../images/93/9312.png)
![C \ approx \ pi \ left [3 (a + b) - \ sqrt {(3a + b) (a + 3b)} \ right]! \ \,](../../images/93/9313.png)
![C \ approx \ pi un \ left [3 (1+ \ sqrt {1- \ varepsilon ^ 2}) - \ sqrt {(3+ \ sqrt {1- \ varepsilon ^ 2}) (1 + 3 \ sqrt {1 -! \ varepsilon ^ 2})} \ right] \ \,](../../images/93/9314.png)