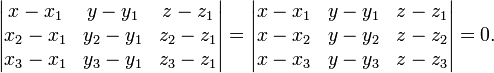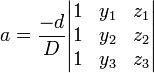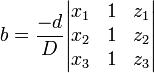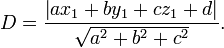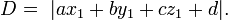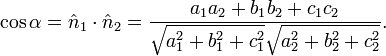Avion (g??om??trie)

Renseignements g??n??raux

SOS Enfants produite ce site pour les ??coles ainsi que ce site de vid??o sur l'Afrique . SOS Enfants a regard?? des enfants en Afrique depuis quarante ans. Pouvez-vous aider dans leur travail en Afrique ?

Deux plans se coupant dans l'espace ?? trois dimensions

En math??matiques , un avion est un bidimensionnelle collecteur ou surface qui est parfaitement plat. Officieusement, il peut ??tre consid??r?? comme une feuille infiniment vaste et infiniment mince orient??e dans certains espace. Formellement, ce est un espace affine de dimension deux.

Lorsque l'on travaille dans l'espace euclidien ?? deux dimensions, l'article d??fini est utilis??, l'avion, de se r??f??rer ?? tout l'espace. De nombreuses t??ches fondamentales dans la g??om??trie , la trigonom??trie et graphique sont effectu??es dans l'espace ?? deux dimensions, ou en d'autres termes, dans le plan. Beaucoup des math??matiques peut ??tre et a ??t?? r??alis??e dans le plan, notamment dans les domaines de la g??om??trie , la trigonom??trie , th??orie des graphes et graphique.

La g??om??trie euclidienne

Dans l'espace euclidien un avion est un surface de telle sorte que, compte tenu de toute deux distincte points de la surface, la surface contient ??galement les uniques ligne droite qui passe par ces points.

La structure fondamentale de ces deux plans sera toujours le m??me. En math??matiques ce est d??crit comme l'??quivalence topologique . Officieusement cependant, cela signifie que les deux plans se ressemblent.

Un avion peut ??tre d??termin??e uniquement par l'une des suivantes (ensembles de) objets:

trois points non align??s (ce est ?? dire, ne se trouvant sur la m??me ligne )
une ligne et un point non sur la ligne
deux lignes avec un point d'intersection
deux lignes parall??les

Avions int??gr??s dans R ³

Cette section concerne sp??cifiquement les avions embarqu??s en trois dimensions: pr??cis??ment, dans ℝ ^3.

Propri??t??s

Dans l'espace euclidien ?? trois dimensions, nous pouvons exploiter les faits suivants qui ne d??tiennent pas de dimensions sup??rieures:

Deux avions sont soit parall??les, soit ils se croisent en ligne.
Une ligne est soit parall??le ?? un plan ou croise en un point unique ou est contenue dans le plan.
Deux lignes perpendiculaires ?? un m??me plan doivent ??tre parall??les les uns aux autres.
Deux plans perpendiculaires ?? la m??me ligne doivent ??tre parall??les les uns aux autres.

D??finir un plan avec un point et un vecteur normal

Dans un espace ?? trois dimensions, un autre moyen important de d??finir un plan est en sp??cifiant un point et une vecteur normal au plan.

Laisser 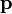$\ P gras$ ??tre le point que nous souhaitons trouver dans le plan, et laisser 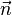$\ Vec n$ un vecteur normal au plan diff??rent de z??ro. Le plan souhait?? est l'ensemble de tous les points 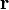$\ R gras$ tel que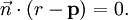 $\ Vec n \ cdot (r- p gras \) = 0.$

Si nous ??crivons 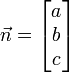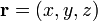$\ Vec n = \ begin {} bmatrix un \\ b \\ c \ end {} bmatrix$ , $\ R gras = (x, y, z)$ et d comme le produit scalaire 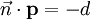$\ Vec n \ cdot \ p gras = -d$ , Puis l'avion 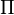$\ Pi$ est d??termin??e par la condition 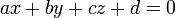$ax + by + cz + d = 0 \,$ , O?? a, b, c et d sont des nombres r??els et a, b et c ne sont pas tous nuls.

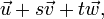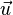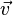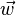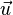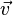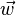Alternativement, un plan peut ??tre d??crit param??trique que l'ensemble des points de la forme $\ Vec {u} + s \ vec {v} + t \ vec {w},$ o?? s et t plage sur tous les nombres r??els, et $\ Vec {u}$ , $\ Vec {v}$ et $\ Vec {w}$ sont donn??s vecteurs d??finissant le plan. $\ Vec {u}$ des points de l'origine ?? un point arbitraire sur le plan, et $\ Vec {v}$ et $\ Vec {w}$ peut ??tre visualis?? comme ?? partir de 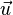$\ Vec {u}$ et pointant dans des directions diff??rentes le long du plan. 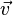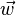$\ Vec {v}$ et $\ Vec {w}$ peut, mais ne ont pas ?? ??tre perpendiculaire (mais ils ne peuvent pas ??tre align??s).

D??finir un plan passant par trois points

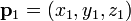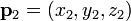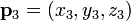Le plan passant par trois points $\ P_1 gras = (x 1, y_1, z_1)$ , $\ P_2 gras = (x_2, Y_2, Z_2)$ et $\ P_3 gras = (x_3, y_3, z_3)$ peut ??tre d??fini comme l'ensemble des points (x, y, z) qui correspondent aux caract??ristiques suivantes d??terminants ??quations:

$\ Begin {} vmatrix x - x 1 et y - y_1 & z - z_1 \\ x_2 - x_1 & Y_2 - y_1 & Z_2 - z_1 \\ x_3 - x_1 & y_3 - y_1 & z_3 - z_1 \ end {} vmatrix = \ begin { vmatrix} x - x 1 et y - y_1 & z - z_1 \\ x - y x_2 & - Y_2 & z - Z_2 \\ x - y x_3 & - y_3 & z - z_3 \ end {} vmatrix = 0.$

Pour d??crire le plan comme une ??quation sous la forme 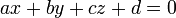$ax + by + cz + d = 0$ , R??soudre le syst??me d'??quations suivant:

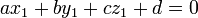
$\, Ax_1 + by_1 + cz_1 + d = 0$

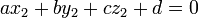
$\, Ax_2 + by_2 + cz_2 + d = 0$

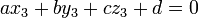$\, Ax_3 + by_3 + cz_3 + d = 0$ .

Ce syst??me peut ??tre r??solu en utilisant Cramer r??gle et les manipulations de la matrice de base. Laisser 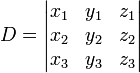$D = \ begin {} vmatrix x_1 & y_1 & z_1 \\ x_2 & Y_2 & Z_2 \\ x_3 & y_3 & z_3 \ end {} vmatrix$ . Ensuite,

$a = \ frac {} -d {D} \ begin {} vmatrix 1 & y_1 & z_1 \\ 1 & Y_2 & Z_2 \\ 1 & y_3 & z_3 \ end {} vmatrix$

$b = \ frac {} -d {D} \ begin {} vmatrix x_1 & 1 & z_1 \\ x_2 & 1 & Z_2 \\ x_3 & 1 & z_3 \ end {} vmatrix$

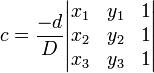$c = \ frac {} -d {D} \ begin {} vmatrix x_1 & y_1 & 1 \\ x_2 & Y_2 & 1 \\ x_3 & y_3 & 1 \ end {} vmatrix$ .

Ces ??quations sont param??trique d. R??glage d ??gal ?? ne importe quel nombre non nulle et son remplacement dans ces ??quations donnera un ensemble de solution.

Cet avion peut ??galement ??tre d??crit par le "point et un vecteur normal" prescription ci-dessus.

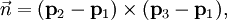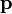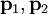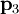Un vecteur appropri?? normale est donn??e par la produit vectoriel $\ Vec n = (\ p_2 gras - p_1 \ gras) \ times (\ P_3 gras - p_1 \ gras),$ et le point $\ P gras$ peut ??tre consid??r?? comme ??tant l'un des points donn??s $\ P_1 gras, \ p_2 gras$ ou $\ P_3 gras$ .

Distance d'un point ?? un plan

Pour un avion 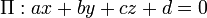$\ Pi: ax + by + cz + d = 0 \,$ et un point 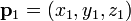$\ P_1 gras = (x 1, y_1, z_1)$ pas n??cessairement se trouvant dans l'avion, la distance la plus courte ?? partir de 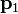$\ P_1 gras$ par rapport au plan est

$D = \ frac {\ left | a + b x_1 y_1 + c + d z_1 \ right |} {\ sqrt {a ^ 2 + b ^ 2 + c ^ 2}}.$

Il se ensuit que 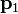$\ P_1 gras$ situ??e dans le plan si et seulement si D = 0.

Si 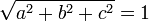$\ Sqrt {a ^ 2 + b ^ 2 + c ^ 2} = 1$ ce qui signifie que a, b et c sont normalis??es alors l'??quation devient

$D = \ | a + b x_1 y_1 + c + d z_1 |.$

Ligne d'intersection entre deux plans

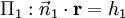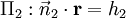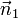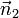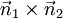Compte tenu des plans d'intersection d??crites par $\ Pi_1: \ vec n_1 \ cdot \ r = gras h_1$ et $\ Pi_2: \ vec n_2 \ cdot \ r = gras H_2$ , La ligne d'intersection perpendiculaire ?? la fois $\ N_1 vec$ et $\ N_2 vec$ et donc parall??le ?? $\ Vec n_1 \ times \ vec n_2$ .

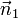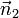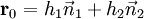Si nous supposons en outre que $\ N_1 vec$ et $\ N_2 vec$ sont orthonorm??e puis le point le plus proche sur la ligne d'intersection ?? l'origine est $\ Gras r_0 = h_1 \ n_1 vec + H_2 \ n_2 vec$ .

Di??dre

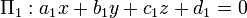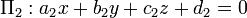Compte tenu des deux plans d'intersection d??crites par $\ Pi_1: a_1 x + y + b_1 c_1 z + d_1 = 0 \,$ et $\ Pi_2: a_2 x + y + b_2 c_2 z + d_2 = 0 \,$ , Le angle di??dre entre eux est d??fini comme ??tant l'angle $\ Alpha$ entre leurs directions normales:

$\ Cos \ alpha = \ hat n_1 \ cdot \ hat n_2 = \ frac {a_1 a_2 + b_1 b_2 + c_1 c_2} {\ sqrt {a_1 ^ 2 + b_1 ^ 2 + c_1 ^ 2} \ sqrt {a_2 ^ 2 + b_2 ^ 2 + c_2 ^ 2}}.$

Planes dans divers domaines des math??matiques

En plus de son familier g??om??trique la structure, avec isomorphismes qui sont isom??tries par rapport au produit int??rieur habitude, le plan peut ??tre consult?? ?? divers autres niveaux de abstraction. Chaque niveau d'abstraction correspond ?? un particulier cat??gorie.

?? un extr??me, tout g??om??trique et concepts m??triques peuvent ??tre tomb?? ?? quitter le topologique avion, qui peut ??tre consid??r?? comme un id??alis??e homotopiquement feuille de caoutchouc trivial infinie, qui conserve une notion de proximit??, mais n'a pas de distances. Le plan topologique a un concept d'une trajectoire lin??aire, mais pas de concept d'une ligne droite. Le plan topologique, ou son ??quivalent le disque ouvert, est le voisinage topologique de base utilis?? pour construire surfaces (ou 2-vari??t??s) class??s dans topologie de basse dimension. Isomorphismes du plan topologique sont tous continu bijections. Le plan topologique est le cadre naturel pour la branche la th??orie des graphes qui traite graphes planaires, et les r??sultats comme le Th??or??me des quatre couleurs .

L'avion peut ??galement ??tre consid??r??e comme une espace affine, dont les isomorphismes sont des combinaisons de traductions et des cartes lin??aires non singuli??res. De ce point de vue il n'y a pas de distances, mais colin??arit?? et des rapports de distance sur ne importe quelle ligne sont pr??serv??s.

G??om??trie diff??rentielle consid??re un plan comme un v??ritable deux dimensions collecteur , un plan topologique qui est pourvu d'un la structure diff??rentielle. Encore une fois, dans ce cas, il n'y a pas de notion de la distance, mais il est maintenant un concept de finesse de cartes, par exemple un diff??rentiables ou chemin lisse (selon le type de structure diff??rentielle appliqu??e). Les isomorphismes dans ce cas sont bijections avec le degr?? de diff??rentiabilit?? choisi.

Dans la direction oppos??e de l'abstraction, nous pouvons appliquer une structure de champ compatible avec le plan g??om??trique, donnant lieu ?? la plan complexe et la r??gion majeure de analyse complexe. Le domaine complexe n'a que deux isomorphismes qui quittent la ligne r??elle fix??, l'identit?? et conjugaison.

De la m??me mani??re que dans le cas r??el, le plan peut ??galement ??tre consid??r??e comme la plus simple, une dimension (sur les nombres complexes) vari??t?? complexe, parfois appel?? la ligne complexe. Toutefois, ce point de vue contraste avec le cas de l'avion comme une v??ritable collecteur deux dimensions. Les isomorphismes sont tous bijections conforme du plan complexe, mais les seules possibilit??s sont les cartes qui correspondent ?? la composition d'une multiplication par un nombre complexe et d'une traduction.

En outre, la g??om??trie euclidienne (qui a z??ro courbure partout) ne est pas la seule g??om??trie que l'avion peut avoir. Le plan peut ??tre donn?? une g??om??trie sph??rique en utilisant le projection st??r??ographique. Cela peut ??tre consid??r?? comme pla??ant une sph??re sur le plan (comme une balle sur le sol), en supprimant le point le plus haut, et en projetant la sph??re sur le plan de ce point). Ce est l'une des saillies qui peuvent ??tre utilis??s dans la fabrication d'une carte ?? plat d'une partie de la surface de la Terre. La g??om??trie r??sultante a une courbure constante positive.

En variante, le plan peut ??galement ??tre donn?? une m??trique qui lui donne une courbure n??gative constante permet de donner plan hyperbolique. Cette derni??re possibilit?? trouve une application dans la th??orie de la relativit?? restreinte dans le cas simplifi?? o?? il ya deux dimensions spatiales et une dimension temporelle. (Le plan hyperbolique est un type temps hypersurface en trois dimensions Espace de Minkowski.)

R??cup??r?? ?? partir de " http://en.wikipedia.org/w/index.php?title=Plane_(geometry)&oldid=197517431 "