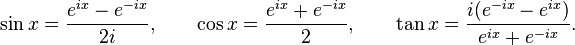Trigonom??trie
?? propos de ce ??coles s??lection Wikipedia
Les articles de cette s??lection ??coles ont ??t?? organis??s par sujet du programme d'??tudes gr??ce aux b??n??voles d'enfants SOS. SOS Children travaille dans 45 pays africains; pouvez-vous aider un enfant en Afrique ?

| Trigonom??trie |
|---|
| Histoire Usage Fonctions G??n??ralis?? Fonctions inverses Pour en savoir plus |
| R??f??rence |
| Identit??s Constantes pr??cises Tables trigonom??triques |
| Lois et th??or??mes |
| Loi des sinus Loi des cosinus Loi des tangentes Loi de cotangentes Th??or??me de Pythagore |
| Calcul |
| Substitution trigonom??trique Int??grales de fonctions D??riv??es des fonctions Int??grales de fonctions inverses |
Trigonom??trie (de grec trigōnon ??triangle?? + Metron "mesure") est une branche de math??matiques qui ??tudie les triangles et les relations entre les longueurs de leurs c??t??s et les angles entre les c??t??s. Trigonom??trie d??finit les fonctions trigonom??triques , qui d??crivent ces relations et ont applicabilit?? ?? des ph??nom??nes cycliques, comme les vagues. Le champ a ??volu?? au cours du troisi??me si??cle avant JC comme une branche de la g??om??trie largement utilis?? pour les ??tudes astronomiques. Il est aussi le fondement de la pratique de l'art arpentage.
bases de trigonom??trie sont souvent enseign??es dans l'??cole soit comme un cours s??par?? ou dans le cadre d'un Bien s??r precalculus. Les fonctions trigonom??triques sont omnipr??sents dans certaines parties de math??matiques pures et math??matiques appliqu??es telles que analyse de Fourier et la ??quation d'onde, qui sont ?? leur tour indispensables ?? de nombreuses branches de la science et de la technologie. Sph??riques ??tudes de trigonom??trie triangles sur sph??res , surfaces de constante positive courbure, en g??om??trie elliptique. Il est fondamental pour l'astronomie et la navigation. Trigonom??trie sur des surfaces ?? courbure n??gative fait partie de G??om??trie hyperbolique.
Histoire

Sum??riens astronomes introduits mesure d'angle, en utilisant une division de cercles en 360 degr??s. Eux et leurs successeurs les Babyloniens ont ??tudi?? les rapports des c??t??s des triangles semblables et ont d??couvert quelques propri??t??s de ces rapports, mais ne ont pas le transformer en une m??thode syst??matique pour trouver c??t??s et les angles des triangles. Le ancienne Nubiens utilis?? une m??thode similaire. Les anciens Grecs transform?? la trigonom??trie en une science ordonn??e.
Classique Math??maticiens grecs (tels que Euclide et d'Archim??de ) ont ??tudi?? les propri??t??s de les accords et les angles inscrits dans les cercles, et prouv?? th??or??mes qui sont ??quivalents ?? des formules trigonom??triques modernes, m??me se ils les ont pr??sent??s g??om??triquement plut??t que alg??brique. Claude Ptol??m??e ??tendus sur Accords Hipparque dans un cercle dans son Almageste. Le moderne fonction sinus a ??t?? d??fini dans le premier Surya Siddhanta, et ses propri??t??s ont encore ??t?? document??s par le 5??me si??cle math??maticien indien et astronome Aryabhata. Ces ??uvres grecques et indiennes ont ??t?? traduits et ??largis par math??maticiens islamiques m??di??vaux. Par le 10??me si??cle, les math??maticiens islamiques ??taient en utilisant tous les six fonctions trigonom??triques, avaient totalis??es leurs valeurs, et ont ??t?? les appliquer ?? des probl??mes de g??om??trie sph??rique. A peu pr??s au m??me moment, Math??maticiens chinois ont d??velopp?? la trigonom??trie ind??pendamment, bien que ce ne ??tait pas un champ d'??tude important pour eux. Connaissance des fonctions et des m??thodes trigonom??triques atteint l'Europe via Les traductions des ??uvres d'latine Astronomes persans et arabes tels que Al Battani et Nasir al-Din al-Tusi. Un des premiers travaux sur la trigonom??trie par un math??maticien europ??enne est Triangulis De par le 15??me si??cle allemand math??maticien Regiomontanus. Trigonom??trie ??tait encore si peu connu en Europe 16??me si??cle que Nicolas Copernic a consacr?? deux chapitres de Des r??volutions des sph??res c??lestes ?? expliquer ses concepts de base.
Pouss?? par les exigences de la navigation et le besoin croissant de cartes pr??cises des grandes r??gions, la trigonom??trie a grandi dans une branche importante des math??matiques. Pitiscus ??tait le premier ?? utiliser le mot, la publication de son Trigonometria en 1595. Gemma Frisius d??crit pour la premi??re fois le proc??d?? de triangulation utilis?? encore aujourd'hui dans l'arpentage. Ce ??tait Leonhard Euler qui ont pleinement int??gr?? nombres complexes dans la trigonom??trie. Les travaux de James Gregory dans le 17??me si??cle et Colin Maclaurin au 18??me si??cle ??tait influent dans le d??veloppement de la s??rie trigonom??trique. Toujours dans le 18??me si??cle, Brook Taylor d??fini le grand s??rie de Taylor .
Vue d'ensemble

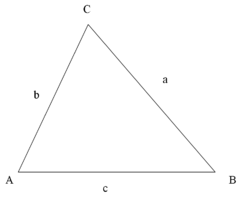
Si une angle d'un triangle est de 90 degr??s et l'un des autres angles est connue, la troisi??me est ainsi fix??, parce que les trois angles d'un triangle se additionnent ?? 180 degr??s. Les deux angles aigus donc ajouter jusqu'?? 90 degr??s: ils sont angles compl??mentaires. Le forme d'un triangle est compl??tement d??termin??, ?? l'exception de similarit??, par les angles. Une fois que les angles sont connus, le rapports des c??t??s sont d??termin??s, ind??pendamment de la taille globale du triangle. Si la longueur de l'un des c??t??s est connu, les deux autres sont d??termin??s. Ces ratios sont donn??s par les suivantes fonctions trigonom??triques de l'angle connu A, o?? a, b et c se r??f??rent ?? la longueur des c??t??s de la figure ci-jointe:
- Fonction sinus (sin), d??fini comme le rapport du c??t?? oppos?? ?? l'angle de la hypot??nuse.
- Cosinus fonction (cos), d??fini comme le rapport de la jambe adjacent ?? l'hypot??nuse.
- Tangent fonction (tan), d??fini comme le rapport de la jambe oppos??e ?? la jambe adjacente.
L'hypot??nuse est le c??t?? oppos?? ?? l'angle de 90 degr??s dans un triangle rectangle; ce est le c??t?? le plus long du triangle, et l'un des deux c??t??s adjacents ?? l'angle A. La jambe est adjacent de l'autre c??t?? qui est adjacent ?? l'angle A. Le c??t?? oppos?? est le c??t?? qui est oppos?? ?? l'angle A. Les termes perpendiculaires et la base sont parfois utilis??s pour les c??t??s oppos??s et adjacents respectivement. De nombreux anglophones trouvent qu'il est facile de se rappeler ce que les c??t??s du triangle rectangle sont ??gales ?? sinus, cosinus, tangente ou, en m??morisant le mot SOH-CAH-TOA (voir ci-dessous mn??moniques ).
Le inverses de ces fonctions sont nomm??s la cos??cante (csc ou COSEC), s??cant (s), et cotangent (b??b??), respectivement:
Le fonctions inverses sont appel??s l'arcsinus, arccosinus et arctangente, respectivement. Il existe des relations entre ces fonctions arithm??tiques, qui sont connus en tant que identit??s trigonom??triques. Le cosinus, cotangente, et cosecant sont ainsi nomm??s parce qu'ils sont respectivement le sinus, tangente, et s??cante de l'angle compl??mentaire en abr??g?? "coop??ration".
Gr??ce ?? ces fonctions, on peut r??pondre ?? pratiquement toutes les questions au sujet de triangles arbitraires en utilisant la loi des sinus et de la loi des cosinus. Ces lois peuvent ??tre utilis??s pour calculer les angles restants et les c??t??s d'un triangle, d??s que les deux faces et leur angle inclus ou deux angles et un c??t?? ou les trois c??t??s sont connus. Ces lois sont utiles dans toutes les branches de la g??om??trie, puisque chaque polygone peut ??tre d??crit comme une combinaison fini de triangles.
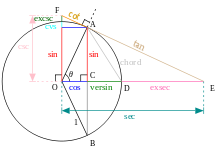
??tendre les d??finitions
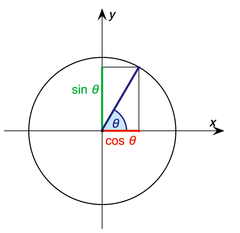
Les d??finitions ci-dessus se appliquent ?? des angles entre 0 ?? et 90 ?? (0 et π / 2 radians ) uniquement. En utilisant le cercle unit??, on peut les ??tendre ?? tous les arguments positifs et n??gatifs (voir fonction trigonom??trique ). Les fonctions trigonom??triques sont p??riodique, avec une p??riode de 360 degr??s ou 2π radians. Cela signifie que leurs valeurs r??p??ter ?? ces intervalles. Les fonctions de tangente et cotangente ont ??galement une p??riode plus courte, de 180 ?? ou π radians.
Les fonctions trigonom??triques peuvent ??tre d??finies par d'autres moyens en plus des d??finitions g??om??triques ci-dessus, en utilisant des outils de calcul et s??rie infinie. Avec ces d??finitions, les fonctions trigonom??triques peuvent ??tre d??finis pour des nombres complexes . La fonction exponentielle complexe est particuli??rement utile.
Voir Euler et Les formules de De Moivre.

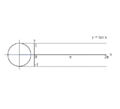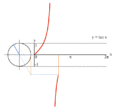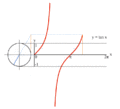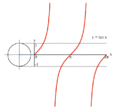
processus de graphique de y = sin (x) en utilisant un cercle unit??.
processus de graphique de y = tan (x) en utilisant un cercle unit??.
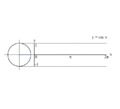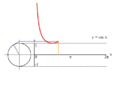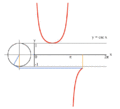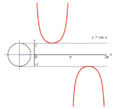
processus de graphique de y = csc (x) en utilisant un cercle unit??.
Mn??motechnique
Une utilisation courante de mn??moniques est de se souvenir des faits et des relations dans la trigonom??trie. Par exemple, les sinus, cosinus, tangentes et les ratios dans un triangle rectangle peuvent ??tre rappel??s en les repr??sentant comme des cha??nes de lettres. Par exemple, un mn??monique pour les anglophones est SOH-CAH-TOA:
- S ine = O pposite ?? H ypotenuse
- C = A Osine djacent ?? H ypotenuse
- T = O angent pposite ?? Un djacent
Une fa??on de rappeler les lettres est de les sonder phon??tiquement (c.-??-SOH-CAH-TOA, qui se prononce ??remorque soi-kə- '-Euh'). Une autre m??thode consiste ?? ??largir les lettres dans une phrase, comme ??S ome O ld H ippy C aught A utre H ippy T rippin 'O n A cid".
Calcul des fonctions trigonom??triques
Les fonctions trigonom??triques ont ??t?? parmi les premi??res utilisations pour tables math??matiques. Ces tableaux ont ??t?? incorpor??es dans les manuels de math??matiques et les ??l??ves ont appris ?? rechercher des valeurs et comment interpoler entre les valeurs indiqu??es pour obtenir une plus grande pr??cision. r??gles de chute avait ??chelles sp??ciales pour les fonctions trigonom??triques.
Aujourd'hui calculatrices scientifiques ont des boutons pour calculer les principales fonctions trigonom??triques (sin, cos, tan, et parfois cis et leurs inverses. La plupart permettent un choix de m??thodes de mesure d'angle: degr??s, radians et, parfois, grad. La plupart des ordinateurs langages de programmation fournissent des biblioth??ques de fonctions qui comprennent les fonctions trigonom??triques. Le point de mat??riel de l'unit?? int??gr??e dans les microprocesseurs utilis??s dans la plupart des ordinateurs personnels ont des instructions int??gr??es pour le calcul de fonctions trigonom??triques flottante.
Applications de la trigonom??trie

Il ya un nombre ??norme d'utilisations de la trigonom??trie et les fonctions trigonom??triques. Par exemple, la technique de triangulation est utilis?? dans l'astronomie pour mesurer la distance des ??toiles proches, dans la g??ographie pour mesurer les distances entre les points de rep??re, et syst??mes de navigation par satellite. Les fonctions sinus et cosinus sont essentiels ?? la th??orie de la des fonctions p??riodiques, tels que ceux que d??crivent sonores et lumineuses ondes.
Les champs qui utilisent des fonctions de trigonom??trie ou trigonom??triques comprennent l'astronomie (en particulier pour localiser les positions apparentes des objets c??lestes, dans lequel trigonom??trie sph??rique est essentiel) et donc Navigation (sur les oc??ans, dans les avions, et dans l'espace), th??orie de la musique, l'acoustique, l'optique , l'analyse des march??s financiers, l'??lectronique , la th??orie des probabilit??s , les statistiques , la biologie , imagerie m??dicale ( tomodensitom??trie et ??chographie), pharmacie, la chimie , la th??orie des nombres (et donc la cryptologie ), sismologie, la m??t??orologie , l'oc??anographie , de nombreuses sciences physiques , la terre arpentage et g??od??sie, l'architecture , phon??tique, ??conomie , g??nie ??lectrique , g??nie m??canique , g??nie civil , infographie, cartographie, cristallographie et le d??veloppement de jeux.
Identit??s standard
Les identit??s sont ces ??quations qui d??tiennent vrai pour ne importe quelle valeur.
formules de transformation d'angle
Formules communes
Certaines ??quations impliquant des fonctions trigonom??triques sont vraies pour tous les angles et sont connus comme des identit??s trigonom??triques. Certaines identit??s assimilent une expression ?? une expression diff??rente impliquant les m??mes angles. Ils sont ??num??r??s dans Liste des identit??s trigonom??triques. Triangle identit??s qui relient les c??t??s et les angles d'un triangle donn?? sont r??pertori??s ci-dessous.
Dans les identit??s suivantes, A, B et C sont les angles d'un triangle et a, b et c sont les longueurs des c??t??s du triangle en regard des angles respectifs.
Loi des sinus
Le loi des sinus (aussi connu comme la ??r??gle sine") pour un Etats triangle arbitraires:
o?? R est le rayon de la cercle circonscrit du triangle:
Une autre loi impliquant sinus peut ??tre utilis?? pour calculer l'aire d'un triangle. Compte tenu deux c??t??s et l'angle entre les c??t??s, la surface du triangle est:
Loi des cosinus
Le loi des cosinus (connus sous le nom de la formule du cosinus, ou la ??r??gle des cos") est une extension du th??or??me de Pythagore aux triangles arbitraires:
ou de mani??re ??quivalente:
Loi des tangentes
Le la loi des tangentes:
La formule d'Euler
La formule d'Euler, qui stipule que  , Produit les suivants analytiques identit??s pour sinus, cosinus et tangente en termes de e et l' unit?? imaginaire i:
, Produit les suivants analytiques identit??s pour sinus, cosinus et tangente en termes de e et l' unit?? imaginaire i:

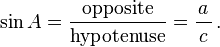
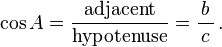
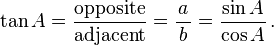
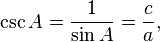
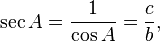
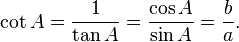
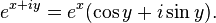
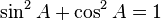
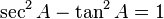

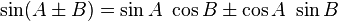
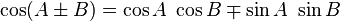
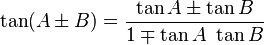
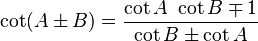
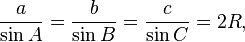
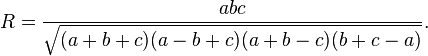

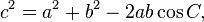
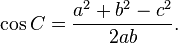
![\ Frac {ab} {a + b} = \ frac {\ tan \ left [\ frac {1} {2} (AB) \ right]} {\ tan \ left [\ frac {1} {2} (A + B) \ right]}](../../images/2161/216156.png)