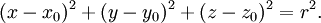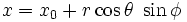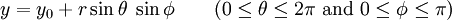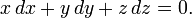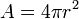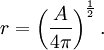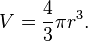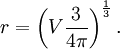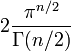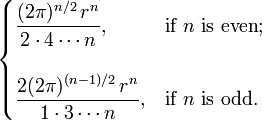Sph??re

Contexte des ??coles Wikip??dia

SOS croit que l'??ducation donne une meilleure chance dans la vie des enfants dans le monde en d??veloppement aussi. Le parrainage d'enfants aide les enfants un par un http://www.sponsor-a-child.org.uk/ .

Une sph??re.

Une sph??re est une sym??trie g??om??trique objet. Dans l'usage non math??matique, le terme est utilis?? pour se r??f??rer soit ?? un tour bille ou ?? son bidimensionnelle surface. En math??matiques , une sph??re est l'ensemble de tous les points de un espace tridimensionnel (R ³⁾ qui sont ?? une distance r ?? partir d'un point fixe de l'espace, o?? r est un positif nombre r??el appel?? le rayon de la sph??re. Ainsi, en trois dimensions, une sph??re math??matique est consid??r?? comme une surface sph??rique ?? deux dimensions noy?? dans un espace tridimensionnel, plut??t que le volume contenu ?? l'int??rieur (ce qui math??maticiens place d??crire comme un balle). Le point fixe est appel?? le centre ou du centre, et ne fait pas partie de la sph??re elle-m??me. Le cas particulier de r = 1 est appel?? sph??re unit??.

Cet article traite de la notion math??matique d'une sph??re. En physique , une sph??re est un objet (g??n??ralement id??alis?? pour des raisons de simplicit??) capable d'entrer en collision ou empilage avec d'autres objets qui occupent l'espace.

Equations dans R ³

Dans la g??om??trie analytique , une sph??re de centre (x _0, y _0, z ₀₎ et de rayon r est le lieu des points (x, y, z) de telle sorte que

$(X - x_0) ^ 2 + (y - Y_0) ^ 2 + (z - z_0) ^ 2 = r ^ 2.$

Les points sur la sph??re de rayon r peuvent ??tre param??tr??s via

$x = x 0 + r \ cos \ theta \; \ Sin \ phi$

$y = Y_0 + r \ sin \ theta \; \ Sin \ phi \ qquad (0 \ leq \ theta \ leq 2 \ pi \ mbox {et} 0 \ leq \ phi \ leq \ pi) \,$

$z = z_0 + r \ cos \ phi \,$

(Voir aussi les fonctions trigonom??triques et coordonn??es sph??riques ).

Une sph??re de rayon centr?? quelconque ?? l'origine est d??crite de la mani??re suivante ??quation diff??rentielle :

$x \, dx + y \, dy + z \, dz = 0.$

Cette ??quation refl??te le fait que les vecteurs position et de vitesse d'un point voyageant sur la sph??re sont toujours orthogonales entre elles.

Le zone de surface d'une sph??re de rayon r est

$A = 4 \ pi r ^ 2 \,$

donc le rayon de surface sp??cifique est

$r = \ left (\ frac {A} {4 \ pi} \ right) ^ \ frac {1} {2}.$

Son volumique est

$V = \ frac {4} {3} \ pi r ^ 3.$

de sorte que le rayon de volume est

$r = \ left (V \ frac {3} {4 \ pi} \ right) ^ \ frac {1} {3}.$

La sph??re a la plus petite aire de surface entre les surfaces entourant un volume donn?? et il renferme le plus grand volume parmi toutes les surfaces ferm??es avec une aire de surface donn??e. Pour cette raison, la sph??re appara??t dans la nature: par exemple des bulles et des gouttelettes d'eau sont ?? peu pr??s sph??rique, car la tension de surface minimise localement surface.

Une image de l'un des domaines les plus pr??cis jamais cr???? par l'homme, comme il r??fracte l'image d'Einstein dans le fond. Cette sph??re a un quartz fondu gyroscope pour la Exp??rience Gravity Probe B qui diff??re dans la forme d'une sph??re parfaite de pas plus de 40 atomes d'??paisseur. On pense que seulement ??toiles ?? neutrons sont plus lisses. Il a ??t?? annonc?? sur 15 Juin 2007, que australiens scientifiques ont l'intention de faire m??me des sph??res plus parfaits, pr??cise ?? 35 millioni??mes de millim??tre, dans le cadre d'une chasse internationale pour trouver une nouvelle norme mondiale kg .

Le circonscrit pour un cylindre donn?? sph??re a un volume qui est 3/2 fois le volume de la sph??re, et ??galement la partie incurv??e a une aire de surface qui est ??gale ?? la surface de la sph??re. Ce fait, ainsi que les volume et de surface formules indiqu??es ci-dessus, ??tait d??j?? connu d'Archim??de .

Une sph??re peut ??galement ??tre d??finie comme la surface form??e par la rotation d'un cercle pr??s ne importe quel diam??tre . Si le cercle est remplac??e par une ellipse , et en rotation autour de l'axe principal, la forme allong??e devient sph??ro??de, en rotation autour de l'axe mineur, un sph??ro??de aplati.

Terminologie

Les paires de points d'une sph??re qui se trouvent sur une droite passant par son centre sont appel??s les points aux antipodes. Un grand cercle est un cercle sur la sph??re qui a le m??me centre et rayon que la sph??re, et par cons??quent, il se divise en deux parties ??gales. La distance la plus courte entre deux points non-antipodes distinctes sur la surface et mesur??e le long de la surface, est sur le grand cercle unique, en passant par les deux points.

Si un point particulier sur une sph??re est d??sign?? comme son p??le nord, alors le point antipode correspondante est appel??e le p??le sud et l' ??quateur est le grand cercle qui est ??quidistant pour eux. Les grands cercles ?? travers les deux p??les sont appel??es lignes (ou m??ridiens) du la longitude et la ligne reliant les deux p??les est appel?? le axe de rotation. Les cercles sur la sph??re qui sont parall??les ?? l'??quateur sont des lignes de latitude . Cette terminologie est ??galement utilis?? pour les organismes astronomiques tels que la plan??te Terre , m??me si elle ne est ni sph??rique ni m??me sph??ro??de (voir g??o??de).

Une sph??re est divis??e en deux h??misph??res ??gales par ne importe quel plan qui passe par son centre. Si deux plans se coupant traversent son centre, puis ils vont diviser la sph??re en quatre lunes ou biangles, dont les sommets co??ncident tous avec les points antipodes couch?? sur la ligne d'intersection des plans.

G??n??ralisation ?? d'autres dimensions

Sph??res peuvent ??tre g??n??ralis??s ?? des espaces de toute dimension. Pour tout entier naturel n, un n -sphere, souvent ??crit S ^n, est l'ensemble des points dans (n 1) l'espace euclidien de dimension qui sont ?? une distance r fixe ?? partir d'un point central de cet espace, o?? r est , comme pr??c??demment, un nombre r??el positif. En particulier:

une 0-sph??re est une paire de points d'extr??mit?? d'un intervalle (- r, r) de la ligne r??elle
une sph??re 1 est un cercle de rayon r
2-sph??re est une sph??re ordinaire
une 3-sph??re est une sph??re dans l'espace euclidien ?? 4 dimensions.

Sph??res pour n> 2 sont parfois appel??s hypersph??res.

Le n -sphere de rayon unit?? centr?? ?? l'origine est not??e S ⁿ et est souvent d??sign?? comme ??le?? n -sphere. Notez que la sph??re ordinaire 2-sph??re, car ce est une surface deux dimensions.

La surface de la (n-1) -sphere de rayon 1 est

$2 \ frac {\ pi ^ {n / 2}} {\ Gamma (n / 2)}$

o?? Γ (z) est d'Euler Fonction Gamma.

Une autre formule de surface est

$\ Begin {cas} \ displaystyle \ frac {(2 \ pi) ^ {n / 2} \, r ^ {n-1}} {2 \ cdot 4 \ cdots (n-2)}, et \ text {if } n \ text {} est encore; \\ \\ \ Displaystyle \ frac {2 (2 \ pi) ^ {(n-1) / 2} \, r ^ {n-1}} {1 \ cdot 3 \ cdots (n-2)}, et \ text {if} n \ text {} est impair. \ end {} cas$

et le volume est en dehors des heures de surface 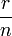${R \ over n}$ ou

$\ Begin {cas} \ displaystyle \ frac {(2 \ pi) ^ {n / 2} \, r ^ n} {2 \ cdot 4 \ cdots n}, et \ text {if} n \ text {} est encore ; \\ \\ \ Displaystyle \ frac {2 (2 \ pi) ^ {(n-1) / 2} \, r ^ n} {1 \ cdot 3 \ cdots n}, et \ text {if} n \ text {} est ??trange. \ end {} cas$

G??n??ralisation aux espaces m??triques

Plus g??n??ralement, dans un espace m??trique (E, D), la sph??re de centre et de rayon x

est l'ensemble des points y tels que d (x, y) = r.

Si le centre est un point distingu?? consid??r?? comme origine de E, comme dans un espace norm??, il ne est pas mentionn?? dans la d??finition et la notation. Il en va de m??me pour le rayon se il est pris ??gal ?? un, comme dans le cas d'un sph??re unit??.

Contrairement ?? un boule, une sph??re peut ??tre un ensemble vide, m??me pour un grand rayon. Par exemple, dans Z ⁿ avec M??trique euclidienne, une sph??re de rayon r est non vide seulement si R ² peut se ??crire comme somme des carr??s de nombres entiers n.

Topologie

En topologie , un n -sphere est d??fini comme un espace hom??omorphe ?? la limite d'une (N + 1) -boule; Ainsi, il est hom??omorphe ?? l'euclidien n -sphere, mais peut-??tre d??pourvu de son m??trique.

une 0-sph??re est une paire de points avec le topologie discr??te
une sph??re 1 est un cercle ( jusqu'?? hom??omorphisme ); Ainsi, par exemple, (de l'image) toute noeud est une sph??re 1
2-sph??re est une sph??re ordinaire ( jusqu'?? hom??omorphisme ); Ainsi, par exemple, toute sph??ro??de est une sph??re de dimension 2

Le n -sphere est not??e S ^n. Il se agit d'un exemple d'un compact collecteur topologique sans limite. Une sph??re ne doit pas ??tre lisse ; si elle est lisse, il ne est pas n??cessairement diff??omorphe ?? la sph??re euclidienne.

Le Heine-Borel th??or??me implique qu'un euclidien n -sphere est compact. La sph??re est l'image inverse d'un d'un point fix?? en vertu de la fonction continue || x ||. Par cons??quent, la sph??re est un ferm??. S ⁿ est ??galement d??limit??e. Par cons??quent, il est compact.

G??om??trie sph??rique

Grand cercle sur une sph??re

Les ??l??ments de base de la g??om??trie plane sont points et lignes . Sur la sph??re, les points sont d??finis dans le sens habituel, mais l'analogue de "ligne" peuvent ne pas se manifester imm??diatement. Si l'on mesure par une longueur d'arc constate que la voie la plus courte reliant deux points situ??s enti??rement dans la sph??re est un segment de la grand cercle contenant les points; voir g??od??sique. Beaucoup de th??or??mes de la g??om??trie classique vrai pour ceci g??om??trie sph??rique ainsi, mais beaucoup ne (voient pas postulat des parall??les). En trigonom??trie sph??rique, angles sont d??finis entre les grands cercles. Ainsi trigonom??trie sph??rique est diff??rent de l'ordinaire la trigonom??trie ?? bien des ??gards. Par exemple, la somme des angles int??rieurs d'un triangle sph??rique d??passe 180 degr??s. De plus, deux quelconques triangles sph??riques similaires sont congruents.

Onze propri??t??s de la sph??re

Dans leur g??om??trie du livre et l'imagination David Hilbert et Stephan Cohn-Vossen d??crire onze propri??t??s de la sph??re et de discuter si ces propri??t??s d??terminent uniquement la sph??re. Plusieurs propri??t??s d??tiennent pour le plan qui peut ??tre consid??r?? comme une sph??re de rayon infini. Ces propri??t??s sont les suivantes:

Les points de la sph??re sont tous ?? la m??me distance d'un point fixe. En outre, le rapport de la distance de ses points ?? partir de deux points fixes est constante.
La premi??re partie est la d??finition usuelle de la sph??re et il d??termine de fa??on unique. La deuxi??me partie peut ??tre d??duit facilement et suit un m??me r??sultat de Apollonius de Perge pour le cercle . Cette seconde partie est aussi valable pour l' avion .
Les sections de contours et de platanes de la sph??re sont des cercles.
Cette propri??t?? d??finit la sph??re unique.
La sph??re a une largeur constante et la circonf??rence constante.
La largeur d'une surface est la distance entre les paires de plans parall??les tangents. Il existe de nombreuses autres surfaces convexes ferm??s qui ont une largeur constante, par exemple Le t??tra??dre de Meissner. La circonf??rence d'une surface est la circonf??rence de la limite de sa projection orthogonale sur un plan. Il peut ??tre prouv?? que chacune de ces propri??t??s implique l'autre.

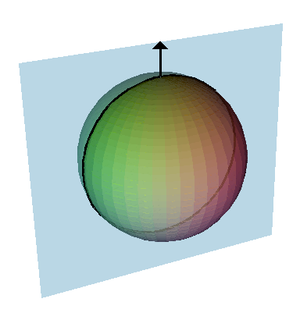Un vecteur normal ?? une sph??re, un plan normal et sa section normale. La courbure de la courbe d'intersection est la courbure transversale. Pour chaque section de la sph??re normale par un point donn?? sera un cercle de m??me rayon, le rayon de la sph??re. Cela signifie que chaque point de la sph??re sera un point ombilical.
Tous les points d'une sph??re sont ombilics.
?? tout moment sur une surface que nous pouvons trouver un direction normale qui est perpendiculaire ?? la surface, de la sph??re sur ces lignes rayonnantes ?? partir du centre de la sph??re. L'intersection d'un plan contenant la normale ?? la surface formera une courbe appel??e une section normale et la courbure de cette courbe est la courbure transversale. Pour la plupart des points sur une surfaces diff??rentes sections auront diff??rentes courbures, les valeurs maximales et minimales de ceux-ci sont appel?? courbures principales. Il peut ??tre prouv?? que ne importe quelle surface ferm??e aura au moins quatre points appel??s Le secteur ombilical. A un ombilic toutes les courbures transversales sont ??gales, en particulier le courbure principaux de sont ??gaux. Les points ombilical peuvent ??tre consid??r??s comme les points o?? la surface est ??troitement approch??e par une sph??re.
Pour la sph??re des courbures de toutes les sections normales sont ??gales, donc chaque point est un ombilic. La sph??re et le plan sont les seules surfaces avec cette propri??t??.
La sph??re ne poss??de pas une surface de centres.
Pour une section donn??e, il existe normalement un cercle dont la courbure est la m??me que la courbure en coupe, est tangente ?? la surface et dont le centre le long de lignes sur la ligne normale. Prenez les deux centre correspondant ?? la coupe maximum et minimum courbures Ils sont appel??s les points focaux, et l'ensemble de tous ces centres constitue la surface focale.
Pour la plupart des surfaces la surface focale forme deux feuilles dont chacun repr??sente une surface et qui viennent ensemble ?? des points ombilicaux. Il existe un certain nombre de cas particuliers. Pour canal surfaces une feuille forme une courbe et l'autre feuille est une surface; Pour c??nes, cylindres, tores et cyclides les deux feuilles forment des courbes. Pour la sph??re au centre de chaque cercle osculateur est au centre de la sph??re et la surface focale forme un seul point. Ce est une propri??t?? unique de la sph??re.
Tous les g??od??siques de la sph??re sont des courbes ferm??es.
G??od??siques sont des courbes sur une surface qui donnent la plus courte distance entre deux points. Ils sont g??n??ralisation du concept d'une ligne droite dans le plan. Pour la sph??re les g??od??siques sont des grands cercles. Il ya beaucoup d'autres surfaces avec cette propri??t??.
De tous les solides ayant un volume donn??, la sph??re est celui avec la plus petite aire de surface; de toutes les mati??res solides ayant une aire de surface donn??e, la sph??re est celle ayant le plus grand volume.
Ces propri??t??s d??finissent la sph??re unique. Ces propri??t??s peuvent ??tre vus par l'observation des bulles de savon. Une bulle de savon se enfermer un volume fixe et en raison de la tension de surface il va essayer de minimiser sa surface. Par cons??quent, une bulle de savon flottant libre sera approximativement une sph??re, des facteurs comme la gravit?? entra??nera une l??g??re distorsion.
La sph??re a la plus petite courbure moyenne totale entre tous les solides convexes avec une aire de surface donn??e.
Le courbure moyenne est la moyenne des deux courbures principales et que ceux-ci sont constants ?? tous les points de la sph??re est alors si la courbure moyenne.
La sph??re a courbure moyenne constante positive.
La sph??re est la seule surface sans bord ou singularit??s avec courbure moyenne constante positive. Il ya d'autres surfaces ?? courbure moyenne constante, le surfaces minimales ont z??ro courbure moyenne.
La sph??re a courbure gaussienne constante positive.
Courbure gaussienne est le produit des deux courbures principales. Ce est une propri??t?? intrins??que qui peut ??tre d??termin?? en mesurant la longueur et les angles et ne d??pend pas de la fa??on dont la surface est int??gr?? dans l'espace. Par cons??quent, le pliage d'une surface ne modifie pas la courbure gaussienne et d'autres surfaces avec une constante courbure gaussienne positive peut ??tre obtenu en coupant une petite fente dans la sph??re et le plier. Tous ces autres surfaces auraient fronti??res et la sph??re est la seule surface sans limite avec courbure gaussienne constante positive. Le pseudosph??re est un exemple d'une surface ?? courbure gaussienne n??gative constante.
La sph??re se transforme en elle-m??me par une famille ?? trois param??tres de mouvements rigides.
Consid??rons un lieu de sph??re unit?? ?? l'origine, une rotation autour de l'axe x, y ou z traceront la sph??re sur lui-m??me, en effet toute rotation autour d'une ligne passant par l'origine peut ??tre exprim??e comme une combinaison de rotations autour des trois axes de coordonn??es, voir Angles d'Euler. Ainsi, il ya une famille de trois des param??tres de rotations qui transforment la sph??re sur lui-m??me, ce est le groupe de rotation, SO (3). L'avion est le seul autre surface avec une famille de trois param??tres de transformations (translation le long de l'axe et la rotation autour de l'origine x et y). Cylindres circulaires sont les seules surfaces avec deux familles de param??tres de mouvements rigides et la surfaces de r??volution et h??lico??des sont les seules surfaces avec une famille ?? un param??tre.

R??cup??r?? ?? partir de " http://en.wikipedia.org/w/index.php?title=Sphere&oldid=198842305 "