
Volume
Saviez-vous ...
Les articles de cette s??lection ??coles ont ??t?? organis??s par sujet du programme d'??tudes gr??ce aux b??n??voles d'enfants SOS. Visitez le site Web d'enfants SOS au http://www.soschildren.org/
Le volume de tout solide, liquide ou gazeux est de savoir combien de trois espace de dimension qu'il occupe, souvent quantifi?? num??riquement. Figures unidimensionnelles (tels que des lignes ) et les formes ?? deux dimensions (par exemple, carr??s ) sont affect??s volume nul dans l'espace ?? trois dimensions.
Les volumes de formes droites tranchant et circulaires sont calcul??s ?? l'aide des formules arithm??tiques. Volumes d'autres formes courbes sont calcul??es en utilisant le calcul int??gral , en rapprochant l'organe donn?? avec une grande quantit?? de petits cubes ou concentrique coques cylindriques, et en ajoutant les volumes individuels de ces formes. Le volume d'objets de forme irr??guli??re peut ??tre d??termin??e par d??placement. Si un objet de forme irr??guli??re est moins dense que le fluide, vous aurez besoin d'un poids ?? attacher ?? l'objet flottant. Un poids suffisant fera l'objet ?? couler. Le volume final de l'objet inconnu peut ??tre trouv?? en soustrayant le volume de l'objet lourd ci-joint et le volume total du fluide d??plac??.
La g??n??ralisation de volume ?? un nombre arbitraire de dimensions est appel?? contenu. En g??om??trie diff??rentielle , le volume est exprim?? au moyen de la formulaire de volume.
Volume et la capacit?? sont parfois distingu??, avec une capacit?? utilis?? pour combien un conteneur peut contenir (avec des teneurs mesur??es couramment dans litres ou ses unit??s d??riv??es), et le volume ??tant combien d'espace un d??place de l'objet (g??n??ralement mesur??es en m??tres cubes ou de ses unit??s d??riv??es). Le volume d'un gaz dispers?? est la capacit?? de son contenant. Si plus de gaz est ajout?? ?? un r??cipient ferm??, le r??cipient se dilate soit (comme dans un ballon) ou la pression ?? l'int??rieur du r??cipient augmente.
Volume et la capacit?? se distinguent ??galement dans un cadre de gestion de la capacit??, o?? la capacit?? est d??finie comme le volume sur une p??riode de temps sp??cifi??e.
Le volume est un param??tre fondamental dans la thermodynamique et il est conjugu?? ?? pression.
| Variables conjugu??es de la thermodynamique | |
|---|---|
| Pression | Volume |
| ( Stress) | ( Strain) |
| Temp??rature | Entropy |
| Potentiel chimique | nombre de particules |
formules de volume
| Communes ??quations pour le volume: | ||
|---|---|---|
| Forme | ??quation | Variables |
| Un cube : | 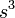 | s = longueur de ne importe quel c??t?? |
| Un rectangulaire prisme: | 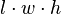 | L = L ongueur, w = w idth, h = h huit |
| Un cylindre (prisme circulaire): | 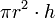 | r = rayon de face circulaire, h = hauteur |
| De pr??f??rence un prisme qui a une surface de section constante sur toute la hauteur **: | 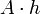 | A = aire de la base, h = hauteur |
| Une sph??re : | 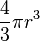 | r = rayon de sph??re qui est l' int??grale de la Surface d'une sph??re |
| Une ellipso??de: | 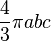 | a, b, c = demi-axes de l'ellipso??de |
| Un pyramide: | 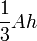 |
A = surface de la base, h = hauteur de la pyramide |
| Un c??ne (circulaire fond??e pyramide): | 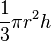 | r = rayon de cercle ?? la base, h = distance de la base au sommet |
| Tout chiffre ( calcul n??cessaire) | 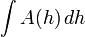 | h = la plus grande dimension de la figure, A (h) = aire de la section transversale perpendiculaire ?? h d??crite comme une fonction de la position le long de h. Cela fonctionne pour tout chiffre si sa section transversale peut ??tre d??termin??e ?? partir de h (peu importe si le prisme est inclin??e ou les sections changer de forme). ^ * |
(Les unit??s de volume d??pendent des unit??s de longueur - si les longueurs sont en m??tres, le volume sera en m??tres cubes, etc.)
Le volume d'un parall??l??pip??de est la valeur absolue de la triple produit scalaire des vecteurs de sous-tendant, ou de mani??re ??quivalente ?? la valeur absolue du d??terminant de la matrice correspondante.
Le volume de ne importe quel t??tra??dre , ??tant donn?? ses sommets A, B, C et D, est (1/6) ?? | det (A - B, B - C, C - D) |, ou toute autre combinaison de paires de sommets former une simplement connexe graphique.
Les mesures de volume: UK
Le Royaume-Uni est en cours syst??me m??trique et est de plus en plus l'aide de la Les unit??s de SI syst??me m??triques de volume, ce est- m??tre cube et litre. Cependant, certains anciens unit??s de volume sont toujours en degr??s d'utilisation variant:
Unit??s imp??riales de volume:
- Fluide UK onces, environ 28,4 ml (ce est ??gal au volume d'un avoirdupois onces d'eau sous certaines conditions)
- Royaume-Uni pinte = 20 onces liquides, soit environ 568 ml
- Royaume-Uni quarts = 40 onces ou deux pints1.137 L
- Royaume-Uni gallon = 4 quarts, ou exactement 4,546 09 L
Le quart est maintenant obsol??te et l'once liquide extr??mement rare. Le gallon est utilis?? uniquement ?? des fins de transport, (il est ill??gal pour l'essence et le diesel ?? ??tre vendus par le gallon). La pinte est la seule unit?? imp??riale qui est en usage quotidien, pour la vente de bi??re et de cidre (bouteille et la bi??re en conserve est principalement vendu en unit??s SI) et pour le lait (ce est aussi de plus en plus vendu en unit??s SI, principalement Litres) .
Les mesures de volume: la cuisson
Les mesures traditionnelles de cuisson pour le volume comprennent ??galement:
- cuill??re ?? caf?? = 1/6 US once liquide (environ 4,929 ml)
- = cuill??re ?? caf?? de 1/6 once liquide imp??riale (environ 4,736 ml)
- cuill??re ?? caf?? = 5 ml (m??trique)
- cuill??re ?? soupe = ?? US once liquide ou 3 cuill??res ?? caf?? (environ 14,79 ml)
- cuill??re ?? soupe = ?? once liquide imp??riale ou 3 cuill??res ?? caf?? (environ 14,21 ml)
- ?? soupe = 15 ml ou 3 cuiller??es ?? th?? (m??triques)
- cuill??re ?? soupe = 5 fluidrams (environ 17,76 ml) (Colombie)
- tasse = 8 onces liquides am??ricaines ou ?? US pinte liquide (environ 237 ml)
- tasse = 8 onces liquides imp??riales ou ?? litre de liquide (environ 227 ml)
- tasse = 250 ml (m??trique)
Relation ?? la densit??
La densit?? d'un objet est d??fini en tant que masse par unit?? de volume.
Le terme volume sp??cifique est utilis?? pour le volume divis?? par la masse. Ceci est le r??ciproque de la densit?? de masse , exprim??e en unit??s telles que m??tres cubes par kilogramme (m?? ?? kg -1).
Volume formule d??rivation
| Forme | Volume formule d??rivation |
|---|---|
| Sph??re | Le volume d'une sph??re est l' int??grale de plaques circulaires de largeur infinit??simales 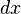 . . Le calcul pour le volume d'une sph??re de centre 0 et de rayon r est le suivant.
|
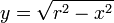
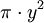
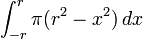
 par
par 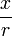 , De sorte que les limites deviennent solidaires -1 et +1, on obtient
, De sorte que les limites deviennent solidaires -1 et +1, on obtient 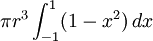
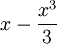
![\ Pi r ^ 3 \ cdot [1-1 / 3 - (- 1 + 1/3)]](../../images/206/20619.png) =
= 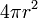 . Le volume de la sph??re est constitu??e de couches de plaques sph??riques infinit??simales, et le volume de la sph??re est ??gale ??
. Le volume de la sph??re est constitu??e de couches de plaques sph??riques infinit??simales, et le volume de la sph??re est ??gale ?? 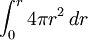 =
= 