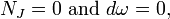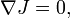G??om??trie diff??rentielle

G??om??trie diff??rentielle est une math??matique discipline qui utilise les m??thodes de diff??rentiel et int??gral calcul pour ??tudier les probl??mes de g??om??trie . La th??orie de l'avion et de l'espace et les courbes de surfaces en trois dimensions espace euclidien forment la base de son d??veloppement initial dans le XVIIIe et XIXe si??cles. Depuis la fin du XIXe si??cle, la g??om??trie diff??rentielle a grandi dans un champ concern?? plus g??n??ralement avec des structures g??om??triques sur vari??t??s diff??rentiables. Il est ??troitement apparent?? avec topologie diff??rentielle et avec les aspects g??om??triques de la th??orie des ??quations diff??rentielles . La preuve de la Conjecture de Poincar?? en utilisant les techniques de Flot de Ricci a d??montr?? la puissance de l'approche diff??rentielle g??om??trique aux questions de topologie et a soulign?? le r??le important jou?? par les m??thodes analytiques.

Branches de la g??om??trie diff??rentielle

La g??om??trie de Riemann

??tudes de g??om??trie de Riemann Vari??t??s riemanniennes, vari??t??s lisses avec une m??trique riemannienne, une notion de distance exprim??e au moyen d'un d??finie positive forme bilin??aire sym??trique d??finie sur l'espace tangent en chaque point. La g??om??trie de Riemann g??n??ralise la g??om??trie euclidienne aux espaces qui ne sont pas n??cessairement plane, bien qu'ils ressemblent encore l' espace euclidien ?? chaque point "infiniment", ce est ?? dire dans le premier ordre d'approximation. Divers concepts bas??s sur la longueur, comme le longueur de l'arc de courbes , la zone des r??gions planes, et le volume de solides admettent tous analogues naturels dans la g??om??trie de Riemann. La notion de d??riv??e directionnelle d'une fonction ?? partir de la Fonction de plusieurs variables est prolong??e dans la g??om??trie de Riemann ?? la notion d'un d??riv??e covariante d'un tenseur. De nombreux concepts et techniques d'analyse et ??quations diff??rentielles ont ??t?? g??n??ralis??es ?? l'??tablissement des vari??t??s riemanniennes.

Une distance de pr??servation diff??omorphisme entre vari??t??s riemanniennes est appel?? isom??trie. Cette notion peut ??galement ??tre d??finie localement, ce est ?? dire pour les petits quartiers de points. Les deux courbes r??guli??res sont localement isom??trique. Cependant, Theorema egregium de Gauss d??j?? montr?? que pour les surfaces, l'existence d'une isom??trie locale impose des conditions de compatibilit?? fortes sur leurs param??tres: la Courbures gaussiennes aux points correspondants doivent ??tre les m??mes. En dimension sup??rieure, le Tenseur de Riemann est un important invariant ponctuelle associ??e ?? une vari??t?? riemannienne qui mesure ?? quel point il est d'??tre plat. Une classe importante de vari??t??s riemanniennes est form?? par la Espaces sym??triques de Riemann, dont la courbure est constante. Ils sont le plus proche du plan ??ordinaire?? et l'espace consid??r?? et dans euclidienne g??om??trie non-euclidienne.

g??om??trie pseudo-riemannienne

g??om??trie pseudo-riemannienne g??n??ralise la g??om??trie de Riemann ?? l'affaire dans laquelle la tenseur m??trique ne est pas n??cessairement d??finie positive. Un cas particulier de ceci est un Collecteur de Lorentz qui est la base math??matique de Einstein de la th??orie de la relativit?? g??n??rale de gravit?? .

G??om??trie Finsler

G??om??trie Finsler a le collecteur Finsler que l'objet principal de l'??tude - ce est une vari??t?? diff??rentielle avec un Finsler m??trique, soit une Banach norme d??finie sur chaque espace tangent. Une m??trique Finsler est une structure beaucoup plus g??n??ral que une m??trique riemannienne. Structure Finsler sur une vari??t?? M est une fonction F: M → T [0, ∞) de sorte que:

1. F (x, my) = MF (x, y) pour tout x, y dans T M,
2. F est infiniment diff??rentiable en T M - {0},
3. La Hesse verticale de F ² est d??finie positive.

G??om??trie symplectique

G??om??trie symplectique est l'??tude des vari??t??s symplectiques. Une vari??t?? presque symplectique est une vari??t?? diff??rentiable ??quip?? d'un variant doucement non d??g??n??r??e antisym??trique forme bilin??aire sur chaque espace tangent, soit un non d??g??n??r??e 2- forme ω, appel?? la forme symplectique. Une vari??t?? symplectique est une vari??t?? presque symplectique pour lesquels la forme symplectique ω est ferm??e: d ω = 0.

Un diff??omorphisme entre deux vari??t??s symplectiques qui pr??serve la forme symplectique est appel?? symplectomorphisme. Non d??g??n??r??e antisym??trique formes bilin??aires ne peuvent exister, m??me sur les espaces vectoriels de dimension, de sorte que les vari??t??s symplectiques ont n??cessairement m??me dimension. En dimension 2, une vari??t?? symplectique est juste un surface dot??e d'une forme de la zone et un symplectomorphisme est un diff??omorphisme de la zone de pr??servation. Le espace de phase d'un syst??me m??canique est une vari??t?? symplectique et ils ont fait une apparition implicite d??j?? dans le travail de Lagrange sur m??canique analytique et plus tard dans Jacobi et Hamilton la formulation de la m??canique classique.

En revanche avec la g??om??trie de Riemann, o?? le courbure offre un invariant locale de vari??t??s riemanniennes, Th??or??me de Darboux stipule que toutes les vari??t??s symplectiques sont localement isomorphes. Les seuls invariants d'une vari??t?? symplectique sont de nature mondiale et les aspects topologiques jouent un r??le de premier plan en g??om??trie symplectique. Le premier r??sultat en topologie symplectique est probablement le Th??or??me de Poincar??-Birkhoff, conjectur?? par Henri Poincar?? et prouv?? par George Birkhoff en 1912. Il affirme que si une zone en pr??servant la carte d'un annulaires rebondissements chaque composante de bord dans des directions oppos??es, puis la carte a au moins deux points fixes.

G??om??trie de contact

Contactez g??om??trie, traite de certains collecteurs de dimension impaire. Il est proche de la g??om??trie symplectique et, comme ce dernier, il est originaire dans les questions de la m??canique classique. Structure de contact sur une (n 2 1) de dimension vari??t?? M est donn??e par un champ de hyperplan H de la lisse faisceau tangent qui est aussi loin que possible de leur association avec les ensembles de niveaux d'une fonction diff??rentiable sur M (le terme technique de ??diffusion de hyperplan tangente non int??grable totalement"). Pr??s de chaque point p, une distribution de hyperplan est d??termin??e par une fuite nulle part 1-forme , Qui est unique ?? la multiplication par une fonction de fuite nulle part:

A 1-forme locale sur M est un formulaire de contact si la restriction de son d??riv??e ext??rieure ?? H est un non-d??g??n??r??e 2-forme et induit une structure symplectique sur H _p ?? chaque point ainsi. Si la distribution H peut ??tre d??finie par une 1-forme mondiale alors cette forme est le contact si et seulement si la forme sup??rieure dimensions

est un forme volume sur M, ce est ?? dire ne se annule pas ne importe o??. Un analogue du th??or??me de Darboux de contact d??tient: toutes les structures de contact sur un collecteur de dimension impaire sont localement isomorphes et peuvent ??tre amen??s ?? une certaine forme normale locale par un choix appropri?? du syst??me de coordonn??es.

Complexe et la g??om??trie K??hler

G??om??trie diff??rentielle complexe est l'??tude des vari??t??s complexes. Une vari??t?? presque complexe est un v??ritable collecteur , Dot??e d'une tenseur Type (1,1), soit une fibr?? endomorphisme (appel?? structure presque complexe)

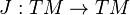, Tel que .

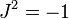Il d??coule de cette d??finition qu'un vari??t?? presque complexe est encore dimensions.

Une vari??t?? presque complexe est appel?? complexe si O?? 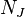est un tenseur de type (2,1) li??es ?? , Appel??e Nijenhuis tenseur (ou parfois de torsion). Une vari??t?? presque complexe est complexe si et seulement si il admet une holomorphe coordonner atlas. Une structure presque hermitienne est donn??e par une structure presque complexe J, avec une riemannian m??trique g, satisfaisant ?? la condition de compatibilit?? 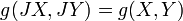. Une structure presque hermitienne d??finit naturellement 2-forme diff??rentielle . Les deux conditions suivantes sont ??quivalentes:

o?? est le Connexion de Levi-Civita de 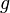. Dans ce cas, 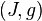est appel?? un La structure K??hler, et un collecteur K??hler est un collecteur dot?? d'une structure K??hler. En particulier, un collecteur est ?? la fois un K??hler complexe et un vari??t?? symplectique. Une grande classe de vari??t??s de K??hler (la classe de Collecteurs Hodge) est donn??e par tous les lisse vari??t??s projectives complexes.

La g??om??trie CR

G??om??trie CR est l'??tude de la g??om??trie intrins??que des limites des domaines dans vari??t??s complexes.

Ensembles et connexions

Appareil de fibr??s vectoriels, fibr??s principaux, et connexions sur eux joue un r??le extr??mement important dans la g??om??trie diff??rentielle moderne. Une vari??t?? lisse porte toujours un faisceau de vecteur naturel, le bundle tangente. Grosso modo, cette structure en elle-m??me ne est suffisante que pour le d??veloppement de l'analyse sur le collecteur, tout en faisant la g??om??trie n??cessite en plus un moyen de relier les espaces tangents ?? diff??rents points, ?? savoir la notion de transport parall??le. Un exemple important est fourni par connexions affines. Pour un R ³ en surface, plans tangents en diff??rents points peut ??tre identifi??e en utilisant le caract??re plat de l'espace euclidien ambiante. En La g??om??trie de Riemann, le Connexion de Levi-Civita sert un objectif semblable. Plus g??n??ralement, les g??om??tres diff??rentielles consid??rent espaces avec un faisceau de vecteur et une connexion en remplacement de la notion de Vari??t?? riemannienne. Dans cette approche, le faisceau est au collecteur externe et doit ??tre sp??cifi?? en tant que partie de la structure, tandis que la connexion fournit une am??lioration suppl??mentaire. En physique, le collecteur peut ??tre le espace-temps et faisceaux et les connexions correspondent ?? diff??rents domaines physiques.

Intrins??que par rapport extrins??que

Initialement et jusqu'au milieu du XIXe si??cle , la g??om??trie diff??rentielle a ??t?? ??tudi??e du point de vue extrins??que: courbes et les surfaces ont ??t?? consid??r??es comme se trouvant dans un espace euclidien de dimension plus ??lev??e (par exemple une surface en un l'espace de trois dimensions ambiante). Les r??sultats les plus simples sont ceux de la g??om??trie diff??rentielle des courbes. ?? commencer par les travaux de Riemann , le point de vue intrins??que a ??t?? d??velopp??, dans lequel on ne peut pas parler de d??placer ??en dehors?? de l'objet g??om??trique, car il est consid??r?? comme donn?? d'une mani??re autonome.

Le point de vue intrins??que est plus souple. Par exemple, il est utile dans la relativit?? o?? l'espace-temps ne peut naturellement ??tre pris comme extrins??que (ce qui serait ??l'ext??rieur?? il?). Avec le point de vue intrins??que, il est plus difficile ?? d??finir le concept central de courbure et d'autres structures telles que connexions, donc il ya un prix ?? payer.

Ces deux points de vue peuvent ??tre concili??s, ce est ?? dire la g??om??trie extrins??que peut ??tre consid??r?? comme une structure additionnelle ?? celle intrins??que. (Voir la Nash int??gration th??or??me.)

Applications de g??om??trie diff??rentielle

Voici quelques exemples de la fa??on dont la g??om??trie diff??rentielle est appliqu??e ?? d'autres domaines de la science et des math??matiques.

• Dans la physique , la g??om??trie diff??rentielle est la langue dans laquelle d'Einstein la th??orie de la relativit?? g??n??rale est exprim??e. Selon la th??orie, l'univers est une vari??t?? lisse ??quip?? pseudo-m??trique riemannienne, qui d??crit le courbure de l'espace-temps. La compr??hension de cette courbure est essentiel pour le positionnement de satellites en orbite autour de la terre. G??om??trie diff??rentielle est ??galement indispensable dans l'??tude des lentille gravitationnelle et les trous noirs .
• Dans l'??conomie , la g??om??trie diff??rentielle a des applications au domaine de la ??conom??trie.
• Mod??lisation g??om??trique (y compris infographie) et conception g??om??trique tirage assist??e par ordinateur sur les id??es de la g??om??trie diff??rentielle.
• Dans l'ing??nierie , la g??om??trie diff??rentielle peut ??tre appliqu?? pour r??soudre les probl??mes dans traitement num??rique du signal.
• Dans la physique , l'utilisation de formes diff??rentielles sont utiles dans l'??tude de l'??lectromagn??tisme .
• Dans la physique , la g??om??trie diff??rentielle a des applications ?? la fois ??quations de Lagrange et M??canique hamiltonienne. Vari??t??s symplectiques en particulier, peuvent ??tre utilis??es pour ??tudier Syst??mes hamiltoniens.