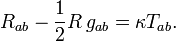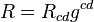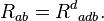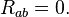La relativit?? g??n??rale
Renseignements g??n??raux
Cette s??lection Wikipedia est d??connect?? disponibles ?? partir enfants SOS pour la distribution dans le monde en d??veloppement. Une bonne fa??on d'aider d'autres enfants est de parrainer un enfant
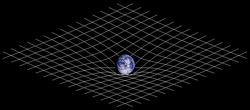
La relativit?? g??n??rale ou la th??orie de la relativit?? g??n??rale est le g??om??trique th??orie de la gravitation publi?? par Albert Einstein en 1916. Ce est la description l'??tat de l'art de la gravit?? dans moderne physique . Il unifie la relativit?? restreinte et La loi de Newton de la gravitation universelle, et d??crit la gravit?? comme une propri??t?? de la g??om??trie de l'espace et temps, ou l'espace-temps. En particulier, la courbure de l'espace-temps est directement li??e ?? la quatre impulsion ( masse-??nergie et lin??aire dynamique ) de tout ce qui importe et rayonnement sont pr??sents. La relation est d??finie par la Einstein Les ??quations de champ, un syst??me de ??quations aux d??riv??es partielles .
Les pr??dictions de la relativit?? g??n??rale diff??rent consid??rablement de celles de la physique classique, en particulier concernant le passage du temps, la g??om??trie de l'espace, le mouvement des corps dans chute libre, et la propagation de la lumi??re . Des exemples de telles diff??rences incluent gravitationnelle dilatation du temps, la redshift gravitationnel de la lumi??re, et de la gravitationnelle temporisation. Les pr??dictions de la relativit?? g??n??rale ont ??t?? confirm??s dans tous les observations et exp??riences ?? ce jour. Bien que la relativit?? g??n??rale est pas la seule th??orie relativiste de la gravit??, il est le plus simple telle th??orie qui est compatible avec les donn??es exp??rimentales. Toutefois, des questions restent sans r??ponse, ??tant le plus fondamental comment la relativit?? g??n??rale peut ??tre concili??e avec les lois de la physique quantique pour produire une th??orie compl??te et auto-coh??rent de la gravit?? quantique.
La th??orie d'Einstein a des applications astrophysiques importants. Il pointe vers l'existence de trous noirs -r??gions de l'espace o?? l'espace et le temps sont d??form??s de mani??re ?? ce que rien, pas m??me la lumi??re, ne peut ??chapper, comme un ??tat final pour les massives ??toiles . Il existe des preuves que cette trous noirs stellaires ainsi que plusieurs vari??t??s massives de trou noir sont responsables de l'intense rayonnement ??mis par certains types d'objets astronomiques tels que noyaux actifs de galaxies ou microquasars. La courbure de la lumi??re par gravit?? peut conduire au ph??nom??ne de lentille gravitationnelle, o?? plusieurs images du m??me objet astronomique ??loign??e sont visibles dans le ciel. La relativit?? g??n??rale pr??dit ??galement l'existence de ondes gravitationnelles, qui ont depuis ??t?? mesur??es indirectement; une mesure directe est le but de projets tels que LIGO. En outre, la relativit?? g??n??rale est ?? la base des actuelles cosmologiques mod??les d'un univers en expansion.
| La relativit?? g??n??rale |
|---|
 |
| Introduction Formulation math??matique Ressources |
Concepts fondamentaux |
Ph??nom??nes Probl??me de Kepler ?? Objectifs ?? Flots Cadre tra??ner ?? Effet g??od??sique Event horizon ?? Singularit?? Trou noir |
??quations Approximation des champs faibles Formalisme post-newtonien ??quation d'Einstein ??quation g??od??sique ??quations de Friedmann Formalisme ADM BSSN formalisme ??quation de Hamilton-Jacobi-Einstein |
Th??ories avanc??es Kaluza-Klein La gravit?? quantique |
Solutions Schwarzschild Reissner-Nordstr??m ?? G??del Kerr ?? Kerr-Newman Kasner ?? Taub-NUT ?? Milne ?? Robertson-Walker pp-ondes ?? la poussi??re van Stockum |
Les scientifiques Einstein ?? Lorentz ?? Hilbert ?? Poincar?? ?? Schwarzschild ?? ?? Sitter Reissner ?? Nordstr??m ?? Weyl ?? Eddington ?? Friedman ?? Milne ?? Zwicky ?? Lema??tre ?? G??del ?? Wheeler ?? Robertson ?? Bardeen ?? Walker ?? Kerr ?? Chandrasekhar ?? Ehlers ?? Penrose ?? Hawking ?? Taylor ?? Hulse ?? Stockum ?? Taub ?? Nouvel Homme Yau ?? Thorne autres |
Spacetime Spacetime Minkowski espace-temps diagrammes de Spacetime Spacetime en relativit?? g??n??rale |
Histoire
Peu de temps apr??s la publication de la th??orie de la relativit?? en 1905, Einstein commenc?? ?? penser ?? la fa??on d'int??grer gravit?? dans son nouveau cadre relativiste. En 1907, en commen??ant par un simple pensait exp??rience impliquant un observateur en chute libre, il se embarqua sur ce qui serait une recherche de huit ans pour une th??orie relativiste de la gravitation. Apr??s de nombreux d??tours et les faux d??parts, son travail a abouti ?? la Novembre, 1915 pr??sentation au Prussienne Acad??mie des Sciences de ce qui est maintenant connu sous le nom ??quation d'Einstein. Ces ??quations indiquent comment la g??om??trie de l'espace et le temps est influenc?? par tout ce qui importe est pr??sent, et forment le noyau de la th??orie g??n??rale de la relativit?? d'Einstein.
Les ??quations de champ d'Einstein sont non lin??aire et tr??s difficile ?? r??soudre. Einstein a utilis?? des m??thodes d'approximation dans l'??laboration de pr??visions initiales de la th??orie. Mais d??s 1916, l'astrophysicien Karl Schwarzschild trouv?? la premi??re solution exacte non n??gligeable aux ??quations de champ d'Einstein, le soi-disant M??trique de Schwarzschild. Cette solution a jet?? les bases pour la description des ??tapes finales de l'effondrement gravitationnel, et les objets connus aujourd'hui comme les trous noirs . Dans la m??me ann??e, les premiers pas vers la g??n??ralisation de la solution de Schwarzschild ?? ??lectriquement charg??es objets ont ??t?? prises, qui a finalement abouti ?? la Solution Reissner-Nordstr??m, maintenant associ?? avec des trous noirs charg??s. En 1917, Einstein a appliqu?? sa th??orie ?? l' univers dans son ensemble, initiant le domaine de relativiste la cosmologie . En ligne avec la pens??e contemporaine, il a assum?? un univers statique, l'ajout d'un nouveau param??tre ?? son domaine d'origine ??quations-le constante cosmologique ?? reproduire cette ??observation??. En 1929, cependant, le travail de Hubble et d'autres ont montr?? que notre univers est en expansion. Ce est facilement d??crite par les solutions cosmologiques expansion trouv??s par Friedmann en 1922, qui ne n??cessitent pas une constante cosmologique. Lema??tre a utilis?? ces solutions de formuler la premi??re version des big bang mod??les, dans laquelle notre univers a ??volu?? ?? partir d'un ??tat ant??rieur extr??mement chaud et dense. Einstein a d??clar?? plus tard la constante cosmologique la plus grande erreur de sa vie.
Pendant cette p??riode, la relativit?? g??n??rale est rest?? quelque chose d'une curiosit?? parmi les th??ories physiques. Ce est nettement sup??rieure ?? Gravitation newtonienne, ??tant compatible avec la relativit?? restreinte et de la comptabilit?? pour plusieurs effets inexpliqu??s par la th??orie newtonienne. Einstein lui-m??me avait montr?? en 1915 comment sa th??orie explique la anormale avance du p??rih??lie de la plan??te Mercure sans param??tres arbitraires (les ??facteurs de fudge??). De m??me, une exp??dition men??e par 1919 Eddington a confirm?? la pr??diction de la relativit?? g??n??rale pour la d??viation de la lumi??re des ??toiles par le Soleil, ce qui rend instantan??ment c??l??bre Einstein. Pourtant, la th??orie est entr?? dans le courant dominant de la la physique th??orique et l'astrophysique seulement avec les d??veloppements entre environ 1960 et 1975, maintenant connu sous le nom L'??ge d'or de la relativit?? g??n??rale. Les physiciens ont commenc?? ?? comprendre le concept d'un trou noir , et d'identifier la manifestation astrophysique de ces objets quasars. Des tests du syst??me solaire de plus en plus pr??cises ont confirm?? pouvoir pr??dictif de la th??orie, et la cosmologie relativiste, aussi, sont devenus pr??te ?? diriger des tests d'observation.
De la m??canique classique ?? la relativit?? g??n??rale
La relativit?? g??n??rale est mieux comprise en examinant ses similitudes avec les d??parts ?? partir de la physique classique. La premi??re ??tape est la r??alisation que la m??canique classique et la loi de la gravitation de Newton admettent une description g??om??trique. La combinaison de cette description avec les lois de r??sultats de la relativit?? restreinte dans une d??rivation heuristique de la relativit?? g??n??rale.
G??om??trie de la gravitation newtonienne
A la base de la m??canique classique est la notion qu'un La motion de corps peut ??tre d??crit comme une combinaison de libre (ou inertiel) mouvement, et les ??carts de ce mouvement libre. Ces ??carts sont caus??es par des forces externes agissant sur un corps, selon la deuxi??me de Newton loi du mouvement , qui stipule que la vigueur agissant sur un corps est ??gale ?? (inertie) de ce corps la masse fois son acc??l??ration . Les mouvements inertiels pr??f??r??s sont li??s ?? la g??om??trie de l'espace et le temps : dans la norme cadres de r??f??rence de la m??canique classique, les objets en mouvement libre se d??placent le long des lignes droites ?? vitesse constante. En langage moderne, leurs chemins sont g??od??siques, droite lignes de monde dans l'espace-temps.
Inversement, on pourrait se attendre ?? ce que les mouvements inertiels, une fois identifi??s par l'observation des mouvements r??els des organes et de faire des provisions pour les forces externes (comme l'??lectromagn??tisme ou frottement), peut ??tre utilis?? pour d??finir la g??om??trie de l'espace, ainsi que d'un temps coordonner. Cependant, il ya une ambigu??t??, une fois la gravit?? entre en jeu. Selon La loi de Newton de gravit??, et v??rifi??e de fa??on ind??pendante par des exp??riences telles que celle de E??tv??s et ses successeurs (voir E??tv??s exp??rience), il existe un universalit?? de la chute libre (??galement connu sous le nom faible principe d'??quivalence, ou l'??galit?? universelle de masse inertielle et gravitationnelle passive): la trajectoire d'un corps d'??preuve en chute libre ne d??pend que de sa position et de la vitesse initiale, mais pas sur l'une de ses propri??t??s de mat??riau. Une version simplifi??e de ce est incarn?? dans l'exp??rience de l'ascenseur d'Einstein, illustr?? dans la figure sur la droite: pour un observateur dans une petite pi??ce ferm??e, il est impossible de d??cider, en cartographiant la trajectoire des corps comme une balle ?? terre, si la chambre est au repos dans un champ gravitationnel, ou dans l'espace libre bord d'une fus??e acc??l??r??.
Compte tenu de l'universalit?? de la chute libre, il n'y a pas de distinction entre le mouvement observable inertielle et le mouvement sous l'influence de la force gravitationnelle. Cela sugg??re la d??finition d'une nouvelle classe de mouvement inertiel, ?? savoir que des objets en chute libre sous l'influence de la gravit??. Cette nouvelle classe de mouvements pr??f??r??s, aussi, d??finit une g??om??trie de l'espace et du temps en termes math??matiques, ce est le mouvement g??od??sique associ?? ?? un particulier liaison qui d??pend de la du gradient potentiel gravitationnel. Espace, dans cette construction, a encore l'ordinaire la g??om??trie euclidienne . Cependant, l'espace-temps dans son ensemble est plus complexe. Comme on peut ??tre montr?? en utilisant de simples pens?? exp??riences suivantes les trajectoires de chute libre de particules de test diff??rentes, le r??sultat de transporter des vecteurs de l'espace-temps qui peut d??noter la vitesse d'une particule (vecteurs de genre temps) varie avec la trajectoire de la particule; math??matiquement parlant, la connexion ne est pas newtonien int??grable. De cela, on peut en d??duire que l'espace-temps est courbe . Le r??sultat est une formulation g??om??trique de gravit?? de Newton en utilisant uniquement covariantes concepts, ce est ?? dire une description qui est valable dans tous les syst??me de coordonn??es souhait??. Dans cette description g??om??trique, les effets de la mar??e acc??l??ration relative des corps en chute libre-sont li??s ?? la d??riv??e de la connexion, en montrant comment la g??om??trie modifi??e est caus??e par la pr??sence de la masse.
G??n??ralisation relativiste
Aussi fascinante que la gravit?? newtonienne g??om??trique peut ??tre, son fondement, la m??canique classique, est simplement un cas limite d' relativistes (sp??ciales) de la m??canique. Dans le langage de la sym??trie : o?? la gravit?? peut ??tre n??glig??e, la physique est Lorentz invariant comme dans la relativit?? restreinte plut??t que Galilei invariant comme dans la m??canique classique. (La sym??trie d??finition de la relativit?? restreinte est la Groupe de Poincar?? qui comprend ??galement les traductions et les rotations.) Les diff??rences entre les deux deviennent significatives lorsque nous traitons avec des vitesses approchant de la vitesse de la lumi??re , et ?? des ph??nom??nes de haute ??nergie.
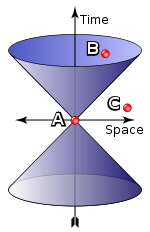
Avec la sym??trie de Lorentz, structures suppl??mentaires entre en jeu. Ils sont d??finis par l'ensemble des c??nes de lumi??re (voir l'image sur la gauche). Les l??gers c??nes d??finissent une structure causale: pour chaque ??v??nement A, il ya un ensemble d'??v??nements qui peut, en principe, que ce soit influencer ou ??tre influenc?? par un par des signaux ou des interactions qui ne ont pas besoin de voyager plus vite que la lumi??re (comme ??v??nement B dans l'image), et un ensemble d'??v??nements pour lesquels une telle influence est impossible (comme ??v??nement C dans l'image). Ces ensembles sont observateur ind??pendant. En conjonction avec les lignes d'univers de particules en chute libre, la lumi??re-c??nes peuvent ??tre utilis??s pour reconstruire m??trique semi-riemannienne de l'espace-temps, au moins jusqu'?? un facteur scalaire positif. En termes math??matiques, cela d??finit un la structure conformationnelle.
Relativit?? sp??cial est d??fini en l'absence de gravit??, de sorte que pour des applications pratiques, ce est un mod??le appropri?? chaque fois que la gravit?? peut ??tre n??glig??e. Apporter gravit?? en jeu, et en supposant que l'universalit?? de la chute libre, un raisonnement analogue que dans la section pr??c??dente se applique: il n'y a pas mondiale r??f??rentiels inertiels. Au lieu de cela il ya les r??f??rentiels inertiels approximatives mobiles particules aux c??t??s de chute libre. Traduit dans le langage de l'espace-temps: la derni??re ligne droite les d??lais analogue qui d??finissent un rep??re inertiel sans gravit?? sont d??form??es ?? des lignes qui sont courb??es par rapport ?? l'autre, ce qui sugg??re que l'inclusion de gravit?? n??cessite une modification de la g??om??trie de l'espace-temps.
A priori, il ne est pas clair si les nouveaux cadres locaux en chute libre co??ncider avec les cadres de r??f??rence dans lequel les lois de la relativit?? restreinte retenue que la th??orie est bas??e sur la propagation de la lumi??re, et donc sur l'??lectromagn??tisme , ce qui pourrait avoir un ensemble diff??rent de trames pr??f??r??. Mais en utilisant diff??rentes hypoth??ses sur les cadres sp??ciaux relativiste (comme leur ??tant terre fixe, ou en chute libre), on peut d??duire des pr??dictions diff??rentes pour le d??calage vers le rouge de gravitation, ce est la mani??re dont la fr??quence des d??placements lumineux que la lumi??re se propage ?? travers un champ de gravitation (cf. ci-dessous ). Les mesures r??elles montrent que les cadres en chute libre sont ceux dans lesquels la lumi??re se propage comme il le fait dans la relativit?? sp??ciale. La g??n??ralisation de cette d??claration, ?? savoir que les lois de la relativit?? attente particuli??re ?? bonne approximation en chute libre (et non-rotation) des cadres de r??f??rence, est connu comme le Einstein principe d'??quivalence, un principe directeur essentiel pour g??n??raliser la physique relativiste sp??ciales pour inclure gravit??.
Les m??mes donn??es exp??rimentale montre que le temps tel que mesur?? par des horloges dans un gravitationnelle de terrain bon moment, pour donner le mandat de suivi technique ne pas les r??gles de la relativit?? restreinte. Dans le langage de la g??om??trie de l'espace-temps, il ne est pas mesur??e par le M??trique de Minkowski. Comme dans le cas newtonien, ce est ??vocateur d'une g??om??trie plus g??n??rale. ?? petite ??chelle, tous les cadres de r??f??rence qui sont en chute libre sont ??quivalentes, et d'environ Minkowski. Par cons??quent, nous traitons maintenant avec une g??n??ralisation courbe l'espace de Minkowski. Le tenseur m??trique qui d??finit la g??om??trie en particulier, comment longueurs et les angles sont mesur??s-ne est pas la m??trique de Minkowski de la relativit?? restreinte, ce est une g??n??ralisation connu comme un semi ou pseudo-m??trique riemannienne. En outre, chaque m??trique riemannienne est naturellement associ??e ?? un type particulier de connexion, le Connexion de Levi-Civita, et ce est, en fait, la connexion qui satisfait le principe d'??quivalence et rend espace localement minkowskien (ce est, en coordonn??es appropri??es "localement inertiels", la m??trique est Minkowski, et ses d??riv??s et les coefficients de connexion disparaissent) .
Les ??quations d'Einstein
Ayant formul?? relativiste, la version g??om??trique des effets de la gravit??, la question de la source de gravit?? reste. Dans la gravitation newtonienne, la source est la masse. Dans la relativit?? restreinte, la masse se av??re ??tre une partie d'une quantit?? plus g??n??ral appel?? tenseur impulsion-??nergie, qui comprend ?? la fois l'??nergie et l'??lan densit??s ainsi que le stress (ce est- pression et cisaillement). En utilisant le principe d'??quivalence, ce tenseur est facilement g??n??ralisable ?? espace-temps courbe. Dessin en outre sur l'analogie avec la gravit?? newtonienne g??om??trique, il est naturel de supposer que le ??quation de champ de la gravit?? concerne ce tenseur et de la Tenseur de Ricci, qui d??crit une classe particuli??re d'effets de mar??e: le changement de volume pour un petit nuage de particules de test qui sont initialement au repos, puis tombent librement. Dans la relativit?? restreinte, conservation de l'??nergie-impulsion correspond ?? la d??claration que le tenseur impulsion-??nergie est de divergence nulle. Cette formule, aussi, est facilement g??n??ralisable ?? l'espace-temps courb?? par le remplacement d??riv??es partielles avec leurs homologues courbes-collecteur, d??riv??es covariantes. Avec cette condition-la divergence covariante suppl??mentaire du tenseur impulsion-??nergie, et donc de tout ce qui est de l'autre c??t?? de l'??quation, est z??ro l'ensemble simple d'??quations sont ce qu'on appelle (le terrain) des ??quations d'Einstein:
Sur le c??t?? gauche est une combinaison sp??cifique de divergence nulle de la Tenseur de Ricci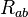 
et la m??trique connu sous le nom Tenseur d'Einstein. En particulier,
est le scalaire de courbure. Le tenseur de Ricci lui-m??me est li??e ?? la plus g??n??rale tenseur de courbure de Riemann que
Sur le c??t?? droit, T ab est le tenseur impulsion-??nergie. Tous les tenseurs sont ??crits en notation d'index abstrait. Correspondant ?? la pr??diction de la th??orie aux r??sultats d'observation pour la plan??te orbites (ou, de fa??on ??quivalente, assurant que le faible gravit??, limite basse vitesse est la m??canique newtonienne), la constante de proportionnalit?? peuvent ??tre fix??s comme κ = 8π G / c 4, avec le G constante gravitationnelle et c la vitesse de la lumi??re . Lorsqu'il n'y a pas mati??re pr??sente, de sorte que le tenseur impulsion-??nergie dispara??t, le r??sultat est le vide ??quations d'Einstein,
Il y a alternatives ?? la relativit?? g??n??rale construite sur les m??mes locaux, qui comprennent les r??gles et / ou des contraintes suppl??mentaires, conduisant ?? diff??rentes ??quations de champ. Des exemples sont Brans-Dicke th??orie, teleparallelism, et Th??orie d'Einstein-Cartan.
D??finition et applications de base
La d??rivation d??crit dans la section pr??c??dente contient toutes les informations n??cessaires pour d??finir la relativit?? g??n??rale, d??crire ses propri??t??s cl??s et r??pondre ?? une question d'une importance cruciale dans la physique, ?? savoir comment la th??orie peut ??tre utilis?? pour la construction de mod??les.
D??finition et propri??t??s de base
La relativit?? g??n??rale est une la th??orie m??trique de la gravitation . En son centre se Les ??quations d'Einstein, qui d??crivent la relation entre la g??om??trie d'un ?? quatre dimensions, semi- Riemann collecteur repr??sentant l'espace temps d'une part, et la ??nergie impulsion contenue dans l'espace-temps que de l'autre. Ph??nom??nes qui en m??canique classique sont attribu??s ?? l'action de la force de gravit?? (comme chute libre, mouvement orbital, et vaisseau spatial trajectoires), correspondent au mouvement inertiel dans un g??om??trie courbe l'espace-temps en relativit?? g??n??rale; il ne est pas force gravitationnelle d??vier les objets de leurs chemins, droites naturelles. Au lieu de cela, la gravit?? correspond ?? des changements dans les propri??t??s de l'espace et le temps, qui ?? son tour modifie les chemins les plus droites possible que les objets-suivra naturellement. La courbure est, ?? son tour, provoqu?? par l'??nergie-impulsion de la mati??re. Paraphrasant le relativiste John Archibald Wheeler, l'espace-temps dit importe comment se d??placer; question raconte comment l'espace-temps courbe.
Alors que la relativit?? g??n??rale remplace le scalaire potentiel gravitationnel de la physique classique par un sym??trique rang deux tenseur, ce dernier se r??duit ?? l'ancienne dans certains cas limites. Pour faibles champs gravitationnels et vitesse lente par rapport ?? la vitesse de la lumi??re, les pr??dictions de la th??orie convergent sur ceux de La loi de la gravitation de Newton.
Comme il est construit ?? partir tenseurs, des expositions de la relativit?? g??n??rale covariance g??n??rale: ses lois et d'autres lois-formul??s dans le cadre relativiste g??n??rale-prise sur la m??me forme dans tous les les syst??mes de coordonn??es. En outre, la th??orie ne contient pas de structures de base g??om??triques invariantes. Il a ainsi satisfait une plus stricte principe de la relativit?? g??n??rale, ?? savoir que le les lois de la physique sont les m??mes pour tous les observateurs. Localement, exprim??e dans la principe d'??quivalence, l'espace-temps est Minkowski, et les lois de la physique exposition invariance de Lorentz locale.
Construction de mod??les
Le concept de base de la construction du mod??le g??n??ral-relativiste est celle d'un solution des ??quations d'Einstein. ??tant donn?? les deux ??quations d'Einstein et les ??quations appropri??es pour les propri??t??s de la mati??re, une telle solution se compose d'un collecteur sp??cifique semi-riemannienne (g??n??ralement d??finie en donnant la m??trique en coordonn??es sp??cifiques), et champs de mati??re sp??cifiques d??finis sur ce collecteur. Mati??re et la g??om??trie doivent satisfaire les ??quations d'Einstein, donc en particulier, ??nergie-impulsion tenseur de la question doivent ??tre libres divergence. La question doit, bien s??r, satisfaire ??galement wheatever ??quations suppl??mentaires ont ??t?? impos??es sur ses propri??t??s. En bref, une telle solution est un mod??le de l'univers qui satisfait les lois de la relativit?? g??n??rale, et les lois ??ventuellement suppl??mentaires r??gissant toute affaire pourrait ??tre pr??sente.
Les ??quations d'Einstein sont non lin??aires ??quations aux d??riv??es partielles et, en tant que tels, difficiles ?? r??soudre exactement. N??anmoins, un certain nombre de solutions exactes sont connues, bien que seulement quelques-uns ont des applications physiques directes. Les solutions exactes les plus connus, et aussi les plus int??ressants d'un point de vue physique, sont les Solution de Schwarzschild, le Solution Reissner-Nordstr??m et M??trique de Kerr, correspondant chacun ?? un certain type de trou noir dans un univers par ailleurs vide, et Friedmann-Lema??tre-Robertson-Walker et univers de Sitter, d??crivant chaque un cosmos en expansion. Solutions exactes de grand int??r??t th??orique comprennent la G??del univers (qui ouvre la possibilit?? fascinante de Voyage dans le temps dans des espaces-temps courbes), le Solution Taub-NUT (un univers de mod??le qui est homog??ne, mais anisotrope), et Espace anti-de Sitter (qui a r??cemment pris de l'importance dans le contexte de ce qu'on appelle la Maldacena conjecture).
Compte tenu de la difficult?? de trouver des solutions exactes, les ??quations de champ d'Einstein sont ??galement r??solus souvent par int??gration num??rique sur un ordinateur, ou en consid??rant petites perturbations de solutions exactes. Dans le domaine de relativit?? num??rique, ordinateurs puissants sont employ??s pour simuler la g??om??trie de l'espace-temps et de r??soudre les ??quations d'Einstein pour les situations int??ressantes comme collision de deux trous noirs . En principe, ces m??thodes peuvent ??tre appliqu??es ?? ne importe quel syst??me, ??tant donn?? les ressources informatiques suffisantes, et peuvent r??pondre ?? des questions fondamentales telles que singularit??s nues. Solutions approximatives peuvent ??galement ??tre trouv??s par th??ories de perturbation tels que lin??aris?? gravit?? et sa g??n??ralisation, le l'expansion post-newtonien, qui tous deux ont ??t?? mis au point par Einstein. Ce dernier fournit une approche syst??matique ?? la r??solution de la g??om??trie de l'espace-temps qui contient une distribution de la mati??re qui se d??place lentement par rapport ?? la vitesse de la lumi??re. L'expansion implique une s??rie de termes; les premiers termes repr??sentent la gravitation newtonienne, alors que les termes ult??rieures repr??sentent toujours plus petites corrections ?? la th??orie de Newton en raison de la relativit?? g??n??rale. Une extension de cette expansion est le post-newtonienne (PPN) param??tr??e, ce qui permet des comparaisons quantitatives entre les pr??dictions de la relativit?? g??n??rale et th??ories alternatives.
Cons??quences de la th??orie d'Einstein
La relativit?? g??n??rale a un certain nombre de cons??quences physiques. Certains suivent directement ?? partir des axiomes de la th??orie, alors que d'autres sont devenus clairement qu'au cours des 90 ann??es de recherche qui ont suivi la premi??re publication d'Einstein.
Gravitationnelle dilatation du temps et de d??placement de fr??quence
En supposant que le principe d'??quivalence tient, la gravit?? influence le passage du temps. Lumi??re fait descendre dans un puits de gravit?? est d??cal??es vers le bleu, tandis que la lumi??re envoy??e dans la direction oppos??e (?? savoir, l'escalade de la gravit?? ainsi) est d??cal??e vers le rouge ; Collectivement, ces deux effets sont connus comme le d??calage de fr??quence de la gravit??. Plus g??n??ralement, traite pr??s d'une piste de corps massif plus lentement par rapport aux processus qui se d??roulent plus loin; cet effet est connu sous le nom de gravitation dilatation du temps.
Redshift gravitationnel a ??t?? mesur??e en laboratoire et ?? partir d'observations astronomiques. Gravitationnelle dilatation du temps dans le champ gravitationnel de la Terre a ??t?? mesur??e ?? plusieurs reprises ?? l'aide horloges atomiques, tandis que la validation en cours est fourni comme un effet secondaire de l'op??ration de la Syst??me de positionnement global (GPS). Tests dans les champs gravitationnels forts sont fournies par l'observation de pulsars binaires. Tous les r??sultats sont en accord avec la relativit?? g??n??rale. Cependant, au niveau actuel de pr??cision, ces observations ne peuvent pas distinguer entre la relativit?? g??n??rale et d'autres th??ories dans lesquelles le principe d'??quivalence est valable.
D??viation de la lumi??re et de retard de temps gravitationnelle
Relativit?? g??n??rale pr??voit que la trajectoire de la lumi??re est courb?? dans un champ de gravitation; le passage d'un corps massif lumi??re est d??vi??e vers ce corps. Cet effet a ??t?? confirm?? par l'observation de la lumi??re des ??toiles ou ??loign??es quasars ??tant d??vi??s car il passe le Soleil .
Ce et les pr??visions connexes suivre du fait que la lumi??re suit ce qu'on appelle une lumi??re semblable ou null g??od??sique-une g??n??ralisation des lignes droites le long de laquelle la lumi??re se propage dans la physique classique. Ces g??od??siques sont la g??n??ralisation de la invariance de LightSpeed dans la relativit?? restreinte . Comme on examine spacetimes mod??les appropri??s (soit l'ext??rieur Solution de Schwarzschild ou, pour plus d'une seule masse, le l'expansion post-newtonienne), plusieurs effets de la gravit?? sur la propagation de lumi??re ??mergent. Bien que la courbure de la lumi??re peut ??galement ??tre obtenue par l'extension de la universalit?? de la chute libre de la lumi??re , l'angle de braquage r??sultant de ces calculs ne est que la moiti?? de la valeur donn??e par la relativit?? g??n??rale.
??troitement li??e ?? d??viation de la lumi??re est le retard gravitationnelle de temps (ou l'effet Shapiro), le ph??nom??ne que les signaux de lumi??re prennent plus de temps pour se d??placer dans un champ gravitationnel qu'ils ne le feraient en l'absence de ce champ. Il ya eu de nombreux essais r??ussis de cette pr??diction. Dans le Th??orie PPN (PPN), des mesures ?? la fois de la d??viation de la lumi??re et le temps de retard de gravitation d??terminer un param??tre appel??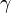 
Qui code pour l'influence de la gravit?? sur la g??om??trie de l'espace.
Les ondes gravitationnelles
Une de plusieurs analogies entre la gravit?? de champ faible et l'??lectromagn??tisme est que, analogue ?? ondes ??lectromagn??tiques , il ya ondes gravitationnelles: des ondulations dans la m??trique de l'espace-temps qui se propagent ?? la vitesse de la lumi??re . Le type le plus simple d'une telle onde peut ??tre visualis?? par son action sur un anneau de particules flottant librement (image du haut vers la droite). Une onde sinuso??dale se propageant ?? travers un tel anneau vers le lecteur d??forme la bague dans un mode rythmique caract??ristique (en bas, ?? l'image anim??e ?? droite). Depuis les ??quations d'Einstein sont non lin??aire, arbitrairement fortes ondes gravitationnelles ne ob??issent pas superposition lin??aire, ce qui rend difficile leur description. Cependant, pour des champs faibles, une approximation lin??aire peut ??tre effectu??e. Ces ondes gravitationnelles lin??aris??es sont suffisamment pr??cis pour d??crire les vagues extr??mement faibles qui devraient arriver sur Terre ?? partir de lointains ??v??nements cosmiques, qui se traduisent g??n??ralement dans distances relatives croissante et d??croissante par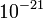 
ou moins. Les m??thodes d'analyse de donn??es font couramment usage du fait que ces ondes peuvent ??tre lin??aris??s D??compos?? Fourier.
Certains solutions exactes d??crivent ondes gravitationnelles sans aucune approximation, par exemple, un train d'ondes voyager dans l'espace vide ou soi-disant Univers Gowdy, vari??t??s de un cosmos en expansion remplis d'ondes gravitationnelles. Mais pour les ondes gravitationnelles produites dans des situations astrophysique pertinentes, telles que la fusion de deux trous noirs, les m??thodes num??riques sont actuellement le seul moyen pour construire des mod??les appropri??s.
Effets orbitaux et la relativit?? de la direction
La relativit?? g??n??rale diff??re de la m??canique classique dans un certain nombre de pr??dictions concernant corps en orbite. Il pr??dit une rotation d'ensemble ( pr??cession) des orbites plan??taires, ainsi que la pourriture orbitale caus?? par l'??mission d'ondes gravitationnelles et les effets li??s ?? la relativit?? de la direction.
Pr??cession des absides
Dans la relativit?? g??n??rale, le apsides de toute orbite (le point d'approche le plus proche du corps en orbite pour le syst??me de centre de masse ) sera -pr??cession de l'orbite ne est pas une ellipse , mais semblable ?? une ellipse qui tourne autour de son foyer, d'o?? une rose forme de la courbe comme (voir image). Einstein abord d??riv?? ce r??sultat en utilisant une m??trique approximative repr??sentant la limite newtonienne et traiter le corps comme une orbite particules de test. Pour lui, le fait que sa th??orie a donn?? une explication simple de la anormale passage au p??rih??lie de la plan??te Mercure , d??couvert plus t??t par Urbain Le Verrier en 1859, ??tait une preuve importante qu'il avait enfin identifi?? la forme correcte de la ??quations de la gravitation sur le terrain.
L'effet peut ??galement ??tre obtenu en utilisant soit l'exacte M??trique de Schwarzschild (d??crivant l'espace-temps autour d'une masse sph??rique) ou beaucoup plus g??n??rale formalisme post-newtonien. Elle est due ?? l'influence de la gravit?? sur la g??om??trie de l'espace et ?? la contribution de self-??nergie ?? la gravit?? d'un corps (cod?? dans le non-lin??arit?? des ??quations d'Einstein). Pr??cession relativiste a ??t?? observ??e pour toutes les plan??tes qui permettent pour des mesures pr??cises de pr??cession (Mercure, V??nus et de la Terre ), ainsi que dans syst??mes de Pulsar binaire, o?? il est plus grand par cinq ordres de grandeur.
D??croissance de l'orbite
Selon la relativit?? g??n??rale, une syst??me binaire ??mettra ondes gravitationnelles, perdant ainsi l'??nergie . En raison de cette perte, la distance entre les deux corps en orbite diminue, et il en va de leur p??riode orbitale. Dans le syst??me solaire ou ordinaire ??toiles doubles, l'effet est trop faible pour ??tre observable. Pas si d'un proche pulsar binaire, un syst??me de deux orbitant les ??toiles ?? neutrons, dont l'un est un pulsar: du pulsar, observateurs sur Terre re??oivent une s??rie r??guli??re d'impulsions radio qui peuvent servir comme une horloge de haute pr??cision, qui permet des mesures pr??cises de la p??riode orbitale. Depuis les ??toiles ?? neutrons sont tr??s compacts, d'importantes quantit??s d'??nergie sont ??mis sous la forme de rayonnement gravitationnel.
La premi??re observation d'une diminution de la p??riode orbitale due ?? l'??mission des ondes gravitationnelles a ??t?? faite par Hulse et Taylor, en utilisant le pulsar binaire PSR1913 + 16 qu'ils avaient d??couvert en 1974. Ce ??tait la premi??re d??tection des ondes gravitationnelles, quoique indirecte, pour lesquels ils ont re??u le 1993 Prix Nobel de physique. Depuis lors, plusieurs autres pulsars binaires ont ??t?? trouv??es, en particulier le pulsar double PSR J0737-3039, dans lequel les deux ??toiles sont pulsars.
Pr??cession g??od??sique et le cadre de tra??ner
Plusieurs effets relativistes sont directement li??s ?? la relativit?? de la direction. Un est pr??cession g??od??sique: la direction de l'axe d'un gyroscope en chute libre dans l'espace-temps courbe va changer par rapport, par exemple, avec la direction de la lumi??re re??ue de lointaines ??toiles, m??me si un tel gyroscope repr??sente la fa??on de garder une direction aussi stable que possible (" transport parall??le ") Pour la. Lune - Terre -syst??me, cet effet a ??t?? mesur??e ?? l'aide de laser lunaire allant. Plus r??cemment, il a ??t?? mesur?? pour les masses d'??preuve ?? bord du satellite Gravity Probe B avec une pr??cision meilleure que 1 pour cent.
Pr??s d'une masse en rotation, il ya ce qu'on appelle gravitomagnetic ou frame-glisser des effets. Un observateur distant d??terminera que les objets ?? proximit?? de la masse GET "tra??n?? autour". Ce est la plus extr??me pour trous noirs en rotation o??, pour tout objet entrant dans une zone connue comme la ergosph??re, la rotation est in??vitable. De tels effets peuvent ??tre test??s de nouveau par leur influence sur l'orientation des gyrom??tres en chute libre. Essais peu controvers??es ont ??t?? effectu??es en utilisant le LAGEOS satellites, confirmant la pr??diction relativiste. Une mesure de pr??cision est le but principal de la Mission Gravity Probe B, avec les r??sultats attendus en Septembre 2008.
Applications astrophysiques
Lentille gravitationnelle
La d??viation de la lumi??re par gravit?? est responsable d'une nouvelle classe de ph??nom??nes astronomiques. Si un objet massif est situ?? entre l'astronome et un objet cible distante avec masse et relatives des distances appropri??es, l'astronome verra plusieurs images d??form??es de la cible. De tels effets sont connus comme lentille gravitationnelle. Selon la configuration, l'??chelle, la distribution et de masse, il peut y avoir deux ou plusieurs images, un anneau brillant connu comme un Anneau d'Einstein, ou anneaux partiels appel??s arcs. Le premier exemple a ??t?? d??couvert en 1979; Depuis, plus d'une centaine de lentilles gravitationnelles ont été observés. Même si les multiples images sont trop proches les uns des autres pour être résolus, l'effet peut encore être mesurée, par exemple, comme un éclaircissement global de l'objet cible; un certain nombre de ces « événements de microlentille "a été observé.
Lentille gravitationnelle a développé un outil d' astronomie observationnelle. Il est utilisé pour détecter la présence et la distribution de la matière noire , fournir un "télescope naturel» pour l'observation de galaxies lointaines, et pour obtenir une estimation indépendante de la constante de Hubble . Évaluations statistiques des données de lentille fournissent de précieuses informations sur l'évolution structurelle de galaxies .
L'astronomie des ondes gravitationnelles
Observations des pulsars binaires fournissent des preuves solides indirecte de l'existence des ondes gravitationnelles (voir Décroissance de l'orbite , ci-dessus). Cependant, les ondes gravitationnelles qui nous parviennent des profondeurs du cosmos ont pas été détectée directement, ce qui est un objectif majeur de la recherche sur la relativité de courant. Plusieurs terrestres détecteurs d'ondes gravitationnelles sont actuellement en exploitation, notamment les détecteurs interférométriques GEO 600, LIGO (trois détecteurs), TAMA 300 et VIRGO. Un détecteur spatial américano-européen commun, LISA, est actuellement en cours de développement, avec une mission de précurseur ( LISA Pathfinder) lancement est prévu pour la fin de 2009.
Observations d'ondes gravitationnelles promettent de compléter les observations dans le spectre ??lectromagn??tique.Ils sont censés fournir des informations sur les trous noirs et autres objets denses tels que les étoiles à neutrons et les naines blanches, sur certains types desupernovaeimplosions, et sur ??????les processus dans l'univers très tôt, y compris la signature de certains types de hypothétiquecorde cosmique.
Les trous noirs et autres objets compacts
Chaque fois qu'un objet devient suffisamment compact, la relativité générale prédit la formation d'un trou noir , une région de l'espace à partir duquel rien, pas même la lumière, ne peut échapper. Dans les modèles actuellement reconnus de l'évolution stellaire, les étoiles à neutrons avec environ 1,4 masse solaire et dits trous noirs stellaires avec quelques-uns à quelques dizaines de masses solaires sont pensés pour être l'état final de l'évolution des étoiles massives. trous noirs supermassifs avec quelques millions à quelques milliards de masses solaires sont considérés comme la règle plutôt que l'exception dans les centres des galaxies, et leur présence est pensé pour avoir joué un rôle important dans la formation des galaxies et des grandes structures cosmiques.
Astronomiquement, la propriété la plus importante d'objets compacts est qu'ils fournissent un mécanisme superbement efficace pour convertir l'énergie gravitationnelle en rayonnement électromagnétique. désactualisation, la chute de poussière ou de corps gazeux sur stellaires ou des trous noirs supermassifs, est pensé pour être responsable de certains spectaculairement lumineuse objets astronomiques, notamment divers types de noyaux actifs de galaxies sur des échelles galactiques et objets stellaires de taille tels que microquasars. En particulier, l'accrétion peuvent conduire à des jets relativistes, axé faisceaux de particules hautement énergétiques qui sont jetés dans l'espace à près de vitesse de la lumière . La relativité générale joue un rôle central dans la modélisation de tous ces phénomènes, et les observations fournissent des preuves solides de l'existence des trous noirs avec les propriétés prédites par la théorie.
Les trous noirs sont également prisés des cibles dans la recherche d'ondes gravitationnelles (cf. ondes gravitationnelles , ci-dessus). Fusion binaires de trous noirs devraient conduire à certains des plus forts signaux d'ondes gravitationnelles atteignant détecteurs ici sur Terre, et la phase immédiatement avant la fusion («bip») pourraient être utilisés comme une " bougie standard "pour en déduire la distance à la Événements- de fusion et donc servir de sonde de l'expansion cosmique à de grandes distances. Les ondes gravitationnelles produites comme un stellaires plonge trou noir supermassif en un devraient fournir des informations directes sur la géométrie de Supermassive Black Hole.
Cosmologie
Les modèles actuels de la cosmologie sont basés sur les équations d'Einstein y compris?? constante cosmologique, ce qui a une influence importante sur la dynamique à grande échelle du cosmos,
où g ab est l' espace-temps métrique. isotrope et des solutions homogènes de ces équations améliorées, les solutions Friedmann-Lemaître-Robertson-Walker, permettra aux physiciens pour modéliser un univers qui a évolué au cours des 14 derniers milliards d'années à partir d'un, début chaud Big Bang phase. Une fois un petit nombre de paramètres (par exemple moyenne de l'univers question densité ) ont été fixés par l'observation astronomique, de nouvelles données d'observation peuvent être utilisés pour mettre les modèles à l'épreuve. Prédictions, tous les succès, notamment l'abondance initiale des éléments chimiques formés dans une période de nucléosynthèse primordiale, la structure à grande échelle de l'univers, et l'existence et les propriétés d'un " écho thermique »depuis le début des cosmos, la rayonnement de fond cosmologique.
Les observations astronomiques du taux d'expansion cosmologique permettent la quantité totale de matière dans l'univers à estimer, bien que la nature de cette question reste en partie mystérieuse. Environ 90 pour cent de toute la matière semble être dite matière noire , qui a une masse (ou, de façon équivalente, influence gravitationnelle), mais n'a pas d'interaction électromagnétique et, par conséquent, ne peut pas être observé directement. Il est généralement accepté description de ce nouveau type de matière, dans le cadre de connue physique des particules ou autrement. Les données d'observation à partir d'enquêtes de redshift de lointain supernovae et les mesures du rayonnement de fond cosmique montrent également que l'évolution de notre univers est fortement influencée par une constante cosmologique entraînant une accélération de l'expansion cosmique ou, de façon équivalente, par une forme d'énergie avec une inhabituelle équation de l'Etat, connu comme l'énergie sombre, dont la nature reste obscure.
Un soi-disant la phase inflationniste , une phase supplémentaire de l'expansion fortement accélérée à des moments cosmiques de l'ordre de 
secondes, a émis l'hypothèse en 1980 pour tenir compte de plusieurs observations énigmatiques qui ont été inexpliquée par les modèles cosmologiques classiques, tels que l'homogénéité presque parfaite du rayonnement de fond cosmique . Des mesures récentes du rayonnement de fond cosmique ont abouti à la première preuve de ce scénario. Cependant, il existe une multitude de possibles scénarios inflationnistes, qui ne peut être pas restreint par les observations actuelles. Une question encore plus grande est la physique de l'univers plus tôt, avant la phase inflationniste et à proximité de l'endroit où les modèles classiques prédisent le big bang singularité. Une réponse autorité nécessiterait une théorie complète de la gravité quantique, qui n'a pas encore été développé (cf. la section sur la gravité quantique , ci-dessous).
Concepts avancés
La structure causale et géométrie globale
Dans la relativité générale, pas de corps matériel peut rattraper ou dépasser une impulsion lumineuse. Aucune influence d'un événement A peut atteindre tout autre endroit X avant la lumière envoyée à A à X. En conséquence, une exploration de toutes les lignes d'univers de lumière ( des géodésiques nulles) donne des informations clés sur la structure causale de l'espace-temps. Cette structure peut être affiché à l'aide de diagrammes de Penrose-Carter dans lequel infiniment grandes régions d'intervalles de temps et d'espace infini sont réduites (" compacifié ") de façon à tenir sur une carte finie, tandis que la lumière voyage toujours le long des diagonales comme dans la norme des diagrammes d'espace-temps.
Conscient de l'importance de la structure causale, Roger Penrose et d'autres ont développé ce qu'on appelle géométrie globale. En géométrie globale, l'objet d'étude est pas un particulier solution (ou famille de solutions) pour les équations d'Einstein. Plutôt, les relations qui détiennent vrai pour tous les géodésiques, comme le Raychaudhuri équation, et les hypothèses non spécifiques supplémentaires sur la nature de la matière (généralement sous la forme de soi-disant conditions d'énergie) sont utilisés pour obtenir des résultats généraux.
Horizons
En utilisant la géométrie globale, certains espaces-temps peuvent être affichés pour contenir limites appelées horizons, qui délimitent une région du reste de l'espace-temps. Les exemples les plus connus sont les trous noirs : si la masse est comprimée dans une région suffisamment compact de l'espace (comme spécifié dans la conjecture de cerceau , l'échelle de longueur pertinent est le rayon de Schwarzschild), pas de lumière à l'intérieur ne peut échapper à l'extérieur. Depuis aucun objet ne peut dépasser une impulsion de lumière, toute la matière intérieure est emprisonné ainsi. Passage de l'extérieur vers l'intérieur est encore possible, ce qui montre que la frontière, du trou noir de l'horizon , est pas une barrière physique.
Les premières études de trous noirs comptaient sur ??????des solutions explicites de l'équation d'Einstein, notamment le sphérique symétrique solution de Schwarzschild (utilisé pour décrire un trou noir statique) et la révolution solution de Kerr (utilisé pour décrire une rotation, trou noir stationnaire, et l'introduction de fonctionnalités intéressantes telles comme le ergosphère). En utilisant la géométrie globale, plus tard, des études ont révélé des propriétés plus générales des trous noirs. À long terme, ils sont plutôt des objets simples caractérisées par onze paramètres spécifiant l'énergie , la quantité de mouvement , moment angulaire , localisation à un moment précis et la charge électrique . Ceci est indiqué par les trous noirs théorèmes d'unicité: "trous noirs ont pas de cheveux", qui est, aucun des signes distinctifs comme les coiffures de l'homme. Indépendamment de la complexité d'un objet gravitant effondrement pour former un trou noir, l'objet que les résultats (après avoir émis des ondes gravitationnelles) est très simple.
Encore plus remarquable, il ya un ensemble général de lois connues comme mécanique de trou noir, qui est analogue aux lois de la thermodynamique. Par exemple, par la deuxième loi de la mécanique de trou noir, la zone de l'horizon d'événement d'un trou noir générale ne sera jamais diminuer avec le temps, analogue à l' entropie d'un système thermodynamique. Cela limite l'énergie qui peut être extraite par des moyens classiques d'un trou noir en rotation (par exemple par le processus Penrose). Il ya des preuves solides que les lois de la mécanique de trou noir sont, en fait, un sous-ensemble des lois de la thermodynamique, et que la zone de trou noir est proportionnelle à son entropie. Cela conduit à une modification des lois originales de mécanique de trou noir: par exemple, que la deuxième loi de mécanique de trou noir devient une partie de la seconde loi de la thermodynamique, il est possible pour la zone du trou noir pour diminuer-tant que les autres processus assurent que, globalement, l'entropie augmente. Comme thermodynamique objets avec la température non nulle, les trous noirs devraient émettre un rayonnement thermique. Calculs semi-classiques indiquent qu'effectivement ils le font, avec la gravité de surface jouant le rôle de la température dans la loi de Planck. Ce rayonnement est connu comme le rayonnement de Hawking (cf. la section de la théorie quantique , ci-dessous).
Il existe d'autres types d'horizons. Dans un univers en expansion, un observateur peut constater que certaines régions du passé ne peuvent être observés (" horizon de particules "), et dans certaines régions de l'avenir ne peuvent pas être influencés (horizon des événements). Même en l'espace de Minkowski plat, lorsque décrite par un observateur accéléré ( Rindler espace), il y aura des horizons associés à un rayonnement semi-classique connu sous le nom radiation Unruh.
Singularités
Une autre caractéristique inquiétante-général et tout à fait de la relativité générale est l'apparition des limites de l'espace-temps connus comme des singularités. Spacetime peut être exploré par le suivi de type temps et de type lumière géodésiques-tous les moyens possibles que la lumière et les particules en chute libre peuvent voyager. Mais certaines solutions des équations d'Einstein ont des «bords déchiquetés"-régions connues comme singularités espace-temps, où les chemins de lumière et de particules tombant viennent à une fin abrupte, et la géométrie devient mal définis. Dans les cas les plus intéressants, ce sont des «singularités courbure", lorsque les quantités géométriques caractérisant l'espace-temps courbe, comme le scalaire de Ricci, prennent des valeurs infinies. Exemples d'espaces-temps bien connu avec les futurs singularités-où d'univers de fin sont la solution de Schwarzschild, qui décrit une singularité à l'intérieur d'un trou noir statique éternelle, ou la solution de Kerr avec sa singularité en forme d'anneau à l'intérieur d'un trou noir en rotation éternelle. Le Friedmann-Lemaître solutions-Walker -Robertson, et d'autres espaces-temps décrivant univers, avoir des singularités dernières lignes d'univers sur lequel commencer, à savoir Big Bang singularités, et certains ont des singularités futures ( big crunch) ainsi.
. Étant donné que ces exemples sont tous très symétrique et donc simplifié-il est tentant de conclure que l'apparition de singularités est un artefact de l'idéalisation Le c??l??bre théorèmes de singularité, se sont révélés en utilisant les méthodes de la géométrie globale, disent le contraire: singularités sont une caractéristique générique du général la relativité, et inévitable une fois l'effondrement d'un objet avec des propriétés de la matière réalistes a procédé au delà d'un certain stade et aussi au début d'une large classe d'élargir univers. Cependant, les théorèmes en disent peu sur les propriétés des singularités, et une grande partie de la recherche actuelle est consacrée à la caractérisation de la structure générique ces entités (l'hypothèse par exemple, par la soi-disant conjecture BKL). Le cosmique hypothèse de censure stipule que toutes les singularités futurs réalistes (pas parfaite symétries, de la matière avec des propriétés réalistes) en toute sécurité sont cachés derrière un horizon, et donc invisible à tous les observateurs lointains. Bien qu'aucune preuve formelle existe encore, des simulations numériques offrent preuves à l'appui de sa validité.
équations d'évolution
Chaque solution de l'équation d'Einstein englobe toute l'histoire d'un univers-il pas seulement certains aperçu de la façon dont les choses sont, mais dans son ensemble, peut-importe-rempli, l'espace-temps. Il décrit l'état de la matière et la géométrie partout et à chaque instant dans cet univers particulier. A ce titre, la théorie d'Einstein semble être différente de la plupart des autres théories physiques, qui spécifient équations d'évolution pour les systèmes physiques: si le système est dans un état ??????donné à un moment donné, les lois de la physique permettent extrapolation dans le passé ou le futur. D'autres différences entre la gravité d'Einstein et d'autres champs sont que le premier est auto-interactive (qui est, non linéaire, même en l'absence d'autres domaines), et qu'il n'a pas de structure-le de fond fixe scène elle-même évolue comme le drame cosmique est épuisé.
Pour comprendre les équations d'Einstein que les équations aux dérivées partielles , il est utile de les formuler d'une manière qui décrit l'évolution de l'univers au fil du temps. Ceci est fait dans ce qu'on appelle "3 + 1" formulations, où l'espace-temps est divisé en trois dimensions spatiales et une dimension temporelle. L'exemple le plus connu est le formalisme ADM. Ces décompositions montrent que les équations d'évolution spatio-temporelles de la relativité générale sont bien comportés: solutions toujours existent, et sont définis de manière unique, une fois les conditions initiales appropriées ont été spécifiés. Ces formulations des équations d'Einstein sont la base de la relativité numérique.
Quantités mondial et quasi-locales
La notion d'équations d'évolution est intimement liée à un autre aspect de la physique relativiste générale. Dans la théorie d'Einstein, il se révèle impossible de trouver une définition générale pour une propriété apparemment simple comme total d'un système de masse (ou l'énergie ). La raison principale est que le champ-comme tout le terrain doit être attribuée physique une certaine énergie, mais qu'il se révèle être fondamentalement impossible de localiser cette énergie gravitationnelle.
Néanmoins, il ya des possibilités pour définir la masse totale d'un système, en utilisant soit un «observateur infiniment éloigné" hypothétique ( de masse ADM) ou symétries appropriés ( de masse Komar). Si l'on exclut de la masse totale du système de l'énergie emportés à l'infini par les ondes gravitationnelles, le résultat est le soi-disant masse Bondi à nulle infini. Tout comme dans la physique classique, il peut être démontré que ces masses sont positifs. Correspondant définitions globales existent pour l'élan et de moment angulaire . On a également un certain nombre de tentatives de définition locale quasi quantités telles que la masse d'un système isolé formulé en utilisant seulement des quantités définies dans une région finie de l'espace contenant ce système. L'espoir est d'obtenir une quantité utile pour des déclarations générales sur les systèmes isolés, comme une formulation plus précise de la conjecture de cerceau.
Relation avec la théorie quantique
Si la relativité générale est considéré comme l'un des deux piliers de la physique moderne, la théorie quantique , la base de notre compréhension de la matière à partir de particules élémentaires à la physique de l'état solide, est l'autre. Cependant, il est encore une question ouverte de la façon dont les concepts de la théorie quantique peuvent être conciliés avec ceux de la relativité générale.
La théorie quantique des champs en espace courbe
Ordinaires théories quantiques des champs , qui forment la base de moderne physique des particules élémentaires , sont définis dans l'appartement l'espace de Minkowski, qui est une excellente approximation quand il vient à décrire le comportement des particules microscopiques dans de faibles champs gravitationnels comme ceux qu'on trouve sur Terre. Afin de décrire des situations dans lesquelles la gravité est assez forte à l'influence (quantique) question, mais pas assez forts pour exiger quantification elle-même, les physiciens ont formulé des théories quantiques des champs en espace-temps courbe. Ces théories reposent sur ??????la relativité générale classique pour décrire un fond courbe l'espace-temps, et de définir une théorie généralisée de champ quantique pour décrire le comportement de la matière quantique dans ce espace-temps. L'utilisation de ce formalisme, il peut être démontré que les trous noirs émettent un spectre de corps noir de particules appelées rayonnement de Hawking , menant à la possibilité qu'ils évaporent au fil du temps. Comme brièvement mentionné ci-dessus , ce rayonnement joue un rôle important pour la thermodynamique des trous noirs.
La gravité quantique
La demande de la cohérence entre une description quantique de la matière et une description géométrique de l'espace-temps, ainsi que l'apparition de singularités (où les échelles de longueur de courbure deviennent microscopique), indiquent la nécessité d'une théorie complète de la gravité quantique: pour une description adéquate de la intérieur des trous noirs, et de l'univers très précoce, une théorie qui est requis dans la gravité et la géométrie de l'espace-temps associés sont décrits dans la langue de physique quantique. Malgré d'importants efforts, aucune théorie complète et cohérente de la gravitation quantique est actuellement connue, même si un certain nombre de candidats prometteurs existe.
Les tentatives visant à généraliser les théories quantiques des champs ordinaires, utilisés dans la physique des particules élémentaires pour décrire les interactions fondamentales, de manière à inclure la gravité ont conduit à de graves problèmes. À basse énergie, cette approche se révèle efficace, en ce qu'elle aboutit à un niveau acceptable (quantique) la théorie du champ de gravité effectif. À de très hautes énergies, cependant, le résultat sont des modèles dépourvus de tout pouvoir prédictif (" non-renormalisabilité ").
Une tentative pour surmonter ces limitations est la théorie des cordes , une théorie quantique pas de particules ponctuelles, mais de minutes objets étendus unidimensionnels. La théorie promet d'être une description unifiée de toutes les particules et les interactions, y compris la gravité; le prix à payer sont des caractéristiques inhabituelles comme six dimensions supplémentaires de l'espace en plus des trois habituels. Dans ce qu'on appelle la deuxième révolution des supercordes, il a été conjecturé que la théorie des cordes et une unification de la relativité générale et la supersymétrie connu comme forme supergravité partie d'un modèle de onze dimensions hypothèse connue comme la théorie-M , ce qui constituerait un sens unique et cohérente théorie de la gravité quantique.
Une autre approche commence par les procédures de quantification canoniques de la théorie quantique. Utilisation de la valeur initiale formulation de la relativité générale (cf. la section sur les équations d'évolution, ci-dessus ), le résultat est le équation de Wheeler-deWitt (un analogue de l' équation de Schrödinger) qui, malheureusement, se révèle être mal définie. Cependant, avec l'introduction de ce qui est maintenant connu sous le nom des variables Ashtekar, ce qui conduit à un modèle prometteur connu comme gravitation quantique à boucles. L'espace est représenté par une structure en forme de bande appelé un réseau de spin, évoluant au fil du temps dans les étapes discrètes.
Selon les caractéristiques de la relativité générale et la théorie quantique sont acceptées inchangée, et à quel niveau les changements sont introduits, il ya de nombreuses autres tentatives pour arriver à une théorie viable de la gravité quantique, certains exemples étant triangulations dynamiques, séries causales,modèles de twisteurs ou lesmodèles basés route intégrante dela cosmologie quantique.
Toutes les théories de candidats ont encore des problèmes majeurs formelles et conceptuelles à surmonter. Ils sont également confrontés au problème commun qui, pour l'instant, il n'y a aucun moyen de mettre les prédictions de la gravité quantique à des essais expérimentaux (et donc de trancher entre les candidats où leurs prédictions varient), mais il ya de l'espoir que cela change les données en tant que futurs de cosmologique observations et des expériences de physique des particules devient disponible.
Statut actuel
La relativité générale est apparue comme un modèle très réussi de la gravitation et de cosmologie, qui a jusqu'ici réussi tous les tests d'observation et d'expérimentation sans ambiguïté. Même si, il ya de fortes indications de la théorie est incomplète. Le problème de la gravité quantique et la question de la réalité de l'espace-temps singularités restent ouverts. Les données d'observation qui est considéré comme une preuve de l'énergie noire et matière noire pourrait indiquer la nécessité d'une nouvelle physique, et alors que la soi-disant Pioneer anomalie pourrait encore admettre une explication conventionnelle, elle aussi, pourrait être un signe avant-coureur d'une nouvelle physique. Même pris tel quel, la relativité générale est riche de possibilités pour une exploration plus poussée. Relativistes mathématiques cherchent à comprendre la nature des singularités et les propriétés fondamentales des équations d'Einstein, et des simulations informatiques de plus en plus puissants (tels que ceux décrivant la fusion des trous noirs) sont exécutés. La course pour la première détection directe des ondes gravitationnelles se poursuit, dans l'espoir de créer des occasions de tester la validité de la théorie des champs gravitationnels beaucoup plus fortes que ce qui a été possible à ce jour. Plus de quatre vingt dix ans après sa publication, la relativité générale reste un domaine très actif de la recherche.
