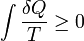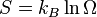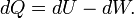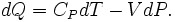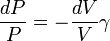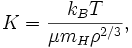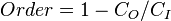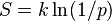Entropy
Contexte des ??coles Wikip??dia
Enfants SOS offrent un chargement complet de la s??lection pour les ??coles pour une utilisation sur les intranets des ??coles. Tous les enfants disponibles pour le parrainage de SOS Enfants des enfants sont pris en charge dans une maison de famille pr??s de la charit??. Lire la suite ...

| Articles Entropy |
|---|
| Introduction |
| Histoire |
| Classique |
| Statistique |
Dans la thermodynamique (une branche de la physique ), l'entropie est une mesure de l'indisponibilit?? d'un de syst??me de l'??nergie ?? faire le travail .
Ce est une mesure du caract??re al??atoire de mol??cules dans un syst??me et est au c??ur de la seconde loi de la thermodynamique et de la la loi combin??e de la thermodynamique, qui traitent avec les processus physiques et se ils se produisent spontan??ment. Changements spontan??s, dans syst??mes isol??s, se produisent avec une augmentation de l'entropie. Changements spontan??s ont tendance ?? lisser les diff??rences de temp??rature , la pression, la densit?? , et potentiel chimique qui peuvent exister dans un syst??me, et l'entropie est donc une mesure de savoir jusqu'o?? ce processus de lissage-out a progress??.
Le mot ??entropie?? est d??riv?? du grec εντροπία "un tournant vers" (εν- "dans" + τροπή "un tournant"), et est symbolis??e par S en physique.
Explication
Lorsque l'??nergie d'un syst??me est d??finie comme la somme de son ??nergie ??utile??, (par exemple celui utilis?? pour pousser un piston), et son ????nergie inutile", ce est ?? dire que l'??nergie qui ne peut ??tre utilis?? pour le travail externe , puis entropie peut ??tre (plus concr??tement) visualis?? comme le "scrap" ou d'??nergie "inutile" dont la pr??valence ??nerg??tique sur l'??nergie totale d'un syst??me est directement proportionnelle ?? la temp??rature absolue de l'consid??r?? syst??me. (Notez les produits "TS" dans le l'??nergie libre de Gibbs ou Helmholtz relations ??nerg??tiques gratuits).
L'entropie est une fonction d'une quantit?? de chaleur qui montre la possibilit?? de conversion de la chaleur en travail. L'augmentation de l'entropie est petite lorsque la chaleur est ajout??e ?? temp??rature ??lev??e et est plus grand lorsque la chaleur est ajout??e ?? une temp??rature inf??rieure. Ainsi, pour l'entropie maximale il ya disponibilit?? minimale pour la conversion en travail et pour entropie minimum il ya une disponibilit?? maximale pour la conversion en travaux.
Sur le plan quantitatif, l'entropie est d??finie par la quantit?? de diff??rentiel  O??
O?? 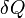 est la quantit?? de chaleur absorb??e dans un isotherme et processus r??versible dans laquelle le syst??me passe d'un ??tat ?? un autre, et T est la temp??rature absolue ?? laquelle le processus est en cours. L'entropie est un des facteurs qui d??termine le l'??nergie libre du syst??me. Cette d??finition thermodynamique de l'entropie ne est valable que pour un syst??me en ??quilibre (parce que la temp??rature est d??finie que pour un syst??me en ??quilibre), alors que la d??finition statistique de l'entropie (voir ci-dessous) se applique ?? ne importe quel syst??me. Ainsi la d??finition statistique est g??n??ralement consid??r?? comme la d??finition fondamentale de l'entropie.
est la quantit?? de chaleur absorb??e dans un isotherme et processus r??versible dans laquelle le syst??me passe d'un ??tat ?? un autre, et T est la temp??rature absolue ?? laquelle le processus est en cours. L'entropie est un des facteurs qui d??termine le l'??nergie libre du syst??me. Cette d??finition thermodynamique de l'entropie ne est valable que pour un syst??me en ??quilibre (parce que la temp??rature est d??finie que pour un syst??me en ??quilibre), alors que la d??finition statistique de l'entropie (voir ci-dessous) se applique ?? ne importe quel syst??me. Ainsi la d??finition statistique est g??n??ralement consid??r?? comme la d??finition fondamentale de l'entropie.
Entropy changement a souvent ??t?? d??finie comme un changement ?? un plus ??tat d??sordonn?? ?? un niveau mol??culaire. Au cours des derni??res ann??es, l'entropie a ??t?? interpr??t?? en termes de " dispersion "de l'??nergie. L'entropie est une extensif fonction d'??tat qui tient compte des effets de irr??versibilit?? syst??mes thermodynamiques.
En termes de m??canique statistique , l'entropie d??crit le num??ro du possible configurations microscopiques du syst??me. La d??finition statistique de l'entropie est la d??finition la plus fondamentale, ?? partir de laquelle toutes les autres d??finitions et toutes les propri??t??s de l'entropie suivent.
Origine du concept de
La premi??re loi de la thermodynamique , formalis?? ?? travers les exp??riences chaleur de friction James Joule en 1843, traite de la notion d'??nergie, qui est conserv?? dans tous les processus; la premi??re loi, toutefois, n'a pas dans sa capacit?? ?? quantifier les effets de frottement et dissipation.
Le concept d'entropie a ??t?? d??velopp?? dans les ann??es 1850 par l'allemand physicien Rudolf Clausius qui l'a d??crit comme la transformation-contenu, ce est ?? dire de dissipation de l'??nergie utilisation, d'un syst??me thermodynamique ou corps de travail esp??ces chimiques lors d'un changement de ??tat.
Bien que le concept d'entropie ??tait ?? l'origine une construction thermodynamique, il a ??t?? adapt?? dans d'autres domaines d'??tudes, y compris th??orie de l'information, psychodynamique, thermo??conomie, et l'??volution .
Histoire

L'histoire de l'entropie commence avec le travail des Fran??ais math??maticien Lazare Carnot qui, dans ses 1803 papier Principes fondamentaux de l'??quilibre et du mouvement propos?? que dans ne importe quelle machine, les acc??l??rations et les chocs des pi??ces en mouvement tous repr??sentent des pertes de moment d'activit??. En d'autres termes, dans tout processus naturel, il existe une tendance inh??rente vers la dissipation d'??nergie utile. Se appuyant sur ce travail, en 1824 le fils de Lazare Sadi Carnot publi?? R??flexions sur la puissance motrice du feu dans lequel il expose le point de vue que, dans tous les moteurs de chaleur chaque fois " calorique ", ou ce qui est maintenant connu comme la chaleur , tombe ?? travers une diff??rence de temp??rature, que le travail ou force motrice peut ??tre produite ?? partir des actions de la ??chute du calorique?? entre un corps chaud et le froid. Ce ??tait un premier aper??u de la seconde loi de la thermodynamique .
Carnot a bas?? ses vues de chaleur en partie sur le d??but du 18e si??cle "hypoth??se newtonienne" que la chaleur et la lumi??re ??taient les types de formes indestructibles de la mati??re, qui sont attir??s et repouss??s par d'autres mati??res, et en partie sur les vues contemporaines de Comte Rumford qui a montr?? en 1789 que la chaleur pourrait ??tre cr???? par le frottement comme lorsque al??sages de canon sont usin??s. En cons??quence, Carnot a estim?? que si le corps de la substance de travail, comme un corps de vapeur d'eau, est ramen?? ?? son ??tat d'origine (de temp??rature et de pression) ?? la fin d'une compl??te cycle du moteur, qui "se produit pas de changement dans l'??tat de l'organe de travail." Ce dernier commentaire a ??t?? modifi?? dans ses notes de bas, et ce est ce commentaire qui a conduit au d??veloppement de l'entropie.
Dans les ann??es 1850 et 60, physicien allemand Rudolf Clausius gravement oppos?? ?? cette derni??re supposition, ce est ?? dire qu'aucun changement ne se produit dans le corps de travail, et a donn?? ce ??changement?? une interpr??tation math??matique en se interrogeant sur la nature de la perte inh??rente de chaleur utilisable lorsque le travail est effectu??, p.ex. chaleur produite par le frottement. Ce ??tait ?? la diff??rence de vues ant??rieures, sur la base des th??ories de Newton , que la chaleur ??tait une particule indestructible qui avait masse. Plus tard, des scientifiques tels que Ludwig Boltzmann, Josiah Willard Gibbs et James Clerk Maxwell ont entropie une base statistique. Carath??odory li??e entropie avec une d??finition math??matique de l'irr??versibilit??, en termes de trajectoires et int??grabilit??.
D??finitions et descriptions
En science, le terme ??entropie?? est g??n??ralement interpr??t?? de trois mani??res distinctes, mais les semi-li??s, ce est ?? dire du point de vue macroscopique ( de la thermodynamique classique ), un point de vue microscopique ( de la thermodynamique statistique ), et un point de vue de l'information ( th??orie de l'information).
La d??finition statistique de l'entropie (voir ci-dessous) est la d??finition fondamentale parce que les deux autres peuvent ??tre math??matiquement en d??coulent, mais pas vice versa. Toutes les propri??t??s de l'entropie (y compris la deuxi??me loi de la thermodynamique ) d??coulent de cette d??finition.
Point de vue macroscopique (thermodynamique classique)
| Variables conjugu??es de la thermodynamique | |
|---|---|
| Pression | Volume |
| ( Stress) | ( Strain) |
| Temp??rature | Entropy |
| Potentiel chimique | nombre de particules |
Dans un syst??me thermodynamique, un ??univers?? constitu?? de ??environnement?? et ??syst??mes?? et compos?? de quantit??s de mati??re, ses diff??rences de pression, les diff??rences de densit??, et les diff??rences de temp??rature tous ont tendance ?? ??galiser dans le temps - tout simplement parce que ??tat d'??quilibre a une plus grande probabilit?? (plus possible combinaisons de micro??tats) que tout autre - voir la m??canique statistique . Dans l' exemple de la fonte des glaces , la diff??rence de temp??rature entre une pi??ce chaude (les abords) et le verre ?? froid de la glace et de l'eau (le syst??me et ne fait pas partie de la pi??ce), commence ?? ??tre ??galis?? que des portions de l'??nergie thermique ?? partir d'un cadre chaleureux ??taler au syst??me de refroidissement de la glace et de l'eau.

Avec le temps, la temp??rature du verre et de son contenu et la temp??rature de la pi??ce devienne ??gale. L'entropie de la salle a diminu?? en partie de son ??nergie a ??t?? dispers?? sur la glace et de l'eau. Cependant, comme calcul?? dans l'exemple, l'entropie du syst??me de glace et d'eau a augment?? de plus de l'entropie de la salle environnante a diminu??. Dans un syst??me isol?? comme la salle et de la glace d'eau pris ensemble, la dispersion de l'??nergie de plus chaud ?? Cooler toujours traduit par une augmentation nette de l'entropie. Ainsi, lorsque le ??univers?? du syst??me d'eau et de glace chambre a atteint un ??quilibre de temp??rature, le changement d'entropie de l'??tat initial est ?? un maximum. L'entropie de la syst??me thermodynamique est une mesure de savoir jusqu'o?? l'??galisation a progress??.
Un cas particulier de l'augmentation de l'entropie, le entropie de m??lange, se produit lorsque deux ou plusieurs substances diff??rentes sont m??lang??s. Si les substances sont ?? la m??me temp??rature et la pression, il n'y aura pas d'??change net de chaleur ou de travail - l'augmentation entropie sera enti??rement d?? au m??lange des diff??rentes substances.
Du point de vue macroscopique, dans la thermodynamique classique l'entropie est interpr??t?? comme un simple fonction d'??tat d'un syst??me thermodynamique: ce est une propri??t?? en fonction seulement de l'??tat actuel du syst??me, ind??pendamment de la fa??on dont cet ??tat est venu ?? ??tre atteint. La fonction d'??tat a la propri??t?? importante qui, lorsqu'il est multipli?? par une temp??rature de r??f??rence, il peut ??tre consid??r?? comme une mesure de la quantit?? d' ??nergie dans un syst??me physique qui ne peut pas ??tre utilis?? pour faire un travail thermodynamique ; ce est ?? dire, le travail m??di??e par l'??nergie thermique. Plus pr??cis??ment, dans tout processus o?? le syst??me donne de l'??nergie Δ E et son entropie diminue de Δ S, une quantit?? au moins T R Δ S de cette ??nergie doit ??tre accord??e ?? l'environnement du syst??me comme inutilisable de chaleur (T R est le temp??rature de milieu ext??rieur du syst??me). Sinon, le processus ne sera pas aller de l'avant.
En 1862, Clausius a d??clar?? ce qu'il appelle le ??th??or??me d'??quivalence en respectant les valeurs des transformations?? ou ce qui est maintenant connu comme le deuxi??me loi de la thermodynamique , comme tel:
- La somme alg??brique de toutes les transformations qui se produisent dans un processus cyclique ne peut ??tre positive, ou, comme un cas extr??me, ??gale ?? rien.
Quantitativement, Clausius indique l'expression math??matique pour ce th??or??me est le suivant. Soit AQ un ??l??ment de la chaleur d??gag??e par le corps ?? ne importe quel r??servoir de chaleur au cours de ses variations, la chaleur qui peut absorber ?? partir d'un r??servoir ??tant compt?? comme ici n??gatif, et T la temp??rature absolue du corps au moment de donner cette chaleur, alors l'??quation:
doit ??tre vrai pour tous les processus cyclique r??versible, et la relation:
doit d??tenir bon pour tous les processus cyclique qui est de toute fa??on possible. Ce est la formulation essentiel de la seconde loi et l'une des formes d'origine du concept de l'entropie. On voit que les dimensions de l'entropie sont l'??nergie divis??e par la temp??rature, qui est la m??me que les dimensions de La constante de Boltzmann (k B) et la capacit?? calorifique. Le Unit?? SI de l'entropie est " joule par kelvin ??(J ?? K -1). De cette mani??re, la quantit??" ΔS "est utilis?? comme un type d'??nergie interne, qui repr??sente les effets de irr??versibilit??, dans l'??quation de l'??quilibre ??nerg??tique de tout syst??me. Dans l' ??nergie libre Gibbs ??quation, ?? savoir AG = AH - TΔS, par exemple, qui est une formule couramment utilis??e pour d??terminer si les r??actions chimiques se produisent, l'??nergie li??e ?? l'entropie changements TΔS est soustraite de la AH "total" d'??nergie du syst??me pour donner le "libre" Ag d'??nergie du syst??me, comme au cours d'une processus chimique ou comme quand un syst??me change d'??tat.
D??finition microscopique de l'entropie (m??canique statistique)
Dans la thermodynamique statistique de l'entropie est d??fini comme le nombre de configurations microscopiques qui se traduisent par la observ??s description macroscopique du syst??me thermodynamique:
o??
- k B est Constante 1,38066 ?? 10 -23 J K -1 et de Boltzmann
-
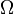 est le nombre de micro??tats correspondant ?? la macro-thermodynamique observ??e.
est le nombre de micro??tats correspondant ?? la macro-thermodynamique observ??e.
Cette d??finition est consid??r?? comme la d??finition fondamentale de l'entropie (comme toutes les autres d??finitions peuvent ??tre d??riv??es d'math??matiquement, mais pas vice versa). En 1896 Conf??rences de Boltzmann sur la th??orie des gaz, il a montr?? que cette expression donne une mesure de l'entropie pour les syst??mes d'atomes et de mol??cules dans la phase gazeuse, fournissant ainsi une mesure de l'entropie de la thermodynamique classique.
En 1877, Boltzmann visualis?? de mani??re probabiliste pour mesurer l'entropie d'un ensemble de particules de gaz parfaits, dont il a d??fini l'entropie d'??tre proportionnelle au logarithme du nombre de micro-un tel gaz pourrait occuper. D??sormais, le probl??me essentiel dans la thermodynamique statistique , ce est ?? dire en fonction de Erwin Schr??dinger, a ??t?? de d??terminer la distribution d'une quantit?? d'??nergie donn??e E sur N syst??mes identiques.
La m??canique statistique explique entropie comme la quantit?? d'incertitude (ou "mixedupness?? dans l'expression de Gibbs ) qui reste d'un syst??me, d'apr??s ses propri??t??s macroscopiques observables ont ??t?? prises en compte. Pour un ensemble donn?? de variables macroscopiques, comme la temp??rature et le volume, l'entropie mesure le degr?? auquel la probabilit?? que le syst??me est r??parti sur les diff??rents ??tats quantiques possibles. Les plus ??tats disponibles dans le syst??me avec une probabilit?? plus ??lev??e, plus la entropie. Plus pr??cis??ment, l'entropie est une mesure logarithmique de la densit?? d'??tats. En substance, l'interpr??tation la plus g??n??rale de l'entropie est une mesure de l'incertitude sur notre syst??me. Le ??tat d'un syst??me d'??quilibre maximise l'entropie parce que nous avons perdu toutes les informations sur les conditions initiales, sauf pour les variables conserv??es; maximisant l'entropie maximise notre ignorance sur les d??tails du syst??me. Cette incertitude ne est pas du genre subjective de tous les jours, mais plut??t de l'incertitude inh??rente ?? la m??thode exp??rimentale et mod??le interpr??tatif.
?? l'??chelle mol??culaire, les deux d??finitions correspondent parce ajoutant de la chaleur ?? un syst??me, ce qui augmente son entropie thermodynamique classique, augmente ??galement du syst??me fluctuations thermiques , donnant ainsi un manque accru d'informations sur l'??tat microscopique exacte du syst??me, ce est ?? dire une augmentation de la entropie m??canique statistique.
Le mod??le interpr??tatif a un r??le central dans la d??termination de l'entropie. Le qualificatif "pour un ensemble donn?? de variables macroscopiques?? ci-dessus a des implications tr??s profondes: si deux observateurs utilisent diff??rents ensembles de variables macroscopiques, alors ils observeront diff??rentes entropies. Par exemple, si l'observateur A utilise les variables U, V et W, et l'observateur B utilise U, V, W, X, puis, en changeant X, l'observateur B peut provoquer un effet qui ressemble ?? une violation de la deuxi??me loi de la thermodynamique d'observateur A. En d'autres termes: l'ensemble des variables macroscopiques on choisit doit inclure tout ce qui peut changer dans l'exp??rience, sinon on pourrait voir diminuer l'entropie!
Entropie en thermodynamique chimiques
Entropie thermodynamique est central dans thermodynamique chimique, permettant de quantifier les changements et les r??sultats des r??actions pr??visibles. La seconde loi de la thermodynamique indique que l'entropie de la combinaison d'un syst??me et de son environnement (ou dans une syst??me isol?? par lui-m??me) augmente pendant tous les processus chimiques et physiques spontan??es. Spontan??it?? dans la chimie signifie "par lui-m??me, ou sans aucune influence ext??rieure", et n'a rien ?? voir avec la vitesse. L'??quation de Clausius des δ q tr / T = Δ S introduit la mesure du changement d'entropie, Δ S. Changement entropie d??crit la direction et quantifie l'ampleur des changements simples tels que la chaleur transfert entre syst??mes - toujours du plus chaud ?? Cooler spontan??ment. Ainsi, lorsqu'un mole de substance ?? 0 K est r??chauff??e par son environnement ?? 298 K, la somme des valeurs incr??mentielles de q tr / T constituent de chaque ??l??ment ou entropie molaire standard du compos??, une propri??t?? physique fondamentale et un indicateur de la quantit?? d'??nergie stock??e par un substance ?? 298 K. changement d'entropie mesure ??galement le m??lange de substances correspondant ?? la somme de leurs quantit??s relatives dans le m??lange final.
Entropy est ??galement essentiel de pr??voir l'ampleur des r??actions chimiques complexes, ?? savoir si un processus ira ??crite ou de proc??der dans la direction oppos??e. Pour de telles applications, Δ S doit ??tre incorpor?? dans une expression qui inclut ?? la fois le syst??me et ses environs, Δ de l'univers = environnement syst??me + S Δ de Δ. Cette expression devient, par l'interm??diaire de certaines ??tapes, l' ??nergie libre Gibbs ??quation pour r??actifs et des produits dans le syst??me: Δ G [l' ??nergie libre de Gibbs changement du syst??me] = Δ H [l' enthalpie changement] - T Δ S [le changement d'entropie] .
La deuxi??me loi
Un important loi de la physique, de la seconde loi de la thermodynamique , stipule que l'entropie totale de tout syst??me thermodynamique isol?? tend ?? augmenter au fil du temps, l'approche d'une valeur maximale; et donc, par voie de cons??quence, l'entropie de l'univers (ce est ?? dire le syst??me et ses environs), pris comme un syst??me isol??, tend ?? augmenter. Deux cons??quences importantes sont que la chaleur ne peut pas lui-m??me passer d'un froid ?? un corps chaud: ce est ?? dire, il est impossible de transf??rer la chaleur d'un endroit froid ?? un r??servoir ?? chaud sans en m??me temps la conversion d'une certaine quantit?? de travail ?? la chaleur. Il est ??galement impossible pour ne importe quel appareil qui peut fonctionner sur un cycle pour recevoir la chaleur ?? partir d'un seul r??servoir et de produire un montant net de travail; il ne peut obtenir un travail utile sur la chaleur si la chaleur est en m??me temps transf??r?? d'une chaude ?? un r??servoir froid. Cela signifie qu'il n'y a pas possibilit?? d'une isol?? " perp??tuel "syst??me de mouvement. De plus, ?? partir de cela, il se ensuit que la r??duction de l'augmentation de l'entropie dans un proc??d?? sp??cifi??, tel qu'une r??action chimique , signifie qu'il est ??nerg??tiquement plus efficace.
En g??n??ral, selon la seconde loi, l'entropie d'un syst??me qui ne est pas isol?? peut diminuer. Une climatiseur, par exemple, refroidit l'air dans une pi??ce, ce qui r??duit l'entropie de l'air. La chaleur, cependant, impliqu??s dans le fonctionnement du climatiseur fait toujours une plus grande contribution ?? l'entropie de l'environnement que la diminution de l'entropie de l'air. Ainsi l'entropie totale de la salle et l'environnement augmente, en accord avec la deuxi??me loi.
??quation d'??quilibre entropie pour les syst??mes ouverts
En g??nie chimique, les principes de la thermodynamique sont couramment appliqu?? ?? " syst??mes ouverts ", ce est ?? dire ceux dans lesquels la chaleur , le travail et la masse ??coulement ?? travers les limites du syst??me. Dans un syst??me dans lequel il existe des flux de la chaleur (  ) Et le travail, ce est-
) Et le travail, ce est- 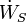 (Travail sur l'arbre) et P (dV / dt) (travail pression-volume), dans les limites du syst??me, le flux de chaleur, mais pas le flux de travail, entra??ne une modification de l'entropie du syst??me. Ce taux de variation d'entropie est
(Travail sur l'arbre) et P (dV / dt) (travail pression-volume), dans les limites du syst??me, le flux de chaleur, mais pas le flux de travail, entra??ne une modification de l'entropie du syst??me. Ce taux de variation d'entropie est  o?? T est l'absolu temp??rature thermodynamique du syst??me ?? l'endroit de l'??coulement de chaleur. Si, en plus, il existe des flux de masse ?? travers les limites du syst??me, l'entropie totale du syst??me sera ??galement changer en raison de ce flux de convection.
o?? T est l'absolu temp??rature thermodynamique du syst??me ?? l'endroit de l'??coulement de chaleur. Si, en plus, il existe des flux de masse ?? travers les limites du syst??me, l'entropie totale du syst??me sera ??galement changer en raison de ce flux de convection.

Pour d??river une ??quation ??quilibr??e entropie g??n??ralis??e, nous commen??ons par l'??quation d'??quilibre g??n??ral pour le changement dans toute Θ vaste quantit?? dans un syst??me thermodynamique, une quantit?? qui peut ??tre soit conserv??e, comme l'??nergie, ou non conserv??, comme l'entropie. L'expression g??n??rique de base de la balance indique que dΘ / dt, ce est ?? dire le taux de variation de Θ dans le syst??me, est ??gale ?? la vitesse ?? laquelle Θ entre dans le syst??me au niveau des joints, moins la vitesse ?? laquelle Θ quitte le syst??me ?? travers les limites du syst??me, ainsi que la vitesse ?? laquelle Θ est g??n??r?? dans le syst??me. En utilisant cette ??quation d'??quilibre g??n??rique, en ce qui concerne le taux de variation dans le temps de la grande quantit?? d'entropie S, l'??quation du bilan d'entropie pour un syst??me thermodynamique est ouvert:
o??
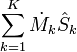 = Le taux net de flux d'entropie due aux flux de masse dans et hors du syst??me (o??
= Le taux net de flux d'entropie due aux flux de masse dans et hors du syst??me (o??  = Entropie par unit?? de masse).
= Entropie par unit?? de masse).
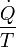 = Le d??bit d'??coulement d'entropie due ?? l'??coulement de chaleur ?? travers la limite du syst??me.
= Le d??bit d'??coulement d'entropie due ?? l'??coulement de chaleur ?? travers la limite du syst??me.
 = La vitesse de g??n??ration interne d'entropie dans le syst??me.
= La vitesse de g??n??ration interne d'entropie dans le syst??me.
Notez aussi que se il ya plusieurs flux de chaleur, le terme 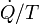 est destin??e ?? ??tre remplac??e par
est destin??e ?? ??tre remplac??e par  o??
o??  est le flux de chaleur et
est le flux de chaleur et 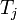 est la temp??rature ?? l'orifice d'??coulement de chaleur ji??me dans le syst??me.
est la temp??rature ?? l'orifice d'??coulement de chaleur ji??me dans le syst??me.
Entropie en m??canique quantique (von Neumann entropie)
En m??canique statistique quantique, le concept d'entropie a ??t?? d??velopp?? par John von Neumann et est g??n??ralement appel?? "l'entropie de von Neumann". Von Neumann a ??tabli le cadre math??matique correct pour la m??canique quantique avec son travail Mathematische Grundlagen der Quantenmechanik. Il a fourni dans ce travail d'une th??orie de la mesure, o?? la notion habituelle de l'effondrement d'onde est d??crit comme un processus irr??versible (la soi-disant von Neumann ou de mesure projective). En utilisant ce concept, en liaison avec le matrice densit?? il a ??tendu le concept classique de l'entropie dans le domaine quantique.
Il est bien connu que la d??finition de l'information bas??e entropie de Shannon conduit dans le cas classique de l'entropie de Boltzmann. Il est tentant de consid??rer l'entropie de Von Neumann que la d??finition de la m??canique quantique correspondante. Mais celui-ci est probl??matique du point de vue quantique de l'information. Par cons??quent Stotland, Pomeransky, Bachmat et Cohen ont introduit une nouvelle d??finition de l'entropie qui refl??te l'incertitude inh??rente aux ??tats quantiques. Cette d??finition permet de distinguer entre l'entropie d'incertitude minimum de l'??tat pur, et l'exc??s entropie statistique de m??langes.
Entropie en astrophysique
En astrophysique, ce qui est appel?? ??l'entropie?? est en fait la constante adiabatique calcul??e comme suit.
Utilisation de la premi??re loi de la thermodynamique pour un processus infinit??simale quasi-statique d'un syst??me hydrostatique
Pour un gaz parfait dans ce cas particulier, l'??nergie interne, U, est seulement une fonction de T; par cons??quent la d??riv??e partielle de la capacit?? de chaleur par rapport ?? T est identiquement la m??me chose que le d??riv?? complet, ce qui donne par quelques manipulations
Autre manipulation en utilisant la version diff??rentielle de la loi des gaz parfaits, l'??quation pr??c??dente, et en supposant une pression constante, on trouve
Pour un processus adiabatique  et rappelant
et rappelant  , On trouve
, On trouve
On peut r??soudre cette ??quation diff??rentielle simple ?? trouver
Cette ??quation est connue comme une expression de la constante adiabatique, K, aussi appel?? le adiabatique. De l'??quation des gaz parfaits on sait aussi
o??  est la constante de Boltzmann. En substituant cette dans l'??quation ci-dessus avec
est la constante de Boltzmann. En substituant cette dans l'??quation ci-dessus avec ![V = [g] / \ rho](../../images/175/17559.png) et
et 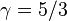 pour un gaz monoatomique id??al on trouve
pour un gaz monoatomique id??al on trouve
o?? 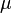 est le poids mol??culaire moyen du gaz ou du plasma; et
est le poids mol??culaire moyen du gaz ou du plasma; et 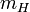 est la masse de l'atome d'hydrog??ne, qui est tr??s proche de la masse du proton,
est la masse de l'atome d'hydrog??ne, qui est tr??s proche de la masse du proton, 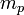 , La quantit?? le plus souvent utilis??e dans la th??orie astrophysique des amas de galaxies. Ce est ce que astrophysiciens se r??f??rer ?? "l'entropie" et dispose d'unit??s de [keV cm 2]. Cette quantit?? se rapporte ?? l'entropie thermodynamique
, La quantit?? le plus souvent utilis??e dans la th??orie astrophysique des amas de galaxies. Ce est ce que astrophysiciens se r??f??rer ?? "l'entropie" et dispose d'unit??s de [keV cm 2]. Cette quantit?? se rapporte ?? l'entropie thermodynamique
o?? 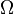 , La densit?? d'??tats dans la th??orie statistique, prend la valeur de K tel que d??fini ci-dessus.
, La densit?? d'??tats dans la th??orie statistique, prend la valeur de K tel que d??fini ci-dessus.
D??finitions de manuels standard
Ce qui suit est une liste de d??finitions de l'entropie d'une collection de manuels. Notez que les d??finitions de manuels scolaires ne sont pas toujours les d??finitions les plus utiles, mais ils sont un aspect important de la culture entourant la notion d'entropie.
- Entropie - ??nergie ventil??s irr??m??diable chaleur .
- Constante fois de Boltzmann le logarithme d'une multiplicit??; o?? la multiplicit?? d'une macroscopique est le nombre de microscopiques qui correspondent ?? l'??tat macroscopique.
- le nombre de fa??ons d'arranger les choses dans un syst??me (les temps La constante de Boltzmann).
- un thermodynamique de non conserv?? fonction d'??tat, mesur??e en termes de nombre de un syst??me micro-peuvent prendre, ce qui correspond ?? une d??gradation utilisable ??nergie .
- une mesure directe de la al??atoire d'un syst??me.
- une mesure de dispersion d'??nergie ?? une temp??rature sp??cifique.
- une mesure de la perte partielle de la capacit?? d'un syst??me ?? ex??cuter un travail en raison des effets de irr??versibilit??.
- un indice de la tendance vers un syst??me de changement spontan??.
- une mesure de l'indisponibilit?? de l'??nergie d'un syst??me pour faire le travail; ??galement une mesure de d??sordre; l'entropie la plus ??lev??e plus le trouble.
- un param??tre repr??sentant l'??tat de trouble d'un syst??me ?? l'??chelle atomique, ionique ou mol??culaire.
- une mesure du trouble ou de l'univers de la disponibilit?? de l'??nergie dans un syst??me ?? faire le travail.
Les approches de compr??hension entropie
Ordre et d??sordre
L'entropie, historiquement, a souvent ??t?? associ?? ?? la quantit?? de afin, trouble, et / ou dans un chaos syst??me thermodynamique. La d??finition traditionnelle de l'entropie, ce est qu'il se r??f??re ?? des changements dans le statu quo du syst??me et est une mesure de "d??sordre mol??culaire" et la quantit?? d'??nergie gaspill??e dans une transformation de l'??nergie dynamique d'un ??tat ou une forme ?? l'autre. En ce sens, un certain nombre d'auteurs, au cours des derni??res ann??es, ont d??riv?? formules d'entropie exactes de comptabiliser et de mesurer le trouble et l'ordre dans les assembl??es atomiques et mol??culaires. Une des formules plus simples afin entropie / trouble est celle d??riv??e en 1984 par le physicien Peter thermodynamique Landsberg, qui est bas?? sur une combinaison de la thermodynamique et arguments de la th??orie de l'information. Landsberg affirme que lorsque les contraintes fonctionnent sur un syst??me, de telle sorte qu'elle est emp??ch??e d'entrer dans une ou plusieurs de ses ??tats possibles ou permises, par opposition ?? ses ??tats interdits, la mesure de la quantit?? totale de "trouble" dans le syst??me est donn??e par l'expression suivante:
De m??me, la quantit?? totale de "commande" dans le syst??me est donn??e par:
Dans lequel C D est le "d??sordre" capacit?? du syst??me, qui est l'entropie des pi??ces contenues dans l'ensemble permis, C I est l '"information" capacit?? du syst??me, une expression similaire ?? Shannon la capacit?? du canal, et C O est "l'ordre" capacit?? du syst??me.
Dispersion d'??nergie
Le concept d'entropie peut ??tre d??crit qualitativement comme une mesure de la dispersion d'??nergie ?? une temp??rature donn??e. Termes similaires ont ??t?? en usage d??s le d??but de l'histoire de la thermodynamique classique , et avec le d??veloppement de la thermodynamique statistique et la th??orie quantique , les changements entropie ont ??t?? d??crits en termes de m??lange ou de "diffusion" de l'??nergie totale de chaque constituant d'un syst??me sur ses niveaux d'??nergie quantifi??s particuliers.
Ambigu??t??s dans les termes d??sordre et le chaos, qui ont g??n??ralement le sens directement oppos??s ?? l'??quilibre, contribuent ?? une grande confusion et entravent la compr??hension de l'entropie pour la plupart des ??tudiants. Comme la seconde loi de la thermodynamique montre, en syst??me isol?? parties internes ?? diff??rentes temp??ratures auront tendance ?? se adapter ?? une temp??rature uniforme unique et donc de produire ??quilibre. Une approche ??ducative r??cemment d??velopp?? ??vite les termes ambigus et d??crit comme ??talement de l'??nergie que la dispersion, ce qui conduit ?? la perte des ??carts n??cessaires pour le travail, m??me si l'??nergie totale reste constante en conformit?? avec la premi??re loi de la thermodynamique . Physico-chimiste Peter Atkins, par exemple, qui a d??j?? ??crit de la dispersion conduisant ?? un ??tat d??sordonn??, ??crit maintenant que "des changements spontan??s sont toujours accompagn??s par une dispersion de l'??nergie", et a jet?? ??d??sordre?? comme une description.
la th??orie de l'entropie et de l'information
En th??orie de l'information, l'entropie est la mesure de la quantit?? d'informations qui est absent avant r??ception et est parfois appel??e entropie de Shannon. Entropie de Shannon est un concept large et g??n??ral qui trouve des applications dans th??orie de l'information, ainsi que la thermodynamique. Il a ??t?? initialement con??u par Claude Shannon en 1948 pour ??tudier la quantit?? d'informations dans un message transmis. La d??finition de l'entropie de l'information est, cependant, tout ?? fait g??n??ral, et est exprim?? en termes d'un ensemble discret de probabilit??s  . Dans le cas des messages transmis, ces probabilit??s ??taient les probabilit??s qu'un message particulier a ??t?? effectivement transmis, et l'entropie du syst??me de messagerie ??tait une mesure de la quantit?? d'information dans le message. Pour le cas des probabilit??s ??gales (ce est ?? dire chaque message est tout aussi probable), l'entropie de Shannon (en bits) ne est que le nombre de questions oui / non n??cessaires pour d??terminer le contenu du message.
. Dans le cas des messages transmis, ces probabilit??s ??taient les probabilit??s qu'un message particulier a ??t?? effectivement transmis, et l'entropie du syst??me de messagerie ??tait une mesure de la quantit?? d'information dans le message. Pour le cas des probabilit??s ??gales (ce est ?? dire chaque message est tout aussi probable), l'entropie de Shannon (en bits) ne est que le nombre de questions oui / non n??cessaires pour d??terminer le contenu du message.
La question du lien entre l'entropie de l'information et l'entropie thermodynamique est un sujet chaudement d??battu. Certains auteurs soutiennent qu'il ya un lien entre les deux, tandis que d'autres diront qu'ils ne ont absolument rien ?? voir avec l'autre.
Les expressions pour les deux entropies sont tr??s similaires. Les informations entropie H pour des probabilit??s ??gales  est:
est:
o?? K est une constante qui d??termine les unit??s de l'entropie. Par exemple, si les unit??s sont des bits, alors K = 1 / ln (2). La thermodynamique entropie S, d'un point de vue m??canique statistique a ??t?? exprim??e par Boltzmann:
o?? p est la probabilit?? d'un syst??me ??tant dans un ??tat microscopique particulier, ??tant donn?? qu'il est dans un ??tat macroscopique particulier, et k est la constante de Boltzmann. On peut voir que l'on peut penser de l'entropie thermodynamique constante, divis?? par ln (2), multipli?? par le nombre de Boltzmann des questions oui / non qui doivent ??tre pos??es afin de d??terminer l'??tat microscopique du syst??me, ??tant donn?? que nous savons que les macroscopique. Le lien entre l'entropie thermodynamique et de l'information a ??t?? d??velopp?? dans une s??rie de documents par Edwin Jaynes ?? partir de 1957.
Le probl??me avec reliant entropie thermodynamique ?? l'information entropie, ce est que l'information entropie l'ensemble du corps de la thermodynamique qui traite de la nature physique de l'entropie est manquant. La deuxi??me loi de la thermodynamique qui r??git le comportement des syst??mes thermodynamiques ?? l'??quilibre, et la premi??re loi qui exprime l'??nergie thermique que le produit de la temp??rature et l'entropie sont des concepts physiques plut??t que des concepts d'information. Si l'entropie thermodynamique est consid??r?? comme incluant toutes les dynamiques physiques de l'entropie ainsi que les aspects statistiques d'??quilibre, l'information entropie donne qu'une partie de la description de l'entropie thermodynamique. Certains auteurs, comme Tom Schneider, plaident en faveur de la suppression du terme entropie pour la fonction H de la th??orie de l'information et l'aide d'autres terme ??incertitude?? de Shannon ?? la place.
exemple de fusion de la glace
L'illustration de cet article est un exemple classique dans laquelle l'entropie augmente dans un petit ??univers??, un syst??me thermodynamique constitu?? de la (la pi??ce chaude) ??des alentours?? et ??syst??me?? (verre, glace, eau froide). Dans cet univers, certains chaleur AQ de l'??nergie ?? partir de l'environnement de pi??ce plus chaude (?? 298 K ou 25 ?? C) se propage vers le syst??me de refroidissement de la glace et de l'eau ?? sa temp??rature constante T de 273 K (0 ?? C), la temp??rature de fusion de glace. L'entropie du syst??me va changer par la quantit?? dS = AQ / T, dans cet exemple AQ / 273 K. (La AQ de chaleur pour ce processus est l'??nergie n??cessaire pour changer l'eau de l'??tat solide ?? l'??tat liquide, et est appel?? la enthalpie de fusion, à savoir le ??H. pour la fusion de la glace) L'entropie de l'environnement change par une quantitédS= -AQ/ 298 K. Ainsi, dans cet exemple, l'entropie du système augmente, tandis que l'entropie de l'environnement diminue .
Il est important de réaliser que la diminution de l'entropie de la salle environnante est inférieure à l'augmentation de l'entropie de la glace et de l'eau: la température ambiante de 298 K est supérieure à 273 K, et donc le rapport, (changement d'entropie), d' AQ / 298 K pour l'environnement est plus petit que le rapport (changement d'entropie), de AQ / 273 K pour la glace système d'eau +. Pour trouver le changement d'entropie de notre «univers», nous additionnons les changements d'entropie pour ses mandants: la salle environnante, et la glace + eau. Le changement d'entropie totale est positive; cela est toujours le cas dans les événements spontanés dans un système thermodynamique et il montre l'importance prédictive de l'entropie: l'entropie net final après un tel événement est toujours plus grande que ne l'était l'entropie initiale.
Comme la température de l'eau fraîche se lève à celle de la chambre et la salle refroidit encore imperceptiblement, la somme de l' AQ / T sur la plage continue, à de nombreux paliers, d'abord dans le froid pour finalement l'eau chaude peut être trouvé par le calcul. La miniature toute «univers», à savoir ce système thermodynamique, l'entropie a augmenté. Energy a spontanément devenir plus dispersée et se propager dans cette «univers» que lorsque le verre d'eau glacée a été introduit et est devenu un «système» en son sein.
Sujets de l'entropie
Entropie et de la vie
Depuis plus d'un siècle et demi, en commençant par 1 863 mémoires de Clausius "sur la concentration des rayons de chaleur et de lumière, et sur ??????les limites de son action", beaucoup d'écriture et de recherche a été consacrée à la relation entre l'entropie thermodynamique et l' évolution de la vie . L'argument selon lequel la vie se nourrit de l'entropie négative ou néguentropie comme mis en avant dans le livre 1944 What is Life? par physicien Erwin Schrödinger a servi de nouvelles mesures de relance à cette recherche. Écrits récents ont utilisé le concept de Gibbs l'énergie libre d'élaborer sur cette question. Tangentiellement, certains créationnistes ont fait valoir que l'entropie exclut évolution .
En 1982 manuels populaires Principles of Biochemistry par biochimiste américain a noté Albert Lehninger, par exemple, il est soutenu que l' ordre produit dans les cellules comme ils croissent et se divisent est plus que compensée par le désordre qu'ils créent dans leur environnement au cours de la croissance et la division. En bref, selon Lehninger, "organismes vivants conservent leur ordre interne en prenant de leur environnement de l'énergie libre, sous la forme de nutriments ou de la lumière du soleil, et de retourner à leur environnement une quantité égale de l'énergie comme la chaleur et l'entropie. "
Evolution li??es d??finitions:
- Néguentropie- une phrase familière raccourci pour l'entropie négative.
- Ectropy- une mesure de la tendance d'un système dynamique de faire un travail utile et croître plus organisée.
- Syntropy- une tendance vers l'ordre et des combinaisons symétriques et les dessins de modèles de plus en plus avantageuses et ordonnée.
- Extropy- un terme métaphorique définir l'étendue de la vie ou l'intelligence de système organisationnel, par ordre fonctionnel, la vitalité, l'énergie, la vie, l'expérience et la capacité et l'entraînement pour l'amélioration et la croissance.
- Entropie écologique- une mesure dela biodiversitédans l'étude de la diversité biologiquede l'écologie.
La flèche du temps
L'entropie est la seule quantité dans les sciences physiques que les «pics» une direction particulière pour le temps, parfois appelé une flèche du temps. Comme nous allons "avant" dans le temps, la deuxième loi de la thermodynamique nous dit que l'entropie d'un système isolé ne peut augmenter ou rester la même; il ne peut pas diminuer. Ainsi, d'un point de vue, la mesure entropie est considéré comme une sorte d'horloge.
Entropie et de la cosmologie
Comme un univers fini peut être considéré comme un système isolé, il peut être soumis à la deuxième loi de la thermodynamique, de sorte que son entropie totale augmente constamment. Il a été spéculé que l'univers est voué à une mort de chaleur dans lequel tout l' énergie finit en une répartition homogène de l'énergie thermique, de sorte que pas plus de travail peut être extrait d'une source quelconque.
Si l'univers ne peut être considéré comme ayant généralement entropie croissante, puis - comme Roger Penrose l'a souligné - gravité joue un rôle important dans l'augmentation parce que la gravité provoque la matière dispersée à accumuler en étoiles, qui chute finalement dans les trous noirs . Jacob Bekenstein et Stephen Hawking ont montré que les trous noirs ont l'entropie maximale possible de tout objet de taille égale. Cela fait d'eux des points finaux probables de tous les processus d'entropie croissante, si elles sont matière et d'énergie pièges totalement efficaces. Hawking a, cependant, a récemment changé sa position sur cet aspect.
Le rôle de l'entropie en cosmologie reste un sujet controversé. Des travaux récents ont jeté le doute sur la vaste hypothèse de la mort de la chaleur et de l'applicabilité de tout modèle thermodynamique simple à l'univers en général. Bien que l'entropie ne augmentation dans le modèle d'un univers en expansion, l'entropie maximale possible augmente beaucoup plus rapidement - donc la densité entropie diminue avec le temps. Il en résulte un "écart de l'entropie" pousser le système plus loin de l'équilibre. Autres facteurs aggravants, tels que la densité d'énergie du vide et macroscopiques quantiques effets, sont difficiles à concilier avec les modèles thermodynamiques, de faire des prévisions de la thermodynamique à grande échelle extrêmement difficile.
Autres relations
Autres définitions mathématiques
- Kolmogorov-Sinai entropie- un type mathématique de l'entropie dansles systèmes dynamiques liées aux mesures de partitions.
- Entropie topologique- une façon de définir l'entropie dans une carte de fonction itérée th??orie ergodique.
- Entropie relative- est une mesure de distance naturelle à partir d'un "vrai" distribution de probabilitéPà un arbitraire distribution de probabilitéQ.
- Entropie Rényi- une mesure de l'entropie généralisée pour les systèmes fractales.
Définitions sociologiques
Le concept d'entropie a également pénétré le domaine dela sociologie, généralement comme unemétaphore pour le chaos, le désordre ou la dissipation de l'énergie, plutôt que comme une mesure directe de l'entropie thermodynamique ou de l'information:
- Entropology- l'étude ou de discussion de l'entropie ou le nom parfois donné àla thermodynamiquesanséquations différentielles.
- Entropie psychologique- la distribution d'énergie dans la psyché, ce qui tend à rechercher l'équilibre ou équilibre entre toutes les structures de la psyché.
- Entropie économique- une mesure semi-quantitative de la dissipation irrévocable et la dégradation de matériaux naturels et de l'énergie disponible par rapport à l'activité économique.
- Entropie sociale - une mesure de la structure du système social, ayant deux interprétations théoriques et statistiques, à savoir la société (variables macrosociétales) mesurée en termes de la façon dont les différentes fonctions dans la société (variables microsocietal); également liée à l'équilibre social.
- Entropie d'entreprise - le gaspillage d'énergie que les formalités administratives et de l'équipe entreprise inefficacité, à savoir l'énergie perdue à perdre. (Cette définition est comparable à la notion de von Clausewitz de friction dans la guerre.)
Citations
| " | Toute méthode impliquant la notion del'entropie, l'existence même de ce qui dépend de ladeuxième loi de la thermodynamique, semblera sans doute pour beaucoup exagéré, et peut repousser les débutants comme obscure et difficile à comprendre. | " |
- -Willard Gibbs,méthodes graphiques dans la thermodynamique des fluides(1873)
| " | Ma plus grande préoccupation était comment l'appeler. Je pensais l'appeler «information», mais le mot a été trop utilisé, donc je décidai de l'appeler «l'incertitude». Quand je discuté avec John von Neumann , il avait une meilleure idée. Von Neumann m'a dit, 'Vous devez appeler l'entropie , pour deux raisons. En premier lieu, votre fonction d'incertitude a été utilisé dans la mécanique statistique sous ce nom, il a déjà un nom. En second lieu, et plus important encore, personne ne sait ce que l'entropie est vraiment, donc dans un débat que vous aurez toujours l'avantage. | " |
- --Conversation EntreClaude Shannon etJohn von Neumannau sujet de ce nom à donner à la «mesure de l'incertitude" ou l'atténuation des signaux de la ligne téléphonique (1949)
| " | Chaque étoile qui brûle, chaque planète dont l'orbite est lentement en décomposition, chaque souffle que vous prenez et en calories à métaboliser apporte l'univers de plus en plus près du point où l'entropie est maximisée, mouvement organisé de toute sorte cesse, et rien ne se reproduise plus jamais. On ne peut échapper. Peu importe combien magnifique vie dans l'univers devient ou comment avancée, la lente augmentation de l'entropie ne peut être arrêtée - l'univers finira par mourir. | " |
- --Warren Friedl, Université de Windsor (2007)