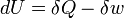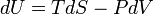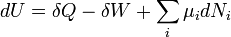Premi??re loi de la thermodynamique
Renseignements g??n??raux
Les articles de cette s??lection ??coles ont ??t?? organis??s par sujet du programme d'??tudes gr??ce aux b??n??voles d'enfants SOS. SOS Enfants a regard?? des enfants en Afrique depuis quarante ans. Pouvez-vous aider dans leur travail en Afrique ?
| Lois de la thermodynamique |
|---|
| Loi Z??ro |
| Premi??re loi |
| Deuxi??me loi |
| Troisi??me loi |
| Relation fondamentale |
Dans la thermodynamique , la premi??re loi de la thermodynamique est une expression de la loi physique plus universelle de la conservation de l'??nergie. Succinctement, la premi??re loi de la thermodynamique:
| " | L'augmentation de l'??nergie interne d'un syst??me est ??gale ?? la quantit?? d'??nergie ajout??e par chauffage du syst??me, moins la quantit?? perdue en raison du travail effectu?? par le syst??me sur son environnement. | " |
Description
La premi??re loi de la thermodynamique stipule essentiellement qu'un syst??me thermodynamique peut stocker ou de conserver l'??nergie et que ce interne de l'??nergie est conserv??e. La chaleur est un processus par lequel l'??nergie est ajout?? ?? un syst??me ?? partir d'une source de haute temp??rature, ou perdu ?? une basse temp??rature ??vier. En outre, l'??nergie peut ??tre perdue par le syst??me quand il fait un travail m??canique sur son environnement, ou ?? l'inverse, il peut gagner de l'??nergie ?? la suite de travaux effectu??s sur elle par son environnement. La premi??re loi stipule que cette ??nergie est conserv??e: La variation de l'??nergie interne est ??gale ?? la quantit?? ajout??e par chauffage moins le montant perdu en faisant des travaux sur l'environnement. La premi??re loi peut ??tre d??clar?? math??matiquement comme:
o??  est une petite augmentation de l'??nergie interne du syst??me,
est une petite augmentation de l'??nergie interne du syst??me, 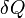 est une petite quantit?? de chaleur ajout??e au syst??me, et
est une petite quantit?? de chaleur ajout??e au syst??me, et  est une petite quantit?? de travail effectu??e par le syst??me. Par analogie, si la chaleur ??tait l'argent, alors nous pourrions dire que tout changement dans nos ??conomies (
est une petite quantit?? de travail effectu??e par le syst??me. Par analogie, si la chaleur ??tait l'argent, alors nous pourrions dire que tout changement dans nos ??conomies (  ) Est ??gale ?? l'argent que nous mettons en (
) Est ??gale ?? l'argent que nous mettons en ( 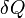 ) Moins l'argent que nous d??pensons (
) Moins l'argent que nous d??pensons ( 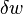 ).
).
Les δ est devant les conditions de chaleur et de travail sont utilis??s pour indiquer qu'ils d??crivent une augmentation de l'??nergie qui doit ??tre interpr??t?? un peu diff??remment que l'incr??ment dU de l'??nergie interne. Travail et chaleur sont des processus qui ajoutent ou soustraient l'??nergie, tandis que le U int??rieur de l'??nergie est une forme particuli??re d'??nergie associ??e avec le syst??me. Ainsi, le terme ????nergie thermique?? pour 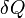 signifie ??cette quantit?? d'??nergie a ajout?? que le r??sultat du chauffage?? plut??t que de se r??f??rer ?? une forme particuli??re d'??nergie. De m??me, le terme "d'??nergie de travail??
signifie ??cette quantit?? d'??nergie a ajout?? que le r??sultat du chauffage?? plut??t que de se r??f??rer ?? une forme particuli??re d'??nergie. De m??me, le terme "d'??nergie de travail?? 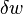 signifie ??cette quantit?? d'??nergie perdue ?? la suite du travail??. Le r??sultat le plus significatif de cette distinction est le fait que l'on peut indiquer clairement la quantit?? d'??nergie interne poss??d?? par un syst??me thermodynamique, mais on ne peut pas dire combien d'??nergie se est ??coul?? dans ou hors du syst??me ?? la suite de son ??tre chauff?? ou refroidi , ni ?? la suite de travaux ex??cut??s sur ou par le syst??me.
signifie ??cette quantit?? d'??nergie perdue ?? la suite du travail??. Le r??sultat le plus significatif de cette distinction est le fait que l'on peut indiquer clairement la quantit?? d'??nergie interne poss??d?? par un syst??me thermodynamique, mais on ne peut pas dire combien d'??nergie se est ??coul?? dans ou hors du syst??me ?? la suite de son ??tre chauff?? ou refroidi , ni ?? la suite de travaux ex??cut??s sur ou par le syst??me.
La premi??re d??claration explicite de la premi??re loi de la thermodynamique a ??t?? donn??e par Rudolf Clausius en 1850 : "Il ya une fonction d'??tat E, appel??e?? ??nergie ??, dont l'??cart est ??gal au travail ??chang?? avec l'environnement au cours d'une processus adiabatique. "
Notez que la formulation ci-dessus est favoris??e par des ing??nieurs et des physiciens. Les chimistes pr??f??rent une seconde forme, dans lequel le terme de travail 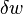 est d??fini comme le travail effectu?? sur le syst??me, et ins??rez donc un signe plus dans l'??quation ci-dessus avant le terme de travail. Cet article va utiliser la premi??re d??finition exclusivement.
est d??fini comme le travail effectu?? sur le syst??me, et ins??rez donc un signe plus dans l'??quation ci-dessus avant le terme de travail. Cet article va utiliser la premi??re d??finition exclusivement.
Formulation math??matique
L'??nonc?? math??matique de la premi??re loi est donn?? par:
o??  est l'augmentation infinit??simale de l'??nergie interne du syst??me,
est l'augmentation infinit??simale de l'??nergie interne du syst??me, 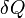 est la quantit?? infinit??simale de chaleur ajout??e au syst??me, et
est la quantit?? infinit??simale de chaleur ajout??e au syst??me, et 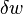 est la quantit?? infinit??simale du travail effectu?? par le syst??me. La chaleur infinit??simal et le travail sont d??sign??s par δ plut??t que d parce que, en termes math??matiques, ils ne sont pas diff??rentielles exactes. En d'autres termes, ils ne d??crivent pas l'??tat de ne importe quel syst??me. L'int??grale d'un diff??rentiel inexacte d??pend du ??chemin?? particuli??re ?? travers l'espace des param??tres thermodynamiques alors l'int??grale d'une diff??rentielle exacte ne d??pend que des ??tats initiaux et finaux. Si les ??tats initiaux et finaux sont les m??mes, alors l'int??grale d'un diff??rentiel inexacte peut ou ne peut pas ??tre nul, mais l'int??grale d'une diff??rentielle exacte sera toujours z??ro. Le chemin emprunt?? par un syst??me thermodynamique dans l'espace d'??tat est connu comme un processus thermodynamique.
est la quantit?? infinit??simale du travail effectu?? par le syst??me. La chaleur infinit??simal et le travail sont d??sign??s par δ plut??t que d parce que, en termes math??matiques, ils ne sont pas diff??rentielles exactes. En d'autres termes, ils ne d??crivent pas l'??tat de ne importe quel syst??me. L'int??grale d'un diff??rentiel inexacte d??pend du ??chemin?? particuli??re ?? travers l'espace des param??tres thermodynamiques alors l'int??grale d'une diff??rentielle exacte ne d??pend que des ??tats initiaux et finaux. Si les ??tats initiaux et finaux sont les m??mes, alors l'int??grale d'un diff??rentiel inexacte peut ou ne peut pas ??tre nul, mais l'int??grale d'une diff??rentielle exacte sera toujours z??ro. Le chemin emprunt?? par un syst??me thermodynamique dans l'espace d'??tat est connu comme un processus thermodynamique.
Une expression de la premi??re loi peut ??tre r??dig??e en termes de diff??rences exactes en r??alisant que le travail que fait un syst??me est ??gale ?? ses moments de pression la variation infinit??simale de son volume. Autrement dit  o??
o?? 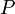 est pression et
est pression et  est le volume . Pour un processus r??versible, la quantit?? totale de chaleur ajout??e ?? un syst??me peut ??tre exprim??e comme
est le volume . Pour un processus r??versible, la quantit?? totale de chaleur ajout??e ?? un syst??me peut ??tre exprim??e comme 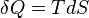 o??
o?? 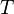 est la temp??rature et
est la temp??rature et  est l'entropie . Pour un processus r??versible, la premi??re loi peut maintenant ??tre reformul??e:
est l'entropie . Pour un processus r??versible, la premi??re loi peut maintenant ??tre reformul??e:
Dans le cas o?? le nombre de particules dans le syst??me ne est pas n??cessairement constante et peut ??tre de diff??rents types, la premi??re loi est d??pos??:
o?? 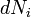 est le (petit) nombre de particules de type i ajout??s au syst??me, et
est le (petit) nombre de particules de type i ajout??s au syst??me, et 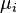 est la quantit?? d'??nergie ajout??e au syst??me quand une particule de type I est ajout??, o?? l'??nergie de cette particule est telle que le volume et l'entropie du syst??me reste inchang??e.
est la quantit?? d'??nergie ajout??e au syst??me quand une particule de type I est ajout??, o?? l'??nergie de cette particule est telle que le volume et l'entropie du syst??me reste inchang??e. 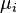 qui est connu comme le le potentiel chimique des particules de type i dans le syst??me. La d??claration de la premi??re loi des processus r??versibles, en utilisant des diff??rentielles exactes est maintenant:
qui est connu comme le le potentiel chimique des particules de type i dans le syst??me. La d??claration de la premi??re loi des processus r??versibles, en utilisant des diff??rentielles exactes est maintenant:
Une id??e de la m??canique utile est que l'??nergie acquise par une particule est ??gale ?? la force appliqu??e ?? la particule multipli?? par le d??placement de la particule pendant que la force est appliqu??e. Consid??rons maintenant la premi??re loi sans le terme de chauffage:  . La pression P peut ??tre consid??r??e comme une force (et en fait a des unit??s de force par unit?? de surface), tandis que dV est le d??placement (avec unit??s de fois la distance r??gion). On peut dire, par rapport ?? cette p??riode de travail, qu'une diff??rence de pression force un transfert de volume et que le produit des deux (travail) est la quantit?? d'??nergie transf??r??e ?? la suite du processus.
. La pression P peut ??tre consid??r??e comme une force (et en fait a des unit??s de force par unit?? de surface), tandis que dV est le d??placement (avec unit??s de fois la distance r??gion). On peut dire, par rapport ?? cette p??riode de travail, qu'une diff??rence de pression force un transfert de volume et que le produit des deux (travail) est la quantit?? d'??nergie transf??r??e ?? la suite du processus.
Il est utile de voir le terme TdS dans la m??me lumi??re: En ce qui concerne ce terme de chaleur, une diff??rence de temp??rature oblige un transfert de l'entropie, et le produit des deux (la chaleur) est la quantit?? d'??nergie transf??r??e ?? la suite du processus . Ici, la temp??rature est connue comme une force "g??n??ralis??" (au lieu d'une force m??canique r??elle) et l'entropie est un d??placement g??n??ralis??.
De m??me, une diff??rence de potentiel chimique entre les groupes de particules dans le syst??me impose une trasfer de particules, et le produit correspondant est la quantit?? d'??nergie transf??r??e ?? la suite du processus. Par exemple, envisager un syst??me compos?? de deux phases: l'eau liquide et la vapeur d'eau. Il existe une "force" g??n??ralis?? qui entra??ne l'??vaporation de mol??cules d'eau hors du liquide. Il ya une ??force?? g??n??ralis??e de la condensation qui entra??ne les mol??cules de vapeur sur la vapeur. Seulement lorsque ces deux ??forces?? (ou potentiels chimiques) sont ??gaux ce qu'il y aura ??quilibre, et le transfert net sera z??ro.
Les deux param??tres thermodynamiques qui forment une paire force-d??placement g??n??ralis?? sont appel??es ??variables conjugu??es". Les deux paires les plus connus sont, bien entendu, la pression-volume et temp??rature-entropie.
Les types de processus thermodynamiques
Chemins ?? travers l'espace des variables thermodynamiques sont souvent sp??cifi??es en maintenant certaines variables thermodynamiques constante. Il est utile de regrouper ces processus en paires, dans lequel chaque variable maintenue constante est un membre d'une paire de conjugu??.
La paire conjugu?? pression-volume est pr??occup?? par le transfert de l'??nergie m??canique ou dynamique ?? la suite des travaux.
- Un processus isobarique se produit ?? une pression constante. Un exemple serait d'avoir un piston mobile dans un cylindre, de sorte que la pression ?? l'int??rieur du cylindre est toujours ?? la pression atmosph??rique, bien qu'il soit isol?? de l'atmosph??re. En d'autres termes, le syst??me est reli?? de fa??on dynamique, par une fronti??re mobile, ?? un r??servoir ?? pression constante.
- Un processus isochore est celui dans lequel le volume est maintenu constant, ce qui signifie que le travail effectu?? par le syst??me sera z??ro. Il se ensuit que, pour la simple syst??me de deux dimensions, toute l'??nergie de la chaleur transf??r??e au syst??me externe sera absorb?? l'??nergie interne. Un processus isochore est ??galement connu comme un processus isom??trique. Un exemple serait de placer une bo??te de conserve ferm??e contenant uniquement de l'air dans un feu. En premi??re approximation, la bo??te ne sera pas ??tendre, et le seul changement sera que le gaz gagne ??nergie interne, comme en t??moigne l'augmentation de sa temp??rature et de pression. Math??matiquement,
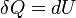 . Nous pouvons dire que le syst??me est dynamique isol??, par une fronti??re rigide, de l'environnement
. Nous pouvons dire que le syst??me est dynamique isol??, par une fronti??re rigide, de l'environnement
La paire conjugu?? temp??rature-entropie est pr??occup?? par le transfert d'??nergie thermique ?? la suite de chauffage.
- Un processus isotherme se produit ?? une temp??rature constante. Un exemple serait d'avoir un syst??me immerg?? dans un grand bain ?? temp??rature constante. Toute l'??nergie de travail effectu??e par le syst??me sera perdu dans le bain, mais sa temp??rature reste constante. En d'autres termes, le syst??me est reli?? thermiquement, par une fronti??re thermiquement conductrice ?? un r??servoir ?? temp??rature constante.
- Un processus isentropique se produit ?? une entropie constante. Pour un processus r??versible ce est identique ?? un processus adiabatique (voir ci-dessous). Si un syst??me a une entropie qui n'a pas encore atteint sa valeur maximale d'??quilibre, un processus de refroidissement peut ??tre n??cessaire pour maintenir cette valeur de l'entropie.
- Un proc??d?? adiabatique est un proc??d?? dans lequel il n'y a pas d'??nergie ajout??e ou soustraite ?? partir du syst??me de chauffage ou de refroidissement. Pour un processus r??versible, ce est identique ?? un processus isentropique. Nous pouvons dire que le syst??me est isol?? thermiquement de son environnement et que sa fronti??re est un isolant thermique. Si un syst??me comporte une entropie qui n'a pas encore atteint sa valeur maximale ?? l'??quilibre, l'entropie augmente m??me si le syst??me est isol?? thermiquement.
Le ci-dessus ont tous assum?? implicitement que les limites sont ??galement imperm??able aux particules. On peut supposer que les fronti??res sont ?? la fois rigide et thermiquement isolant, mais est perm??able ?? un ou plusieurs types de particules. Des consid??rations similaires valent alors pour le (potentiel chimique) - (nombre de particules) des paires conjugu??es.