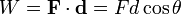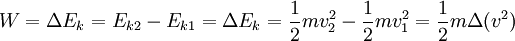Travail (physique)

Sujets connexes: Physique

?? propos de ce ??coles s??lection Wikipedia

Les articles de cette s??lection ??coles ont ??t?? organis??s par sujet du programme d'??tudes gr??ce aux b??n??voles d'enfants SOS. Le parrainage d'enfants aide les enfants un par un http://www.sponsor-a-child.org.uk/ .

En physique , le travail m??canique est la quantit?? de l'??nergie transf??r??e par une vigueur . Comme l'??nergie, ce est un quantit?? scalaire, avec Unit??s SI joules. Le travail ?? long terme a ??t?? invent?? dans les ann??es 1830 par le math??maticien fran??ais Gaspard-Gustave Coriolis.

Selon le th??or??me de l'??nergie si une force ext??rieure agit sur un objet, provoquant sa ??nergie cin??tique pour passer de E ?? E _{k1 k2,} alors le travail m??canique (W) est donn?? par:

$W = \ Delta E_k = E_ {} k2 - E_ {} k1 = \ frac {1} {2} m \ Delta (v ^ 2) \, \!$

o?? m est la masse de l'objet et v est l'objet de vitesse.

Le travail m??canique appliqu??e ?? un objet peut ??tre calcul??e ?? partir de la multiplication scalaire de la appliqu??e vigueur (F) et le d??placement (d) de l'objet. Ce est donn??e par:

$W = \ mathbf {F} \ cdot \ mathbf {d} = Fd \ cos \ theta \, \!$

Introduction

Un baseball pichet fait un travail positif sur la balle en transf??rant l'??nergie en elle. Le Catcher fonctionne n??gative sur elle.

Le travail peut ??tre z??ro, m??me quand il ya une force. Le force centrip??te dans mouvement circulaire, par exemple, fait un travail de z??ro parce que l' ??nergie cin??tique de l'objet mobile ne change pas. De m??me, quand un livre est assis sur une table, la table ne travaille pas sur le livre, car aucune ??nergie ne est transf??r?? dans ou hors de la livre.

conduction de chaleur ne est pas consid??r?? comme une forme de travail, car il n'y a pas de force macroscopiquement mesurables, seules les forces microscopiques qui se produisent dans des collisions atomiques.

Unit??s

L'unit?? SI de travail est le joule (J), qui est d??fini comme le travail effectu?? par une force d'un newton agissant sur une distance d'une m??tre. Cette d??finition est bas??e sur 1824 d??finition de Sadi Carnot de travail comme ??poids soulev?? d'une hauteur", qui est bas??e sur le fait que les moteurs ?? vapeur au d??but ont ??t?? principalement utilis??s pour soulever des seaux d'eau, d'une hauteur de gravitation, de mines de minerai inond??es. L'??quivalent de dimensions newton-m??tre (N ?? m) est parfois utilis?? ?? la place; Cependant, il est ??galement parfois r??serv?? pour des couple de distinguer ses unit??s de travail ou l'??nergie.

Unit??s de travail non-SI sont les erg, le pied-livre, le pieds poundal et le litres atmosph??re.

Calcul math??matique

Force et le d??placement

Force et le d??placement sont les deux vecteurs quantit??s et ils sont combin??s en utilisant la produit scalaire pour ??valuer le travail m??canique, une quantit?? scalaire:

$W = \ gras {F} \ cdot \ gras {d} = F d \ cos \ phi$ (1)

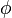o?? $\ Phi$ est l'angle entre la force et le vecteur de d??placement.

Pour que cette formule soit valide, la force et l'angle doit rester constante. Le chemin de l'objet doit toujours rester sur une seule ligne droite, mais il peut changer de direction tout en se d??pla??ant le long de la ligne.

Dans les situations o?? les changements de force plus de temps , ou le chemin se ??carte de la ligne droite, l'??quation (1) ne est g??n??ralement pas applicable m??me se il est possible de diviser le mouvement en petites ??tapes, telle que la force et le mouvement sont bien estim??s comme ??tant constante pour chaque ??tape, puis d'exprimer l'ensemble des travaux que la somme sur ces ??tapes.

La d??finition g??n??rale du travail m??canique est donn??e par la suivante int??grale de ligne:

$W_C: = \ int_ {C} \ gras {F} \ cdot \ mathrm {d} \ gras {s}$ (2)

o??:

C est le chemin ou la courbe parcourue par l'objet;

F est la force de vecteur;

s est la vecteur de position.

L'expression Aw = F ?? d s est un inexact diff??rentiel qui signifie que le calcul de W est _{C-d??pendante} chemin et ne peut pas ??tre diff??renci??e pour donner F ?? d s.

L'??quation (2) explique comment une force non-z??ro peut faire le travail ?? z??ro. Le cas le plus simple est l'endroit o?? la force est toujours perpendiculaire ?? la direction du mouvement, ce qui rend la int??grand toujours z??ro. Ce est ce qui se passe pendant le mouvement circulaire. Cependant, m??me si l'int??grale prend parfois des valeurs non nulles, il peut encore int??grer ?? z??ro se il est parfois n??gatif et parfois positif.

La possibilit?? d'une force non nulle faire le travail ?? z??ro illustre la diff??rence entre le travail et une quantit?? li??e, impulsion, qui est l'int??grale de la force au cours du temps. Mesures Impulse changent dans un corps de l'??lan , une quantit?? de vecteur sensible ?? la direction, tandis que le travail ne consid??re que l'ampleur de la vitesse. Par exemple, comme un objet en mouvement circulaire uniforme traverse la moiti?? d'une r??volution, sa force centrip??te ne travaille pas, mais il transf??re une impulsion non nulle.

??nergie m??canique

L'??nergie m??canique d'un corps est la partie du total de son ??nergie qui est sous r??serve de modifications par le travail m??canique. Il comprend l'??nergie cin??tique et ??nergie potentielle. Certaines formes d'??nergie notables qu'il ne comprend pas sont ??nergie thermique (qui peut ??tre augment??e par travail de frottement, mais pas facilement diminu??) et ??nergie de repos (qui est constant tant que la masse au repos reste le m??me).

Si une force externe F agit sur un corps, provoquant son ??nergie cin??tique pour passer de E ?? E _{k1 k2,} puis:

$W = \ Delta E_k = E_ {} k2 - E_ {} k1 = \ Delta E_k = \ frac {1} {2} mv_2 ^ 2 - \ frac {1} {2} mv_1 ^ 2 = \ frac {1} { 2} m \ Delta (v ^ 2)$

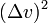Ainsi, nous avons d??riv?? du r??sultat, que le travail m??canique effectu?? par une force externe agissant sur un corps est proportionnelle ?? la diff??rence entre les carr??s des vitesses. (Il est ?? noter que le dernier terme de l'??quation ci-dessus est $\ Delta v ^ 2$ plut??t que $(\ Delta V) ^ 2$ .)

Le principe de conservation de l'??nergie m??canique stipule que, si un syst??me est soumis uniquement ?? forces conservatrices (par exemple uniquement ?? un force gravitationnelle), ou si la somme du travail de toutes les autres forces est nulle, son ??nergie m??canique totale reste constante.

Par exemple, si un objet avec une masse constante est en chute libre, l'??nergie totale de la position 1 sera ??gale ?? celle de la position 2.

$(E_k + E_p) _1 = (E_k + E_p) _2 \, \!$

o??

$E_k$ est l' ??nergie cin??tique , et
$E_p$ est le ??nergie potentielle.

Le travail externe sera g??n??ralement fait par la force de frottement entre le syst??me sur la motion ou de la force interne non-conservatrice dans le syst??me ou perte d'??nergie due ?? la chaleur.

R??cup??r?? ?? partir de " http://en.wikipedia.org/w/index.php?title=Work_(physics)&oldid=230261696 "