
??lan
Renseignements g??n??raux
SOS Enfants, qui se d??roule pr??s de 200 sos ??coles dans le monde en d??veloppement, a organis?? cette s??lection. Parrainage d'enfants aide les enfants du monde en d??veloppement ?? apprendre aussi.
| La m??canique classique |
|---|
|
Branches
|
Formulations M??canique analytique ( ??quations de Lagrange M??canique hamiltonienne) |
Concepts fondamentaux
??nergie
|
Les sujets fondamentaux Corps rigide
La loi de Newton de gravitation universelle
Inertiel / Non-inertielle cadre de r??f??rence
M??canique des planaire mouvement des particules
|
Un mouvement de rotation Mouvement circulaire
Force centrifuge
|

Dans la m??canique classique , l'??lan ( pl. moments; SI unit?? kg ?? m / s, ou, de fa??on ??quivalente, N ?? s) est le produit de la masse et de la vitesse d'un objet (p = mv). Pour des mesures plus pr??cises de l'??lan, consultez la section ??d??finitions modernes de l'??lan" sur cette page. Il est parfois appel?? aussi lin??aire dynamique pour le distinguer du sujet connexe de moment angulaire . La quantit?? de mouvement est un quantit?? de vecteur, car il a une direction et une amplitude. Le moment cin??tique est un quantit?? de pseudovector parce qu'il gagne un signe suppl??mentaire en vertu d'une bascule Antirotation l'impulsion totale d'un groupe d'objets reste le m??me, sauf si des forces ext??rieures agissent sur l'objet.
Momentum est un quantit?? conserv??e, ce qui signifie que l'impulsion totale de tout syst??me ferm?? (un pas affect?? par des forces ext??rieures) ne peut pas changer.
Histoire du concept
Le mot et le concept g??n??ral de l'??lan a ??t?? utilis?? dans le R??publique romaine principalement signifie "un mouvement, le mouvement (comme une force qui l'habite ...)." Un poisson a ??t?? en mesure de changer de vitesse (velocitas) gr??ce ?? l'??lan de sa queue. Le mot est form?? par une accumulation de suffit sur la tige d' latine movere, "?? se d??placer." Un movi-Men est le r??sultat de la movere comme frag-Men est le r??sultat de frangere, "?? briser." Extension par -to- obtient mōvimentum et fragmentum, l'ancien contractant de Momentum.
L'??lan ne ??tait pas simplement la motion, qui ??tait Motus, mais ??tait le pouvoir r??sidant dans un objet en mouvement, captur?? par des d??finitions math??matiques d'aujourd'hui. Un motus, ??mouvement??, a ??t?? une ??tape dans ne importe quel type de changement, tout en velocitas, "rapidit??", captur?? seulement vitesse. Les Romains, en raison des limites inh??rentes au chiffre romain syst??me, ne ont pas pu aller plus loin avec la perception.
L'arriv??e de chiffres arabes dans le 10??me si??cle a ouvert la porte ?? la philosophie quantitative moderne. Le concept de l'??lan en m??canique classique a ??t?? lanc??e par un certain nombre de grands penseurs et des exp??rimentateurs. Le premier d'entre eux ??tait Ibn Sina (Avicenne) circa 1000, qui se est r??f??r?? ?? comme impulsion proportionnelle ?? fois en poids la vitesse . Ren?? Descartes appel??e plus tard fois la masse vitesse que la force fondamentale de mouvement. Galileo dans son Deux nouvelles sciences utilis?? l' italienne mot ??impeto."
La question a ??t?? longuement d??battu de ce que Sir Isaac Newton contribution de l 'au concept ??tait. Apparemment rien, sauf ?? l'??tat plus pleinement et avec de meilleurs outils math??matiques ce qui a ??t?? d??j?? connus. La premi??re et la seconde des Lois du mouvement de Newton avait d??j?? ??t?? ??nonc??e par John Wallis dans son travail 1670, Mechanica sive De Motu, Tractatus geometricus: "l'??tat initial du corps, soit de repos ou de mouvement, vont persister" et "Si la force est sup??rieure ?? la r??sistance, le mouvement se traduira ... . "Wallis utilise ??lan et vis pour la force.
Newton "Principes math??matiques de la Natural History" quand le premier est sorti en 1686 a montr?? un casting similaire autour des mots ?? utiliser pour l'??lan math??matique. Ses d??finit D??finition II quantitas motus, ??quantit?? de mouvement??, comme ??d??coulant de la vitesse et la quantit?? de la mati??re conjointement", qui l'identifie comme l'??lan. Ainsi, quand en droit II, il se r??f??re ?? mutatio motus, "changement de mouvement," ??tant proportionnelle ?? la force impressionn??, il est g??n??ralement pris pour signifier ??lan et pas le mouvement.
Il ne restait plus qu'?? attribuer un terme standard pour la quantit?? de mouvement. La premi??re utilisation de ??momentum?? dans son sens math??matique appropri??e ne est pas clair, mais au moment de Miscellan??es de Jenning en 1721, quatre ans avant la derni??re ??dition de Principia Mathematica de Newton, l'??lan M ou ??quantit?? de mouvement?? ??tait d??fini pour les ??tudiants que "un rectangle", le produit de V et Q, o?? Q est "quantit?? de mati??re" et V est "vitesse", s / t.
La quantit?? de mouvement d'une particule

Si un objet se d??place dans toute trame de r??f??rence, puis elle a impulsion dans ce cadre. Il est important de noter que la quantit?? de mouvement est encadrer d??pendante. Cela signifie que le m??me objet peut avoir une certaine impulsion dans une trame de r??f??rence, mais une quantit?? diff??rente dans un autre cadre. Par exemple, un objet en mouvement a lanc??e dans un cadre de r??f??rence fix?? ?? un point sur le sol, tout en ayant en m??me temps 0 dynamique dans un cadre de r??f??rence fix?? ?? l'objet de centre de masse .
La quantit?? de mouvement d'un objet qui a d??pend de deux grandeurs physiques: la masse et la vitesse de l'objet mobile dans la cadre de r??ference. En physique, le symbole usuel de l'??lan est un petit p gras (gras, car il est un vecteur ); si cela peut se ??crire:
o??:
 est l'??lan
est l'??lan 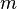 est la masse
est la masse  la vitesse
la vitesse
Exemple: un avion de mod??le de 1 kg voyageant vers le nord ?? 1 m / s en vol rectiligne et le niveau a un ??lan de 1 kg m / s plein nord ?? partir du sol. Pour le pilote factice dans le cockpit, il a une vitesse et l'??lan de z??ro.
Selon la seconde loi de Newton le taux de variation de l'impulsion d'une particule est proportionnelle ?? la force r??sultante agissant sur la particule et est dans la direction de cette force. Dans le cas d'une masse constante, et des vitesses beaucoup moins que la vitesse de la lumi??re, cette d??finition r??sultats dans l'??quation
ou tout simplement
o?? F est comprise comme ??tant la r??sultante .
Exemple: un avion de mod??le de 1 kg acc??l??re de repos ?? une vitesse de 1 m / sec, nord, 1 sec. La pouss??e n??cessaire pour produire cette acc??l??ration est une newton. Le changement de momentum est un kg-m / sec. Pour le pilote factice dans le cockpit il n'y a pas de changement de vitesse. Son appuyant sur le si??ge arri??re est une r??action ?? la pouss??e asym??trique, peu ??tre pond??r??es par la tra??n??e.
La quantit?? de mouvement d'un syst??me de particules
Relative ?? la masse et de la vitesse
La quantit?? de mouvement d'un syst??me de particules est la somme vectorielle des impulsions de tous les objets individuels dans le syst??me.
o??
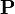 est la dynamique du syst??me de particules
est la dynamique du syst??me de particules 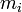 est la masse de l'objet i
est la masse de l'objet i  la vitesse de vecteur de l'objet i
la vitesse de vecteur de l'objet i 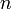 est le nombre d'objets dans le syst??me
est le nombre d'objets dans le syst??me
On peut montrer que, dans le centre de masse de l'??lan d'un syst??me est nulle. En outre, la dynamique dans un cadre de r??f??rence qui se d??place ?? une vitesse 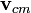 par rapport ?? cette trame est simplement:
par rapport ?? cette trame est simplement:
o??:
 .
.
Relative ?? motoventil?? ??quations g??n??rales du mouvement

La quantit?? de mouvement d'un syst??me de particules peut ??galement ??tre d??fini comme le produit de la masse totale 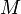 le syst??me de fois la vitesse du centre de masse
le syst??me de fois la vitesse du centre de masse 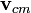
Ceci est commun??ment connu comme seconde loi de Newton .
Pour une d??rivation plus g??n??rale en utilisant tenseurs, nous consid??rons un corps mobile (voir la figure), suppos?? comme un continuum, occupant un volume  ?? la fois
?? la fois 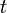 , Ayant une aire de surface
, Ayant une aire de surface 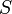 , Avec les forces de traction ou de surface d??finies
, Avec les forces de traction ou de surface d??finies  agissant sur tous les points de la surface du corps, les forces du corps
agissant sur tous les points de la surface du corps, les forces du corps  par unit?? de volume ?? chaque point dans le volume
par unit?? de volume ?? chaque point dans le volume  Et un champ de vitesse
Et un champ de vitesse  pr??vue dans le corps. ?? la suite de l'??quation pr??c??dente, la quantit?? de mouvement du syst??me est la suivante:
pr??vue dans le corps. ?? la suite de l'??quation pr??c??dente, la quantit?? de mouvement du syst??me est la suivante:
Par d??finition, le vecteur de stress est  , Puis
, Puis
En utilisant le Divergence th??or??me de Gauss pour convertir une surface int??grante d'une partie int??grante de volume donne
Pour un volume arbitraire l'int??grale dispara??t, et nous avons les ??quations de Cauchy du mouvement
Si un syst??me est en ??quilibre, la variation de quantit?? de mouvement par rapport au temps est ??gal ?? 0, car il n'y a pas d'acc??l??ration.
ou en utilisant des tenseurs,
Ce sont les ??quations d'??quilibre qui sont utilis??s dans m??canique des solides pour r??soudre les probl??mes de ??lasticit?? lin??aire. Dans la notation d'ing??nierie, les ??quations d'??quilibre sont exprim??s en
Conservation de la quantit?? de mouvement
La loi de conservation de quantit?? de mouvement est une loi fondamentale de la nature, et il affirme que l'impulsion totale d'un syst??me ferm?? d'objets (qui n'a pas d'interactions avec les agents ext??rieurs) est constante. Une des cons??quences de ceci est que le centre de masse de toute Syst??me selon la objets seront toujours continuer ?? la m??me vitesse, ?? moins sollicit?? par une force de l'ext??rieur du syst??me.
Conservation du moment est une cons??quence math??matique de la homog??n??it?? (changement sym??trie ) de l'espace (position dans l'espace est le la quantit?? de conjugu?? canonique dynamique). Donc, conservation de l'impulsion peut ??tre philosophiquement a d??clar?? que ??rien ne d??pend de l'emplacement en soi".
Dans un syst??me isol?? (une o?? les forces externes sont absents) l'impulsion totale sera constante: ce est impliqu??e par Newton premi??re loi du mouvement. Troisi??me loi du mouvement de Newton, le droit des actions r??ciproques , qui veut que les forces agissant entre les syst??mes sont de grandeur ??gale, mais de signe oppos??, est due ?? la conservation de l'impulsion.
Depuis position dans l'espace est une grandeur vectorielle, l'??lan (soit le conjugu?? canonique de la position) est une grandeur vectorielle ainsi - il a la direction. Ainsi, lorsqu'un pistolet est tir??, la quantit?? de mouvement totale finale du syst??me (le pistolet et la balle) est la somme vectorielle des quantit??s de mouvement de ces deux objets. En supposant que le pistolet et balle ??taient au repos avant de tirer (ce qui signifie l'??lan initial du syst??me ??tait de z??ro), l'impulsion totale finale doit aussi ??gal ?? 0.
Dans un syst??me isol?? avec seulement deux objets, le changement dans la dynamique d'un objet doit ??tre ??gale et oppos??e ?? la modification dynamique de l'autre objet. Math??matiquement,
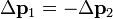
Momentum a la propri??t?? sp??ciale qui, dans un syst??me de fermeture, il est toujours conserv??e, m??me en les collisions et les s??parations caus??es par les forces explosives. L'??nergie cin??tique , d'autre part, ne est pas conserv??e dans des collisions se ils ne sont pas ??lastiques. Depuis dynamique est conserv?? il peut ??tre utilis?? pour calculer une vitesse inconnue apr??s une collision ou une s??paration si toutes les autres masses et les vitesses sont connues.
Un probl??me commun dans la physique qui n??cessite l'utilisation de ce fait est la collision de deux particules. Depuis l'??lan est toujours conserv??e, la somme des moments avant la collision doit ??tre ??gale ?? la somme des moments apr??s la collision:
o??:
- u signifie vecteur vitesse avant la collision
- v signifie vecteur vitesse apr??s la collision.
Habituellement, nous ne savons ni les vitesses avant ou apr??s une collision et nous aimerions aussi savoir le contraire. Correctement r??soudre ce probl??me signifie que vous devez savoir quel type de collision a eu lieu. Il ya deux types de base de collisions, qui tous deux conserver le moment:
- Collisions ??lastiques conserver l'??nergie cin??tique ainsi que quantit?? de mouvement totale avant et apr??s la collision.
- Collisions in??lastiques ne conserver l'??nergie cin??tique, mais quantit?? de mouvement totale avant et apr??s la collision est conserv??e.
Collisions ??lastiques
Une collision entre deux boules de billard est un bon exemple d'une collision presque totalement ??lastique. En plus de l'??lan ??tant conserv?? lorsque les deux balles se entrechoquent, la somme de l'??nergie cin??tique avant une collision doit ??tre ??gale ?? la somme de l'??nergie cin??tique apr??s:
Depuis le facteur 1/2 est commun ?? tous les termes, il peut ??tre pris tout de suite.
Collision frontale (une dimension)
Dans le cas de deux objets en collision t??te, nous constatons que la vitesse finale
qui peut alors facilement ??tre reconstitu??es ??
Cas particulier: m 1 m 2 >>
Consid??rons maintenant le cas o?? la masse d'un corps, par exemple 1 m, est beaucoup plus grande que celle de l'autre, m 2 (m 1 m 2 >>). Dans ce cas m 1 + m 2 est approximativement ??gal ?? m 1 et m 1 -m 2 est approximativement ??gale ?? 1 m.
L'utilisation de ces approximations, la formule ci-dessus pour  r??duit ??
r??duit ??  . Son interpr??tation physique est que dans le cas d'une collision entre deux corps, dont l'un est beaucoup plus massive que l'autre, le corps d'allumage finit par se d??placer dans la direction oppos??e par deux fois la vitesse initiale du corps plus massif.
. Son interpr??tation physique est que dans le cas d'une collision entre deux corps, dont l'un est beaucoup plus massive que l'autre, le corps d'allumage finit par se d??placer dans la direction oppos??e par deux fois la vitesse initiale du corps plus massif.
Cas particulier: m 1 = m 2
Un autre cas particulier est lorsque la collision est entre deux corps de masse ??gale.
Dites m1 de corps en mouvement ?? la vitesse v 1 gr??ves corps m 2 est au repos (v 2). Mettre ce cas dans l'??quation d??riv??e ci-dessus, nous allons voir que, apr??s la collision, le corps qui se d??pla??ait (m 1) commencera ?? se d??placer ?? la vitesse v 2 et la masse m 2 va commencer ?? se d??placer avec une vitesse v 1. Donc, il y aura un ??change de vitesses.
Supposons maintenant que l'une des masses, dit m 2, ??tait au repos. Dans ce cas, apr??s la collision du corps en mouvement, m 1, viendra le repos et le corps qui ??tait au repos, m 2, commencera ?? se d??placer ?? la vitesse que M 1 avait avant la collision.
Notez que toutes ces observations sont d'une collision ??lastique.
Ce ph??nom??ne se manifeste par Le berceau de Newton, l'un des exemples les plus connus de la conservation du moment, un exemple concret de ce cas particulier.
Collisions multi-dimensionnelles
Dans le cas d'objets qui entrent en collision dans plus d'une dimension, comme dans les collisions obliques, la vitesse est r??solu en des composantes orthogonales avec une composante perpendiculaire au plan de collision et l'autre composant ou des composants dans le plan de collision. Les composantes de vitesse dans le plan de collision restent inchang??es, tandis que la vitesse perpendiculaire au plan de collision est calcul??e de la m??me mani??re que le cas unidimensionnel.
Par exemple, en cas de collision ?? deux dimensions, les quantit??s de mouvement peut ??tre d??compos??e en composantes x et y. On peut alors calculer chaque composant s??par??ment, et de les combiner pour produire un r??sultat de vecteur. L'ampleur de ce vecteur est l'??lan final du syst??me isol??.
Voir la page collision ??lastique pour plus de d??tails. 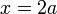
Collisions in??lastiques
Un exemple courant d'une collision parfaitement in??lastique, ce est quand deux boules de neige en collision puis collent ensemble par la suite. Cette ??quation d??crit la conservation du moment:
On peut montrer qu'une collision parfaitement in??lastique est celui dans lequel le montant maximal de l'??nergie cin??tique est convertie en d'autres formes. Par exemple, si les deux objets collent ensemble apr??s la collision et se d??placent avec une vitesse finale commune, on peut toujours trouver un cadre de r??f??rence dans lequel les objets sont mis au repos par la collision et 100% de l'??nergie cin??tique est convertie. Cela est vrai m??me dans le cas relativiste et utilis??es dans acc??l??rateurs de particules pour convertir efficacement l'??nergie cin??tique en de nouvelles formes de masse-??nergie (ce est ?? dire pour cr??er des particules massives).
En cas de collision in??lastique, il ya un param??tre attach?? appel?? coefficient de restitution (not??e minuscule ??e?? ou ??c?? dans de nombreux livres de texte). Il est d??fini comme le rapport de vitesse relative de s??paration ?? une vitesse relative d'approche. Ce est un rapport o?? il est une grandeur sans dimension.
Quand on a une collision ??lastique la valeur de e (= coefficient de restitution) est 1, ce est ?? dire la vitesse relative d'approche est ??gale ?? la vitesse relative de s??paration des corps en collision. Dans une collision ??lastique l'??nergie cin??tique du syst??me est conserv??e.
Lorsqu'une collision est pas ??lastique (e <1), il se agit d'une collision ??lastique. Dans le cas d'une collision parfaitement in??lastique de la vitesse relative de s??paration du centre de masse du corps en collision est 0. Par cons??quent, apr??s collision organes coller ensemble apr??s collision. Dans le cas d'une collision in??lastique la perte d'??nergie cin??tique est maximale comme indiqu?? ci-dessus.
Dans tous les types de collision si aucune force ext??rieure ne agit sur le syst??me des organes collision, l'??lan obtiendrez toujours pr??serv??.
Explosions
Une explosion se produit lorsqu'un objet est divis?? en deux ou plusieurs fragments en raison d'une lib??ration d'??nergie. Notez que l'??nergie cin??tique d'un syst??me d'explosion ne est pas conserv??e car elle implique la transformation d'??nergie. (ce est ?? dire des changements de l'??nergie cin??tique en ??nergie thermique et sonore)
http://www.glenbrook.k12.il.us/gbssci/phys/Class/momentum/u4l2e.html
Dans le canon d??monstration explosion, la dynamique du syst??me totale est conserv??e. Le syst??me se compose de deux objets - un canon et une balle de tennis. Avant l'explosion, l'impulsion totale du syst??me est nul car le canon et la balle de tennis situ?? ?? l'int??rieur de celui-ci sont ?? la fois au repos. Apr??s l'explosion, la quantit?? de mouvement totale de l'installation doit toujours ??tre ??gal ?? z??ro. Si la balle acquiert 50 unit??s de l'??lan avant, puis le canon acquiert 50 unit??s de l'arri??re ??lan. La somme vectorielle des quantit??s de mouvement individuel des deux objets est 0. dynamique totale du syst??me est conserv??e.
Voir la la page de collision in??lastique pour plus de d??tails.
Les d??finitions modernes de l'??lan
Momentum en m??canique relativiste
Dans la m??canique relativiste, pour ??tre conserv??, l'??lan doit ??tre d??fini comme:
o??
 est le masse invariante de l'objet mobile,
est le masse invariante de l'objet mobile, 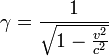 est le Facteur de Lorentz
est le Facteur de Lorentz 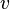 est la vitesse relative entre un objet et un observateur
est la vitesse relative entre un objet et un observateur  est la vitesse de la lumi??re .
est la vitesse de la lumi??re .
Dynamique relativiste peut ??galement ??tre ??crit comme temps de masse invariante de l'objet la vitesse appropri??e, d??fini comme le taux de changement de position de l'objet dans le cadre d'observateur par rapport au temps ??coul?? sur les horloges de l'objet (c.-??-objet bon moment). Dynamique relativiste devient dynamique newtonienne:  ?? basse vitesse
?? basse vitesse  .
.
Relativiste quatre dynamique propos??e par Albert Einstein d??coule de l'invariance de -quatre vecteurs sous la traduction de Lorentz. Les quatre-dynamique est d??finie comme:
o??
 est le
est le 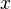 composante de la dynamique relativiste,
composante de la dynamique relativiste, 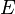 est l'??nergie totale du syst??me:
est l'??nergie totale du syst??me: 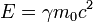
La "longueur" du vecteur est la masse multipli??e par la vitesse de la lumi??re, qui est invariante pour toutes les trames de r??f??rence:
Momentum d'objets sans masse
Objets sans masse au repos, comme les photons , portent aussi dynamique. La formule est la suivante:
o??
 est La constante de Planck,
est La constante de Planck,  est le longueur d'onde du photon,
est le longueur d'onde du photon, 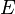 est l' ??nergie du photon et porte
est l' ??nergie du photon et porte  est la vitesse de la lumi??re .
est la vitesse de la lumi??re .
G??n??ralisation de l'??lan
Momentum est le Noether responsable de l'invariance de translation. Ainsi, m??me les champs ainsi que d'autres choses peuvent avoir l'??lan, pas de particules juste. Cependant, espace-temps courbe qui ne est pas asymptotiquement Minkowski, l'??lan ne est pas d??fini du tout.
Momentum en m??canique quantique
En m??canique quantique , l'??lan est d??finie comme une op??rateur sur la fonction d'onde. Le Heisenberg principe d'incertitude d??finit les limites de la pr??cision de l'??lan et de la position d'un syst??me unique observables peuvent ??tre connus ?? la fois. En m??canique quantique, la position et l'??lan sont les variables conjugu??.
Pour une seule particule sans charge ??lectrique et aucune rotation, l'op??rateur de l'??lan peut ??tre ??crit dans la base de position
o??:
 est le op??rateur gradient;
est le op??rateur gradient;  est le r??duit la constante de Planck;
est le r??duit la constante de Planck;  est l' unit?? imaginaire .
est l' unit?? imaginaire .
Ce est une forme couramment rencontr?? de l'op??rateur de l'??lan, mais pas la plus g??n??rale.
Momentum en ??lectromagn??tisme
Les champs ??lectriques et magn??tiques poss??dent dynamique ind??pendamment du fait qu'ils sont statiques ou ils changent dans le temps. Ce est une grande surprise pour ??tudiants de premi??re ann??e qui sont introduits dans le fait bien connu de la pression  d'un ??lectrostatique (magn??tostatique) champ sur une sph??re de m??tal, la capacit?? cylindrique ou barreau ferromagn??tique:
d'un ??lectrostatique (magn??tostatique) champ sur une sph??re de m??tal, la capacit?? cylindrique ou barreau ferromagn??tique:
o??  ,
, 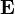 ,
, 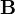 , Sont la densit?? d'??nergie ??lectromagn??tique, champs ??lectriques et magn??tiques respectivement. La pression ??lectromagn??tique
, Sont la densit?? d'??nergie ??lectromagn??tique, champs ??lectriques et magn??tiques respectivement. La pression ??lectromagn??tique 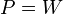 peut ??tre suffisamment ??lev??e pour la capacit?? d'exploser. Ainsi, les champs ??lectriques et magn??tiques ne portent ??lan.
peut ??tre suffisamment ??lev??e pour la capacit?? d'exploser. Ainsi, les champs ??lectriques et magn??tiques ne portent ??lan.
Lumi??re (visible, UV, radio) est une onde ??lectromagn??tique et a aussi dynamique. M??me si photons (aspect corpusculaire de la lumi??re) ne ont pas de masse, ils portent encore tr??s dynamique. Cela conduit ?? des applications telles que la voile solaire.
Momentum est conserv??e dans un syst??me ??lectrodynamique (il peut changer d'une dynamique dans les domaines de la dynamique m??canique de pi??ces mobiles). Le traitement de la dynamique d'un champ est habituellement r??alis?? en consid??rant que l'on appelle tenseur impulsion-??nergie et le changement dans le temps de la Vecteur de Poynting int??gr??e sur un peu de volume. Ce est un champ tensoriel qui a des composantes li??es ?? la densit?? d'??nergie et la densit?? de quantit?? de mouvement.
La d??finition canonique dynamique correspondant ?? l'op??rateur de quantit?? de mouvement de la m??canique quantique quand il interagit avec le champ ??lectromagn??tique est, en utilisant la principe de couplage moins:
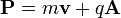 ,
,
au lieu de la coutumier
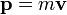 ,
,
o??:
 est le potentiel vecteur ??lectromagn??tique
est le potentiel vecteur ??lectromagn??tique 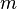 masse invariante de la particule charg??e
masse invariante de la particule charg??e 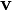 sa vitesse
sa vitesse 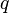 sa charge.
sa charge.

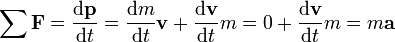





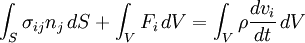


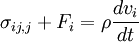





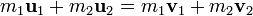




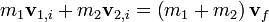
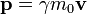

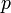 . Se il vous pla??t noter que dans la notation utilis??e par le cr??ateur de la figure, la masse invariante
. Se il vous pla??t noter que dans la notation utilis??e par le cr??ateur de la figure, la masse invariante  est index??e par un z??ro,
est index??e par un z??ro, 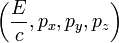



![P_ {static} = {} W = [{\ epsilon_0 \ epsilon} {\ frac {{\ mathbf E} ^ 2} {{2}}} + {\ frac {1} {{\ mu_0 \ mu}}} {\ frac {{\ mathbf B} ^ 2} {{2}}}],](../../images/160/16078.png)
