
Vitesse de la lumi??re
Saviez-vous ...
Cette s??lection ??coles a ??t?? choisi par SOS Enfants pour les ??coles dans le monde en d??veloppement ne ont pas acc??s ?? Internet. Il est disponible en t??l??chargement intranet. SOS Enfants a regard?? des enfants en Afrique depuis quarante ans. Pouvez-vous aider dans leur travail en Afrique ?
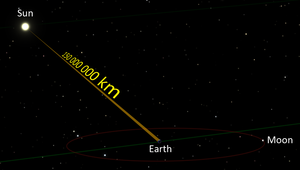 Sunlight prend environ 8 minutes 19 secondes pour atteindre la Terre (sur la base de la distance moyenne). | |
| Les valeurs exactes | |
|---|---|
| M??tres par seconde | 299792458 |
| Unit??s de Planck | 1 |
| kilom??tres par seconde | 299,792.458 |
| Approximatives | |
| kilom??tres par heure | 1080 millions |
| miles par seconde | 186000 |
| miles par heure | 671000000 |
| unit??s astronomiques par jour | 173 |
| Temps de trajet du signal lumineux approximatif | |
| Distance | Temps |
| une pied | 1.0 ns |
| une m??tre | 3,3 ns |
| ?? partir de orbite g??ostationnaire ?? la Terre | 119 mlle |
| la longueur de la Terre de l'??quateur | 134 ms |
| de la Lune ?? la Terre | 1.3 s |
| de Sun ?? la Terre (une UA) | 8.3 min |
| d' ??toile la plus proche ?? Sun (1,3 pc) | 4,2 ann??es |
| de la galaxie la plus proche (la Canis Major de galaxie naine) sur Terre | 25000 ann??es |
| ?? travers la Voie Lact??e | 100000 ann??es |
| de la galaxie d'Androm??de ?? la Terre | 2.500.000 ann??es |
La vitesse de la lumi??re dans vide, c couramment not??e, est un universel constante physique important dans de nombreux domaines de la physique . Sa valeur est 299792458 m??tres par seconde, ce qui est un chiffre exact car la longueur de l'appareil de mesure est d??fini ?? partir de cette constante et la norme internationale pour le temps. En unit??s imp??riales cette vitesse est d'environ 186,282 miles par seconde. Selon la relativit?? restreinte , c est la vitesse maximale ?? laquelle toute l'??nergie, la mati??re et informations dans le univers peut voyager. Ce est la vitesse ?? laquelle toutes particules sans masse et associ?? domaines (y compris le rayonnement ??lectromagn??tique , comme la lumi??re ) voyagent dans le vide. Ce est aussi le vitesse de gravit?? (par exemple de ondes gravitationnelles) pr??dites par les th??ories actuelles. Ces particules et des ondes se d??placent ?? c quel que soit le mouvement de la source ou de la rep??re inertiel de l'observateur. Dans la th??orie de la relativit?? , c interrelie espace et le temps, et apparaissent ??galement dans la c??l??bre ??quation d' l'??quivalence masse-??nergie E = mc 2.
La vitesse ?? laquelle la lumi??re se propage ?? travers mat??riaux transparents tels que le verre ou l'air, est inf??rieure ?? c. Le rapport entre c et la vitesse v ?? laquelle la lumi??re se propage dans un mat??riau est appel?? le indice de r??fraction n du mat??riau (n = c / v). Par exemple, pour la lumi??re visible l'indice de r??fraction du verre est g??n??ralement autour de 1,5, ce qui signifie que la lumi??re dans le verre se d??place ?? c / 1,5 ≈ 200000 km / s; l' indice de r??fraction de l'air pour la lumi??re visible est d'environ 1,0003, de sorte que la vitesse de la lumi??re dans l'air est d'environ 90 km / s plus lent que c.
Dans les cas les plus pratiques, la lumi??re peut ??tre consid??r?? comme mobile "instantan??ment", mais pour les longues distances et des mesures tr??s sensibles de la vitesse finie de la lumi??re a des effets notables. Par exemple, dans les vid??os d'un orage intense sur la surface de la Terre prises depuis la Station spatiale internationale, l'expansion de fronts d'onde lumi??re provenant de bouff??es individuelles de la foudre est clairement visible, et permet des estimations de la vitesse de la lumi??re ?? ??tre fabriqu??s ?? partir trame ?? -frame analyse de la position du front d'onde de la lumi??re. Ce ne est pas surprenant, ??tant donn?? le temps pour que la lumi??re se propage tout autour de la Terre est de l'ordre de 140 millisecondes. Ce temps de transit est ce qui provoque la R??sonance de Schumann. En communiquant avec lointaine sondes spatiales, il peut prendre quelques minutes ?? quelques heures d'un message pour obtenir de la Terre ?? l'engin spatial, ou vice versa. La lumi??re que nous voyons des ??toiles les a quitt?? il ya de nombreuses ann??es, ce qui nous permet d'??tudier l'histoire de l'univers en regardant les objets ??loign??s. La vitesse finie de la lumi??re limite ??galement la vitesse maximale th??orique de l'informatique , puisque l'information doit ??tre envoy?? dans l'ordinateur de puce ?? puce. Enfin, la vitesse de la lumi??re peut ??tre utilis?? avec temps des mesures de vol pour mesurer de grandes distances ?? haute pr??cision.
Ole R??mer abord d??montr?? en 1676 que la lumi??re voyage ?? une vitesse finie (par opposition ?? instantan??ment) en ??tudiant le mouvement apparent de Jupiter moon s ' Io. En 1865, James Clerk Maxwell a propos?? que la lumi??re ??tait une onde ??lectromagn??tique, et donc voyag?? ?? la vitesse c apparaissant dans sa th??orie de l'??lectromagn??tisme. En 1905, Albert Einstein a postul?? que la vitesse de la lumi??re par rapport ?? ne importe quel r??f??rentiel inertiel est ind??pendante du mouvement de la source lumineuse, et a explor?? les cons??quences de ce postulat en d??rivant la th??orie de la relativit?? et de montrer que le param??tre c ??tait pertinente l'ext??rieur le contexte de la lumi??re et de l'??lectromagn??tisme. Apr??s des si??cles de mesures de plus en plus pr??cises, en 1975 la vitesse de la lumi??re a ??t?? connu pour ??tre 299 792 458 m / s avec un l'incertitude de mesure de 4 parties par milliard. En 1983, le m??tre a ??t?? red??fini dans le Syst??me international d'unit??s (SI) comme la distance parcourue par la lumi??re dans le vide en 1 / 299.792.458 d'un secondes. En cons??quence, la valeur num??rique de c en m??tres par seconde est corrig?? de fa??on pr??cise par la d??finition du m??tre.
Valeur num??rique, la notation, et des unit??s
La vitesse de la lumi??re dans le vide est not??e c. Le symbole c est un "c onstant" dans physique syst??mes d'unit??s, et c est ??galement synonyme de " celeritas ", latin pour" la rapidit?? ". (Capital C est la Unit?? SI coulomb de charge ??lectrique .) ?? l'origine, le symbole V a ??t?? utilis?? pour la vitesse de la lumi??re, introduite par James Clerk Maxwell en 1865. En 1856, Wilhelm Eduard Weber et Rudolf Kohlrausch avait utilis?? c pour une constante diff??rente montr?? plus tard pour ??galer √ 2 fois la vitesse de la lumi??re dans le vide. En 1894, Paul Drude red??fini c avec son sens moderne. Einstein utilis?? V dans son originaux, des documents en langue allemande sur la relativit?? restreinte en 1905, mais en 1907 il est pass?? ?? c, qui avait alors devenu le symbole standard.
Parfois, c est utilis??e pour la vitesse des ondes sur tout support mat??riel, et c 0 de la vitesse de la lumi??re dans le vide. Cette notation indic??e, qui est approuv?? dans la litt??rature officielle de SI, a la m??me forme que les autres constantes connexes: ?? savoir, μ 0 pour le perm??abilit?? du vide ou de la constante magn??tique, ε 0 pour le permittivit?? du vide ou la constante ??lectrique, et Z 0 pour la imp??dance de l'espace libre. Cet article utilise exclusivement pour c la vitesse de la lumi??re dans le vide.
Dans le Syst??me international d'unit??s (SI), le compteur est d??fini comme la distance parcourue par la lumi??re dans le vide en 1/299 792 458 de seconde. Cette d??finition fixe la vitesse de la lumi??re dans le vide ?? exactement 299 792 458 m / s. Comme un dimensionnelle constante physique, la valeur num??rique de c est diff??rente pour diff??rents syst??mes d'unit??s. Dans branches de la physique dans lequel c appara??t souvent, comme en relativit??, il est courant d'utiliser des syst??mes de unit??s naturelles ou de la mesure Syst??me d'unit??s g??om??triques o?? c = 1. L'utilisation de ces unit??s, c ne appara??t pas explicitement car la multiplication ou division par 1 ne affecte pas le r??sultat.
R??le fondamental en physique
La vitesse ?? laquelle les ondes lumineuses se propagent dans le vide est ind??pendante ?? la fois du mouvement de la source d'onde et de la rep??re inertiel de l'observateur. Cette invariance de la vitesse de la lumi??re a ??t?? postul?? par Einstein en 1905, apr??s avoir ??t?? motiv??e par la th??orie de Maxwell de l'??lectromagn??tisme et l'absence de preuve de l' ??ther luminif??re ; il a depuis ??t?? constamment confirm?? par de nombreuses exp??riences. Il est seulement possible de v??rifier exp??rimentalement que la vitesse dans les deux sens de la lumi??re (par exemple, ?? partir d'une source et un miroir de retour) est ind??pendante de trame, car il est impossible de mesurer la Vitesse de la lumi??re dans un seul sens (par exemple, provenant d'une source ?? un d??tecteur ?? distance) sans une convention sur la mani??re dont les horloges ?? la source et au d??tecteur doivent ??tre synchronis??s. Cependant, en adoptant Einstein pour la synchronisation des horloges, la vitesse d'un chemin de lumi??re devient ??gale ?? la vitesse dans les deux sens de la lumi??re par d??finition. La th??orie de la relativit?? explore les cons??quences de cette invariance de c avec l'hypoth??se que les lois de la physique sont les m??mes dans tous les r??f??rentiels inertiels. Une cons??quence est que c est la vitesse ?? laquelle toutes particules et des ondes sans masse, y compris la lumi??re, doivent voyager dans le vide.

La relativit?? sp??ciale a de nombreuses implications contre-intuitifs et v??rifi??s exp??rimentalement. Ceux-ci comprennent le ??quivalence de la masse et de l'??nergie (E = mc 2), la contraction des longueurs (objets en mouvement raccourcir), et dilatation du temps (horloges mobiles ex??cutent plus lentement). La γ de facteur par lequel longueurs contrat et parfois dilater est connu sous le nom Facteur de Lorentz et est donn??e par γ = (1 - v 2 / c 2) -1/2, o?? v est la vitesse de l'objet. La diff??rence de γ de 1 est n??gligeable pour des vitesses beaucoup plus lent que c, comme la plupart des vitesses dans la vie quotidienne auquel cas la relativit?? restreinte est ??troitement approch??e par Relativit?? galil??enne, mais elle augmente ?? des vitesses relativistes et diverge ?? l'infini comme v approche c.
Les r??sultats de la relativit?? restreinte peuvent ??tre r??sum??es en traitant l'espace et le temps comme une structure unifi??e connu sous le nom l'espace-temps (avec c concernant les unit??s de temps et l'espace), et en exigeant que les th??ories physiques satisfaire une sp??ciale sym??trie appel?? Invariance de Lorentz, dont la formulation math??matique contient le param??tre c. Invariance de Lorentz est une hypoth??se presque universelle pour les th??ories physiques modernes, tels que ??lectrodynamique quantique, chromodynamique quantique, le mod??le standard de la physique des particules , et la relativit?? g??n??rale . En tant que tel, le param??tre c est omnipr??sent dans la physique moderne, apparaissant dans de nombreux contextes qui ne sont pas li??s ?? la lumi??re. Par exemple, la relativit?? g??n??rale pr??dit que c est aussi le vitesse de la gravit?? et de ondes gravitationnelles. En cadres non-inertiels de r??f??rence (l'espace courbe ou gravitationnellement acc??l??r??e des cadres de r??f??rence), la vitesse locale de la lumi??re est constante et ??gale ?? c, mais le vitesse de la lumi??re le long d'une trajectoire de longueur finie peuvent diff??rer c, en fonction de la distance et du temps sont d??finis.
Il est g??n??ralement suppos?? que constantes fondamentales telles que c ont la m??me valeur ?? travers l'espace-temps, ce qui signifie qu'ils ne d??pendent pas de l'emplacement et ne varient pas avec le temps. Cependant, il a ??t?? propos?? dans diverses th??ories qui la vitesse de la lumi??re peut avoir chang?? au fil du temps. Aucune preuve concluante de tels changements a ??t?? trouv??, mais ils restent l'objet de recherches en cours.
Il est ??galement g??n??ralement admis que la vitesse de la lumi??re est isotrope, ce qui signifie qu'il a la m??me valeur quel que soit le sens dans lequel elle est mesur??e. Observations des ??missions de nucl??aire les niveaux d'??nergie en fonction de l'orientation des ??metteurs noyaux dans un champ magn??tique (voir Hughes-Drever exp??rience), et de rotation r??sonateurs optiques (voir exp??riences ?? r??sonateur) ont mis des limites strictes sur la possible anisotropie bidirectionnelle.
Limite sup??rieure sur les vitesses
Selon la relativit?? restreinte, l'??nergie d'un objet avec reste masse m et la vitesse v est donn??e par γmc 2, o?? γ est le facteur de Lorentz d??fini ci-dessus. Lorsque v est z??ro, γ est ??gal ?? un, donnant lieu ?? la c??l??bre E = mc 2 formule pour ??quivalence masse-??nergie. Le facteur de γ tend vers l'infini comme approche v c, et il faudrait une quantit?? infinie d'??nergie pour acc??l??rer un objet de masse ?? la vitesse de la lumi??re. La vitesse de la lumi??re est la limite sup??rieure pour les vitesses des objets dont la masse reste positive. Ce est ??tablie exp??rimentalement dans de nombreux les tests de l'??nergie relativiste et l'??lan.
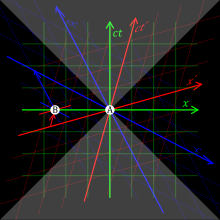
Plus g??n??ralement, il est normalement impossible pour obtenir des informations ou de l'??nergie de se d??placer plus vite que c. Un argument en faveur de cette d??coule de l'implication de contre-intuitif de la relativit?? sp??ciale connue sous le nom relativit?? de la simultan??it??. Si la distance spatiale entre deux ??v??nements A et B est sup??rieure ?? l'intervalle de temps entre eux, multipli?? par c puis il ya des cadres de r??f??rence dans laquelle A, B pr??c??de autres dans lesquels B pr??c??de A, et d'autres o?? elles sont simultan??es. En cons??quence, si quelque chose se d??pla??aient plus vite que c par rapport ?? un r??f??rentiel inertiel, il serait voyageant ?? reculons dans le temps par rapport ?? un autre cadre, et causalit?? serait viol??. Dans un tel cadre de r??f??rence, un ??effet?? a pu ??tre observ??e avant sa ??cause??. Une telle violation de la causalit?? n'a jamais ??t?? enregistr??e, et conduirait ?? paradoxes comme le antitelephone tachyonique.
Plus rapide que la lumi??re des observations et des exp??riences
Il ya des situations dans lesquelles il peut sembler que la mati??re, l'??nergie ou l'information circule ?? des vitesses sup??rieures ?? c, mais ils ne le font pas. Par exemple, comme on le verra dans la propagation de la lumi??re dans un milieu section ci-dessous, de nombreuses vitesses des ondes peuvent d??passer c. Par exemple, le vitesse de phase de rayons X ?? travers la plupart des verres peuvent r??guli??rement exc??der c, mais ces ondes ne transmettre aucune information.
Si un faisceau laser est balay?? rapidement ?? travers un objet ??loign??, la tache lumineuse peut aller plus vite que c, bien que le mouvement initial de la tache est retard?? en raison du temps que met la lumi??re pour se rendre ?? l'objet distant ?? la vitesse c. Toutefois, les seules entit??s physiques qui se d??placent sont le laser et sa lumi??re ??mise, qui se d??place ?? la vitesse c du laser pour les diff??rentes positions de la place. De m??me, une ombre projet??e sur un objet distant peut ??tre amen?? ?? se d??placer plus vite que c, apr??s un retard dans le temps. Dans les deux cas ne importe quel mati??re, l'??nergie, ou des informations touristiques vite que la lumi??re.
Le taux de variation de la distance entre deux objets dans un cadre de r??f??rence par rapport ?? laquelle les deux sont mobiles (leur vitesse de fermeture) peut avoir une valeur sup??rieure ?? c. Toutefois, cela ne repr??sente pas la vitesse d'un objet unique, telle que mesur??e dans un r??f??rentiel inertiel unique.
Certains effets quantiques semblent ??tre transmise instantan??ment et donc plus rapide que c, comme dans le Paradoxe EPR. Un exemple consiste ?? deux ??tats quantiques de particules qui peuvent ??tre emp??tr??. Jusqu'?? ce que l'une des particules est observ??e, ils existent dans un superposition de deux ??tats quantiques. Si les particules sont s??par??es et l'??tat quantique de une particule est observ??e, l'??tat quantique de l'autre particule est d??termin?? instantan??ment (ce est ?? dire, plus vite que la lumi??re peut voyager d'une particule ?? l'autre). Toutefois, il est impossible de contr??ler les ??tat quantique la premi??re particule prendra quand elle est observ??e, afin que l'information ne peut ??tre transmise de cette mani??re.
Un autre effet quantique qui pr??dit l'apparition de plus rapide que la lumi??re vitesses est appel?? Effet Hartman; sous certaines conditions, le temps n??cessaire pour un particule virtuelle ?? ?? travers une barri??re tunnel est constante, ind??pendamment de l'??paisseur de la barri??re. Il pourrait en r??sulter une particule virtuelle traversant un grand ??cart plus rapidement que la lumi??re. Cependant, aucune information ne peut ??tre envoy??e en utilisant cet effet.
Soi-disant supraluminique mouvement est consid??r?? dans certains objets astronomiques, comme le jets relativistes de galaxies de radio et de quasars. Cependant, ces jets ne se d??placent pas ?? une vitesse sup??rieure ?? la vitesse de la lumi??re: le mouvement supraluminique apparente est un effet de projection caus?? par des objets en mouvement pr??s de la vitesse de la lumi??re et se approchant de la Terre ?? un petit angle avec la ligne de vis??e: car la lumi??re qui a ??t?? ??mise lorsque le jet a ??t?? plus loin pris plus de temps pour atteindre la Terre, le temps entre deux observations successives correspond pour un temps plus long entre les instants o?? les rayons lumineux sont ??mis.
Dans les mod??les de l'univers en expansion, les galaxies plus lointaines sont de l'autre, plus vite ils se s??parent. Ce recul ne est pas d?? au mouvement ?? travers l'espace, mais plut??t ?? la expansion de l'espace lui-m??me. Par exemple, les galaxies loin de la terre semblent se ??loigner de la Terre avec une vitesse proportionnelle ?? leur distance. Au-del?? d'une limite appel??e Sph??re Hubble, la vitesse ?? laquelle leur distance de l'augmentation de la Terre devient sup??rieure ?? la vitesse de la lumi??re.
En Septembre 2011, les physiciens travaillant sur le OPERA a publi?? des r??sultats qui sugg??raient de poutres neutrinos avait voyag?? de CERN (Gen??ve, Suisse) ?? LNGS (au Gran Sasso, Italie) plus rapide que la vitesse de la lumi??re. Ces r??sultats, parfois d??nomm?? plus vite que la lumi??re anomalie des neutrinos, ont ensuite ??t?? d??termin??e-sous r??serve de confirmation ?? ??tre le r??sultat d'une erreur de mesure.
Propagation de la lumi??re
En la physique classique, la lumi??re est d??crit comme un type de onde ??lectromagn??tique . Le comportement classique de la champ ??lectromagn??tique est d??crit par les ??quations de Maxwell , qui pr??disent que la vitesse avec laquelle c ondes ??lectromagn??tiques (comme la lumi??re) se propagent ?? travers le vide est li??e ?? la ε constante ??lectrique 0 et le μ magn??tique constant 0 par l'??quation c = 1 / √ ε 0 μ 0. Dans moderne physique quantique , le champ ??lectromagn??tique est d??crite par la th??orie de ??lectrodynamique quantique (QED). Dans cette th??orie, la lumi??re est d??crit par les excitations fondamentales (ou quanta) du champ ??lectromagn??tique, appel??s photons . Dans QED, les photons sont particules sans masse et ainsi, selon la relativit?? restreinte, ils se d??placent ?? la vitesse de la lumi??re dans le vide.
Extensions de QED dans lequel le photon a une masse ont ??t?? consid??r??s. Dans une telle th??orie, sa vitesse d??pendrait de sa fr??quence, et la vitesse c invariant de la relativit?? restreinte serait alors la limite sup??rieure de la vitesse de la lumi??re dans le vide. Aucune variation de la vitesse de la lumi??re avec une fr??quence a ??t?? observ??e dans des tests rigoureux, mettre des limites strictes sur la masse du photon. La limite obtenue d??pend du mod??le utilis??: si le photon massif est d??crit par Proca th??orie, l'exp??rimentale limite sup??rieure pour sa masse est d'environ 10 -57 g; si la masse de photons est produite par un M??canisme de Higgs, la limite sup??rieure exp??rimental est moins nette, m ≤ 10 -14 eV / c 2 (environ 2 ?? 10 -47 g).
Une autre raison de la vitesse de la lumi??re ?? varier avec sa fr??quence serait l'??chec de la relativit?? restreinte d'appliquer arbitrairement petites ??chelles, comme pr??dit par certaines th??ories propos??es la gravit?? quantique. En 2009, l'observation du spectre sursaut gamma GRB 090510 n'a trouv?? aucune diff??rence dans les vitesses de photons de diff??rentes ??nergies, confirmant que l'invariance de Lorentz est v??rifi??e au moins jusqu'?? l'??chelle de la Longueur de Planck (l P = √ ?? G / c 3 ≈ 1,6163 x 10 -35 m) divis??e par 1,2.
Dans un milieu
Dans un milieu, habituellement la lumi??re ne se propage pas ?? une vitesse ??gale ?? c; en outre, diff??rents types d'ondes de lumi??re se rendront ?? des vitesses diff??rentes. La vitesse ?? laquelle les cr??tes et les creux individuels d'un onde plane (une onde de remplissage de l'espace entier, avec seulement une fr??quence) se propagent est appel?? le vitesse de phase v p. Un signal physique r??elle avec une ??tendue finie (une impulsion de lumi??re) se d??place ?? une vitesse diff??rente. La plus grande partie de l'impulsion se d??place ?? la vitesse de groupe v g, et sa premi??re partie se d??place ?? la avant vitesse v f.

La vitesse de phase est importante pour d??terminer comment une onde lumineuse se d??place dans un mat??riau ou d'un mat??riau ?? un autre. Il est souvent repr??sent?? en termes d'un indice de r??fraction. L'indice de r??fraction d'un mat??riau est d??finie comme le rapport de c ?? la vitesse de phase v p dans le mat??riau: indices de r??fraction plus grands indiquent des vitesses inf??rieures. L'indice de r??fraction d'un mat??riau peut d??pendre de la fr??quence, l'intensit?? de la lumi??re, polarisation ou de la direction de propagation; dans de nombreux cas, cependant, il peut ??tre consid??r?? comme une constante d??pendant du mat??riau. L' indice de r??fraction de l'air est d'environ 1,0003. Milieux les plus denses, tels que l'eau, le verre et diamants , ont des indices de r??fraction de l'ordre de 1,3, 1,5 et 2,4, respectivement, pour la lumi??re visible. Dans les mat??riaux exotiques comme Condensats de Bose-Einstein proche du z??ro absolu, la vitesse efficace de la lumi??re peut ??tre ?? seulement quelques m??tres par seconde. Cependant, cela repr??sente absorption et re-rayonnement d??lai entre les atomes, comme le font toutes les vitesses plus lente que c dans les substances mat??rielles. Comme un exemple extr??me de cette lumi??re "ralentir" dans la mati??re, deux ??quipes ind??pendantes de physiciens pr??tendent apporter la lumi??re ?? un "arr??t complet" en le faisant passer ?? travers un condensat de Bose-Einstein de l'??l??ment de rubidium , une ??quipe de Universit?? de Harvard et le Rowland Institut pour la science dans Cambridge, Mass., Et l'autre ?? la Centre Harvard-Smithsonian pour l'astrophysique, ??galement ?? Cambridge. Toutefois, la description populaire de l'??tre de lumi??re "arr??t??" dans ces exp??riences se r??f??re uniquement ?? la lumi??re ??tant stock??e dans les ??tats excit??s d'atomes, puis r??-??mise ?? un moment arbitraire plus tard, stimul??e par une seconde impulsion laser. Pendant le temps qu'il avait "arr??t??", il avait cess?? d'??tre la lumi??re. Ce type de comportement est g??n??ralement microscope vrai de tous les milieux transparents qui "ralentir" la vitesse de la lumi??re.
Dans les mat??riaux transparents, l'indice de r??fraction est g??n??ralement sup??rieure ?? 1, ce qui signifie que la vitesse de phase est inf??rieure ?? c. En d'autres mat??riaux, il est possible de l'indice de r??fraction de devenir inf??rieure ?? 1 pour certaines fr??quences; dans certains mat??riaux exotiques, il est m??me possible de l'indice de r??fraction de devenir n??gative. L'exigence que la causalit?? ne est pas viol??e implique que les parties r??elles et imaginaires de la constante di??lectrique d'un mat??riau, correspondant respectivement ?? l'indice de r??fraction et ?? la coefficient d'att??nuation, sont li??s par le Relations de Kramers-Kronig. En termes pratiques, cela signifie que dans un mat??riau ?? indice de r??fraction inf??rieur ?? 1, l'absorption de l'onde est si rapide qu'aucun signal ne peut ??tre envoy?? plus rapide que c.
Une impulsion avec diff??rentes vitesses de groupe et de phase (ce qui se produit si la vitesse de phase ne est pas la m??me pour toutes les fr??quences de l'impulsion frottis) dans le temps, un processus connu sous le nom dispersion. Certains mat??riaux ont une vitesse exceptionnellement faible (voire nulle) groupe pour les ondes lumineuses, un ph??nom??ne appel?? lumi??re lente, qui a ??t?? confirm?? dans diverses exp??riences. Les vitesses de groupe, oppos??es d??passant c, a ??galement ??t?? montr?? dans l'exp??rience. Il devrait m??me ??tre possible pour la vitesse de groupe de devenir infinie ou n??gative, avec des impulsions voyager instantan??ment ou en arri??re dans le temps.
Aucune de ces options, cependant, permettre la transmission des informations plus vite que c. Il est impossible de transmettre des informations avec une lumi??re d'impulsion plus vite que la vitesse de la premi??re partie de l'impulsion (la vitesse avant). On peut montrer que ce est (sous certaines hypoth??ses) toujours ??gale ?? c.
Il est possible pour une particule de se d??placer ?? travers un milieu plus rapide que la vitesse de phase de la lumi??re dans ce milieu (mais toujours plus lentement que c). Lorsqu'un particules charg??es fait que, dans un un mat??riau di??lectrique, soit l'??quivalent d'une ??lectromagn??tique onde de choc, connu sous le nom Rayonnement Tcherenkov, est ??mis.
Effets pratiques de la finitude
La vitesse de la lumi??re est de l'int??r??t pour les communications : l'aller simple et aller-retour temps de retard sont sup??rieurs ?? z??ro. Cela se applique de la petite ?? ??chelles astronomiques. D'autre part, certaines techniques d??pendent de la vitesse finie de la lumi??re, par exemple dans les mesures de distance.
Petites ??chelles
En supercalculateurs, la vitesse de la lumi??re impose une limite sur combien rapidement les donn??es peuvent ??tre envoy??es entre processeurs . Si un processeur fonctionne ?? une gigahertz, un signal ne peut voyager un maximum d'environ 30 centim??tres (1 pi) en un seul cycle. Les transformateurs doivent donc ??tre plac??s ?? proximit?? les uns des autres pour minimiser la latence de communication; cela peut causer des difficult??s avec refroidissement. Si des fr??quences d'horloge continuent d'augmenter, la vitesse de la lumi??re finira par devenir un facteur limitant pour la conception interne de simples puces .
De grandes distances sur Terre
Par exemple, compte tenu de la circonf??rence ??quatorial de la Terre est d'environ 40075 km et c environ 300.000 km / s, le plus bref d??lai th??orique d'un ??l??ment d'information ?? parcourir la moiti?? du globe long de la surface est d'environ 67 millisecondes. Lorsque la lumi??re se d??place dans le monde entier dans une fibre optique , le temps de transit est plus r??elle, en partie parce que la vitesse de la lumi??re est plus lente d'environ 35% dans une fibre optique, en fonction de son indice de r??fraction n. En outre, les lignes droites se produisent rarement dans des situations de communication mondiaux, et les retards sont cr????s lorsque le signal passe par un commutateur ou un signal r??g??n??rateur ??lectronique.
Vols spatiaux et l'astronomie
De m??me, les communications entre la Terre et spatiaux ne sont pas instantan??s. Il ya un bref d??lai de la source au r??cepteur, qui devient plus perceptible que les distances augmentent. Ce retard ??tait importante pour les communications entre contr??le au sol et Apollo 8 quand il est devenu le premier vaisseau spatial habit?? en orbite autour de la Lune: pour chaque question, la station de contr??le au sol a d?? attendre au moins trois secondes pour la r??ponse ?? arriver. Le d??lai de communication entre la Terre et Mars peut varier entre cinq et vingt minutes en fonction des positions relatives des deux plan??tes. En cons??quence de cela, si un robot sur la surface de Mars devait rencontrer un probl??me, ses contr??leurs humains ne seraient pas au courant jusqu'?? ce que au moins cinq minutes plus tard, et peut-??tre jusqu'?? vingt minutes plus tard; il prendrait alors une p??riode de cinq ?? vingt minutes pour les instructions de voyager de la Terre ?? Mars.
NASA doit attendre plusieurs heures pour obtenir des informations ?? partir d'une sonde en orbite autour de Jupiter, et si elle a besoin de corriger une erreur de navigation, le correctif ne sera pas arriver ?? l'engin spatial pour un montant ??gal de temps, cr??ant un risque de la correction ne pas arriver ?? temps.
Recevoir d'autres signaux de lumi??re et de sources astronomiques ??loign??s peut m??me prendre beaucoup plus longtemps. Par exemple, il a fallu 13 milliards (13 ?? 10 9) ans pour la lumi??re pour se rendre ?? la Terre des galaxies lointaines vues dans le Hubble Ultra images champ profond. Ces photographies, prises aujourd'hui, de capturer des images des galaxies comme ils sont apparus il ya 13 milliards d'ann??es, lorsque l'Univers avait moins d'un milliard d'ann??es. Le fait que les objets plus ??loign??s semblent ??tre plus jeunes, en raison de la vitesse finie de la lumi??re, permet aux astronomes de d??duire la l'??volution des ??toiles, des galaxies, et de l'univers lui-m??me.
Distances astronomiques sont parfois exprim??s en ann??es-lumi??re, en particulier dans populaire publications scientifiques et les m??dias. Une ann??e-lumi??re est la lumi??re voyage ?? distance en un an, autour 9461000000000 km, 5879 billion miles, ou 0,3066 parsecs. En chiffres ronds, une ann??e-lumi??re est pr??s 10000000000000 kilom??tres ou pr??s de 6 trillion miles. Proxima Centauri , l'??toile la plus proche de la Terre apr??s le Soleil, est d'environ 4,2 ann??es-lumi??re.
Mesure de distance
Radar syst??mes mesurent la distance ?? une cible par le temps qu'il faut une impulsion des ondes radio pour revenir ?? l'antenne radar apr??s avoir ??t?? r??fl??chi par la cible: la distance ?? la cible est la moiti?? du voyage aller-retour du temps de transit multipli?? par la vitesse de la lumi??re . Un Global Positioning System (GPS) mesure sa distance jusqu'aux satellites GPS en fonction de combien de temps il faut ?? un signal radio ?? arriver de chaque satellite, et de ces distances calcule la position du r??cepteur. Parce que la lumi??re parcourt environ 300000 km (186000 milles) en une seconde, ces mesures de petites fractions de seconde doivent ??tre tr??s pr??cis. Le Lunar Laser Ranging Experiment, astronomie radar et le Profonde Network Space d??terminer les distances vers la Lune, les plan??tes et d'engins spatiaux, respectivement, en mesurant aller-retour le temps de transit.
Mesures
Il ya diff??rentes fa??ons de d??terminer la valeur de c. Une fa??on consiste ?? mesurer la vitesse r??elle ?? laquelle les ondes lumineuses se propagent, ce qui peut ??tre fait dans diff??rentes configurations astronomiques et terrestres. Cependant, il est ??galement possible de d??terminer ?? partir de c d'autres lois physiques o?? il appara??t, par exemple, en d??terminant les valeurs des constantes ??lectromagn??tiques ε 0 et μ 0 et en utilisant leur rapport ?? c. Historiquement, les r??sultats les plus pr??cis ont ??t?? obtenus en d??terminant s??par??ment la fr??quence et la longueur d'onde d'un faisceau lumineux, avec leur produit ??galant c.
En 1983, le compteur a ??t?? d??fini comme "la longueur du trajet parcouru par la lumi??re dans le vide pendant un intervalle de temps de 1/299,792,458 d'une seconde", la fixation de la valeur de la vitesse de la lumi??re ?? 299 792 458 m / s, par d??finition, comme d??crit ci-dessous . En cons??quence, des mesures pr??cises de la vitesse de la lumi??re donnent une r??alisation pr??cise de l'appareil plut??t qu'une valeur pr??cise de c.
Mesures astronomiques
L'espace est un cadre naturel pour mesurer la vitesse de la lumi??re en raison de sa grande ??chelle et presque parfait vide. Typiquement, on mesure le temps n??cessaire ?? la lumi??re pour parcourir une certaine distance de r??f??rence dans le syst??me solaire , comme le rayon de l'orbite de la Terre. Par le passé, de telles mesures peuvent être effectuées de façon assez précise, par rapport à la précision avec laquelle la longueur de la distance de référence est connue dans des unités à base de terre. Il est de coutume d'exprimer les résultats en unités astronomiques (UA) par jour. Une unité astronomique est approximativement la distance moyenne entre la Terre et le Soleil; elle ne repose pas sur le Système international d'unités. Parce que l'UA détermine une longueur réelle, et ne repose pas sur le temps de vol comme les unités SI, des mesures modernes de la vitesse de la lumière en unités astronomiques par jour peuvent être comparés à la valeur définie de c dans le Système international d'unités .
Ole Christensen Rømer utilisé une mesure astronomique de faire la première estimation quantitative de la vitesse de la lumière. Lorsque mesurée à partir de la Terre, les périodes de lunes en orbite autour d'une planète lointaine sont plus courts lorsque la Terre se rapproche de la planète que lorsque la Terre est en recul de celui-ci. La distance parcourue par la lumière de la planète (ou sa lune) à la Terre est plus court lorsque la Terre est sur ??????le point de son orbite le plus proche de sa planète que lorsque la Terre est au point le plus éloigné de son orbite, la différence de distance étant le diamètre de l'orbite de la Terre autour du Soleil La variation observée dans la période orbitale de la lune est en fait la différence dans le temps nécessaire pour traverser la lumière distance plus courte ou plus longue. Rømer observé cet effet pour Jupiter plus intime lune de Io et en a déduit que la lumière prend 22 minutes pour traverser le diamètre de l'orbite de la Terre.
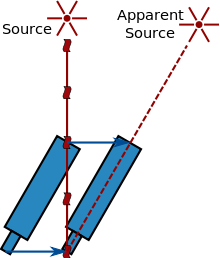
Une autre m??thode consiste ?? utiliser l' aberration de la lumi??re , d??couvert et expliqu?? par James Bradley dans le 18??me si??cle. Cet effet r??sulte de l' addition vectorielle de la vitesse de la lumi??re arrivant d'une source lointaine (comme une ??toile) et la vitesse de son observateur (voir sch??ma ?? droite). Un observateur se d??pla??ant voit ainsi la lumi??re provenant d'une direction l??g??rement diff??rente et voit la source dans une position d??cal??e ?? partir de sa position d'origine en cons??quence. Depuis la direction de la vitesse de la Terre change continuellement que la Terre tourne autour du Soleil, cet effet entra??ne la position apparente des ??toiles pour se d??placer. De l'??cart angulaire dans la position d'??toiles (au maximum 20,5 secondes d'arc), il est possible d'exprimer la vitesse de la lumi??re en termes de la vitesse de la Terre autour du Soleil, qui, avec la longueur connue d'une ann??e peut ??tre facilement converti en le temps n??cessaire pour voyager entre le Soleil et la Terre. En 1729, Bradley a utilis?? cette m??thode pour obtenir que la lumi??re a voyag?? 10 210 fois plus vite que la Terre dans son orbite (la figure moderne est 10 066 fois plus rapide) ou, de fa??on ??quivalente, qu'il faudrait l??gers 8 minutes 12 secondes de voyager entre le Soleil et la Terre.
Aujourd'hui, le ??temps de lumi??re pour unit?? de distance" -le inverse de c, exprim??e en secondes par astronomique unit?? est mesur??e en comparant le temps pour les signaux radio atteignent vaisseau diff??rent dans le syst??me solaire, avec leur position calcul??e ?? partir des effets gravitationnels de Soleil et des plan??tes diff??rentes. En combinant plusieurs de ces mesures, un meilleure valeur ajustement pour le moment la lumi??re par unit?? de distance est obtenue. En 2009, la meilleure estimation, approuv?? par le Union astronomique internationale (UAI), est:
- le temps de lumi??re pour unit?? de distance: 499,004 7 83 8 36 (10) s
- c=0,00200398880410 (4) de l'UA / s=173,144632674 (3) de l'UA / jour.
L'incertitude relative à ces mesures est de 0,02 parties par milliard (2 × 10 -11 ), l'équivalent de l'incertitude dans les mesures basés sur la Terre de longueur par interférométrie. Etant donné que l'appareil de mesure est définie comme étant la longueur parcourue par la lumière dans un certain intervalle de temps, la mesure du temps de la lumière à distance de l'unité peut aussi être interprété comme mesure de la longueur d'un UA en mètres.
Temps de techniques de vol
Une méthode de mesure de la vitesse de la lumière est de mesurer le temps nécessaire à la lumière de se rendre à un miroir à une distance et à l'arrière connue. Ceci est le principe de fonctionnement derrière l' appareil Fizeau-Foucault développé par Hippolyte Fizeau et Léon Foucault.
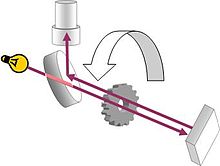
La configuration comme utilisé par Fizeau est constitué d'un faisceau de lumière dirigée vers un miroir 8 km (5 miles) de distance. Sur le chemin de la source vers le miroir, le faisceau passe à travers une roue dentée rotative. A une certaine vitesse de rotation, le faisceau traverse un fossé sur le chemin et l'autre sur le chemin du retour, mais à des taux légèrement plus élevés ou plus faibles, le faisceau frappe une dent et ne passe pas par la roue. Connaissant la distance entre la roue et le miroir, le nombre de dents sur la roue, et la vitesse de rotation, la vitesse de la lumière peut être calculée.
La méthode de Foucault remplace la roue dentée par un miroir rotatif. Parce que le miroir continue à tourner alors que la lumière se déplace vers le miroir lointain et arrière, la lumière est réfléchie par le miroir rotatif à un angle différent sur ??????sa sortie qu'elle ne l'est sur ??????son chemin du retour. De cette différence d'angle, la vitesse de rotation connue et la distance au miroir lointain la vitesse de la lumière peuvent être calculés.
De nos jours, en utilisant les oscilloscopes avec des résolutions de temps de moins d'une nanoseconde, la vitesse de la lumière peut être mesurée directement en chronométrant le retard d'une impulsion de lumière provenant d'un laser ou une LED réfléchie par un miroir. Cette méthode est moins précis (avec des erreurs de l'ordre de 1%) que les autres techniques modernes, mais il est parfois utilisé comme une expérience de laboratoire dans les classes collège de physique.
Constantes électromagnétiques
Une option pour dériver c qui ne dépend pas directement sur ??????une mesure de la propagation des ondes électromagnétiques est d'utiliser la relation entre c et la permittivité du vide ?? 0 et la perméabilité du vide ?? 0 établi par la théorie de Maxwell: c 2 = 1 / ( e 0 u 0 ). La permittivité du vide peut être déterminée en mesurant la capacité et les dimensions d'un condensateur, tandis que la valeur de la perméabilité à vide est fixée à exactement 4?? x 10 -7 H · m -1 à travers la définition de l' ampère. Rosa et Dorsey utilisé cette méthode en 1907 pour trouver une valeur de 299 710 ± 22 km / s .
résonance de la cavité

Une autre façon de mesurer la vitesse de la lumière est de mesurer indépendamment la fréquence f et de longueur d'onde ?? d'une onde électromagnétique dans le vide. La valeur de c peut alors être trouvé en utilisant la relation c = f?? . Une option consiste à mesurer la fréquence de résonance d'un résonateur à cavité. Si les dimensions de la cavité de résonance sont également connus, ceux-ci peuvent être utilisés à déterminer la longueur d'onde de l'onde. En 1946, Louis Essen et AC Gordon-Smith établir la fréquence pour une variété de modes normaux de micro-ondes d'une cavité micro-ondes de dimensions précisément connues. Les dimensions ont été établies avec une précision d'environ ± 0,8 um en utilisant des jauges calibrées par interférométrie. Comme la longueur d'onde des modes est connu d'après la géométrie de la cavité et de la théorie électromagnétique , la connaissance des fréquences associées activer un calcul de la vitesse de la lumière.
Le résultat Essen-Gordon-Smith, 299 792 ± 9 km / s , était nettement plus précis que ceux trouvés par des techniques optiques. En 1950, des mesures répétées par Essen établis à la suite de 299,792.5 ± 3,0 km / s .
Une démonstration des ménages de cette technique est possible, en utilisant un four à micro-ondes et de la nourriture comme des guimauves ou la margarine: si le plateau est enlevé de sorte que la nourriture ne bouge pas, il va cuire le plus rapide à des ventres (les points où l'amplitude de l'onde est le plus grand), où elle commence à fondre. La distance entre deux de ces points est la moitié de la longueur d'onde des micro-ondes; par la mesure de cette distance et en multipliant la longueur d'onde de la fréquence de micro-ondes (habituellement affichée sur l'arrière du four, typiquement 2450 MHz), la valeur de c peut être calculé », souvent avec une erreur inférieure à 5%."
Interférométrie
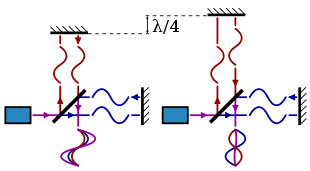
L'interférométrie est une autre méthode pour trouver la longueur d'onde du rayonnement électromagnétique pour déterminer la vitesse de la lumière. Un faisceau de lumière cohérente (par exemple à partir d'un laser ), avec une fréquence connue ( f ), est divisé à suivre deux voies, puis recombinée. En ajustant la longueur du chemin tout en observant le motif d'interférence et en mesurant soigneusement la variation de longueur de chemin, la longueur d'onde de la lumière ( ?? ) peut être déterminée. La vitesse de la lumière est alors calculée en utilisant l'équation c = ??f .
Avant l'avènement de la technologie laser, cohérentes radios sources ont été utilisées pour les mesures d'interférométrie de la vitesse de la lumière. Cependant détermination interférométrique de longueur d'onde devient moins précise de longueur d'onde et les expériences ont été ainsi limitée par la précision en longueur d'onde longue (~ 0,4 cm) des ondes radio. La précision peut être améliorée en utilisant de la lumière avec une longueur d'onde plus courte, mais alors il devient difficile de mesurer directement la fréquence de la lumière. Un moyen de contourner ce problème est de commencer avec un signal à basse fréquence dont la fréquence peut être mesurée avec précision, et à partir de ce signal progressivement synthétiser des signaux haute fréquence dont la fréquence peut alors être lié au signal d'origine. Un laser peut alors être verrouillé sur la fréquence et la longueur d'onde peut être déterminée en utilisant l'interférométrie. Cette technique était due à un groupe au National Bureau of Standards (NBS) (qui devint plus tard NIST). Ils l'ont utilisé en 1972 pour mesurer la vitesse de la lumière dans le vide avec une incertitude fractionnaire de 3,5 × 10 -9 .
Histoire
| 1675 | Romer etHuygens, lunes de Jupiter | 220000 |
| 1729 | James Bradley, aberration de la lumière | 301000 |
| 1849 | Hippolyte Fizeau, roue dentée | 315000 |
| 1862 | Léon Foucault, miroir rotatif | 298 000±500 |
| 1907 | Rosa et Dorsey,EMconstantes | 299 710±30 |
| 1926 | Albert Michelson, miroir rotatif | 299 796±4 |
| 1950 | Essen et Gordon-Smith, résonateurs à cavité | 299,792.5±3.0 |
| 1958 | KD Froome, radio interférométrie | 299,792.50±0,10 |
| 1972 | Evensonet al., interférométrie laser | 299,792.4562±0,0011 |
| 1983 | 17 e CGPM, définition du mètre | 299,792.458(exacte) |
Jusqu'?? ce que le début de la période moderne, on ne sait pas si la lumière a voyagé instantanément ou à une vitesse finie très rapide. Le premier examen enregistrée existante de ce sujet était dans la Grèce antique . Les anciens Grecs, les savants musulmans et des scientifiques européens classiques débattu longtemps jusqu'à ce que Rømer a fourni le premier calcul de la vitesse de la lumière. La théorie de la relativité d'Einstein spécial a conclu que la vitesse de la lumière est constante indépendamment de l'un de cadre de référence. Depuis lors, les scientifiques ont fourni des mesures de plus en plus précises.
Premi??re histoire
Empédocle a été le premier à affirmer que la lumière a une vitesse finie. Il a maintenu que la lumière était quelque chose en mouvement, et doit donc prendre un certain temps à voyager. Aristote a fait valoir, au contraire, que «la lumière est due à la présence de quelque chose, mais il est pas un mouvement". Euclide et Ptolémée avancé l' émission théorie de la vision, où la lumière est émise à partir de l'??il, permettant ainsi de vue. Basé sur cette théorie, Héron d'Alexandrie a fait valoir que la vitesse de la lumière doit être infinie parce que les objets lointains tels que les étoiles apparaissent immédiatement après l'ouverture des yeux.
Les premiers philosophes musulmans ont d'abord convenu avec le vision aristotélicienne que la lumière avait pas de vitesse de Voyage. En 1021, Alhazen (Ibn al-Haytham) a publié le livre de l'optique , dans lequel il a présenté une série d'arguments rejetant la théorie de l'émission en faveur de la théorie de l'intromission maintenant accepté de vision, dans laquelle se déplace la lumière provenant d'un objet dans l'??il. Cela a conduit Alhazen de proposer que la lumière doit avoir une vitesse finie, et que la vitesse de la lumière est variable, en baisse dans les organes les plus denses. Il a fait valoir que la lumière est une matière importante, la propagation de qui nécessite du temps, même si cela est inaccessible à nos sens. Toujours dans le 11ème siècle, Al-Biruni convenu que la lumière a une vitesse finie, et observé que la vitesse de la lumière est beaucoup plus rapide que la vitesse du son.
Au 13??me si??cle, Roger Bacon a fait valoir que la vitesse de la lumière dans l'air était pas infinie, en utilisant des arguments philosophiques soutenues par la rédaction de Alhazen et Aristote. Dans les années 1270, Witelo envisagé la possibilité de lumière se déplaçant à une vitesse infinie dans le vide, mais le ralentissement dans les organes les plus denses.
Au début du 17e siècle, Johannes Kepler croyait que la vitesse de la lumière était infinie, puisque l'espace vide ne présente aucun obstacle. René Descartes a fait valoir que si la vitesse de la lumière était finie, le Soleil, la Terre et la Lune serait sensiblement sur l'alignement lors d'une éclipse lunaire . Depuis tels désalignement avait pas été observé, Descartes a conclu la vitesse de la lumière était infinie. Descartes spéculé que si la vitesse de la lumière ont été trouvés être finie, tout son système de la philosophie pourrait être démoli.
Les premières tentatives de mesure
En 1629, Isaac Beeckman a proposé une expérience dans laquelle une personne observe le flash d'un canon se reflétant sur ??????un miroir d'environ un mile (1,6 km). En 1638, Galilée a proposé une expérience, avec une demande apparente d'avoir effectué il quelques années plus tôt, pour mesurer la vitesse de la lumière en observant le délai entre la découverte d'une lanterne et de sa perception à une certaine distance. Il était incapable de distinguer si Voyage de lumière était instantanée ou non, mais a conclu que si il n'y avait pas, il doit néanmoins être extraordinairement rapide. L'expérience de Galileo a été réalisée par l' Accademia del Cimento de Florence, en Italie, en 1667, avec les lanternes séparés par environ un mile, mais aucun délai n'a été observée. Le retard réel dans cette expérience aurait été d'environ 11 microsecondes.
La première estimation quantitative de la vitesse de la lumière a été faite en 1676 par Romer (voir la détermination de Romer de la vitesse de la lumière). De l'observation que les périodes de plus intime lune de Jupiter Io semblaient être plus courte quand la Terre approchait Jupiter que lorsque recul de celui-ci, il a conclu que la lumière voyage à une vitesse finie, et estime qu'il faut de lumière 22 minutes pour traverser le diamètre de l'orbite de la Terre. Christiaan Huygens combiné cette estimation avec une estimation pour le diamètre de l'orbite de la Terre pour obtenir une estimation de la vitesse de la lumière de 220000 km / s , 26% inférieure à la valeur réelle.
Dans ses 1704 livres Opticks , Isaac Newton a rapporté les calculs de Romer de la vitesse finie de la lumière et donne une valeur de "sept ou huit minutes" pour le temps pris pour la lumière pour aller du Soleil à la Terre (la valeur moderne est de 8 minutes 19 secondes). Newton a demandé si les ombres des éclipses de Romer ont été colorés; entendre qu'elles ne sont pas, at-il conclu les différentes couleurs sont rendus à la même vitesse. En 1729, James Bradley a découvert l' aberration de la lumière . De cet effet il a déterminé que la lumière doit parcourir 10 210 fois plus vite que la Terre dans son orbite (la figure moderne est 10 066 fois plus rapide) ou, de façon équivalente, que cela prendrait légers 8 minutes 12 secondes pour voyager entre le Soleil et la Terre.
Connexions avec l'électromagnétisme
Au 19??me si??cle Hippolyte Fizeau a développé une méthode pour déterminer la vitesse de la lumière en fonction de mesures de temps de vol sur Terre et a rapporté une valeur de 315000 km / s . Sa méthode a été améliorée par Léon Foucault qui a obtenu une valeur de 298000 km / s en 1862. En l'an 1856, Wilhelm Eduard Weber et Rudolf Kohlrausch mesuré le rapport des unités électromagnétiques et de charge électrostatique, 1 / ??? e 0 u 0 , en déchargeant une bouteille de Leyde , et a constaté que sa valeur numérique était très proche de la vitesse de la lumière mesurée directement par Fizeau. L'ann??e suivante Gustav Kirchhoff calculé que un signal électrique dans un sans résistance fil se déplace le long du fil à cette vitesse. Au début des années 1860, Maxwell a montré que, selon la théorie de l'électromagnétisme qui il travaillait, que les ondes électromagnétiques se propagent dans le vide à une vitesse égale à ce qui précède rapport Weber / Kohrausch, et ??????attirer l'attention sur la proximité numérique de cette valeur la vitesse de la lumière mesurée par Fizeau, il a proposé que la lumière est en fait une onde électromagnétique.
"Éther Luminiferous"

On pensait à l'époque que l'espace vide a été rempli avec un milieu de fond appelé l' éther luminiferous dans lequel le champ électromagnétique existait. Certains physiciens pensaient que cet éther a agi comme un cadre privilégié de référence pour la propagation de la lumière et il devrait donc être possible de mesurer le mouvement de la Terre par rapport à ce milieu, par la mesure de l'isotropie de la vitesse de la lumière. Au début des années 1880, plusieurs expériences ont été effectuées pour tenter de détecter cette motion, dont le plus célèbre est l'expérience réalisée par Albert Michelson et Edward Morley en 1887. Le mouvement détecté était toujours inférieure à l'erreur d'observation. Les expériences modernes indiquent que la vitesse dans les deux sens de la lumière est isotrope (le même dans tous les sens) à moins de 6 nanomètres par seconde. En raison de cette expérience Hendrik Lorentz a proposé que le mouvement de l'appareil à travers l'éther peut amener l'appareil à se contracter le long de sa longueur dans la direction du mouvement, et il suppose en outre, que la variable de temps pour les systèmes en mouvement doit également être modifiée en conséquence (" heure locale "), qui a conduit à la formulation de la transformation de Lorentz. Bas?? sur La théorie de l'éther de Lorentz, Henri Poincaré (1900) a montré que cette heure locale (au premier ordre en v / c) est indiquée par des horloges en mouvement dans l'éther, qui sont synchronisées dans l'hypothèse de la vitesse de la lumière constante. En 1904, il a spéculé que la vitesse de la lumière pourrait être une limitation de vitesse dans la dynamique, à condition que les hypothèses de la théorie de Lorentz sont tous confirmés. En 1905, Poincaré a la théorie de l'éther de Lorentz en plein accord avec l'observation principe de relativit??.
Relativit?? restreinte
En 1905, Einstein a postulé dès le départ que la vitesse de la lumière dans le vide, mesurée par un observateur non-accélération, est indépendant du mouvement de la source ou de l'observateur. L'utilisation de ce et le principe de la relativité comme une base, il provient de la théorie de la relativité , dans lequel la vitesse de la lumière dans le vide c présenté comme une constante fondamentale, apparaissant aussi dans des contextes non liés à la lumière. Cela a rendu le concept de l'éther stationnaire (à laquelle Lorentz et Poincaré adhéraient encore) inutile et a révolutionné les concepts d'espace et de temps.
Une précision accrue decet redéfinition du mètre
Dans la seconde moitié de l'beaucoup de progrès du 20ème siècle a été faite en augmentant la précision des mesures de la vitesse de la lumière, d'abord par des techniques de résonance de la cavité et plus tard par des techniques de l'interféromètre laser. En 1972, en utilisant la dernière méthode et la définition de 1960 du compteur en termes d'une ligne spectrale particulière de krypton-86, un groupe au NBS dans Boulder, Colorado a déterminé la vitesse de la lumière dans le vide pour être c = 299,792,456.2 ± 1,1 m / s . Ce fut 100 fois moins incertain que la valeur précédemment accepté. L'incertitude reste était principalement liée à la définition du mètre. Depuis des expériences similaires ont trouvé des résultats comparables pour c , la 15e Conférence Générale des Poids et Mesures (CGPM) en 1975 a recommandé d'utiliser la valeur 299 792 458 m / s pour la vitesse de la lumière.
En 1983, la 17 e CGPM redéfinit le mètre ainsi, "Le mètre est la longueur du trajet parcouru par la lumière dans le vide pendant un intervalle de temps de 1/299 792 458 de seconde." Du fait de cette définition, la valeur de la vitesse de la lumière dans le vide est exactement 299 792 458 m / s et est devenue une constante définie dans le système d'unités SI. Amélioration des techniques expérimentales ne modifient pas la valeur de la vitesse de la lumière en unités SI, mais au lieu de permettre une réalisation plus précise de l'appareil.
