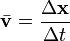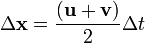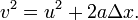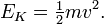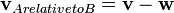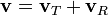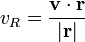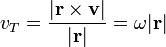Vitesse

Contexte des ??coles Wikip??dia

Arrangeant une s??lection Wikipedia pour les ??coles dans le monde en d??veloppement sans internet ??tait une initiative de SOS Enfants. Avec enfants SOS vous pouvez choisir de parrainer des enfants dans plus de cent pays

En physique , la vitesse est d??finie comme le taux de variation de la position. Il se agit d'un vecteur quantit?? physique; la fois la vitesse et la direction sont tenus de le d??finir. Dans le SI syst??me (m??trique), elle est mesur??e en m??tres par seconde: (m / s) ou ms ^-1. Le scalaire valeur absolue ( amplitude) de la vitesse est vitesse. Par exemple, "5 m??tres par seconde" est un scalaire et pas un vecteur, tandis que les ??cinq m??tres par seconde l'est" est un vecteur. La vitesse moyenne v d'un objet se d??pla??ant ?? travers un d??placement $(\ Delta \ mathbf {x})$ pendant un intervalle de temps $(\ Delta t)$ est d??crit par la formule:

$\ Bar {\ mathbf {v}} = \ frac {\ Delta \ mathbf {x}} {\ Delta t}$

Le taux de changement de vitesse est appel?? acc??l??ration .

??quation du mouvement

L'instant vecteur vitesse v d'un objet qui a des positions x (t) ?? l'instant t et x (t + 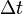${\ Delta t}$ ) Au temps t + 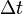${\ Delta t}$ , Peut ??tre calcul?? comme la d??riv??e de la position:

$\ Mathbf {v} = \ lim _ {\ Delta t \ 0} {{\ mathbf {x} (t + \ Delta t) - \ mathbf {x} (t)} \ over \ Delta t} = {\ mathrm { d} \ mathbf {x} \ over \ mathrm {d} t}$

L'??quation de la vitesse d'un objet peut ??tre obtenu en prenant math??matiquement l' int??grale de l'??quation pour son acc??l??ration d??but d'une certaine p??riode de temps initiale 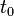$t_0$ ?? un certain moment plus tard $t_n$ .

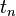La vitesse finale v d'un objet qui commence avec la vitesse u et acc??l??re ensuite ?? une acc??l??ration constante pendant une p??riode de temps $(\ Delta t)$ est:

$\ Mathbf {v} = \ mathbf {u} + \ mathbf {a} \ Delta t$

La vitesse moyenne d'un objet subissant constante acc??l??ration est 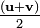$\ Begin {matrix} \ frac {(\ mathbf {u} + \ mathbf {v})} {2} \; \ End {matrix}$ , O?? u est la vitesse initiale et v est la vitesse finale. Pour trouver le d??placement, x, d'un tel objet acc??l??ration pendant un intervalle de temps, $\ Delta t$ , Puis:

$\ Delta \ mathbf {x} = \ frac {(\ mathbf {u} + \ mathbf {v})} {2} \ Delta t$

Lorsque seule la vitesse initiale de l'objet est connue, l'expression,

$\ Delta \ mathbf {x} = \ mathbf {u} \ Delta t + \ frac {1} {2} \ mathbf {a} \ Delta t ^ 2,$

peut ??tre utilis??.

Cela peut ??tre ??tendu pour donner la position ?? tout instant t de la mani??re suivante:

$\ Mathbf {x} (t) = \ mathbf {x} (0) + \ Delta \ mathbf {x} = \ mathbf {x} (0) + \ mathbf {u} \ Delta t + \ frac {1} { 2} \ mathbf {a} \ Delta t ^ 2,$

Ces ??quations de base pour vitesse finale et le d??placement peuvent ??tre combin??s pour former une ??quation qui est ind??pendante du temps, ??galement connus sous le nom L'??quation de Torricelli:

$v ^ 2 = u ^ 2 + 2a \ Delta x. \,$

Les ??quations ci-dessus sont valables pour les deux la m??canique newtonienne et la relativit?? restreinte . Lorsque la m??canique newtonienne et la relativit?? restreinte est diff??rent dans la fa??on dont diff??rents observateurs d??crire la m??me situation. En particulier, dans la m??canique newtonienne, tous les observateurs se accordent sur la valeur de t et les r??gles de transformation pour la position de cr??er une situation dans laquelle tous les observateurs non acc??l??rateur d??criraient l'acc??l??ration d'un objet avec les m??mes valeurs. Ni est vrai pour la relativit?? restreinte. En d'autres termes uniquement vitesse relative peut ??tre calcul??e.

Dans la m??canique newtonienne, l' ??nergie cin??tique ( l'??nergie du mouvement), 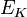$E_ {K}$ , D'un objet en mouvement est lin??aire ?? la fois sa masse par le carr?? de sa vitesse:

$E_ {K} = \ begin {matrix} \ frac {1} {2} \ end {matrix} mv ^ 2.$

L'??nergie cin??tique est un quantit?? scalaire.

Vitesse de lib??ration est la vitesse minimum un organisme doit avoir pour sortir du champ gravitationnel de la terre. Pour ??chapper ?? champ gravitationnel de la terre un objet doit avoir une plus grande ??nergie cin??tique que son ??nergie potentielle gravitationnelle. La valeur de la vitesse de lib??ration de la Terre est d'environ 11 100 m / s

Vitesse relative

Vitesse relative est une mesure de la vitesse entre deux objets que d??termin??e dans un seul syst??me de coordonn??es. Vitesse relative est fondamentale ?? la fois dans la physique classique et moderne, puisque de nombreux syst??mes en physique accord avec le mouvement relatif de deux ou plusieurs particules. En m??canique newtonienne, la vitesse relative est ind??pendante de l'image de r??f??rence inertielle choisi. Ce ne est pas plus le cas avec la relativit?? restreinte dans laquelle les vitesses d??pendent du choix du cadre de r??f??rence.

Si un objet A se d??place avec une vitesse vecteur v et un objet B avec le vecteur de vitesse w, alors la vitesse de l'objet A par rapport ?? l'objet B est d??finie comme la diff??rence entre les deux vecteurs de vitesse:

$\ Mathbf {v} _ {Arelative toB} = \ mathbf {v} - \ mathbf {w}$

De m??me, la vitesse relative de l'objet B se d??pla??ant ?? la vitesse w, par rapport ?? l'objet A se d??pla??ant ?? la vitesse v est:

$\ Mathbf {v} _ {b Relatif Toa} = \ mathbf {w} - \ mathbf {v}$

Habituellement, le rep??re inertiel est choisi dans lequel la derni??re des deux objets mentionn??s ci est en repos.

Vitesses scalaires

Dans le cas unidimensionnel, les vitesses sont scalaires et l'??quation est soit:

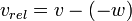$v_ {} rel = v - (-w)$ , Si les deux objets se d??placent dans des directions oppos??es, ou:

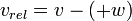$v_ {} rel = v - (+ w)$ , Si les deux objets se d??placent dans la m??me direction.

Les coordonn??es polaires

En coordonn??es polaires , une vitesse ?? deux dimensions est d??crite par une vitesse radiale, d??finie comme la composante de vitesse ??loigne ou se rapproche de l'origine (aussi connu comme vitesse effective), et une vitesse angulaire , qui est le taux de rotation autour de l' origine (avec des quantit??s positives repr??sentant sens anti-horaire et les quantit??s n??gatives repr??sentant la rotation dans le sens horaire, dans un syst??me de coordonn??es droitier).

Les vitesses angulaires et radiales peuvent ??tre obtenus ?? partir des vecteurs de d??placement et la vitesse cart??siennes par la d??composition du vecteur de vitesse dans radiales et transversales composants. Le vitesse transversale est la composante de vitesse le long d'un cercle centr?? ?? l'origine.

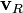$\ Mathbf {v} = \ mathbf {v} _T + \ mathbf {v} _R$

o??

$\ Mathbf {v} _T$ est la vitesse transverse

$\ Mathbf {v} _R$ est la vitesse radiale

L'amplitude de la vitesse radiale est le produit scalaire du vecteur vitesse et le vecteur unitaire dans la direction du d??placement.

$U_r = \ frac {\ mathbf {v} \ cdot \ mathbf {r}} {\ left | \ mathbf {r} \ right |}$

o??

$\ Mathbf {r}$ est le d??placement

L'amplitude de la vitesse transversale est celle du produit vectoriel du vecteur unitaire dans la direction du d??placement et le vecteur vitesse. Ce est ??galement le produit de la vitesse angulaire ( 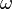$\ Omega$ ) Et l'amplitude du d??placement.

$v_T = \ frac {| \ mathbf {r} \ times \ mathbf {v} |} {| \ mathbf {r} |} = \ omega | \ mathbf {r} |$

tel que

$\ Omega = \ frac {| \ mathbf {r} \ times \ mathbf {v} |} {| \ mathbf {r} | ^ 2}$

Le moment cin??tique sous forme scalaire est la masse multipli??e par la distance ?? l'??poque d'origine, la vitesse transversale, ou de mani??re ??quivalente, la masse multipli??e par la distance au carr?? fois la vitesse angulaire. La convention de signe de moment angulaire est la m??me que celle de la vitesse angulaire.

$L = mrv_T = mr ^ 2 \ omega \,$

o??

$m \,$ est la masse

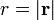
$r = | \ mathbf {r} |$

Si les forces sont dans la direction radiale avec seulement une d??pendance inverse carr??, comme dans le cas d'un gravitationnelle orbite, le moment angulaire est constante, et la vitesse transversale est inversement proportionnelle ?? la distance, la vitesse angulaire est inversement proportionnelle ?? la distance au carr??, et la vitesse ?? laquelle zone est balay??e est constante. Ces relations sont appel??es Lois de Kepler

R??cup??r?? ?? partir de " http://en.wikipedia.org/w/index.php?title=Velocity&oldid=207711794 "