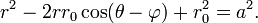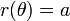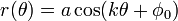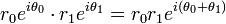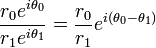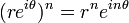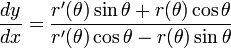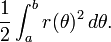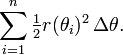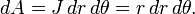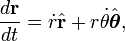Syst??me de coordonn??es polaires
Saviez-vous ...
SOS Enfants a fait cette s??lection Wikipedia aux c??t??s d'autres ??coles des ressources . Tous les enfants disponibles pour le parrainage de SOS Enfants des enfants sont pris en charge dans une maison de famille pr??s de la charit??. Lire la suite ...

En math??matiques , le syst??me de coordonn??es polaires est un bidimensionnel syst??me dans lequel chaque coordonn??e point situ?? sur un plan est d??termin??e par un angle et une distance de . Le syst??me de coordonn??es polaires est particuli??rement utile dans les situations o?? la relation entre deux points est la plus facile ?? exprimer en termes de distance et les angles; dans le plus familier cart??sienne syst??me ou coordonn??es rectangulaires, une telle relation ne peut ??tre trouv??e par le biais trigonom??triques formules.
Comme le syst??me de coordonn??es est ?? deux dimensions, chaque point est d??termin??e par deux coordonn??es polaires: la coordonn??e radiale et la coordonn??e angulaire. La coordonn??e radiale (g??n??ralement not??e  ) D??signe la distance du point ?? partir d'un point central connu sous le p??le (??quivalent ?? l'origine dans le syst??me cart??sien). La coordonn??e angulaire (??galement connu comme l'angle polaire ou la angle d'azimut, et g??n??ralement d??sign?? par θ ou
) D??signe la distance du point ?? partir d'un point central connu sous le p??le (??quivalent ?? l'origine dans le syst??me cart??sien). La coordonn??e angulaire (??galement connu comme l'angle polaire ou la angle d'azimut, et g??n??ralement d??sign?? par θ ou 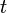 ) D??signe le positif ou dans le sens antihoraire (sens antihoraire) angle n??cessaire pour atteindre le point de la 0 ?? ray ou axe polaire (ce qui ??quivaut ?? la borne positive axe x dans le plan cart??sien).
) D??signe le positif ou dans le sens antihoraire (sens antihoraire) angle n??cessaire pour atteindre le point de la 0 ?? ray ou axe polaire (ce qui ??quivaut ?? la borne positive axe x dans le plan cart??sien).
Histoire
Les concepts d'angle et le rayon ??taient d??j?? utilis??es par les peuples anciens du 1er mill??naire BCE. Le astronome Hipparque (190-120 BCE) a cr???? un tableau de fonctions accords donnant la longueur de la corde pour chaque angle, et il ya des r??f??rences ?? son aide de coordonn??es polaires dans l'??tablissement de positions stellaires. Dans Des spirales, Archim??de d??crit la Spirale d'Archim??de, d'une fonction dont le rayon d??pend de l'angle. Le travail grec, cependant, ne se ??tend pas ?? un syst??me de coordonn??es compl??te.
Il ya diff??rents comptes de l'introduction de coordonn??es polaires dans le cadre d'un syst??me formel de coordonn??es. L'histoire compl??te de l'objet est d??crit dans Professeur ?? Harvard L'origine de Julian Lowell Coolidge des coordonn??es polaires. Gr??goire de Saint-Vincent-et- Bonaventura Cavalieri introduit ind??pendamment les concepts dans le milieu du XVIIe si??cle. Saint-Vincent a ??crit sur eux en priv?? en 1625 et publi?? son travail en 1647, tandis que Cavalieri a publi?? son en 1635 avec une version corrig??e apparaissant en 1653. Cavalieri abord utilis?? coordonn??es polaires pour r??soudre un probl??me li?? ?? la zone dans un Spirale d'Archim??de. Blaise Pascal ensuite utilis?? pour calculer les coordonn??es polaires de la longueur arcs paraboliques.
En Fluxion (??crit 1671, publi?? 1736), Sir Isaac Newton a examin?? les transformations entre coordonn??es polaires, qu'il d??nomm?? le "septi??me mani??re; Pour Spirales", et neuf autres syst??mes de coordonn??es. Dans la revue Acta Eruditorum (1691), Jacob Bernoulli utilis?? un syst??me avec un point sur une ligne, appelle le p??le et l'axe polaire respectivement. Coordonn??es ??t?? d??fini par la distance entre le p??le et l'angle de l'axe polaire. Le travail de Bernoulli ??tendu ?? trouver le rayon de courbure des courbes exprim??es dans ces coordonn??es.
Les coordonn??es polaires terme r??elle a ??t?? attribu??e ?? Gregorio Fontana et a ??t?? utilis?? par les ??crivains italiens du 18e si??cle. Le terme est apparu dans Anglais en 1816 traduction de George Peacock Lacroix calcul diff??rentiel et int??gral. Alexis Clairaut a ??t?? le premier ?? penser de coordonn??es polaires en trois dimensions, et Leonhard Euler ??tait le premier ?? r??ellement d??velopper.
Tracer des points en coordonn??es polaires

Chaque point dans le syst??me de coordonn??es polaires peut ??tre d??crite avec les deux coordonn??es polaires, qui sont g??n??ralement appel??s  (La coordonn??e radiale) et θ (la coordonn??e angulaire, angle polaire, ou angle d'azimut, parfois repr??sent?? comme φ ou
(La coordonn??e radiale) et θ (la coordonn??e angulaire, angle polaire, ou angle d'azimut, parfois repr??sent?? comme φ ou 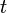 ). Le
). Le  coordonner repr??sente la distance radiale ?? partir du poteau, et la coordination θ repr??sente l'angle de 0 ?? vers la gauche (sens antihoraire) rayon (parfois appel?? axe polaire), connu sous l'axe des x positif sur le plan cart??sien .
coordonner repr??sente la distance radiale ?? partir du poteau, et la coordination θ repr??sente l'angle de 0 ?? vers la gauche (sens antihoraire) rayon (parfois appel?? axe polaire), connu sous l'axe des x positif sur le plan cart??sien .
Par exemple, les coordonn??es polaires (3, 60 ??) serait trac??e en un point 3 unit??s du p??le sur le rayon de 60 ??. Les coordonn??es (-3, 240 ??) seront ??galement trac??es ?? ce moment parce que la distance radiale n??gative est mesur??e comme une distance positive sur le rayon oppos?? (le rayon r??fl??chi sur l'origine, qui diff??re du rayon initial de 180 ??).
Un aspect important du syst??me de coordonn??es polaires, pas pr??sent dans le syst??me de coordonn??es cart??siennes, ce est que d'un seul point peut ??tre exprim?? avec un nombre infini de coordonn??es diff??rents. En effet, ne importe quel nombre de r??volutions multiples peut ??tre r??alis?? autour du p??le central sans affecter la position r??elle du point trac??. En g??n??ral, le point (  , Θ) peut ??tre repr??sent?? par (
, Θ) peut ??tre repr??sent?? par (  , Θ ??
, Θ ??  ?? 360 ??) ou (-
?? 360 ??) ou (-  , Θ ?? (2
, Θ ?? (2  + 1) 180 ??), o??
+ 1) 180 ??), o??  est ne importe quel nombre entier .
est ne importe quel nombre entier .
Les coordonn??es arbitraires (0, θ) sont classiquement utilis??es pour repr??senter le p??le, que quel que soit le θ coordonner, un point de rayon 0 sera toujours sur le poteau. Pour obtenir une repr??sentation unique d'un point, il est habituel de limiter  pour les num??ros non-n??gatifs
pour les num??ros non-n??gatifs  ≥ 0 et θ ?? la intervalle [0, 360 ??) ou (-180 ??, 180 ??] (ou, en radians, [0, 2π) ou (-π, π]).
≥ 0 et θ ?? la intervalle [0, 360 ??) ou (-180 ??, 180 ??] (ou, en radians, [0, 2π) ou (-π, π]).
Angles en notation polaire sont g??n??ralement exprim??es en degr??s ou en radians , en utilisant les deux conversion π rad = 360 ??. Le choix d??pend en grande partie du contexte. Les applications de navigation utilisent mesure en degr??s, tandis que certains physique applications (m??canique sp??cifiquement rotation) et presque toute la litt??rature math??matique sur le calcul utilisent radians.
Conversion entre coordonn??es polaires et cart??siennes

Les deux coordonn??es polaires  et θ peuvent ??tre convertis en les coordonn??es cart??siennes
et θ peuvent ??tre convertis en les coordonn??es cart??siennes  et
et 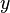 ?? l'aide de la fonction trigonom??trique sinus et le cosinus:
?? l'aide de la fonction trigonom??trique sinus et le cosinus:
tandis que les deux coordonn??es cart??siennes  et
et 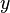 peuvent ??tre convertis en coordonn??es polaires
peuvent ??tre convertis en coordonn??es polaires  par
par
 (Par une simple application de la th??or??me de Pythagore ).
(Par une simple application de la th??or??me de Pythagore ).
Pour d??terminer l'angle θ de coordonn??es, les deux id??es suivantes doivent ??tre envisag??es:
- Pour
 = 0, θ peut ??tre r??gl?? sur toute valeur r??elle .
= 0, θ peut ??tre r??gl?? sur toute valeur r??elle . - Pour
 ≠ 0, pour obtenir une repr??sentation unique pour θ, elle doit ??tre limit??e ?? un intervalle de taille 2π. Choix classiques pour un tel intervalle sont [0, 2π) et (-π, π].
≠ 0, pour obtenir une repr??sentation unique pour θ, elle doit ??tre limit??e ?? un intervalle de taille 2π. Choix classiques pour un tel intervalle sont [0, 2π) et (-π, π].
Pour obtenir θ dans l'intervalle [0, 2π), ce qui suit peut ??tre utilis?? (  d??signe l'inverse de la tangente fonction):
d??signe l'inverse de la tangente fonction):
Pour obtenir θ dans l'intervalle (-π, π], celui-ci peut ??tre utilis??:
On peut ??viter d'avoir ?? garder une trace des signes de num??rateur et d??nominateur par l'utilisation de la atan2 fonction, qui a des arguments distincts pour le num??rateur et le d??nominateur.
??quations polaires
L'??quation d??finissant une courbe alg??brique exprim??e en coordonn??es polaires est connue comme une ??quation polaire. Dans de nombreux cas, une telle ??quation peut simplement ??tre sp??cifi?? en d??finissant  en tant que fonction de θ. La courbe obtenue est alors constitu?? de points de la forme (
en tant que fonction de θ. La courbe obtenue est alors constitu?? de points de la forme (  (Θ), θ), et peut ??tre consid??r??e comme la graphe de la fonction polaire
(Θ), θ), et peut ??tre consid??r??e comme la graphe de la fonction polaire  .
.
Diff??rentes formes de sym??trie peuvent ??tre d??duites ?? partir de l'??quation d'une fonction polaire  . Si
. Si  (-θ) =
(-θ) =  (Θ) de la courbe sera sym??trique par rapport au rayon horizontal (0 ?? / 180 ??), si
(Θ) de la courbe sera sym??trique par rapport au rayon horizontal (0 ?? / 180 ??), si  (Π-θ) =
(Π-θ) =  (Θ), il sera sym??trique par rapport ?? la (90 ?? / 270 ??) rayon vertical, et si
(Θ), il sera sym??trique par rapport ?? la (90 ?? / 270 ??) rayon vertical, et si  (Θ-α ??) =
(Θ-α ??) =  (Θ), il sera α ?? ?? sym??trie de r??volution dans le sens antihoraire autour du p??le.
(Θ), il sera α ?? ?? sym??trie de r??volution dans le sens antihoraire autour du p??le.
En raison de la nature circulaire du syst??me de coordonn??es polaires, de nombreuses courbes peuvent ??tre d??crites par une ??quation polaire plut??t simple, tandis que leur forme cart??sienne est beaucoup plus complexe. Parmi les plus connus de ces courbes sont les Polar Rose, Spirale d'Archim??de, lemniscate, lima??on, et cardio??de.
Pour le cercle, la ligne et rose polaire ci-dessous, il est entendu qu'il n'y a pas de restrictions sur le domaine et de la courbe.
Cercle

 (Θ) = 1
(Θ) = 1 L'??quation g??n??rale pour un cercle avec un centre au (  0, φ) et le rayon
0, φ) et le rayon  est
est
Cela peut ??tre simplifi??e de diverses mani??res, afin de se conformer ?? des cas plus particuliers, comme l'??quation
pour un cercle avec un centre au niveau du p??le et de rayon  .
.
Ligne
Lignes radiales (ceux fonctionnant par le p??le) sont repr??sent??s par l'??quation
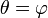 ,
,
o?? φ est l'angle d'??l??vation de la ligne; ce est-?? φ = arctan 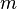 o??
o?? 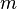 est le pente de la droite dans le syst??me de coordonn??es cart??siennes. La ligne non radial qui traverse les = φ de la ligne radiale perpendiculairement au point (
est le pente de la droite dans le syst??me de coordonn??es cart??siennes. La ligne non radial qui traverse les = φ de la ligne radiale perpendiculairement au point (  0, φ) a l'??quation
0, φ) a l'??quation
Polar Rose

 (Θ) = 2 sin 4θ
(Θ) = 2 sin 4θ Un rose polaire est une courbe math??matique c??l??bre qui ressemble ?? une fleur p??tales, et qui peut ??tre exprim?? en ??quation polaire simple,
pour ne importe quelle constante 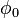 (Y compris 0). Si k est un nombre entier, ces ??quations produira un -petalled k si k est augment?? impair, ou 2 k -petalled augment?? si k est pair. Si k est rationnel mais pas un nombre entier, une forme de rose comme peut former, mais avec des p??tales qui se chevauchent. On notera que ces ??quations d??finissent jamais une rose avec 2, 6, 10, 14, etc. p??tales. Le une variable repr??sentant la longueur des p??tales de la rose.
(Y compris 0). Si k est un nombre entier, ces ??quations produira un -petalled k si k est augment?? impair, ou 2 k -petalled augment?? si k est pair. Si k est rationnel mais pas un nombre entier, une forme de rose comme peut former, mais avec des p??tales qui se chevauchent. On notera que ces ??quations d??finissent jamais une rose avec 2, 6, 10, 14, etc. p??tales. Le une variable repr??sentant la longueur des p??tales de la rose.
Spirale d'Archim??de

Le Spirale d'Archim??de est une spirale c??l??bre qui a ??t?? d??couvert par Archim??de , qui peut ??galement ??tre exprim?? en ??quation polaire simple. Elle est repr??sent??e par l'??quation
Modification du param??tre a tournera la spirale, tandis que b contr??le la distance entre les bras, qui, pour une spirale donn??e est toujours constante. La spirale d'Archim??de a deux bras, l'un pour θ> 0 et une pour θ <0. Les deux bras sont reli??s en douceur au niveau du p??le. Prenant l'image miroir d'un bras ?? travers la ligne de 90 ?? ?? / 270 donnera l'autre bras. Cette courbe est remarquable comme l'une des premi??res courbes, apr??s les sections coniques , ??tre d??crit dans un trait?? de math??matiques, et comme ??tant un excellent exemple d'une courbe qui est le mieux d??fini par une ??quation polaire.
Sections coniques
Une section conique avec un seul objectif sur le poteau et l'autre quelque part sur le rayon 0 ?? (de sorte que de la conique grand axe se ??tend le long de l'axe polaire) est donn??e par:
o?? e est la excentricit?? et  est le semi-latus rectum (la distance perpendiculaire ?? un foyer de l'axe majeur de la courbe). Si e> 1, cette ??quation d??finit une hyperbole; si e = 1, on d??finit un parabole; et si E <1, il d??finit une ellipse . Le cas sp??cial e = 0 des derniers r??sultats dans un cercle de rayon
est le semi-latus rectum (la distance perpendiculaire ?? un foyer de l'axe majeur de la courbe). Si e> 1, cette ??quation d??finit une hyperbole; si e = 1, on d??finit un parabole; et si E <1, il d??finit une ellipse . Le cas sp??cial e = 0 des derniers r??sultats dans un cercle de rayon  .
.
Les nombres complexes
Chaque nombre complexe peut ??tre repr??sent?? par un point dans le plan complexe , et peut donc ??tre exprim??e soit en sp??cifiant les coordonn??es cart??siennes est le point (appel??es forme rectangulaire ou cart??sienne) ou les coordonn??es polaires de la virgule (appel??e forme polaire). Le nombre complexe z peut ??tre repr??sent?? sous forme rectangulaire
o?? i est l' unit?? imaginaire , ou peut alternativement ??tre ??crit sous forme polaire (via les formules de conversion donn??s ci-dessus ) que
et ?? partir de l?? que
o?? e est Le nombre d'Euler, qui sont ??quivalentes, comme indiqu?? par La formule d'Euler. (Notez que cette formule, comme tous ceux qui impliquent des angles exponentielles, suppose que l'angle θ est exprim?? en radians). Pour une conversion entre les formes rectangulaires et polaires d'un nombre complexe, les formules de conversion indiqu??es ci-dessus peuvent ??tre utilis??s.
Pour les op??rations de multiplication , division et exponentiation des nombres complexes, il est g??n??ralement beaucoup plus simple de travailler avec des nombres complexes exprim??es sous forme polaire plut??t que la forme rectangulaire. Des lois de la exponentiation:
- Multiplication:
- Division:
- Exponentiation ( La formule de De Moivre):
Calcul
Calcul peut ??tre appliqu??e ?? des ??quations exprim??es en coordonn??es polaires.
Le θ coordonn??e angulaire est exprim?? en radians au long de cette section, qui est le choix classique lorsque vous faites le calcul.
Calcul diff??rentiel
Nous avons les formules suivantes:
Pour trouver la pente cart??sienne de la tangente ?? une courbe r polaire (θ) ?? un moment donn??, la courbe est d'abord exprim??e comme un syst??me de ??quations param??triques.
Diff??rencier les deux ??quations par rapport aux rendements θ
La division de la seconde ??quation par les premiers rendements cart??sien la pente de la tangente ?? la courbe au point (r, r (θ)):
Calcul int??gral
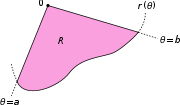
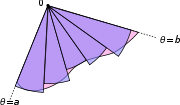
Soit R d??signent la r??gion d??limit??e par une courbe r (θ) et les rayons θ = a et θ = b, o?? 0 <b - un <2π. Ensuite, la zone de R est
Ce r??sultat peut ??tre trouv?? comme suit. En premier lieu, l'intervalle [a, b] est divis??e en n sous-intervalles, o?? n est un nombre entier positif arbitraire. Ainsi Δθ, la longueur de chaque sous-intervalle, est ??gal ?? b - a (la longueur totale de l'intervalle), divis??e par n, le nombre de sous-intervalles. Pour chaque sous-intervalle i = 1, 2, ..., n, permettez θ i le point m??dian de la sous-intervalle, et de construire un secteur avec le centre au p??le, rayon r (θ i), angle central Δθ et longueur d'arc  . La superficie de chaque secteur construit est donc ??gale ??
. La superficie de chaque secteur construit est donc ??gale ??  . Par cons??quent, la surface totale de l'ensemble des secteurs est
. Par cons??quent, la surface totale de l'ensemble des secteurs est
Comme le nombre de sous-intervalles n est augment??e, le rapprochement de la zone continue de se am??liorer. Dans la limite N → ∞, la somme devient le Somme de Riemann pour l'int??grale ci-dessus.
G??n??ralisation
Utilisation de coordonn??es cart??siennes , un ??l??ment de la zone infinit??simale peut ??tre calcul??e comme dA = dx dy. Le r??gle de substitution pour les int??grales multiples indique que, lors de l'utilisation d'autres coordonn??es, les D??terminant jacobien de la formule de coordonner de conversion doit ??tre consid??r??:
Par cons??quent, un ??l??ment de surface en coordonn??es polaires peut se ??crire
Maintenant, une fonction qui est donn?? en coordonn??es polaires peut ??tre int??gr?? comme suit:
Ici, R est la m??me r??gion que pr??c??demment, ?? savoir, la r??gion d??limit??e par une courbe r (θ) et les rayons θ = θ a et b =.
La formule pour le domaine de la R mentionn?? ci-dessus est r??cup??r?? en prenant f identiquement ??gale ?? 1. Une application plus surprenant de ce r??sultat donne le Int??grale de Gauss
Calcul vectoriel
Vecteur calcul peut ??galement ??tre appliqu??e ?? des coordonn??es polaires. Laisser  le vecteur de position
le vecteur de position  , O?? r et
, O?? r et  en fonction du temps t,
en fonction du temps t,  ??tre un vecteur unitaire dans la direction
??tre un vecteur unitaire dans la direction  et
et 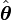 ??tre un vecteur unitaire perpendiculaire ??
??tre un vecteur unitaire perpendiculaire ??  . Les premi??re et seconde positions sont des d??riv??s de
. Les premi??re et seconde positions sont des d??riv??s de
Trois dimensions
Le syst??me de coordonn??es polaires est ??tendu en trois dimensions avec deux syst??mes de coordonn??es diff??rents syst??mes de coordonn??es, la cylindrique et sph??rique, deux qui comprennent deux dimensions ou coordonn??es polaires planes comme un sous-ensemble. Essentiellement, le syst??me de coordonn??es cylindrique se ??tend coordonn??es polaires par l'ajout d'une distance suppl??mentaire de coordonn??es, tandis que le syst??me sph??rique ajoute un suppl??ment de place coordonn??e angulaire.
Coordonn??es cylindriques
Le syst??me de coordonn??es cylindrique est un syst??me de coordonn??es qui se ??tend essentiellement ?? deux dimensions le syst??me de coordonn??es polaires par l'ajout d'une troisi??me coordonn??e ?? mesurer la hauteur d'un point au-dessus du plan, similaire ?? la mani??re dont le syst??me de coordonn??es cart??siennes se ??tend dans trois dimensions. La troisi??me coordonn??e est habituellement not??e h, rendant les trois coordonn??es cylindriques (r, θ, h).
Les trois coordonn??es cylindriques peuvent ??tre converties en coordonn??es cart??siennes par:
Coordonn??es sph??riques
Les coordonn??es polaires peuvent ??galement ??tre ??tendues en trois dimensions en utilisant les coordonn??es (ρ, φ, θ), o?? ρ est la distance de l'origine, φ est l'angle de l'axe z (appel?? colatitude ou z??nith et mesur??e 0-180 ??) et θ est l'angle de l'axe x (comme dans les coordonn??es polaires). Ce syst??me de coordonn??es, appel?? le syst??me de coordonn??es sph??riques, est similaire ?? la latitude et Syst??me de longitude utilis?? pour la Terre, ?? l'origine dans le centre de la Terre, la latitude de δ ??tant le compl??ment de φ, d??termin??e par δ = 90 ?? - φ, la longitude et l ??tant mesur??e par l = θ - 180 ??.
Les trois coordonn??es sph??riques sont converties en coordonn??es cart??siennes par:
Applications
Les coordonn??es polaires sont ?? deux dimensions et par cons??quent ils peuvent ??tre utilis??s que lorsque la position des points se trouvent sur un seul plan ?? deux dimensions. Ils sont les plus appropri??es dans un contexte o?? le ph??nom??ne ??tant consid??r?? est intrins??quement li??e ?? la direction et la longueur d'un point central. Par exemple, les exemples ci-dessus montrent comment des ??quations polaires ??l??mentaires suffisent ?? d??finir des courbes - comme la spirale d'Archim??de - dont l'??quation dans le syst??me de coordonn??es cart??siennes seraient beaucoup plus complexe. En outre, de nombreux syst??mes physiques - tels que ceux concern??s par les corps en mouvement autour d'un point central ou ?? des ph??nom??nes provenant d'un point central - sont plus simple et plus intuitive pour mod??liser en coordonn??es polaires. La motivation initiale pour l'introduction du syst??me polaire ??tait l'??tude de circulaire et mouvement orbital.
Les coordonn??es polaires sont souvent utilis??s dans la navigation, la destination ou la direction de Voyage peuvent ??tre donn??s comme un angle et la distance de l'objet ?? l'??tude. Par exemple, les a??ronefs utilisent une version l??g??rement modifi??e des coordonn??es polaires pour la navigation. Dans ce syst??me, celui g??n??ralement utilis?? pour toute sorte de navigation, le rayon de 0 ?? est g??n??ralement appel??e la position 360, et les angles continue dans un le sens horaire, plut??t que dans le sens antihoraire, comme dans le syst??me math??matique. Rubrique 360 correspond ?? nord magn??tique, tout en rubriques 90, 180 et 270 correspondent ?? l'est magn??tique, le sud et ?? l'ouest, respectivement. Ainsi, un avion voyageant 5 miles nautiques ?? l'est se rendront cinq unit??s au titre 90 (lire niner-z??ro contr??le du trafic a??rien).
Mod??lisation
Syst??mes d'affichage sym??trie radiale fournir milieux naturels pour le syst??me de coordonn??es polaires, avec le point central agissant comme le p??le. Un excellent exemple de cet usage est le ??quation d'??coulement des eaux souterraines lorsqu'il est appliqu?? aux puits radialement sym??triques. Syst??mes avec un force radiale sont ??galement de bons candidats pour l'utilisation du syst??me de coordonn??es polaires. Ces syst??mes comprennent les champs gravitationnels , qui ob??issent ?? la loi de l'inverse carr??, ainsi que des syst??mes avec des sources ponctuelles, telles que antennes radio.
Radialement syst??mes asym??triques peuvent ??galement ??tre mod??lis??s avec des coordonn??es polaires. Par exemple, un du microphone motif ramassage illustre sa r??ponse proportionnelle ?? un son en provenance d'un sens donn??, et ces motifs peuvent ??tre repr??sent??s sous forme de courbes polaires. La courbe pour un microphone cardio??de standard, le microphone unidirectionnel le plus commun, peut ??tre repr??sent?? comme r = 0,5 + 0,5 p??ch?? θ.