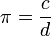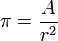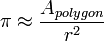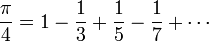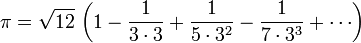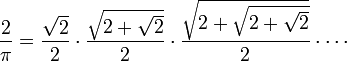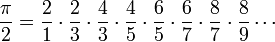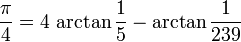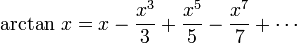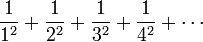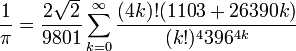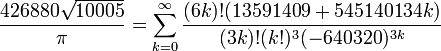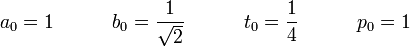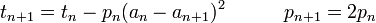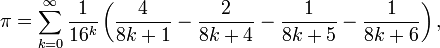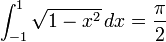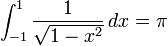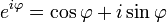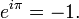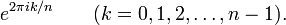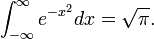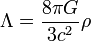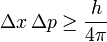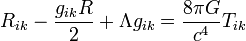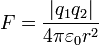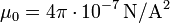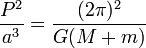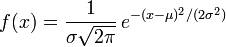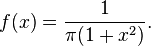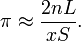Pi

Lorsque le diam??tre d'un cercle est 1, sa circonf??rence est π.

Liste des num??ros - Les nombres irrationnels ζ (3) - √2 - √3 - √5 - φ - α - e - π - δ
Binaire	11,00100100001111110110 ...
D??cimal	3,14159265358979323846 ...
Hexad??cimal	3.243F6A8885A308D31319 ...
Fraction continue	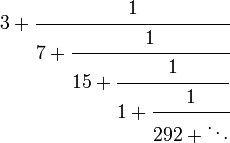Notez que cette fraction continue ne est pas p??riodique.

Pi ou π est une des plus importantes constantes math??matiques, ?? peu pr??s ??gales ?? 3,14159. Il repr??sente le rapport de tout cercle circonf??rence de son diam??tre en g??om??trie euclidienne , qui est le m??me que le rapport de la superficie d'un cercle au carr?? de son rayon. Beaucoup de formules des math??matiques, la science et l'ing??nierie impliquent π.

Ce est un nombre irrationnel , ce qui signifie qu'il ne peut pas ??tre exprim??e comme une fraction m / n, o?? m et n sont des nombres entiers . Par cons??quent son repr??sentation d??cimale ne finit jamais ou des r??p??titions. En plus d'??tre irrationnel , ce est un nombre transcendant, ce qui signifie qu'aucun ordre fini des op??rations alg??briques sur les nombres entiers (puissances, de racines, sommes, etc.) ne pourrait jamais produire. Tout au long de l'histoire des math??matiques, beaucoup d'efforts ont ??t?? faits pour π d??terminer plus pr??cis??ment et de comprendre sa nature; la fascination avec le nombre a m??me report?? dans la culture au sens large.

La lettre π grec, souvent d??fini pi en texte, a ??t?? adopt?? pour le nombre du mot grec pour le p??rim??tre "περίμετρος", probablement par William Jones en 1706, et popularis?? par Leonhard Euler quelques ann??es plus tard. La constante est parfois aussi appel??e la constante circulaire, d'Archim??de 'constante (?? ne pas confondre avec un Nombre d'Archim??de), ou Le num??ro de Ludolph.

Fundamentals

La lettre π

Minuscule π (la lettre minuscule est utilis?? pour la constante)

Le nom de la Lettre grecque π est pi, et cette orthographe est utilis??e dans contextes typographiques o?? la lettre grecque ne est pas disponible ou lorsque son utilisation pourrait ??tre probl??matique. Lorsqu'on se r??f??re ?? cette constante, le symbole π est toujours prononc?? comme "tarte" en anglais , la prononciation anglaise conventionnelle de la lettre. En grec, le nom de cette lettre est prononc?? / pi /.

Le constante est appel??e "π" parce que "π" est la premi??re lettre des grecs mots περιφέρεια (p??riph??rie) et περίμετρος (p??rim??tre), probablement ?? son utilisation dans la formule de trouver la circonf??rence, ou le p??rim??tre d'un cercle. π est Unicode caract??re U + 03C0 (" minuscule grecque pi ").

D??finition

Circonf??rence = π ?? diam??tre

En g??om??trie plane euclidienne , π est d??finie comme la rapport d'un cercle de l ' sa circonf??rence au diam??tre :

A noter que le rapport ^c / _d ne d??pend pas de la taille du cercle. Par exemple, si un cercle a deux fois le diam??tre d de l'autre cercle, il aura ??galement deux fois la circonf??rence c, en conservant le rapport ^c / _d. Cet effet est une cons??quence de la similitude de tous les milieux.

Aire du cercle = π ?? superficie de la place ombrag??e

Alternativement π peut ??tre ??galement d??fini comme le rapport d'un cercle de la zone (A) ?? la zone d'un carr?? dont le c??t?? est ??gal ?? la rayon:

La constante π peut ??tre d??finie par d'autres moyens qui permettent d'??viter les concepts de longueur de l'arc et de la zone, par exemple, que deux fois par le plus petit x positif pour ce qui cos (x) = 0. Les formules ci-dessous illustrent d'autres d??finitions (??quivalentes).

Irrationalit?? et de la transcendance

La constante π est un nombre irrationnel ; autrement dit, il ne peut pas ??tre ??crit par le rapport de deux nombres entiers . Cela a ??t?? prouv?? dans 1761 par Johann Heinrich Lambert. Au 20e si??cle, les preuves ont ??t?? trouv??es qui exigent aucune connaissance pr??alable del?? calcul int??gral. Un de ceux, en raison de Ivan Niven, est largement connu. Une preuve un peu plus t??t similaire est par Mary Cartwright.

En outre, π est ??galement transcendantale, comme cela a ??t?? prouv?? par Ferdinand von Lindemann en 1882 . Cela signifie qu'il n'y a pas polyn??me avec rationnels de coefficients qui est un π racine. Une cons??quence importante de la transcendance de π est le fait que ce ne est pas constructible. Parce que les coordonn??es de tous les points qui peuvent ??tre construits avec r??gle et au compas sont des nombres constructibles, il est impossible de la quadrature du cercle: ce est, il est impossible de construire, en utilisant r??gle et au compas seul, un carr?? dont la superficie est ??gale ?? la surface d'un cercle donn??.

Valeur num??rique

La valeur num??rique de π tronqu??e ?? 50 d??cimales est:

3,14159 26535 89793 23846 26433 83279 50288 41971 69399 37510

Voir les liens ci-dessous et ceux de la s??quence A000796 dans OEIS pour plus de chiffres.

Bien que la valeur de pi a ??t?? calcul?? ?? plus d'un billions (10 ¹²⁾ chiffres, applications ??l??mentaires, tels que le calcul de la circonf??rence d'un cercle, aura rarement besoin de plus d'une douzaine de d??cimales. Par exemple, une valeur tronqu??e ?? 39 d??cimales est suffisant pour calculer la circonf??rence de ne importe quel cercle qui se adapte dans le univers observable avec une pr??cision comparable ?? la taille d'un atome d'hydrog??ne.

π lui-m??me a une infinie d??veloppement d??cimal; parce π est un nombre irrationnel , son expansion d??cimale ne finit jamais et ne r??p??ter. Cette s??quence infinie de chiffres a math??maticiens et la??cs fascin?? aussi bien, et beaucoup d'efforts au cours des derniers si??cles a ??t?? mis en calcul plusieurs chiffres et d'enqu??ter sur les propri??t??s du nombre. Malgr?? beaucoup de travail analytique et calculs de superordinateurs qui ont d??termin?? plus de 1 billion chiffres de π, aucun mod??le simple dans les chiffres ne ont jamais ??t?? trouv??s. Chiffres de π sont disponibles sur de nombreuses pages web, et il est logiciel de calcul π ?? des milliards de chiffres sur ne importe quel ordinateur personnel .

Π calcul

π peut ??tre mesur??e de fa??on empirique en dessinant un grand cercle, puis en mesurant le diam??tre et la circonf??rence, depuis la circonf??rence d'un cercle est toujours π fois son diam??tre. Une autre approche bas??e sur la g??om??trie, en raison de Archimedes , est d'attirer un cercle imaginaire de rayon r centr?? ?? l'origine. L'aire du cercle peut ??tre approxim??e par l'inscription d'un polygone r??gulier ?? l'int??rieur du cercle, et le calcul de la superficie du polygone; les plus c??t??s du polygone a, plus l'approximation. Puis, en utilisant la relation que la zone A d'un cercle est π fois le carr?? du rayon r, π peut ??tre approch??e en utilisant:

π peut ??galement ??tre calcul?? en utilisant des m??thodes purement math??matiques. La plupart des formules utilis??es pour calculer la valeur de π ont des propri??t??s math??matiques souhaitables, mais sont difficiles ?? comprendre sans un fond dans la trigonom??trie et le calcul . Cependant, certains sont assez simples, comme cette forme de la S??rie Leibniz:

.

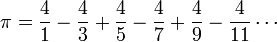Bien que cette s??rie est facile ?? ??crire et ?? calculer, il ne est pas imm??diatement ??vident pourquoi il donne π. En outre, cette s??rie converge si lentement que 300 termes ne sont pas suffisantes pour calculer correctement π ?? 2 d??cimales.

Histoire

L'histoire de π parall??le le d??veloppement des math??matiques dans son ensemble. Certains auteurs divisent les progr??s en trois p??riodes: la p??riode antique au cours de laquelle a ??t?? ??tudi??e π g??om??triquement, l'??poque classique la suite du d??veloppement du calcul en Europe autour du 17??me si??cle, et l'??ge des ordinateurs num??riques.

P??riode g??om??trique

Que le rapport de la circonf??rence au diam??tre d'un cercle est le m??me pour tous les milieux, et qu'il est un peu plus de trois, ??tait connu pour g??om??tres ??gyptienne, babylonienne, indiens et grecs anciens. Les approximations connus les plus anciens datent de 1900 autour de Colombie-Britannique; ils sont 25/8 (Babylone) et 256/81 (Egypte), ?? la fois au sein de 1% de la valeur r??elle. Le texte indien Shatapatha Brahmane donne π ≈ 339/108 que 3,139. Le Tanakh semble sugg??rer, dans le livre de Kings, que π = 3, qui est notamment pire que les autres estimations disponibles au moment de la r??daction (600 avant JC). L'interpr??tation du passage est contest??e, comme certains le croient le rapport de 3: 1. Est d'une circonf??rence ext??rieure d'un diam??tre int??rieur d'un bassin ?? paroi mince, ce qui pourrait bien ??tre un rapport pr??cis, en fonction de l'??paisseur des murs Voir: Valeur biblique de Pi.

Archim??de (287-212 avant JC) fut le premier ?? π estimer rigoureusement. Il a r??alis?? que son ampleur peut ??tre limit??e par le dessous et ci-dessus en inscrivant cercles polygones r??guliers et calculer les p??rim??tres respectifs des polygones ext??rieurs et int??rieurs de:

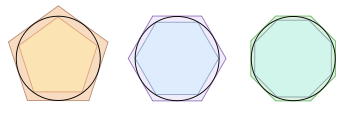
En utilisant l'??quivalent de 96 polygones-verso, il a prouv?? que 223/71 <π <22/7. Prenant la moyenne de ces valeurs donne 3,1419. Dans les si??cles suivants, la plupart d??veloppement important a eu lieu en Inde et en Chine. Autour de 480, le math??maticien chinois Zu Chongzhi donn?? le rapprochement π = 355/113, et a montr?? que 3,1415926 <π <3,1415927, qui se pr??senter comme la valeur la plus pr??cise pour π au cours des 900 prochaines ann??es.

P??riode classique

Jusqu'?? ce que le deuxi??me mill??naire, π ??tait connu ?? moins de 10 chiffres d??cimaux. La prochaine avanc??e majeure dans l'??tude de π est venu avec le d??veloppement de calcul , et en particulier la d??couverte de s??rie infinie qui, en principe permis calcul π ?? toute pr??cision souhait??e en ajoutant suffisamment nombreux termes. Autour de 1400, Madhava de Sangamagrama trouv?? le premier connu une telle s??rie:

(Maintenant connu sous le nom S??rie Leibniz depuis qu'il a ??t?? red??couvert par James Gregory et Gottfried Leibniz au 17e si??cle). Malheureusement, le taux de convergence est trop lent pour calculer le nombre de chiffres dans la pratique; environ 4000 termes doivent ??tre additionn??es pour am??liorer l'estimation d'Archim??de. Cependant, en transformant dans la s??rie

Madhava a pu calculer que π 3,14159265359, correct de 11 d??cimales. Le record a ??t?? battu en 1424 par l'astronome persan Al-Kachi, qui a d??termin?? 16 d??cimales de π.

La premi??re contribution europ??enne majeure depuis Archim??de a ??t?? faite par le math??maticien allemand Ludolph van Ceulen (1540-1610), qui a utilis?? une m??thode g??om??trique pour calculer 35 d??cimales de π. Il ??tait si fier de calcul, qui exigeait la plus grande partie de sa vie, qu'il avait les chiffres grav??s dans sa pierre tombale.

Vers la m??me ??poque, les m??thodes de calcul et la d??termination de la s??rie et des produits pour les quantit??s g??om??triques infinie ont commenc?? ?? ??merger en Europe. La premi??re repr??sentation a ??t?? la La formule de Vi??te,

trouv??e par Fran??ois Vi??te en 1593. Un autre r??sultat est c??l??bre Le produit de Wallis,

??crit par . John Wallis en 1655 Isaac Newton lui-m??me d??riv?? d'une s??rie de π et calcul??es 15 chiffres, mais il a avou?? plus tard: ??Je ai honte de vous dire de combien de chiffres que je portais ces calculs, ne ayant d'autre entreprise ?? l'??poque."

John Machin ??tait le premier ?? calculer 100 d??cimales de π, en utilisant la formule

avec

Formules de ce type, maintenant connu sous le nom Formules de Machin, ont ??t?? utilis??s pour d??finir plusieurs enregistrements successifs et sont rest??s la meilleure m??thode connue pour calculer π bien dans l'??re des ordinateurs. Un bilan remarquable a ??t?? fix?? par le prodige de calcul Zacharias Dase, qui en 1844 employait une Formule de Machin pour calculer 200 d??cimales de π dans sa t??te. La meilleure valeur ?? la fin du 19??me si??cle ??tait due ?? William Shanks, qui a pris 15 ann??es pour calculer π avec 707 chiffres, bien qu'en raison d'une erreur que la premi??re 527 ??tait correcte. (Pour ??viter de telles erreurs, modernes calculs de disques de toute nature sont souvent effectu??es deux fois, avec deux formules diff??rentes. Si les r??sultats sont les m??mes, ils sont susceptibles d'??tre correcte.)

Avanc??es th??oriques dans le 18??me si??cle ont conduit ?? des id??es sur la nature de π qui ne pourraient pas ??tre obtenus gr??ce ?? un calcul num??rique seul. Johann Heinrich Lambert prouva l'irrationalit?? de π en 1761, et Adrien-Marie Legendre se est av??r?? en 1794 que π ² est aussi irrationnel. Lorsque Leonhard Euler en 1735 r??solu la c??l??bre Probl??me de B??le - trouver la valeur exacte de

qui est π ^2/6, il a ??tabli un lien profond entre π et nombres premiers . Les deux Legendre et Leonhard Euler sp??cul?? que π pourrait ??tre transcendantale, un fait qui a ??t?? prouv?? en 1882 par Ferdinand von Lindemann.

Livre une nouvelle introduction de William Jones math??matiques de 1706 est cit?? comme le premier texte o?? le Lettre grecque π a ??t?? utilis?? pour cette constante, mais cette notation est devenue particuli??rement populaire apr??s Leonhard Euler adopt?? en 1737. Il a ??crit:

Calcul de l'??ge de l'ordinateur

L'av??nement des ordinateurs num??riques au 20??me si??cle a conduit ?? une augmentation du taux de nouveaux records de calcul π. John von Neumann utilis?? ENIAC pour calculer 2037 chiffres de π en 1949, un calcul qui a pris 70 heures. Des milliers de d??cimales suppl??mentaires ont ??t?? obtenus dans les d??cennies suivantes, avec le cap du million chiffres adopt??e en 1973. Les progr??s ne ??tait pas seulement due ?? un mat??riel plus rapide, mais aussi de nouveaux algorithmes. Un des d??veloppements les plus significatifs a ??t?? la d??couverte de la transform??e de Fourier rapide (FFT) dans les ann??es 1960, qui permet ?? des ordinateurs pour effectuer des op??rations arithm??tiques sur un tr??s grand nombre rapidement.

Au d??but du 20e si??cle, le math??maticien indien Srinivasa Ramanujan a trouv?? beaucoup de nouvelles formules pour π, certains remarquables par leur ??l??gance et la profondeur math??matique. Une de ses formules les plus c??l??bres est la s??rie

qui fournit 14 chiffres par trimestre. Les fr??res Chudnovsky utilis?? cette formule pour r??gler plusieurs dossiers informatiques π dans la fin des ann??es 1980, y compris le premier calcul de plus d'un milliard (1011196691) d??cimales en 1989. Il reste la formule de choix pour le calcul de π logiciel qui se ex??cute sur les ordinateurs personnels, par opposition ?? la superordinateurs utilis??s pour ??tablir des records modernes.

Alors que la s??rie augmentent g??n??ralement la pr??cision avec un montant fixe pour chaque terme ajout??, il existe des algorithmes it??ratifs qui multiplient le nombre de chiffres corrects ?? chaque ??tape, avec l'inconv??nient que chaque ??tape n??cessite g??n??ralement un calcul co??teux. Une perc??e a ??t?? faite en 1975, quand Richard Brent et Eugene Salamin d??couvert ind??pendamment du Brent-Salamin algorithme, qui utilise seulement arithm??tique de doubler le nombre de chiffres corrects ?? chaque ??tape. L'algorithme consiste ?? mettre en

et l'it??ration

jusqu'?? ce qu'un _n et b _n sont suffisamment proches. Puis l'estimation de π est donn?? par

.

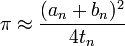En utilisant ce sch??ma, 25 it??rations suffisent pour atteindre 45 millions de d??cimales correctes. Un algorithme similaire qui multiplie par quatre la pr??cision dans chaque ??tape a ??t?? trouv?? par Jonathan et Peter Borwein. Les m??thodes ont ??t?? utilis??es par Yasumasa Kanada et l'??quipe pour d??finir la plupart des dossiers de calcul de π depuis 1980, jusqu'?? un calcul de 206 158 430 000 d??cimales de π en 1999. Le record actuel est 1.241.100.000.000 d??cimales, fix??s par Kanada et de l'??quipe en 2002. Bien que la plupart des dossiers ant??rieurs de Kanada ont ??t?? fix??s en utilisant l'algorithme Brent-Salamin, le calcul 2002 fait usage de deux formules de Machin qui ??taient plus lent, mais cruciale r??duit la consommation de m??moire. Le calcul a ??t?? effectu?? sur un 64-noeud avec une superordinateur Hitachi t??raoctet de m??moire principale, capable d'effectuer 2000000000000 op??rations par seconde.

Un important d??veloppement r??cent a ??t?? la Formule BBP (formule BBP), d??couvert par Simon Plouffe et nomm?? d'apr??s les auteurs de l'article dans lequel la formule a d'abord ??t?? publi??, David H. Bailey, Peter Borwein et Plouffe. La formule,

est remarquable, car il permet l'extraction de toute personne hexad??cimal ou binaire chiffres de π sans calculer toutes les pr??c??dentes. Entre 1998 et 2000, le projet de calcul distribu?? PiHex utilis?? une modification de la formule en raison de BBP Fabrice Bellard pour calculer la quadrillioni??me (1,000,000,000,000,000: e) peu de π, qui se est av??r?? ??tre 0.

M??morisation des chiffres

R??cent d??cennies ont vu une augmentation du nombre record de chiffres m??moris??s.

M??me longtemps avant que les ordinateurs ont calcul?? π, la m??morisation d'un nombre record de chiffres est devenue une obsession pour certains. En 2006, Akira Haraguchi, un ing??nieur japonais ?? la retraite, a affirm?? avoir r??cit?? 100 000 d??cimales. Ceci, cependant, doit encore ??tre v??rifi?? par le Guinness World Records. Le record Guinness reconnu pour les chiffres rappel??s de π est 67890 chiffres, d??tenues par Lu Chao, un ??tudiant dipl??m?? de 24 ans en provenance de Chine. Il lui a fallu 24 heures et 4 minutes ?? r??citer ?? la d??cimale 67890e de π sans erreur.

Il existe de nombreux moyens pour m??moriser π, y compris l'utilisation de "piems", qui sont des po??mes qui repr??sentent π de telle sorte que la longueur de chaque mot (en lettres) repr??sente un chiffre. Voici un exemple d'une piem: Comment je ai besoin d'un verre, alcoolique dans la nature (ou: bien s??r)., Apr??s les conf??rences lourds impliquant la m??canique quantique Remarquez comment le premier mot a trois lettres, le deuxi??me mot a une, le troisi??me a 4, le quatri??me a une, la cinqui??me a 5, et ainsi de suite. Le Cadaeic Cadenza contient les 3834 premiers chiffres de π de cette mani??re. Piems sont li??s ?? l'ensemble du champ de l'??tude d'humour mais s??rieuse qui implique l'utilisation de techniques mn??motechniques pour se souvenir des chiffres de π, connus sous le nom Piphilology. Voir mn??moniques de Pi pour des exemples. Dans d'autres langues il existe des m??thodes similaires de m??morisation. Cependant, cette m??thode se av??re inefficace pour un grand m??morisations de pi. D'autres m??thodes incluent mod??les retenir sur les chiffres; par exemple, l'ann??e 1971 appara??t dans les cinquante premiers chiffres de pi.

Propri??t??s avanc??es

Approximations num??riques

En raison de la nature transcendantale de π, il n'y a pas de formulaire expressions ferm??s pour le nombre en termes de nombre et fonctions alg??briques. Les formules de calcul π en utilisant l'arithm??tique ??l??mentaire comprennent g??n??ralement s??rie ou notation de sommation (tels que "..."), ce qui indique que la formule est une formule pour vraiment une s??quence infinie d'approximations de π. Les plus termes inclus dans un calcul, la plus proche de π le r??sultat obtiendra.

Par cons??quent, les calculs num??riques doivent utiliser approximations de π. Pour de nombreuses raisons, ou 3,14 _^22/7 est assez proche, bien que les ing??nieurs utilisent souvent 3,1416 (5 chiffres significatifs) ou 3,14159 (six chiffres significatifs) pour plus de pr??cision. Les approximations _^22/7 et _^355/113, avec 3 et 7 chiffres significatifs respectivement, sont obtenues ?? partir de la simple d??veloppement en fraction continue de π. Le rapprochement _^355/113 (3,1415929 ...) est le meilleur qui peut ??tre exprim?? avec un ?? trois chiffres ou quatre chiffres num??rateur et le d??nominateur .

La premi??re approximation num??rique de π est presque certainement la valeur 3. Dans les cas o?? peu de pr??cision est n??cessaire, il peut ??tre un substitut acceptable. Ce 3 est une sous-estimation d??coule du fait que ce est le rapport de la un p??rim??tre de inscrit r??guli??re hexagonale au diam??tre du cercle .

Naturel

En g??om??trie non-euclidienne la somme des angles d'un triangle peut ??tre sup??rieure ou inf??rieure ?? π radians , et le rapport de la circonf??rence d'un cercle ?? son diam??tre peut ??galement ??tre diff??rent de π. Cela ne change pas la d??finition de π, mais il ne affecte de nombreuses formules dans lesquelles π appara??t. Ainsi, en particulier, π ne est pas affect??e par la forme de l'Univers; ce ne est pas un constante physique, mais une constante math??matique d??finie ind??pendamment de tout mesures physiques. N??anmoins, il se produit souvent en physique.

Par exemple, consid??rons la loi de Coulomb ( Unit??s SI):

Ici, quatre πr ² ne est que la surface de sph??re de rayon r. Dans cette forme, ce est un moyen pratique de d??crire la relation inverse du carr?? de la force ?? une distance r d'une source ponctuelle. Il serait bien s??r possible de d??crire cette loi dans d'autres, mais moins pratique fa??ons, ou dans certains cas plus pratique. Si Charge de Planck est utilis??, il peut ??tre ??crit comme

et ??liminer ainsi la n??cessit?? de π.

Questions ouvertes

La question ouverte la plus pressante ?? propos de π est de savoir si ce est un nombre normal - si un bloc de chiffres se produit dans l'expansion de π aussi souvent que l'on peut se attendre statistiquement si les chiffres avaient ??t?? produites enti??rement "au hasard", et que ce est vrai dans toutes les bases, pas baser juste 10. Les connaissances actuelles sur cette point est tr??s faible; par exemple, il ne est pas encore connu que des chiffres 0, ..., 9 se produisent souvent en continu dans le d??veloppement d??cimal de π.

Bailey et Crandall ont montr?? en 2000 que l'existence de l'mentionn??s ci-dessus Formule BBP et des formules similaires impliquent que la normalit?? en base 2 de π et de divers autres constantes peut ??tre r??duite ?? une plausible conjecture de la th??orie du chaos .

Il est ??galement inconnu si π et e sont alg??briquement ind??pendants, bien que Yuri Nesterenko a prouv?? l'ind??pendance alg??brique de {π, e ^π, Γ (1/4)} en 1996. Cependant, on sait que au moins un des πe et π + e est transcendantale (voir Th??or??me Lindemann-Weierstrass).

Utilisez en math??matiques et en sciences

π est omnipr??sent dans les math??matiques, apparaissant m??me dans les endroits qui ne ont pas un lien ??vident avec les cercles de la g??om??trie euclidienne.

G??om??trie et la trigonom??trie

Pour tout cercle de rayon r et de diam??tre d = 2 r, la circonf??rence est π D et la r??gion est π r ^2. En outre, π appara??t dans les formules pour les zones et les volumes de nombreuses autres formes g??om??triques bas??s sur des cercles, comme des ellipses , des sph??res , c??nes, et Tori . En cons??quence, π appara??t dans int??grales d??finies qui d??crivent circonf??rence, surface ou le volume des formes g??n??r??es par des cercles. Dans le cas de base, la moiti?? de la superficie de la Unit?? de disque est donn??e par:

et

donne la moiti?? de la circonf??rence de la cercle unit??. Des formes plus complexes peuvent ??tre int??gr??es en tant que solides de r??volution.

De la d??finition unit?? cercle des fonctions trigonom??triques suit ??galement que le sinus et cosinus ont p??riode 2π. Ce est, pour tout x et n entiers, sin (x) = sin (x + n 2π) et cos (x) = cos (x + n 2π). Parce que le p??ch?? (0) = 0, sin (2π n) = 0 pour tout entier n. En outre, la mesure d'angle de 180 ?? est ??gale ?? π radians. En d'autres termes, 1 ?? = (π / 180) radians.

En math??matiques modernes, π est souvent d??finie en utilisant les fonctions trigonom??triques, par exemple comme les plus petites x positifs pour lesquels sin x = 0, pour ??viter la d??pendance inutile sur les subtilit??s de la g??om??trie euclidienne et l'int??gration. ??quivalente, π peut ??tre d??finie en utilisant la fonctions trigonom??triques inverses, comme par exemple π 2 = arccos (0) = π 4 ou arctan (1). ??largir fonctions trigonom??triques inverses que s??rie de puissance est la meilleure fa??on de tirer s??rie infinie de π.

Analyse sup??rieur et de la th??orie des nombres

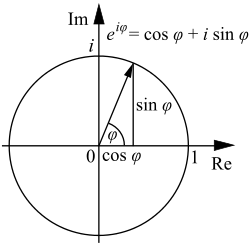
L'apparition fr??quente de π dans analyse complexe peut ??tre li??e au comportement de la fonction exponentielle d'une variable complexe, d??crit par La formule d'Euler

o?? i est l' unit?? imaginaire satisfaire i ² = -1 et e ≈ 2,71828 est Nombre d'Euler. Cette formule implique que les pouvoirs imaginaires d??crivent des rotations de l'e sur le cercle unit?? dans le plan complexe; ces rotations ont une p??riode de 360 ?? = 2π. En particulier, les 180 ?? = π φ r??sultats rotation dans le remarquable identit?? d'Euler

Il existe diff??rents n n -i??me racines de l'unit??

Le Int??grale de Gauss

Une cons??quence est que le fonction de gamma d'un demi-entier est un multiple rationnel de √π.

Physique

Le nombre π appara??t r??guli??rement dans les ??quations d??crivant des principes fondamentaux de l'Univers, dues en grande partie ?? sa relation avec la nature du cercle et, en cons??quence, les syst??mes de coordonn??es sph??rique.

• Le constante cosmologique:

• Le principe d'incertitude d'Heisenberg:

• L'??quation de champ d'Einstein de la relativit?? g??n??rale :

• La loi de Coulomb pour la force ??lectrique :

• La perm??abilit?? magn??tique d'espace libre:

• Troisi??me constante de la loi de Kepler :

Probabilit??s et statistiques

En probabilit?? et statistiques , il ya beaucoup de distributions dont les formules contiennent π, y compris:

• la fonction de densit?? de probabilit?? de la distribution normale de moyenne μ et d' ??cart type σ, en raison de la Int??grale gaussienne:

• la fonction de densit?? de probabilit?? pour la (standard) Distribution de Cauchy:

A noter que puisque 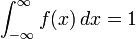pour une fonction de densit?? de probabilit?? f (x), les formules ci-dessus peuvent ??tre utilis??s pour produire d'autres formules int??grales pour π.

Le probl??me de l'aiguille de Buffon est parfois cit?? comme une approximation empirique de π dans ??math??matiques populaires" fonctionne. Envisager de laisser tomber une aiguille de longueur L ?? plusieurs reprises sur une surface contenant des lignes parall??les tir??s unit??s S en dehors (avec S> L). Si l'aiguille est tomb?? n fois et x de ces moments o?? il se immobilise en traversant une ligne (x> 0), alors on peut rapprocher π en utilisant la m??thode de Monte Carlo :

Bien que ce r??sultat est math??matiquement impeccable, il ne peut pas ??tre utilis??e pour d??terminer plus de tr??s peu de chiffres de π par l'exp??rience. Obtenir de fa??on fiable seulement trois chiffres (y compris l'initiale ??3??) exige le droit des millions de lancers, et le nombre de lancers cro??t de fa??on exponentielle avec le nombre de chiffres souhait??s. En outre, toute erreur dans la mesure de longueurs L et S transf??re directement ?? une erreur dans le π approch??e. Par exemple, une diff??rence d'un seul atome de la longueur d'une aiguille de 10 centim??tres appara??trait dans le neuvi??me chiffre du r??sultat. Dans la pratique, les incertitudes pour d??terminer si l'aiguille traverse effectivement une ligne quand il appara??t ?? toucher exactement il limitera la pr??cision atteignable ?? beaucoup moins de 9 chiffres.