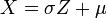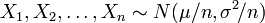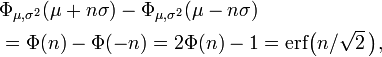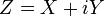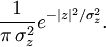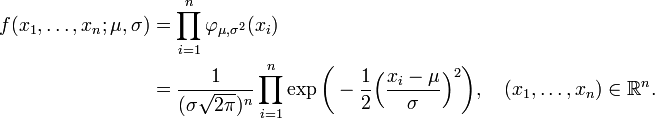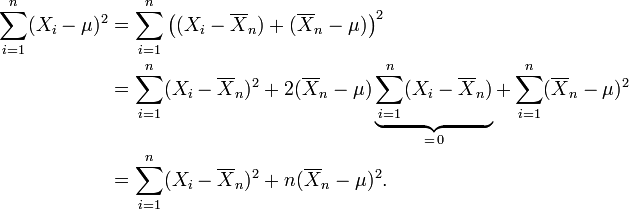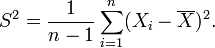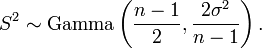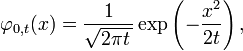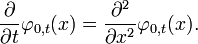Distribution normale
Contexte des ??coles Wikip??dia
Enfants SOS offrent un chargement complet de la s??lection pour les ??coles pour une utilisation sur les intranets des ??coles. Cliquez ici pour plus d'informations sur les enfants SOS.
Densit?? de probabilit??  La ligne verte est la distribution normale standard | |
Fonction de distribution cumulative  Couleurs correspondent ?? l'image ci-dessus | |
| Param??tres | 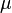 emplacement ( r??el ) emplacement ( r??el ) 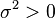 quadrill?? ??chelle (r??el) quadrill?? ??chelle (r??el) |
|---|---|
| Soutien | 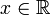 |
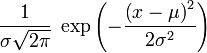 | |
| CDF | 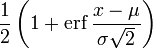 |
| Signifier | 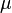 |
| M??diane | 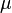 |
| Mode | 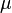 |
| Variance | 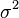 |
| Asym??trie | 0 |
| Ex. aplatissement | 0 |
| Entropy | 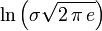 |
| MGF | 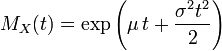 |
| FC |  |
La distribution normale, aussi appel??e la distribution gaussienne, est une importante famille de distributions de probabilit??s continues , applicable dans de nombreux domaines. Chaque membre de la famille peut ??tre d??finie par deux param??tres, l'emplacement et d'??chelle: la moyenne (??moyenne??, μ) et la variance ( ??cart-type carr??) σ 2, respectivement. La distribution normale est la distribution normale avec une moyenne de z??ro et un ??cart d'une (les courbes vertes dans les parcelles vers la droite). Carl Friedrich Gauss est devenu associ?? ?? cet ensemble de distributions quand il a analys?? les donn??es astronomiques de les utiliser, et d??fini l'??quation de la fonction de densit?? de probabilit??. On l'appelle souvent la courbe en cloche, car le diagramme de son densit?? de probabilit?? ressemble ?? un cloche.
L'importance de la distribution normale en tant que mod??le de ph??nom??nes quantitatives dans le naturel et sciences du comportement est d?? ?? la th??or??me central limite. Beaucoup psychologiques et mesures physiques (ph??nom??nes comme bruit) peut ??tre bien approch??e par la distribution normale. Bien que les m??canismes qui sous-tendent ces ph??nom??nes sont souvent inconnus, l'utilisation du mod??le normal peut ??tre justifi?? en supposant que th??oriquement, de nombreux petits effets ind??pendants sont additivement contribuent ?? chaque observation.
La distribution normale se pose ??galement dans de nombreux domaines de statistiques . Par exemple, le distribution d'??chantillonnage de la moyenne ??chantillon est approximativement normale, m??me si la distribution de la population ?? partir de laquelle l'??chantillon est pr??lev?? ne est pas normal. En outre, la distribution normale maximise entropie de l'information entre toutes les distributions ?? moyenne et la variance connue, ce qui rend le choix naturel de distribution sous-jacente des donn??es r??sum??es en termes de moyenne de l'??chantillon et la variance. La distribution normale est la famille la plus largement utilis??e dans les statistiques des distributions et de nombreux tests statistiques sont fond??es sur l'hypoth??se de normalit??. Dans la th??orie des probabilit??s , distributions normales apparaissent comme limiter les distributions de plusieurs continues et discr??tes familles de distributions.
Histoire
La distribution normale a ??t?? introduite par Abraham de Moivre dans un article en 1733, qui a ??t?? reproduit dans la deuxi??me ??dition de son La th??orie des probabilit??s, 1738 dans le contexte de rapprochement de certaines distributions binomiale pour n grand. Son r??sultat a ??t?? prolong??e par Laplace dans son livre Th??orie analytique des probabilit??s (1812), et se appelle d??sormais la th??or??me de Moivre-Laplace.
Laplace utilise la distribution normale dans le analyse des erreurs d'exp??riences. L'importance m??thode des moindres carr??s a ??t?? introduit par Legendre en 1805. Gauss , qui pr??tendait avoir utilis?? la m??thode depuis 1794, a justifi?? rigoureusement en 1809 en supposant une distribution normale des erreurs.
Le nom de ??courbe en cloche?? remonte ?? Jouffret qui d'abord utilis?? le terme ??surface de cloche?? en 1872 pour une bivari??e normale avec des composants ind??pendants. Le nom de ??distribution normale?? a ??t?? invent?? ind??pendamment par Charles S. Peirce, Francis Galton et Wilhelm Lexis vers 1875. Malgr?? cette terminologie, d'autres distributions de probabilit?? peut ??tre plus appropri?? dans certains contextes; voir la discussion de survenance , ci-dessous.
Caract??risation
Il existe diverses fa??ons ?? caract??riser une distribution de probabilit?? . Le visuel est la plus fonction de densit?? de probabilit?? (PDF). Mani??res ??quivalentes sont les fonction de distribution cumulative, la moments, le cumulants, le fonction caract??ristique, le Fonction g??n??ratrice des moments, le cumulant- fonction g??n??ratrice, et Le th??or??me de Maxwell. Voir distribution de probabilit?? pour une discussion.
Pour indiquer qu'une valeur r??elle variable al??atoire X est normalement distribu?? avec une moyenne μ et de variance σ ?? ≥ 0, nous ??crivons
M??me se il est certainement utile pour certains th??or??mes limites (par exemple, normalit?? asymptotique des estimateurs) et de la th??orie de la Processus gaussiens ?? consid??rer la distribution de probabilit?? concentr??e ?? μ (voir Mesure de Dirac) comme une distribution normale de moyenne μ et de variance σ ?? = 0, ce cas d??g??n??r?? est souvent exclue des consid??rations parce que personne ne la densit?? par rapport ?? la Mesure de Lebesgue existe.
La distribution normale peut ??galement ??tre param??tr?? en utilisant un pr??cision param??tre τ, d??finie comme l'inverse de σ ??. Ce param??trage a un avantage dans les applications num??riques o?? σ ?? est tr??s proche de z??ro et est plus commode de travailler avec l'analyse que τ est un param??tre physique de la distribution normale.
Densit?? de probabilit??

Le continu fonction de densit?? de probabilit?? de la distribution normale est le Gaussienne
o?? σ> 0 est l' ??cart-type , le param??tre μ r??el est le valeur attendue, et
est la fonction de densit?? de la distribution normale "standard", ce est ?? dire, la distribution normale avec μ = 0 et σ = 1. Le int??grante de 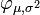 au dessus de ligne r??elle est ??gale ?? un, comme indiqu?? dans la Article int??grante gaussienne.
au dessus de ligne r??elle est ??gale ?? un, comme indiqu?? dans la Article int??grante gaussienne.
Comme une fonction gaussienne avec le d??nominateur de l'exposant ??gale ?? 2, la fonction de densit?? normale standard  est un fonction propre de la Transform??e de Fourier.
est un fonction propre de la Transform??e de Fourier.
La fonction de densit?? de probabilit?? pr??sente des propri??t??s remarquables, notamment:
- sym??trie par rapport ?? ses moyens μ
- la Mode et de la m??diane ?? la fois ??gale ?? la moyenne μ
- la points de la courbe d'inflexion se produisent un ??cart-type loin de la moyenne, ce est ?? dire au μ - σ et μ + σ.
Fonction de distribution cumulative

Le fonction de distribution cumulative (CDF de) d'une distribution de probabilit?? , ??valu??e ?? un certain nombre (minuscules) x, est la probabilit?? de l'??v??nement ayant une variable al??atoire (capital) X avec cette r??partition est inf??rieur ou ??gal ?? x. La fonction de distribution cumulative de la distribution normale est exprim??e en termes de la fonction de densit?? de la mani??re suivante:
o?? la fonction de r??partition normale standard, Φ, est juste la cdf g??n??rale ??valu??e avec μ = 0 et σ = 1:
Le cdf normale standard peut ??tre exprim??e en termes de fonction sp??ciale appel??e fonction d'erreur, en tant que
et la fonction de r??partition lui-m??me peut donc ??tre exprim??e comme
Le compl??ment de la fonction de r??partition normale standard, 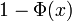 , Est souvent d??sign??
, Est souvent d??sign?? 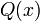 , Et est parfois d??sign?? simplement comme la Q-fonction, en particulier dans les textes d'ing??nierie. Cela repr??sente la probabilit?? queue de la distribution gaussienne. D'autres d??finitions de la fonction de Q, qui sont toutes des transformations simples
, Et est parfois d??sign?? simplement comme la Q-fonction, en particulier dans les textes d'ing??nierie. Cela repr??sente la probabilit?? queue de la distribution gaussienne. D'autres d??finitions de la fonction de Q, qui sont toutes des transformations simples 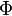 , Sont ??galement utilis??s parfois.
, Sont ??galement utilis??s parfois.
L'inverse fonction standard de distribution cumulative normale, ou fonction quantile, peut ??tre exprim??e en termes de la fonction d'erreur inverse:
et la fonction cumulative inverse de distribution peut donc ??tre exprim??e comme
Cette fonction quantile est parfois appel?? le fonction probit. Il n'y a pas ??l??mentaire primitive de la fonction de probit. Ce ne est pas de dire simplement que rien ne est connu, mais plut??t que la non-existence d'une telle primitive ??l??mentaire a ??t?? prouv??. Plusieurs m??thodes pr??cises existent pour l'approximation de la fonction quantile pour la distribution normale - voir fonction quantile pour une discussion et r??f??rences.
Les valeurs Φ (x) peuvent ??tre estim??s de fa??on tr??s pr??cise par une vari??t?? de m??thodes, telles que l'int??gration num??rique , la s??rie de Taylor , s??rie asymptotique et fractions continues.
Limites strictes inf??rieures et sup??rieures pour la cdf
Pour les grandes x la cdf normale standard 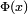 est proche de 1 et
est proche de 1 et 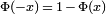 est proche de 0. Les limites ??l??mentaires
est proche de 0. Les limites ??l??mentaires
en termes de la densit??  sont utiles.
sont utiles.
En utilisant le substitution v = u ?? / 2, la limite sup??rieure est calcul??e comme suit:
De m??me, en utilisant  et le r??gle de quotient,
et le r??gle de quotient,
La r??solution de  fournit la borne inf??rieure.
fournit la borne inf??rieure.
Fonctions g??n??ratrices
Moment fonction de production
Le fonction g??n??ratrice des moments est d??finie comme la valeur attendue de exp (TX). Pour une distribution normale, la fonction g??n??ratrice des moments est
comme on peut le voir par compl??tant le carr?? de l'exposant.
Fonction g??n??ratrice des cumulants
Le cumulant fonction g??n??ratrice est le logarithme de la fonction g??n??ratrice des moments: g (t) = μ t + s?? t ?? / 2. Puisque ce est un polyn??me quadratique en t, seuls les deux premiers cumulants sont non nulles.
Fonction caract??ristique
Le fonction caract??ristique est d??finie comme la valeur attendue de 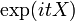 O??
O?? 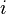 est l' unit?? imaginaire . Ainsi, la fonction caract??ristique est obtenue en rempla??ant
est l' unit?? imaginaire . Ainsi, la fonction caract??ristique est obtenue en rempla??ant 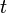 avec
avec  dans la fonction g??n??ratrice des moments.
dans la fonction g??n??ratrice des moments.
Pour une distribution normale, la fonction caract??ristique est
Propri??t??s
Certaines propri??t??s de la distribution normale:
- Si
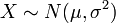 et
et  et
et 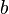 sont des nombres r??els , puis
sont des nombres r??els , puis 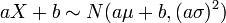 (Voir valeur attendue et la variance ).
(Voir valeur attendue et la variance ). - Si
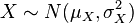 et
et  sont normales ind??pendantes variables al??atoires , puis:
sont normales ind??pendantes variables al??atoires , puis: - Leur somme est normalement distribu?? avec
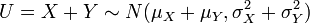 ( la preuve). Fait int??ressant, l'inverse est vrai: si deux variables al??atoires ind??pendantes ont une somme normalement distribu??, alors ils doivent ??tre normales eux-m??mes - ce est connu comme Le th??or??me de Cramer.
( la preuve). Fait int??ressant, l'inverse est vrai: si deux variables al??atoires ind??pendantes ont une somme normalement distribu??, alors ils doivent ??tre normales eux-m??mes - ce est connu comme Le th??or??me de Cramer. - Leur diff??rence est normalement distribu?? avec
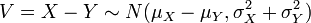 .
. - Si les variances de X et Y sont ??gaux, alors U et V sont ind??pendantes les unes des autres.
- Le Kullback-Leibler,
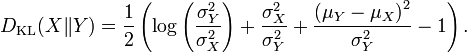
- Leur somme est normalement distribu?? avec
- Si
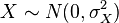 et
et 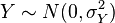 sont des variables al??atoires normales ind??pendantes, alors:
sont des variables al??atoires normales ind??pendantes, alors: - Leur produit
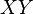 suit une distribution de densit??
suit une distribution de densit?? 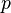 donn?? par
donn?? par 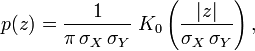 o??
o?? 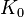 est une fonction de Bessel modifi??e de deuxi??me esp??ce .
est une fonction de Bessel modifi??e de deuxi??me esp??ce .
- Leur rapport suit une Distribution de Cauchy avec
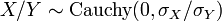 . Ainsi, la distribution de Cauchy est un type sp??cial de R??partition de rapport.
. Ainsi, la distribution de Cauchy est un type sp??cial de R??partition de rapport.
- Leur produit
- Si
 sont des variables normales standard ind??pendantes, puis
sont des variables normales standard ind??pendantes, puis 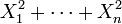 a une distribution chi-carr?? avec n degr??s de libert??.
a une distribution chi-carr?? avec n degr??s de libert??.
La normalisation des variables al??atoires normales
Du fait de la propri??t?? 1, il est possible de relier ensemble des variables al??atoires normales ?? la normale standard.
Si 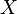 ~
~ 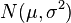 , Puis
, Puis
est une variable al??atoire normale standard: 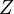 ~
~ 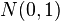 . Une cons??quence importante est que la fonction de r??partition d'une distribution normale g??n??rale est donc
. Une cons??quence importante est que la fonction de r??partition d'une distribution normale g??n??rale est donc
Inversement, si 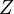 est une distribution normale standard,
est une distribution normale standard, 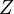 ~
~ 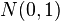 , Puis
, Puis
est une variable al??atoire normale de moyenne 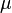 et la variance
et la variance 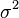 .
.
La distribution normale standard a ??t?? totalis??es (g??n??ralement sous la forme de la valeur de la distribution cumulative fonction Φ), et les autres distributions normales sont les transformations simples, comme d??crit ci-dessus, d'une norme. Par cons??quent, on peut utiliser les valeurs des tables de la fonction de r??partition de la distribution normale standard pour trouver les valeurs de la fonction de r??partition d'une distribution normale g??n??ral.
Moments
Les premi??res des moments de la distribution normale sont:
| Nombre | Raw instant | Moment central | Cumulant |
|---|---|---|---|
| 0 | 1 | 1 | |
| 1 | 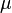 | 0 | 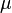 |
| 2 | 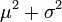 | 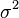 | 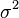 |
| 3 | 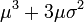 | 0 | 0 |
| 4 | 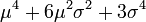 | 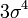 | 0 |
| 5 | 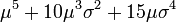 | 0 | 0 |
| 6 | 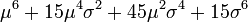 |  | 0 |
| 7 | 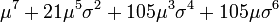 | 0 | 0 |
| 8 | 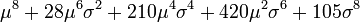 | 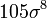 | 0 |
Tous cumulants de la distribution normale-del?? de la seconde sont nuls.
Moments centraux plus ??lev??s (de l'ordre  avec
avec 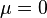 ) Peut ??tre obtenu en utilisant la formule
) Peut ??tre obtenu en utilisant la formule
![E \ left [x ^ {2k} \ right] = \ frac {(2k)!} {2 ^ kk!} \ Sigma ^ {} 2k.](../../images/109/10941.png)
G??n??rer des valeurs pour les variables al??atoires normales
Pour les simulations sur ordinateur, il est souvent utile pour g??n??rer des valeurs qui ont une distribution normale. Il existe plusieurs m??thodes et le plus fondamental est d'inverser la fonction de r??partition normale standard. Des m??thodes plus efficaces sont ??galement connus, une telle m??thode ??tant la Box-Muller transformer. Un algorithme encore plus rapide est le algorithme de ziggourat.
L'algorithme de Box-Muller dit que, si vous avez deux nombres a et b r??parties uniform??ment sur (0, 1], (par exemple la sortie d'un g??n??rateur de nombres al??atoires), puis deux variables al??atoires standards normalement distribu??s sont c et d, o??:
Ce est parce que la distribution du chi carr?? avec deux degr??s de libert?? (voir la propri??t?? 4 ci-dessus) est une variable al??atoire exponentielle facilement g??n??r??.
Le th??or??me central limite
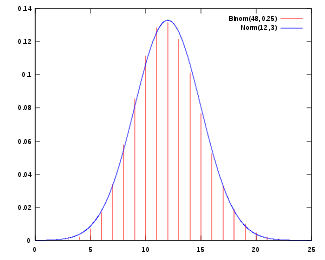
Dans certaines conditions (comme ??tre ind??pendants et identiquement distribu??s de variance finie), la somme d'un grand nombre de variables al??atoires est normalement distribu?? environ - ce est le th??or??me central limite.
L'importance pratique du th??or??me de la limite centrale est que la fonction de distribution normale cumulative peut ??tre utilis??e comme une approximation pour d'autres fonctions de distribution cumulative, par exemple:
- Une loi binomiale de param??tres n et p est approximativement normale pour les grands n et p pas trop pr??s de 1 ou 0 (certains livres vous recommandons d'utiliser cette approximation que si np et n (1 - p) sont ?? la fois au moins 5; dans ce cas, une correction de continuit?? doit ??tre appliqu??).
La distribution normale approximation a des param??tres μ = np, σ 2 = np (1 - p).
- Une distribution de Poisson de param??tre λ est ?? peu pr??s normale pour les grands λ.
La distribution normale d'approximation des param??tres μ a = σ 2 = λ.
Que ces approximations sont suffisamment pr??cise d??pend de l'usage auquel ils sont n??cessaires, et le taux de convergence de la distribution normale. Ce est g??n??ralement le cas que ces approximations sont moins pr??cises dans les queues de la distribution. Un sup??rieur g??n??ral li?? de l'erreur d'approximation de la fonction de distribution cumulative est donn??e par la Th??or??me de Berry-Ess??en.
Infinie divisibilit??
Les distributions normales sont infiniment divisibles distributions de probabilit??: ??tant donn?? une moyenne μ, une variance σ 2 ≥ 0, et un nombre naturel n, la somme X + 1. . . + X n de n variables al??atoires ind??pendantes
a cette distribution normale sp??cifi??e (pour v??rifier cela, l'utilisation ou fonctions caract??ristiques convolution et induction math??matique).
Stabilit??
Les distributions normales sont strictement distributions de probabilit?? stables.
Intervalles de rectification et de confiance standard

Environ 68% des valeurs tir??es d'une distribution normale sont ?? moins d'un ??cart-type σ de> 0 loin de la moyenne μ; environ 95% des valeurs sont ?? deux ??carts-types et environ 99,7% se situent dans trois ??carts-types. Ceci est connu comme le " R??gle 68-95-99.7 "ou la" r??gle empirique. "
Pour ??tre plus pr??cis, l'aire sous la courbe en cloche entre μ - n σ et μ + n σ en termes de la fonction de distribution normale cumulative est donn??e par
o?? erf est la fonction d'erreur. Pour 12 d??cimales, les valeurs de la 1-, 2-, jusqu'?? des points 6-sigma sont:
 | 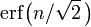 |
|---|---|
| 1 | ,682689492137 |
| 2 | ,954499736104 |
| 3 | ,997300203937 |
| 4 | ,999936657516 |
| 5 | ,999999426697 |
| 6 | ,999999998027 |
Le tableau suivant donne la relation inverse de multiples sigma correspondant ?? quelques valeurs souvent utilis??es pour l'aire sous la courbe en cloche. Ces valeurs sont utiles pour d??terminer (asymptotique) intervalles de confiance des niveaux sp??cifi??s pour normalement distribu??s (ou asymptotiquement normal) estimateurs:
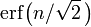 |  |
|---|---|
| 0,80 | 1,28155 |
| 0,90 | 1,64485 |
| 0,95 | 1,95996 |
| 0,98 | 2,32635 |
| 0,99 | 2,57583 |
| 0,995 | 2,80703 |
| 0,998 | 3,09023 |
| 0,999 | 3,29052 |
o?? la valeur du c??t?? gauche de la table est la proportion de valeurs qui tombent dans un intervalle donn??, et n est un multiple de l'??cart-type d??finissant la largeur de l'intervalle.
Formulaire de famille exponentielle
La distribution normale est une ?? deux param??tres formulaire de famille exponentielle naturelle avec des param??tres μ et 1 / σ 2, et des statistiques naturelles X et X 2. La forme canonique a param??tres  et
et 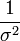 et statistiques suffisantes,
et statistiques suffisantes,  et
et 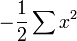 .
.
Processus gaussien complexe
Consid??rez variable al??atoire gaussienne complexe,
o?? X et Y sont des variables r??elles et ind??pendantes gaussiennes ayant des variances ??gales 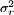 . Le pdf des variables communes est alors
. Le pdf des variables communes est alors
Parce que 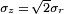 , Le PDF r??sultant pour le complexe gaussien variables Z est
, Le PDF r??sultant pour le complexe gaussien variables Z est
Distributions connexes
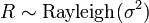 est un Distribution de Rayleigh si
est un Distribution de Rayleigh si 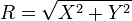 o??
o??  et
et 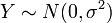 sont deux distributions normales ind??pendantes.
sont deux distributions normales ind??pendantes. 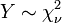 est une distribution chi-carr?? avec
est une distribution chi-carr?? avec 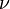 degr??s de libert?? si
degr??s de libert?? si 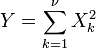 o??
o?? 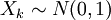 pour
pour 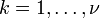 et sont ind??pendants.
et sont ind??pendants. 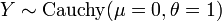 est un Distribution de Cauchy si
est un Distribution de Cauchy si 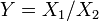 pour
pour  et
et 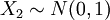 sont deux distributions normales ind??pendantes.
sont deux distributions normales ind??pendantes. 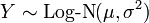 est un la distribution log-normale si
est un la distribution log-normale si 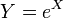 et
et 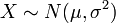 .
. - Rapport ?? La distribution alpha-stable biais L??vy: si
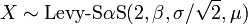 puis
puis 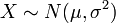 .
.
- Distribution normale tronqu??e. Si
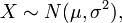 puis tronquer X ci-dessous au
puis tronquer X ci-dessous au 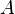 et au-dessus
et au-dessus 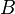 conduira ?? une variable al??atoire de moyenne
conduira ?? une variable al??atoire de moyenne 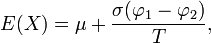 o??
o?? 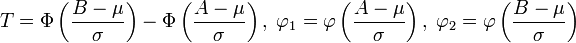 et
et  est le fonction de densit?? de probabilit?? d'une variable al??atoire normale standard.
est le fonction de densit?? de probabilit?? d'une variable al??atoire normale standard.
- Si
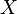 est une variable al??atoire avec une distribution normale, et
est une variable al??atoire avec une distribution normale, et  , Puis
, Puis  a un pli??e distribution normale.
a un pli??e distribution normale.
Les statistiques descriptives et inf??rentielles
Partitions
Beaucoup de points sont d??riv??es de la distribution normale, y compris rangs centiles (??percentiles??), Les ??quivalents de courbe normale, stanines, z-scores, et T-score. En outre, un certain nombre de comportements statistiques proc??dures sont fond??es sur l'hypoth??se que les scores sont normalement distribu??s; par exemple, des t-tests et Des analyses de variance (voir ci-dessous). Bell a courbe classement attribue notes relatives bas??es sur une distribution normale des scores.
Tests de normalit??
Tests de normalit?? v??rifier un ensemble donn?? de donn??es pour similitude avec la distribution normale. Le hypoth??se nulle est que l'ensemble de donn??es est similaire ?? la distribution normale, donc suffisamment faible P-valeur indique que les donn??es non-normales.
- Test de Kolmogorov-Smirnov
- Test de Lilliefors
- Test d'Anderson-Darling
- Test Ryan-Joiner
- Test de Shapiro-Wilk
- Trac?? de probabilit?? normale ( Rankit parcelle)
- Test de Jarque-Bera
Estimation des param??tres
Maximum de vraisemblance des param??tres
Supposer
sont ind??pendante et chacun est normalement distribu?? avec esp??rance μ et de variance σ ??> 0. Dans le langage des statisticiens, les valeurs observ??es de ces variables al??atoires n forment un "??chantillon de taille n ?? partir d'une population distribu??e normalement." Il est souhaitable d'estimer la ??population signifie" μ et la ????cart type de population??, σ, bas??es sur les valeurs observ??es de cet ??chantillon. La fonction de densit?? de probabilit?? conjointe continue de ces variables al??atoires ind??pendantes est n
En fonction de μ et σ, la fonction de vraisemblance sur la base des observations X 1, ..., X n est
avec une constante C> 0 (qui, en g??n??ral serait m??me permis de d??pendre de X 1, ..., X n, mais dispara??tront de toute fa??on quand d??riv??es partielles de la fonction de log-vraisemblance par rapport aux param??tres sont calcul??s, voir ci-dessous ).
Dans le proc??d?? de maximum de vraisemblance, les valeurs de μ et σ qui maximisent la fonction de vraisemblance sont pris comme des estimations de la population param??tres μ et σ.
Habituellement ?? maximiser une fonction de deux variables, on pourrait envisager d??riv??es partielles. Mais ici, nous allons exploiter le fait que la valeur de μ qui maximise la fonction de vraisemblance avec σ fixe ne d??pend pas de σ. Par cons??quent, nous pouvons constater que la valeur de μ, puis substituer ?? μ dans la fonction de vraisemblance, et enfin trouver la valeur de σ qui maximise l'expression r??sultante.
Il est ??vident que la fonction de vraisemblance est une fonction d??croissante de la somme
Donc, nous voulons la valeur de μ qui minimise cette somme. Laisser
??tre la "moyenne de l'??chantillon" sur la base des observations n. Observez que
Seul le dernier terme d??pend de μ et il est minimis?? par
Ce est l'estimation du maximum de vraisemblance de μ en fonction des n observations X 1, ..., X n. Lorsque nous substituons cette estimation pour μ dans la fonction de vraisemblance, nous obtenons
Il est classique pour d??signer la fonction "log-likelihood", ce est ?? dire le logarithme de la fonction de vraisemblance, par un minuscule  , Et nous avons
, Et nous avons
et puis
Ce d??riv?? est positive, nulle ou n??gative selon que σ ?? est entre 0 et
ou ??gale ?? cette quantit??, ou sup??rieure ?? cette quantit??. (Si il ya juste une observation, ce qui signifie que n = 1, ou si X = 1 ... n = X, qui ne arrive avec une probabilit?? z??ro, 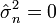 par cette formule, ce qui refl??te le fait que, dans ces cas, la fonction de vraisemblance ne est pas born?? comme σ diminue ?? z??ro.)
par cette formule, ce qui refl??te le fait que, dans ces cas, la fonction de vraisemblance ne est pas born?? comme σ diminue ?? z??ro.)
En cons??quence de cette moyenne des carr??s des r??sidus est l'estimation du maximum de vraisemblance de σ ??, et sa racine carr??e est l'estimation du maximum de vraisemblance de σ sur la base des n observations. Cet estimateur  est sollicit??, mais a un plus petit l'erreur quadratique moyenne de l'estimateur sans biais d'habitude, qui est n / (n - 1) fois cet estimateur.
est sollicit??, mais a un plus petit l'erreur quadratique moyenne de l'estimateur sans biais d'habitude, qui est n / (n - 1) fois cet estimateur.
G??n??ralisation Surprenant
Le calcul de l'estimateur du maximum de vraisemblance de la matrice de covariance d'un distribution normale multivari??e est subtile. Il se agit de la th??or??me spectral et la raison, il peut ??tre pr??f??rable de voir un scalaire comme le trace d'un 1 ?? 1 matrice que comme un simple scalaire. Voir estimation des matrices de covariance.
Impartiale estimation des param??tres
L'estimateur du maximum de vraisemblance de la moyenne de population 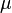 ?? partir d'un ??chantillon est un estimateur non biais?? de la moyenne, comme ce est la variance lorsque la moyenne de la population est connu a priori. Cependant, si nous sommes confront??s ?? un ??chantillon et ne ont aucune connaissance de la moyenne ou la variance de la population dont il est tir??, l'estimateur sans biais de la variance
?? partir d'un ??chantillon est un estimateur non biais?? de la moyenne, comme ce est la variance lorsque la moyenne de la population est connu a priori. Cependant, si nous sommes confront??s ?? un ??chantillon et ne ont aucune connaissance de la moyenne ou la variance de la population dont il est tir??, l'estimateur sans biais de la variance 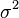 est:
est:
Cette ??variance de l'??chantillon" suit une Distribution Gamma si tous les X i sont ind??pendants et identiquement distribu??s:
Occurrence
Environ distributions normales se produisent dans de nombreuses situations, en raison de la th??or??me central limite. Lorsqu'il existe des raisons de soup??onner la pr??sence d'un grand nombre de petits effets qui agissent de fa??on additive et ind??pendamment, il est raisonnable de supposer que les observations seront normaux. Il existe des m??thodes statistiques pour tester empiriquement cette hypoth??se, par exemple, le Test de Kolmogorov-Smirnov.
Les effets peuvent aussi agir comme multiplicateurs modifications (plut??t que additifs). Dans ce cas, l'hypoth??se de normalit?? ne est pas justifi??e, et ce est le logarithme de la variable d'int??r??t qui est normalement distribu??. La distribution de la variable directement observ?? est alors appel?? log-normale.
Enfin, se il ya une seule influence ext??rieure qui a un grand effet sur la variable ?? l'??tude, l'hypoth??se de normalit?? ne est pas justifi?? non plus. Ce est vrai m??me si, lorsque la variable externe est maintenue constante, les distributions marginales r??sultant sont en effet normal. La distribution compl??te sera une superposition de variables normales, qui ne est pas en g??n??ral normale. Ceci est li?? ?? la th??orie des erreurs (voir ci-dessous).
Pour r??sumer, voici une liste des situations o?? la normalit?? approximative suppose parfois. Pour une discussion plus approfondie, voir ci-dessous.
- Dans les probl??mes de comptage (de sorte que le th??or??me central limite comprend une approximation discr??te ?? continuum) o?? variables al??atoires de reproduction sont impliqu??s, tels que
- Variables al??atoires binomiales , associ??s aux questions oui / non;
- Variables al??atoires de Poisson , associ??e ?? des ??v??nements rares;
- Dans les mesures physiologiques de sp??cimens biologiques:
- Le logarithme de mesures de la taille des tissus vivants (longueur, hauteur, surface de la peau, poids);
- La longueur des appendices inertes (cheveux, les ongles, les griffes, dents) des ??chantillons biologiques, dans la direction de la croissance; sans doute l'??paisseur de l'??corce d'arbre tombe ??galement dans cette cat??gorie;
- Autres mesures physiologiques peuvent ??tre distribu??es normalement, mais il n'y a aucune raison de se attendre ?? ce que, a priori;
- Les erreurs de mesure sont souvent suppos??es ??tre distribu??es normalement, et tout ??cart par rapport ?? la normalit?? est consid??r?? comme quelque chose qui doit ??tre expliqu??;
- Les variables financi??res
- Les changements dans le logarithme des taux de change, les indices des prix, et les indices boursiers; ces variables se comportent comme l'int??r??t compos??, pas comme un int??r??t simple, et sont donc multiplicatif;
- Autres variables financi??res peuvent ??tre distribu??es normalement, mais il n'y a aucune raison de se attendre ?? ce que, a priori;
- L'intensit?? lumineuse
- L'intensit?? de la lumi??re laser est normalement distribu??;
- La lumi??re thermique a une La distribution de Bose-Einstein sur des ??chelles de temps tr??s courts, et une distribution normale sur des ??ch??ances plus longues en raison de la th??or??me central limite.
De l'int??r??t pour la biologie et de l'??conomie est le fait que les syst??mes complexes ont tendance ?? afficher lois de puissance plut??t que la normalit??.
Comptage de photons
L'intensit?? lumineuse d'une source unique varie avec le temps, que les fluctuations thermiques peuvent ??tre observ??es si la lumi??re est analys??e avec une r??solution de temps suffisamment ??lev??. L'intensit?? est g??n??ralement suppos?? ??tre normalement distribu??s. La m??canique quantique interpr??te mesures de l'intensit?? de lumi??re photon comptage. L'hypoth??se naturelle dans ce cadre est la distribution de Poisson . Lorsque l'intensit?? lumineuse est int??gr??e sur fois plus longtemps que le temps de coh??rence et est grand, la limite de Poisson-??-normale est appropri??.
Les erreurs de mesure
La normalit?? est l'hypoth??se centrale de la math??matique th??orie des erreurs. De m??me, dans le mod??le statistique raccord, un indicateur de qualit?? de l'ajustement est que le r??sidus (comme les erreurs sont appel??s dans ce cadre) soient ind??pendants et distribu??s normalement. L'hypoth??se est que tout ??cart par rapport ?? la normalit?? doit ??tre expliqu??. En ce sens, ?? la fois dans le mod??le ajust?? et dans la th??orie des erreurs, la normalit?? est la seule observation qui ne doivent pas ??tre expliqu??, ??tant pr??vu. Toutefois, si les donn??es d'origine ne sont pas normalement distribu??es (par exemple se ils suivent une Cauchy distribution), les r??sidus ne seront pas ??galement distribu??es normalement. Ce fait est g??n??ralement ignor?? dans la pratique.
Des mesures r??p??t??es de la m??me quantit?? devraient donner des r??sultats qui sont regroup??s autour d'une valeur particuli??re. Si toutes les sources principales d'erreurs ont été prises en compte, il est supposé que l'erreur restante doit être le résultat d'un grand nombre de très petites additifs effets, et donc normal. Les écarts à la normalité sont interprétées comme des indications d'erreurs systématiques qui ne sont pas prises en compte. Si cette hypothèse est valable est discutable. Une remarque célèbre et souvent citée attribué à Gabriel Lippmann dit: «Tout le monde croit en la loi [normale] d'erreurs: les mathématiciens, parce qu'ils pensent qu'il est un fait expérimental, et les expérimentateurs, parce qu'ils supposent qu'il est un théorème de mathématiques ».
Les caractéristiques physiques des échantillons biologiques
Les tailles des animaux adultes est d'environ log-normale. La preuve et une explication basée sur les modèles de croissance a été publié la première fois en 1932 le livre problèmes de croissance relative par Julian Huxley.
Les différences de taille en raison de dimorphisme sexuel, ou d'autres polymorphismes comme le travailleur / soldat / division reine chez les insectes sociaux, font en outre la distribution des tailles dévier de lognormalité.
L'hypothèse selon laquelle la taille linéaire d'échantillons biologiques est normal (plutôt que log-normale) conduit à une distribution non normale des poids (puisque le poids ou le volume est à peu près proportionnelle à la 2ème ou 3ème puissance de longueur, et les distributions gaussiennes ne sont conservés par des transformations linéaires ), et inversement en supposant que le poids est conduit normales à des longueurs non-normales. Ceci est un problème, car il n'y a pas a priori de raison pour laquelle on la longueur ou la masse corporelle, et pas l'autre, devrait être distribué normalement. Distributions lognormales, d'autre part, sont conservés par les puissances de sorte que le «problème» disparaît si lognormalité est supposé.
D'autre part, il ya quelques mesures biologiques où la normalité est supposé, comme la pression artérielle d'êtres humains adultes. Cela est censé être normalement distribué, mais seulement après avoir séparé les mâles et les femelles dans différentes populations (dont chacun est normalement distribué).
Les variables financi??res
D??j?? en 1900 Louis Bachelier propos?? repr??sentant des variations de prix des actions ?? l'aide de la distribution normale. Cette approche a depuis été légèrement modifié. En raison de la nature exponentielle de l'inflation , les indicateurs financiers tels que les actions et les valeurs des matières premières les prix présentent "un comportement multiplicatif". En tant que tel, leurs changements périodiques (par exemple, les changements annuels) ne sont pas normaux, mais plutôt lognormale - c.-à- retours par opposition aux valeurs sont normalement distribués. Ceci est encore l'hypothèse la plus couramment utilisée dans la finance , en particulier dans l'évaluation des actifs. Corrections apportées à ce modèle semblent être nécessaires, comme cela a été souligné par exemple par Benoît Mandelbrot, le vulgarisateur de fractales , qui a observé que les changements dans logarithme sur de courtes périodes (comme un jour) sont bien approchées par des distributions qui ne disposent pas variance finie, et donc le théorème central limite ne sont pas applicables. Plutôt, la somme de beaucoup de ces changements donne distributions log-Levy.
Répartition dans les tests et l'intelligence
Parfois, la difficulté et le nombre de questions sur un test de QI est sélectionné afin de donner des résultats distribués normales. Ou bien, les résultats des tests premières sont converties en valeurs de QI par leur adaptation à la distribution normale. Dans les deux cas, il est le résultat délibéré de la construction d'essai ou marquer interprétation qui mène à des scores de QI étant distribuées normalement pour la majorité de la population. Cependant, la question de savoir si l'intelligence elle-même est normalement distribué est plus complexe, car l'intelligence est une variable latente, donc sa distribution ne peut être observée directement.
équation de diffusion
La fonction de densité de probabilité de la distribution normale est étroitement liée à la (homogène et isotrope)équation de diffusion et donc également à la ??quation de la chaleur.Cetteéquation différentielle partielledécrit l'évolution dans le temps d'une fonction de masse de densité sous diffusion.En particulier, la fonction de densité de probabilité
pour la distribution normale avec valeur 0 et de variance attendustsatisfait l'équation de diffusion:
Si la masse densité au moment t = 0 est donnée par un Dirac, ce qui signifie essentiellement que toute la masse est d'abord concentré en un seul point, alors la fonction de masse densité au moment t aura la forme de la fonction normale de densité de probabilité avec une variance croissante linéairement avec t . Cette connexion est pas un hasard: la diffusion est due à un mouvement brownien qui est mathématiquement décrite par un processus de Wiener, et un tel processus au moment t se traduira également par une distribution normale avec une variance croissante linéairement avec t .
Plus généralement, si la masse-densité initiale est donnée par une fonction ?? (x), puis la masse densité au momenttsera donnée par laconvolution de ?? et une fonction normale de densité de probabilité.
Approximations numériques de la distribution normale et son cdf
La distribution normale est largement utilisé dans le calcul scientifique et statistique. Par conséquent, il a été mis en ??uvre de diverses manières.
Le GNU Scientific Library calcule les valeurs de la fonction de répartition normale standard en utilisant des approximations par morceaux en fonctions rationnelles. Une autre méthode d'approximation utilise des polynômes du troisième degré sur des intervalles . L'article sur le langage de programmation de la Colombie-Britannique donne un exemple de la façon de calculer la cdf dans GNU bc.
Génération d'écarts de l'unité normale se fait normalement en utilisant la méthode de Box-Muller de choisir un angle uniforme et un rayon exponentielle puis transformer à (normalement distribué) x et y coordonnées. Si journaux, cos ou le péché sont chers alors une alternative simple est de simplement résumer 12 uniforme (0,1) et écarte soustraire 6 (la moitié de 12). Ceci est tout à fait utilisable dans de nombreuses applications. La somme de plus de 12 valeurs est choisi car cela donne un écart d'exactement un. Le résultat est limité à la plage (-6,6) et a une densité qui est un 12-section onzième ordre approximation polynomiale à la distribution normale.
Une méthode qui est beaucoup plus rapide que la Box-Muller transformer, mais qui est encore exacte est le soi-disant algorithme Ziggurat développé par George Marsaglia. Dans environ 97% de tous les cas, il utilise seulement deux nombres aléatoires, un entier aléatoire et un uniforme aléatoire, une multiplication et un test, si. Seulement dans 3% des cas où la combinaison de ces deux chutes à l'extérieur du "noyau de la ziggourat" une sorte de rejet d'échantillonnage en utilisant les logarithmes, exponentielles et des nombres aléatoires plus uniformes doit être employé.
Il ya aussi quelques recherches sur le lien entre le jeûne Hadamard transformer et la distribution normale depuis le transformer emploie un peu addition et la soustraction et par les théorème de la limite des nombres aléatoires centrales de presque toute distribution sera transformé en la distribution normale. A cet égard, une série de transformées de Hadamard peut être combiné avec des permutations aléatoires pour activer des ensembles de données arbitraires dans un ensemble de données à distribution normale.
En Microsoft Excel la fonction NORMSDIST () calcule la fonction de répartition de la distribution normale standard, et NORMSINV () calcule sa fonction inverse. Par conséquent, NORMSINV (RAND ()) est une façon précise mais lente de générer des valeurs de la distribution normale standard, en utilisant le principe de la transformation inverse échantillonnage.
Bagatelles
- La dernière série de10 billets en deutsche marks en vedetteCarl Friedrich Gausset un graphique et la formule de la fonction normale de densité de probabilité.
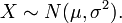
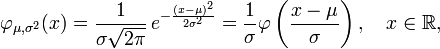
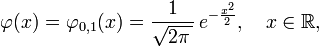

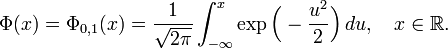
![\ Phi (x) = \ frac {1} {2} \ Bigl [1 + \ {operatorname erf} \ Bigl (\ frac {x} {\ sqrt {2}} \ bigr) \ bigr], \ quad x \ dans \ mathbb {R},](../../images/108/10890.png)
![\ Phi _ {\ mu, \ sigma ^ 2} (x) = \ frac {1} {2} \ Bigl [1 + \ {operatorname erf} \ Bigl (\ frac {x \ mu} {\ sigma \ sqrt { 2}} \ bigr) \ bigr], \ quad x \ in \ mathbb {R}.](../../images/108/10891.png)
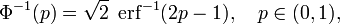
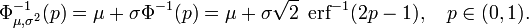



![\ Begin {align} m_x (t) et {} = \ mathrm {E} \ left [\ {exp (TX)} \ right] \\ & {} = \ int _ {- \ infty} ^ {\ infty} \ frac {1} {\ sigma \ sqrt {2 \ pi}} \ exp {\ left (- \ frac {(x - \ mu) ^ 2} {2 \ sigma ^ 2} \ right)} \ {exp (tx )} \, dx \\ & {} = \ exp {\ left (\ mu t + \ frac {\ sigma ^ 2 t ^ 2} {2} \ right)} \ end {align}](../../images/109/10904.png)
![\ Begin {align} \ chi_X (t; \ mu, \ sigma) et {} = m_x (it) = \ mathrm {E} \ left [\ exp (ce X) \ right] \\ & {} = \ int_ {- \ infty} ^ {\ infty} \ frac {1} {\ sigma \ sqrt {2 \ pi}} \ exp \ gauche (- \ frac {(x - \ mu) ^ 2} {2 \ sigma ^ 2 } \ right) \ exp (itx) \, dx \\ & {} = \ exp \ left (i \ mu t - \ frac {\ sigma ^ 2 t ^ 2} {2} \ right). \ End {align}](../../images/109/10907.png)