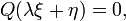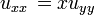??quation aux d??riv??es partielles
Saviez-vous ...
SOS Enfants, un organisme de bienfaisance de l'??ducation , a organis?? cette s??lection. Visitez le site Web d'enfants SOS au http://www.soschildren.org/
En math??matiques , ??quations aux d??riv??es partielles (PDE) sont un type de l'??quation diff??rentielle , soit un relation impliquant un inconnu fonction (ou fonctions) de plusieurs variables ind??pendantes et de son (resp.) de leur d??riv??es partielles par rapport aux variables. ??quations aux d??riv??es partielles sont utilis??es pour formuler, et ainsi aider ?? la solution de probl??mes impliquant des fonctions de plusieurs variables; telles que la propagation des sons ou de la chaleur , ??lectrostatique, l'??lectrodynamique, l'??coulement du fluide, ??lasticit??. Fait int??ressant, les ph??nom??nes physiques apparemment distinctes peuvent avoir des formulations math??matiques identiques, et donc ??tre r??gi par la m??me dynamique sous-jacente.
Introduction
Une ??quation diff??rentielle partielle est relativement simple
Cette relation implique que les valeurs u (x, y) sont ind??pendants de x. D'o?? la solution g??n??rale de cette ??quation est
o?? f est une fonction arbitraire (diff??rentiable) de y. L'analogue ??quation diff??rentielle ordinaire est
ce qui a pour solution
o?? c est ne importe quel valeur constante (ind??pendant de x). Ces deux exemples montrent que des solutions g??n??rales d'??quations diff??rentielles ordinaires impliquent constantes arbitraires, mais les solutions d'??quations aux d??riv??es partielles impliquent des fonctions arbitraires. Une solution d'une ??quation diff??rentielle partielle est g??n??ralement pas uniques; conditions suppl??mentaires doivent g??n??ralement ??tre sp??cifi??s sur la limite de la r??gion o?? la solution est d??finie. Par exemple, dans l'exemple simple ci-dessus, la fonction 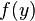 peut ??tre d??termin?? si
peut ??tre d??termin?? si 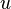 est sp??cifi?? sur la ligne
est sp??cifi?? sur la ligne  .
.
Existence et unicit??
Bien que la question de l'existence et l'unicit?? de solutions d'??quations diff??rentielles ordinaires a une r??ponse tr??s satisfaisante avec le Th??or??me de Cauchy-Lipschitz, qui est loin d'??tre le cas pour les ??quations aux d??riv??es partielles. Il ya un th??or??me g??n??ral (la Th??or??me de Cauchy-Kovalevskaya) qui indique que le Probl??me de Cauchy pour toute ??quation diff??rentielle partielle qui est analytique dans la fonction inconnue et ses d??riv??s ont une solution analytique unique. Bien que ce r??sultat peut appara??tre pour r??gler l'existence et l'unicit?? de solutions, il ya des exemples d'??quations aux d??riv??es partielles lin??aires dont les coefficients ont d??riv??s de toutes les commandes (qui sont cependant pas analytique), mais qui ne ont pas de solutions ?? tous: voir Lewy (1957). M??me si la solution d'une ??quation diff??rentielle partielle existe et est unique, elle peut n??anmoins avoir des propri??t??s ind??sirables.
Un exemple de comportement pathologique est la s??quence des probl??mes de Cauchy (n) d??pendant de la ??quation de Laplace
avec conditions initiales
o?? n est un entier. La d??riv??e de u par rapport ?? y se approche de 0 uniform??ment en x lorsque n augmente, mais la solution est
Cette solution tend vers l'infini, si nx est pas un multiple entier de π pour chaque valeur de y non nul. Le probl??me de Cauchy pour l'??quation de Laplace est appel??e mal pos?? ou non bien pos??, car la solution ne d??pend pas de mani??re continue sur les donn??es du probl??me. Ces probl??mes mal pos??s ne sont g??n??ralement pas satisfaisante pour les applications physiques.
Notation et exemples
Dans PDE, il est courant pour d??signer d??riv??es partielles ?? l'aide des indices. C'est:
Surtout dans (math??matique) la physique, on pr??f??re souvent usage de del (qui en coordonn??es cart??siennes est ??crit 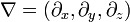 pour les d??riv??es spatiales et un point
pour les d??riv??es spatiales et un point 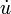 pour les d??riv??s de temps, par exemple, pour ??crire le ??quation d'onde (voir ci-dessous)
pour les d??riv??s de temps, par exemple, pour ??crire le ??quation d'onde (voir ci-dessous)
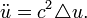 (Notation math??matique)
(Notation math??matique)
 (Notation de la physique)
(Notation de la physique)
Equation de la chaleur dans une dimension de l'espace
L'??quation de conduction de la chaleur dans une dimension pour un corps homog??ne a la forme
o?? u (t, x) est la temp??rature, et α est une constante positive qui d??crit la vitesse de diffusion. Le probl??me de Cauchy pour cette ??quation consiste ?? sp??cifier 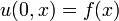 , O?? f (x) est une fonction arbitraire.
, O?? f (x) est une fonction arbitraire.
Solutions g??n??rales de l'??quation de la chaleur peuvent ??tre trouv??s par le proc??d?? de s??paration des variables. Quelques exemples figurent dans le article ??quation de la chaleur. Ils sont des exemples de S??ries de Fourier pour p??riodique f et Transform??es de Fourier pour non p??riodique f. Utilisation de la transform??e de Fourier, une solution g??n??rale de l'??quation de la chaleur a la forme
o?? F est une fonction arbitraire. Pour satisfaire ?? la condition initiale, F est donn??e par la transform??e de Fourier de f, ce est-
Si f repr??sente un tr??s petit mais intense source de chaleur, puis l'int??grale pr??c??dente peut ??tre approch??e par la la distribution delta, multipli?? par la r??sistance de la source. Pour une source dont la force est normalis??e ?? 1, le r??sultat est
et la solution r??sultante de l'??quation de la chaleur est
C'est un Gaussienne int??grante. Elle peut ??tre ??valu??e ?? obtenir
Ce r??sultat correspond ?? une densit?? de probabilit?? normale pour x avec une moyenne de 0 et de variance t 2α. L'??quation de la chaleur et similaires ??quations de diffusion sont des outils utiles pour ??tudier des ph??nom??nes al??atoires.
??quation d'onde dans une dimension spatiale
Le ??quation d'onde est une ??quation pour une fonction inconnue u (t, x) de la forme
Ici u peut d??crire le d??placement d'une cha??ne ??tir??e ?? partir de l'??quilibre, ou la diff??rence de pression d'air dans un tube, ou l'amplitude d'un champ ??lectromagn??tique dans un tube, et c est un nombre qui correspond ?? la vitesse de l'onde. Le probl??me de Cauchy pour cette ??quation consiste ?? prescrire le d??placement initial et la vitesse d'une cha??ne ou un autre support:
o?? f et g sont des fonctions arbitraires donn??s. La solution de ce probl??me est donn??e par la formule de d'Alembert:
Cette formule implique que la solution ?? (t, x) ne d??pend que des donn??es sur le segment de ligne initial qui est coup?? par le courbes caract??ristiques
qui sont tir??s vers l'arri??re de ce point. Ces courbes correspondent ?? des signaux qui se propagent ?? la vitesse c avant et en arri??re. Inversement, l'influence des donn??es ?? ne importe quel point sur la ligne initiale donn??e se propage ?? la vitesse finie c: il n'y a pas d'effet en dehors d'un triangle par ce point dont les c??t??s sont courbes caract??ristiques. Ce probl??me est tr??s diff??rent de la solution de l'??quation de chaleur, o?? l'effet d'un source ponctuelle appara??t (avec faible amplitude) instantan??ment ?? chaque point de l'espace. La solution donn??e ci-dessus est ??galement valable si t est n??gatif, et la formule explicite montre que la solution d??pend en douceur sur les donn??es: ?? la fois vers l'avant et vers l'arri??re probl??mes de Cauchy pour l'??quation d'onde sont bien pos??es.
Ondes sph??riques
Ondes sph??riques sont des ondes dont l'amplitude ne d??pend que de la distance r ?? partir d'un central radial source ponctuelle. Pour ces ondes, l'??quation d'onde tridimensionnelle prend la forme
Ceci est ??quivalent ??
et par cons??quent la quantit?? ru satisfait ?? l'??quation d'onde unidimensionnelle. Par cons??quent, une solution g??n??rale pour les ondes sph??riques a la forme
o?? F et G sont des fonctions totalement arbitraires. Rayonnement d'une antenne correspond au cas o?? G est identiquement nulle. Ainsi la forme d'onde transmise par une antenne a pas de distorsion dans le temps: le seul facteur de distorsion est 1 / r. Cette fonction de propagation des ondes non fauss??e ne est pas pr??sent se il ya deux dimensions spatiales.
??quation de Laplace en deux dimensions
Le ??quation de Laplace pour une fonction inconnue de deux variables φ est de la forme
Les solutions de l'??quation de Laplace sont appel??s fonctions harmoniques.
Connexion avec des fonctions
Les solutions de l'??quation de Laplace sont intimement li??es ?? des fonctions analytiques d'une variable complexe (fonctions holomorphes aka): les parties r??elle et imaginaire d'une fonction analytique sont des fonctions harmoniques conjugu??s: ils ont tous deux satisfont l'??quation de Laplace, et leurs gradients sont orthogonaux. Si f = u + iv, le Cauchy-Riemann ??quations Etat qui
et il se ensuit que
A l'inverse, compte tenu de toute fonction harmonique, ce est la partie r??elle d'une fonction analytique, au moins localement. Les d??tails sont donn??s dans ??quation de Laplace.
Un probl??me typique de la valeur limite
Un probl??me typique pour l'??quation de Laplace est de trouver une solution qui satisfait des valeurs arbitraires sur la limite d'un domaine. Par exemple, nous pouvons rechercher une fonction harmonique qui prend les valeurs u (θ) sur un cercle de rayon d'un. La solution est donn??e par Poisson:
P??trovsky (1967, p. 248) montre comment cette formule peut ??tre obtenu en additionnant une s??rie de Fourier de φ. Si r <1, les d??riv??s de φ peuvent ??tre calcul??es en diff??renciant sous le signe, et on peut v??rifier que φ est analytique, m??me si u est continue mais pas n??cessairement diff??rentiables. Ce comportement est typique des solutions de ??quations aux d??riv??es partielles elliptiques: les solutions peuvent ??tre beaucoup plus lisse que les donn??es sur les limites. Ceci est en contraste avec les solutions de la ??quation d'onde, et plus g??n??rale ??quations aux d??riv??es partielles hyperboliques, qui ont g??n??ralement pas plus de d??riv??s que les donn??es.
??quation d'Euler-Tricomi
Le ??quation d'Euler-Tricomi est utilis?? dans l'enqu??te de ??coulement transsonique. C'est
??quation d'advection
Le ??quation d'advection d??crit le transport d'un scalaire conserv??e  dans un champ de vitesse
dans un champ de vitesse 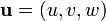 . C'est:
. C'est:
Si le champ de vitesse est sol??no??dal (ce est- 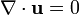 ), L'??quation peut ??tre simplifi??e pour
), L'??quation peut ??tre simplifi??e pour
L'une ??quation d'advection de flux constant dimensions 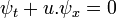 (O??
(O?? 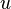 est constant) est commun??ment d??nomm?? probl??me porcherie. Si
est constant) est commun??ment d??nomm?? probl??me porcherie. Si 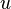 ne est pas constant et ??gal ??
ne est pas constant et ??gal ??  l'??quation est appel??e ??quation de Burgers.
l'??quation est appel??e ??quation de Burgers.
L'??quation de Ginzburg-Landau
Le L'??quation de Ginzburg-Landau est utilis?? dans la mod??lisation de la supraconductivit?? . C'est
o?? 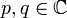 et
et 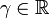 sont des constantes et
sont des constantes et  est l'unit?? imaginaire.
est l'unit?? imaginaire.
L'??quation Dym
Le Dym ??quation est nomm?? pour Dym Harry et se produit ?? l'??tude de solitons. C'est
D'autres exemples
Le ??quation de Schr??dinger est un PDE au c??ur de non-relativistes m??canique quantique . Dans le Approximation BKW ce est le ??quation de Hamilton-Jacobi.
Sauf pour l'??quation Dym et l'??quation de Ginzburg-Landau, les ??quations ci-dessus sont lin??aires dans le sens o?? elles peuvent ??tre ??crites sous la forme Au = f pour une donn??e lin??aire op??rateur A et une fonction donn??e f. Autres ??quations non lin??aires importants comprennent les ??quations de Navier-Stokes d??crivant l'??coulement des fluides, et Einstein ??quations du champ de la relativit?? g??n??rale .
M??thodes pour r??soudre les EDP
Proc??d?? selon la s??paration des variables donnera des solutions particuli??res d'un PDE lin??aire sur des domaines tr??s simples tels que des rectangles qui peuvent satisfaire les conditions initiales ou limites. Parce que toute superposition de solutions d'un nouveau PDE lin??aire est une solution, les solutions particuli??res peuvent ensuite ??tre combin??s pour obtenir des solutions plus g??n??rales. Si le domaine est fini ou p??riodique, une somme infinie de solutions telles qu'un s??rie de Fourier est appropri??e, mais une int??grale de solutions telles que la int??grale de Fourier est g??n??ralement requise pour les domaines infinite. La solution pour une source ponctuelle de l'??quation de la chaleur donn??e ci-dessus est un exemple d'utilisation d'une int??grale de Fourier.
Probl??mes de valeur initiale de limite
Beaucoup de probl??mes de physique math??matique sont formul??s comme des probl??mes de valeur initiale de limites.
Corde vibrante
Si la cha??ne est tendue entre deux points o?? x = 0 et x = L et U d??signe l'amplitude du d??placement de la cha??ne, puis u satisfait l'??quation des ondes ?? une dimension dans la r??gion o?? 0 <x <L et t est illimit?? . Depuis la cha??ne est attach?? aux extr??mit??s, u doit ??galement satisfaire les conditions aux limites
ainsi que les conditions initiales
Proc??d?? de s??paration des variables de l'??quation d'onde
conduit ?? des solutions de la forme
o??
o?? la constante k doit ??tre d??termin??e. Les conditions aux limites impliquerait alors que X est un multiple du p??ch?? kx, et k doivent avoir la forme
o?? n est un entier. Chaque terme de la somme correspond ?? un mode de vibration de la corde. Le mode avec n = 1 est appel?? le mode fondamental, et les fr??quences des autres modes sont tous des multiples de cette fr??quence. Ils forment la Overtone s??rie de la cha??ne, et ils sont la base de l'acoustique musicale. Les conditions initiales peuvent alors ??tre remplies par f et g soit comme des sommes infinies de ces modes. Instruments ?? vent correspondent g??n??ralement ?? des vibrations d'une colonne d'air avec une extr??mit?? ouverte et une extr??mit?? ferm??e. Les conditions aux limites correspondantes sont
Proc??d?? de s??paration des variables peut ??galement ??tre appliqu??e dans ce cas, et cela conduit ?? une s??rie d'harmoniques impairs.
Le probl??me de ce type g??n??ral est r??solu en Th??orie de Sturm-Liouville.
Membrane vibrante
Si une membrane est tendue sur une courbe C qui forme la limite d'un domaine D dans le plan, ses vibrations sont r??gies par l'??quation des ondes
si t> 0 et (x, y) est en d??veloppement. La condition limite est  si
si 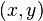 est le
est le 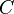 . Proc??d?? de s??paration des variables conduit ?? la forme
. Proc??d?? de s??paration des variables conduit ?? la forme
qui ?? son tour doit satisfaire
Cette derni??re ??quation est appel?? le Helmholtz ??quation. La constante k doit ??tre d??termin??e afin de permettre un v non n??gligeable pour satisfaire la condition aux limites sur C. De telles valeurs de k 2 sont appel??s les valeurs propres du Laplacien en D, et les solutions sont associ??es les fonctions propres du Laplacien par D. La th??orie de Sturm-Liouville peut ??tre ??tendue ?? ce probl??me elliptique valeur propre (Jost, 2002).
Il n'y a pas en g??n??ral de m??thodes applicables pour r??soudre des ??quations aux d??riv??es partielles non lin??aires. Pourtant, existence et unicit?? des r??sultats (tels que le Th??or??me de Cauchy-Kowalevski) sont souvent possible, comme le sont les preuves de propri??t??s qualitatives et quantitatives importantes de solutions (obtenir ces r??sultats est une partie importante de l'analyse ). Solution informatique pour les ??quations aux d??riv??es partielles non lin??aires, le M??thode split-??tape, exister pour ??quations sp??cifiques comme l'??quation de Schr??dinger non lin??aire.
N??anmoins, certaines techniques peuvent ??tre utilis??es pour plusieurs types d'??quations. Le h-principe est la m??thode la plus puissante pour r??soudre ??quations sousd??termin??s. Le Th??orie Riquier-Janet est une m??thode efficace pour obtenir des informations sur de nombreux analytique syst??mes surd??termin??s.
Le Proc??d?? de caract??ristiques ( Similarit?? m??thode de transformation) peut ??tre utilis?? dans certains cas tr??s particuliers pour r??soudre des ??quations aux d??riv??es partielles.
Dans certains cas, une PDE peut ??tre r??solu gr??ce ?? une analyse de perturbation, dans lequel la solution est consid??r??e comme une correction ?? une ??quation d'une solution connue. Alternatives sont techniques d'analyse num??rique de la simple sch??mas aux diff??rences finies ?? la plus mature multigrille et m??thodes d'??l??ments finis. De nombreux probl??mes int??ressants dans la science et l'ing??nierie sont r??solus de cette mani??re en utilisant des ordinateurs , parfois haute performance superordinateurs.
Classification
Quelques ??quations aux d??riv??es partielles lin??aire, second ordre peuvent ??tre class??s comme parabolique, hyperbolique ou elliptique. D'autres, comme le ??quation d'Euler-Tricomi ont diff??rents types dans diff??rentes r??gions. La classification fournit un guide pour se approprier conditions initiales et aux limites, et de la douceur des solutions.
??quations du second ordre
Supposant 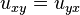 , Le PDE g??n??rale de second ordre ?? deux variables ind??pendantes a la forme
, Le PDE g??n??rale de second ordre ?? deux variables ind??pendantes a la forme
o?? les coefficients A, B, C etc. peut d??pendre de x et y. Cette forme est analogue ?? l'??quation d'une section conique:
Tout comme on classe les sections coniques en parabolique, hyperbolique et elliptique sur la base du discriminant 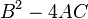 , La m??me chose peut ??tre fait pour un PDE second ordre ?? un moment donn??.
, La m??me chose peut ??tre fait pour un PDE second ordre ?? un moment donn??.
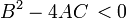 : Solutions de EDP elliptiques sont aussi lisses que les coefficients permettent, ?? l'int??rieur de la r??gion o?? l'??quation et les solutions sont d??finis. Par exemple, les solutions de l'??quation de Laplace sont analytiques dans le domaine o?? ils sont d??finis, mais les solutions peuvent prendre des valeurs limites qui ne sont pas lisses. Le mouvement d'un fluide ?? des vitesses subsoniques peut ??tre approch??e avec EDP elliptiques, et l'??quation d'Euler-Tricomi est elliptique o?? x <0.
: Solutions de EDP elliptiques sont aussi lisses que les coefficients permettent, ?? l'int??rieur de la r??gion o?? l'??quation et les solutions sont d??finis. Par exemple, les solutions de l'??quation de Laplace sont analytiques dans le domaine o?? ils sont d??finis, mais les solutions peuvent prendre des valeurs limites qui ne sont pas lisses. Le mouvement d'un fluide ?? des vitesses subsoniques peut ??tre approch??e avec EDP elliptiques, et l'??quation d'Euler-Tricomi est elliptique o?? x <0. 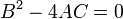 qui sont les ??quations: parabolique ?? chaque point peut ??tre transform?? en une forme analogue ?? l'??quation de la chaleur par un changement de variables ind??pendantes. Solutions lisser les variables transform??es de temps augmente. L'??quation d'Euler-Tricomi a type parabolique sur la ligne o?? x = 0.
qui sont les ??quations: parabolique ?? chaque point peut ??tre transform?? en une forme analogue ?? l'??quation de la chaleur par un changement de variables ind??pendantes. Solutions lisser les variables transform??es de temps augmente. L'??quation d'Euler-Tricomi a type parabolique sur la ligne o?? x = 0.  : ??quations hyperboliques conservent tous les discontinuit??s de fonctions ou de d??riv??s dans les donn??es initiales. Un exemple est le ??quation d'onde. Le mouvement d'un fluide ?? des vitesses supersoniques peut ??tre approch??e avec les syst??mes hyperboliques, et l'??quation d'Euler-Tricomi est hyperbolique o?? x> 0.
: ??quations hyperboliques conservent tous les discontinuit??s de fonctions ou de d??riv??s dans les donn??es initiales. Un exemple est le ??quation d'onde. Le mouvement d'un fluide ?? des vitesses supersoniques peut ??tre approch??e avec les syst??mes hyperboliques, et l'??quation d'Euler-Tricomi est hyperbolique o?? x> 0.
Si il ya des variables ind??pendantes n X 1, X 2, ..., x n, une ??quation lin??aire partielle diff??rentiel g??n??ral de second ordre a la forme
La classification d??pend de la signature des valeurs propres de la matrice de coefficients.
- Elliptic: Les valeurs propres sont tous positifs ou n??gatifs.
- Antenne: Les valeurs propres sont tous positifs ou tous n??gatifs, sauf un qui est nul.
- Hyperbolique: Il ya une seule valeur propre n??gatif et tout le reste sont positifs, ou il ya une seule valeur propre positive et tout le reste sont n??gatifs.
- Ultrahyperbolic: Il ya plus d'une valeur propre positive et plus d'une valeur propre n??gative, et il n'y a pas de valeurs propres z??ro. Il ne est que th??orie limit??e pour les ??quations ultrahyperbolic (Courant et Hilbert, 1962).
Syst??mes d'??quations du premier ordre et surfaces caract??ristiques
La classification des ??quations aux d??riv??es partielles peut ??tre ??tendue ?? des syst??mes d'??quations du premier ordre, o?? l'inconnue u est maintenant un vecteur ?? m composantes, et les matrices de coefficients 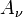 sont m par m matrices pour
sont m par m matrices pour 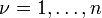 . L'??quation diff??rentielle partielle prend la forme
. L'??quation diff??rentielle partielle prend la forme
o?? le coefficient ν matrices A et le vecteur B peut d??pendre de x et u. Si une hypersurface S est donn??e dans la forme implicite
o?? φ a un gradient non nul, alors S est une surface caract??ristique de l'op??rateur L ?? un moment donn??, si la forme caract??ristique dispara??t:
L'interpr??tation de cette condition g??om??trique est la suivante: si les donn??es pour u sont pr??vues sur la surface S, alors il peut ??tre possible de d??terminer la d??riv??e normale de u sur S de l'??quation diff??rentielle. Si les donn??es sur S et l'??quation diff??rentielle d??terminer la d??riv??e normale de u sur S, alors S est non caract??ristique. Si les donn??es sur les S et l'??quation diff??rentielle ne d??terminent pas la d??riv??e normale de u sur S, alors la surface est caract??ristique, et l'??quation diff??rentielle limite les donn??es sur S: l'??quation diff??rentielle est interne ?? S.
- Un syst??me de premier ordre Lu = 0 est elliptique si aucune surface est caract??ristique pour L: les valeurs de u sur S et l'??quation diff??rentielle d??terminent toujours la d??riv??e normale de u sur S.
- Un syst??me de premier ordre est hyperbolique ?? un point se il ya une surface S comme-spatiale avec ξ normale ?? ce point. Cela signifie que, compte tenu de tout vecteur non trivial orthogonal ?? η ξ, et un multiplieur scalaire λ, l'??quation
a 1, λ 2, ..., λ m de m racines r??elles. Le syst??me est strictement hyperbolique si ces racines sont toujours distinctes. L'interpr??tation g??om??trique de cette condition est la suivante: la forme caract??ristique Q (ζ) = 0 d??finit un c??ne (le c??ne normal) avec des coordonn??es homog??ne ζ. Dans le cas hyperbolique, ce c??ne a m feuilles, et l'axe ζ = λ ξ se ex??cute dans ces feuilles: il ne coupe pas l'un d'eux. Mais lorsqu'il est d??plac?? depuis l'origine par η, cet axe croise chaque feuille. Dans le cas elliptique, le c??ne normal n'a pas de feuilles r??els.
??quations de type mixte
Si un PDE a coefficients qui ne sont pas constant, il est possible qu'il ne appartenait ?? aucune de ces cat??gories, mais plut??t ??tre de type mixte. Un exemple simple mais important, ce est l'??quation d'Euler-Tricomi
qui est appel?? elliptique-hyperbolique car il est elliptique dans la r??gion x <0, hyperbolique dans la r??gion x> 0, et parabolique d??g??n??r??e sur la ligne x = 0.


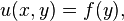
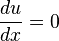
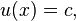
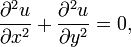
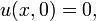
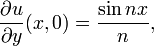

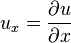
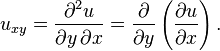
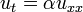
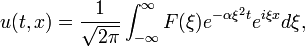

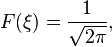

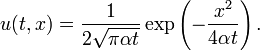
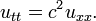
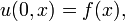
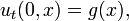
![u (t, x) = \ frac {1} {2} \ left [f (x-ct) + f (x + ct) \ right] + \ frac {1} {2c} \ {x int_-ct} ^ {x + ct} g (y) \, dy. \,](../../images/89/8985.png)

![u_ {tt} = c ^ 2 \ gauche [u_ {rr} + \ frac {2} {r} U_r \ right]. \,](../../images/89/8987.png)
![(Ru) _ {tt} = c ^ 2 \ left [(ru) _ {rr} \ right], \,](../../images/89/8988.png)
![u (t, r) = \ frac {1} {r} \ left [F (R-CT) + G (r + ct) \ right], \,](../../images/89/8989.png)
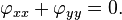
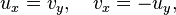

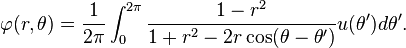
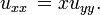
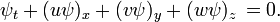
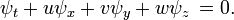
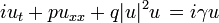
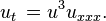

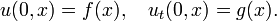

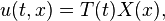

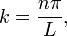
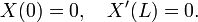
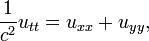
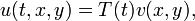
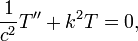
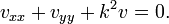
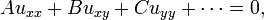
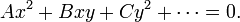
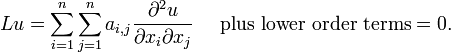
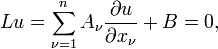
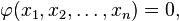
![Q \ left (\ frac {\ part \ varphi} {\ de x_1 partielle}, \ ldots, \ frac {\ part \ varphi} {\ de x_n partielle} \ right) = \ det \ left [\ sum _ {\ nu = 1 } ^ nA_ \ nu \ frac {\ partial \ varphi} {\ x_ partielle \ nu} \ right] = 0. \,](../../images/90/9030.png)