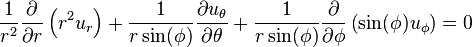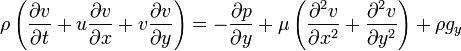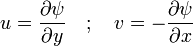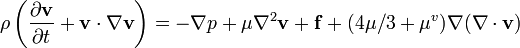??quations de Navier-Stokes
Saviez-vous ...
Cette s??lection de wikipedia a ??t?? choisi par des b??n??voles aidant les enfants SOS de Wikipedia pour cette s??lection Wikipedia pour les ??coles. Visitez le site Web d'enfants SOS au http://www.soschildren.org/
| M??canique des milieux continus |
|---|
 |
Lois
|
M??canique des solides
|
|
Rh??ologie
|
Les ??quations de Navier-Stokes, nomm?? d'apr??s Claude-Louis Navier et George Gabriel Stokes, d??crire le mouvement de substances fluides tels que les liquides et les gaz . Ces ??quations ??tablissent que les changements dans la dynamique des volumes infimes de liquide sont tout simplement la somme de dissipation forces de viscosit?? (similaires ?? friction), changements dans la pression, la gravit?? et d'autres forces qui agissent ?? l'int??rieur du fluide: une application de la deuxi??me loi de Newton ?? fluide.
Ils sont l'un des ensembles les plus utiles des ??quations parce qu'ils d??crivent la physique d'un grand nombre de ph??nom??nes d'int??r??t ??conomique et universitaire. Ils peuvent ??tre utilis??s pour mod??le m??t??o , les courants oc??aniques, les flux de l'eau dans un tuyau, l'??coulement autour d'un a??rodynamique (aile), et le mouvement des ??toiles ?? l'int??rieur d'une galaxie . En tant que tel, ces ??quations dans les deux formes complets et simplifi??s, sont utilis??s dans la conception des avions et des voitures, l'??tude de la circulation sanguine, la conception des centrales, l'analyse des effets de la pollution, etc. Coupl?? avec les ??quations de Maxwell qu'ils peuvent ??tre utilis?? pour mod??liser et d'??tude magn??tohydrodynamique.
Les ??quations de Navier-Stokes sont ??galement d'un grand int??r??t dans un sens purement math??matique. Assez ??tonnamment, compte tenu de leur large ??ventail d'utilisations pratiques, les math??maticiens ne ont pas encore prouv?? que dans trois solutions dimensions existent toujours ( existence), ou que, se ils existent, elles ne contiennent pas infinis, singularit??s ou des discontinuit??s (lissage). On les appelle les Navier-Stokes existence et r??gularit?? probl??mes. Le Clay Mathematics Institute a appel?? celui de la sept probl??mes ouverts plus importantes en math??matiques, et a offert un prix $ 1.000.000 pour une solution ou un contre-exemple.
Les ??quations de Navier-Stokes sont des ??quations diff??rentielles qui, contrairement ??quations alg??briques, ne ??tablissent pas explicitement une relation entre les variables d'int??r??t (par exemple, la vitesse et pression). Au contraire, ils ??tablissent des relations entre les taux de variation . Par exemple, les ??quations de Navier-Stokes pour simple cas d'un fluide id??ale (non visqueux) peut indiquer que l'acc??l??ration (le taux de variation de vitesse ) est proportionnelle ?? la gradient (un type de d??riv?? multivari??e) de pression.
Contrairement ?? ce qui est normalement vu dans m??canique des solides, les ??quations de Navier-Stokes dictent pas position, mais plut??t vitesse . Une solution des ??quations de Navier-Stokes se appelle un champ de champ de vitesse ou de l'??coulement, qui est une description de la vitesse du fluide en un point donn?? de l'espace et du temps. Une fois que le champ de vitesse est r??solu pour, d'autres quantit??s d'int??r??t (tels que le d??bit, la force de tra??n??e, ou le chemin d'une ??particule?? de fluide aura) peuvent ??tre trouv??s.
Propri??t??s
Non-lin??arit??
Les ??quations de Navier-Stokes sont non lin??aires ??quations aux d??riv??es partielles dans presque chaque situation r??elle (exceptions comprennent un flux dimensionnelle et rampante flux). La non-lin??arit?? rend la plupart des probl??mes difficiles ou impossibles ?? r??soudre et fait partie de la cause de turbulence.
La non-lin??arit?? est due ?? acc??l??ration de convection, qui est associ??e ?? une acc??l??ration de la variation de la vitesse en fonction du poste. Par cons??quent, tout ??coulement par convection, si turbulent ou non, entra??nera la non-lin??arit??, un exemple de convection mais laminaire (non turbulent) Flux serait le passage d'un fluide visqueux (par exemple l'huile) ?? travers une petite convergent buse. Ces flux, qu'ils soient exactement soluble ou non, peuvent souvent ??tre soigneusement ??tudi??e et comprise.
Turbulence
Turbulence est ?? la charge du temps chaotique comportement vu dans de nombreux ??coulements de fluides. Il est g??n??ralement admis que ce est en raison de la l'inertie du fluide dans son ensemble: l'aboutissement de temps d'acc??l??ration d??pendant et convective; De l?? d??coule o?? les effets inertiels sont petites ont tendance ?? ??tre laminaire (le Nombre de Reynolds quantifie combien le d??bit est affect??e par l'inertie). On croit, mais pas connu avec certitude, que les ??quations de Navier-Stokes mod??le turbulences correctement.
M??me si la turbulence est une exp??rience quotidienne, il est extr??mement difficile de trouver des solutions, de quantifier, ou caract??risent g??n??ral. A $ 1,000,000 prix a ??t?? offert en mai 2000 par le Clay Mathematics Institute ?? celui qui rend progr??s pr??liminaire vers une th??orie math??matique qui aidera ?? la compr??hension de ce ph??nom??ne.
La solution num??rique des ??quations de Navier-Stokes pour un ??coulement turbulent est extr??mement difficile, et en raison des significativement diff??rentes ??chelles m??lange de longueur qui sont impliqu??s dans l'??coulement turbulent, la solution stable de ce n??cessite une telle r??solution ?? mailles fines que le temps de calcul devient significativement impossible pour le calcul (voir Simulation num??rique directe). Des tentatives pour r??soudre l'??coulement turbulent en utilisant un solveur laminaire r??sulter typiquement dans une solution instable dans le temps, qui ne parvient pas ?? converger de mani??re appropri??e. Pour contrer cela, plusieurs approximations comme la moyenne par Reynolds ??quations de Navier-Stokes (RANS), compl??t??es par des mod??les de turbulence (comme le mod??le k-ε), sont utilis??s dans la dynamique des fluides computationnelle pratiques (CFD) des applications lors de la mod??lisation des ??coulements turbulents. Une autre technique pour r??soudre num??riquement l'??quation de Navier-Stokes est la simulation des grandes ??chelles (LES). Cette approche est math??matiquement plus cher que la m??thode RANS (dans le temps et la m??moire de l'ordinateur), mais produit de meilleurs r??sultats, puisqu'une partie des ??chelles caract??ristiques turbulentes sont explicitement r??solu.
Applicabilit??
Avec ??quations suppl??mentaires (par exemple, la conservation de la masse) et des conditions aux limites bien formul??es, les ??quations de Navier-Stokes semblent mod??liser mouvement fluide avec pr??cision; m??me ??coulements turbulents semblent (en moyenne) d'accord avec les observations du monde r??el.
Les ??quations de Navier-Stokes supposent que le fluide ??tudi?? est un continuum. ?? de tr??s petites ??chelles ou dans des conditions extr??mes, fluides r??els fabriqu??s ?? partir de mol??cules discr??tes va produire des r??sultats diff??rents de fluides continus mod??lis??s par les ??quations de Navier-Stokes. En fonction de la Nombre de Knudsen du probl??me, la m??canique statistique ou peut-??tre m??me dynamique mol??culaire peuvent ??tre une approche plus appropri??e.
Une autre limitation est tout simplement la nature complexe des ??quations. Temps formulations test??es existent pour les familles de fluide commun, mais l'application des ??quations de Navier-Stokes aux familles moins courantes tend ?? conduire ?? des formulations tr??s complexes qui sont un domaine de recherche en cours. Pour cette raison, les ??quations de Navier-Stokes sont g??n??ralement ??crites pour Fluides newtoniens.
D??rivation et la description
La d??rivation des ??quations de Navier-Stokes commence par la conservation de la masse, l'??lan et l'??nergie en cours d'??criture pour un volume de commande arbitraire. Dans un r??f??rentiel inertiel, la forme la plus g??n??rale des ??quations de Navier-Stokes finit par ??tre:
o?? 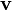 est la vitesse d'??coulement,
est la vitesse d'??coulement,  est la densit?? du fluide, p est la pression,
est la densit?? du fluide, p est la pression,  est le ( d??viatorique) tenseur, et
est le ( d??viatorique) tenseur, et 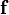 repr??sente les forces du corps (par unit?? de volume) agissant sur le fluide et
repr??sente les forces du corps (par unit?? de volume) agissant sur le fluide et  est le del op??rateur. Ce est une d??claration de la conservation du moment dans un fluide et ce est une application de la deuxi??me loi de Newton ?? un continuum. Cette ??quation est souvent ??crit en utilisant la d??riv?? de fond, ce qui rend plus ??vident que ce est une d??claration de la loi de Newton:
est le del op??rateur. Ce est une d??claration de la conservation du moment dans un fluide et ce est une application de la deuxi??me loi de Newton ?? un continuum. Cette ??quation est souvent ??crit en utilisant la d??riv?? de fond, ce qui rend plus ??vident que ce est une d??claration de la loi de Newton:
Le c??t?? gauche de l'??quation d??crit l'acc??l??ration, et peut ??tre compos?? d'effets d??pendant du temps ou de convection (??galement les effets de la non-coordonn??es inertielles si pr??sents). Le c??t?? droit de l'??quation est en effet d'une sommation de les forces du corps (telles que la pesanteur) et des d??riv??es spatiales des forces de surface (de pression et de stress).
Acc??l??ration convective

Une caract??ristique tr??s importante des ??quations de Navier-Stokes est la pr??sence de acc??l??ration convective. Ces termes d??signent le temps d'acc??l??ration d'un fluide ind??pendant par rapport ?? l'espace, et sont repr??sent??s par la quantit??:
Le gradient du vecteur de vitesse serait plus correctement ??tre r??dig??e avec le comme tenseur d??riv?? de 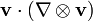 O??
O?? 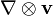 est le Matrice jacobienne de la vitesse par rapport ?? l'espace. Il ya quelques autres fa??ons de repr??senter convection:
est le Matrice jacobienne de la vitesse par rapport ?? l'espace. Il ya quelques autres fa??ons de repr??senter convection:
Le deuxi??me formulaire ci-dessus utilise le op??rateur d'advection et est commune (noter la diff??rence entre advection et convection - advection se r??f??re sp??cifiquement au transport d'un scalaire). La troisi??me forme a utiliser dans l'??coulement irrotationnel, o?? le boucle de la vitesse (appel?? tourbillon)  est absent.
est absent.
Ind??pendamment de ce type de fluide est trait??e, l'acc??l??ration convective est un effet non lin??aire. La convection est pr??sente dans la plupart des flux, exceptions comprennent rampante d??bit et incompressible dans une dimension.
Souligne
Le stress dans le fluide est repr??sent?? par la  et
et 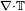 termes, ce sont des gradients de forces de surface, analogues ?? des contraintes dans un solide.
termes, ce sont des gradients de forces de surface, analogues ?? des contraintes dans un solide.  est appel?? le gradient de pression et provient de contraintes normales que l'on rencontre dans presque toutes les situations, dynamiques ou non.
est appel?? le gradient de pression et provient de contraintes normales que l'on rencontre dans presque toutes les situations, dynamiques ou non. 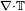 classiquement d??crit forces visqueuses; pour l'??coulement incompressible, ce ne est qu'un effet de cisaillement.
classiquement d??crit forces visqueuses; pour l'??coulement incompressible, ce ne est qu'un effet de cisaillement.
Fait int??ressant, que le gradient de pression pr??sente, elle-m??me pas la pression. L'effet du gradient de pression, ce est que le fluide se ??coule ?? partir de la haute pression ?? la basse pression.
Le terme de stress 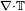 contient trop d'inconnues pour ??tre imm??diatement utilisable, donc la forme g??n??rale ci-dessus ne est pas directement applicable ?? des probl??mes pratiques. Pour cette raison, les hypoth??ses sur le comportement visqueux sp??cifique d'un fluide sont r??alis??s (bas??es sur des observations naturelles) et appliqu??s afin de pr??ciser cette quantit?? en termes de variables familiers, comme la vitesse. Par exemple, ce terme devient la quantit?? utile
contient trop d'inconnues pour ??tre imm??diatement utilisable, donc la forme g??n??rale ci-dessus ne est pas directement applicable ?? des probl??mes pratiques. Pour cette raison, les hypoth??ses sur le comportement visqueux sp??cifique d'un fluide sont r??alis??s (bas??es sur des observations naturelles) et appliqu??s afin de pr??ciser cette quantit?? en termes de variables familiers, comme la vitesse. Par exemple, ce terme devient la quantit?? utile  lorsque le fluide est suppos?? incompressible et Newtonien.
lorsque le fluide est suppos?? incompressible et Newtonien.
D'autres forces
 repr??sente ??autres?? ( la force du corps) des forces. G??n??ralement, ce ne est que la gravit?? , mais peut inclure d'autres domaines (comme ??lectromagn??tique). Dans un non inertiel syst??me de coordonn??es, d'autres ??forces?? telle que celle associ??e ?? coordonn??es de rotation peuvent ??tre ins??r??s.
repr??sente ??autres?? ( la force du corps) des forces. G??n??ralement, ce ne est que la gravit?? , mais peut inclure d'autres domaines (comme ??lectromagn??tique). Dans un non inertiel syst??me de coordonn??es, d'autres ??forces?? telle que celle associ??e ?? coordonn??es de rotation peuvent ??tre ins??r??s.
Souvent, ces forces peuvent ??tre repr??sent??s par la pente d'une certaine quantit?? scalaire. La gravit?? de la 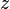 direction, par exemple, est le gradient de
direction, par exemple, est le gradient de  . Comme la pression ne se pr??sente comme un gradient, ce qui implique que la r??solution d'un probl??me sans effort corporel tel peut ??tre r??par?? afin d'inclure la force de corps en modifiant la pression.
. Comme la pression ne se pr??sente comme un gradient, ce qui implique que la r??solution d'un probl??me sans effort corporel tel peut ??tre r??par?? afin d'inclure la force de corps en modifiant la pression.
Autres ??quations
Les ??quations de Navier-Stokes sont strictement une d??claration de la conservation du moment. Afin de d??crire compl??tement l'??coulement du fluide, plus d'informations sont n??cessaires (combien d??pend des hypoth??ses retenues), ce qui peut inclure des donn??es de limite ( sans glissement, surface capillaire, etc.), la conservation de la masse, la conservation de l'??nergie, et / ou un ??quation d'??tat.
Quelles que soient les hypoth??ses de flux, une d??claration de la conservation de la masse est g??n??ralement n??cessaire. Ceci est r??alis?? ?? travers la masse ??quation de continuit??, donn??e dans sa forme la plus g??n??rale:
ou, en utilisant le d??riv?? de fond:
Ecoulement incompressible des fluides newtoniens
La grande majorit?? des travaux sur les ??quations de Navier-Stokes est fait en vertu d'un hypoth??se d'??coulement incompressible Fluides newtoniens. L'hypoth??se d'un fluide incompressible d??tient g??n??ralement bien, m??me lorsqu'il se agit d'un fluide "compressible", tel que l'air ?? la temp??rature ambiante (m??me lorsqu'il se ??coule jusqu'?? environ Mach 0,3). Prenant l'hypoth??se d'??coulement incompressible en compte et en supposant viscosit?? constante, les ??quations de Navier-Stokes vont lire (sous forme vectorielle):
f repr??sente ??autres?? les forces du corps (forces par unit?? de volume), tels que la gravit?? ou force centrifuge. Ce est bien la peine d'observer le sens de chaque terme:
Notez que seuls les termes convectifs sont non lin??aires pour l'??coulement newtonien incompressible. L'acc??l??ration convective est une acc??l??ration provoqu??e par un changement (??ventuellement en continu) dans la vitesse en position, par exemple l'acc??l??ration du fluide entrant dans une convergence buse. Bien que les particules de fluide individuels sont acc??l??r??s et par cons??quent sont en mouvement instable, le champ d'??coulement (une distribution de vitesse) ne sera pas forc??ment d??pendants du temps.
Une autre observation importante est que la viscosit?? est repr??sent?? par la vecteur de Laplace du champ de vitesse. Cela signifie que la viscosit?? newtonienne est la diffusion de l'impulsion, ce fonctionne de la m??me mani??re que le diffusion de la chaleur dans le voit ??quation de la chaleur (qui implique ??galement le Laplacien).
Si les effets de la temp??rature sont ??galement n??glig??s, la seule ??quation ??autre?? (en dehors des conditions initiales / limites) n??cessaire est l'??quation de continuit?? de masse. Dans l'hypoth??se incompressible, la densit?? est une constante et il en r??sulte que l'??quation simplifie ??:
Ce est plus pr??cis??ment une d??claration de la conservation du volume (voir divergence).
Ces ??quations sont couramment utilis??s dans les trois syst??mes de coordonn??es: Cart??sienne, cylindrique et sph??rique . Les ??quations cart??siennes d??coulent directement de l'??quation de vecteur ci-dessus, l'obtention d'??quations dans d'autres syst??mes de coordonn??es n??cessitera une changement de variables.
Les coordonn??es cart??siennes
??crit l'??quation vectorielle explicitement,
Notez que la gravit?? a ??t?? comptabilis??e comme une force du corps, et les valeurs de  d??pend de l'orientation de gravit?? par rapport ?? l'ensemble de coordonn??es choisi.
d??pend de l'orientation de gravit?? par rapport ?? l'ensemble de coordonn??es choisi.
L'??quation de continuit?? lit comme suit:
On notera que les composantes de la vitesse (les variables d??pendantes ?? r??soudre pour) sont 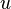 ,
, 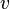 ,
, 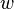 . Ce syst??me de quatre ??quations comprend la forme la plus couramment utilis?? et ??tudi??. Bien que relativement plus compact que les autres repr??sentations, ce est un syst??me non lin??aire des ??quations aux d??riv??es partielles pour lesquelles des solutions sont difficiles ?? obtenir.
. Ce syst??me de quatre ??quations comprend la forme la plus couramment utilis?? et ??tudi??. Bien que relativement plus compact que les autres repr??sentations, ce est un syst??me non lin??aire des ??quations aux d??riv??es partielles pour lesquelles des solutions sont difficiles ?? obtenir.
Coordonn??es cylindriques
Un changement de variables sur les ??quations cart??siennes donnera les ??quations de quantit?? de mouvement suivantes pour r, θ, et z:
Les composants de gravit?? ne seront g??n??ralement pas constantes, mais pour la plupart des applications, soit les coordonn??es sont choisis de sorte que les composantes de la gravit?? sont constantes, ou bien il est suppos?? que la gravit?? est compens??e par un champ de pression (par exemple, le d??bit dans le tuyau horizontal est trait??e normalement sans la gravit?? et sans gradient de pression vertical). L'??quation de continuit?? est:
Cette repr??sentation cylindrique des incompressibles ??quations de Navier-Stokes est le deuxi??me le plus souvent vu (le premier ??tant cart??sien ci-dessus). Les coordonn??es cylindriques sont choisis pour tirer parti de la sym??trie, de sorte qu'une composante de vitesse peut dispara??tre. Un cas tr??s commun est l'??coulement de r??volution, o?? il n'y a pas de vitesse tangentielle (  ) Et les quantit??s restantes sont ind??pendants de
) Et les quantit??s restantes sont ind??pendants de  :
:
Coordonn??es sph??riques
En coordonn??es sph??riques , le  ,
,  Et
Et 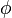 ??quations de momentum sont (noter la convention utilis??e:
??quations de momentum sont (noter la convention utilis??e: 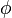 est colatitude):
est colatitude):
La continuit?? de masse va lire:
Ces ??quations pourraient ??tre (l??g??rement) simplifi??, par exemple, l'affacturage  des termes visqueux. Ceci ne est pas fait pour pr??server la structure du laplacien et les autres grandeurs.
des termes visqueux. Ceci ne est pas fait pour pr??server la structure du laplacien et les autres grandeurs.
Flux formulation de fonction
Prendre le friser les r??sultats de l'??quation de Navier-Stokes dans l'??limination de la pression. Cela est particuli??rement facile de voir si le d??bit cart??sienne 2D est suppos?? ( 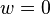 et aucune d??pendance de rien sur
et aucune d??pendance de rien sur 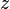 ), O?? les ??quations se r??duisent ??:
), O?? les ??quations se r??duisent ??:
Diff??rencier la premi??re par rapport ?? 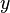 , La seconde par rapport ??
, La seconde par rapport ??  et en soustrayant les ??quations r??sultantes permettra d'??liminer toute pression et force potentielle. D??finition de la fonction de courant
et en soustrayant les ??quations r??sultantes permettra d'??liminer toute pression et force potentielle. D??finition de la fonction de courant  par
par
r??sultats dans la continuit?? de masse ??tant inconditionnellement satisfaits (??tant donn?? la fonction est continue des cours d'eau), puis incompressible dynamique 2D newtonienne et conservation de la masse se d??gradent dans une ??quation:
o??  est le (2D) op??rateur et biharmonique
est le (2D) op??rateur et biharmonique 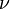 est le le viscosit?? cin??matique. Cette ??quation simple avec des conditions aux limites appropri??es d??crit l'??coulement du fluide 2D, en prenant la viscosit?? cin??matique seulement en tant que param??tre. On notera que l'??quation pour rampante r??sultats de d??bit lorsque le c??t?? gauche est suppos?? z??ro.
est le le viscosit?? cin??matique. Cette ??quation simple avec des conditions aux limites appropri??es d??crit l'??coulement du fluide 2D, en prenant la viscosit?? cin??matique seulement en tant que param??tre. On notera que l'??quation pour rampante r??sultats de d??bit lorsque le c??t?? gauche est suppos?? z??ro.
??coulements compressibles des fluides newtoniens
Il ya certains ph??nom??nes exceptionnels qui sont ??troitement li??s avec le fluide compressibilit??. L'un des exemples ??vidents est sonore . Description de ces ph??nom??nes n??cessite pr??sentation plus g??n??rale de l'??quation de Navier-Stokes qui tient compte de la compressibilit?? du fluide. Si la viscosit?? est suppos?? un, un mandat suppl??mentaire constante appara??t, comme indiqu?? ici:
o?? μ v est le deuxi??me coefficient de viscosit??. Elle est li??e ?? viscosit?? de volume ou viscosit?? apparente. Ce terme suppl??mentaire dispara??t pour un fluide incompressible, lorsque le divergence du flux est ??gal ?? 0.
Application ?? des probl??mes sp??cifiques
Les ??quations de Navier-Stokes, m??me lorsqu'il est r??dig?? express??ment pour les fluides sp??cifiques, sont plut??t de nature g??n??rique et leur bonne application ?? des probl??mes sp??cifiques peuvent ??tre tr??s diverses. Ce est en partie parce qu'il ya une grande vari??t?? de probl??mes qui peuvent ??tre mod??lis??s, allant d'aussi simple que la distribution de la pression statique aussi compliqu?? que l'??coulement polyphasique entra??n??e par la tension de surface .
G??n??ralement, application ?? des probl??mes sp??cifiques commence avec quelques hypoth??ses de flux et la formulation de condition initiale / limite, cela peut ??tre suivi par analyse ?? grande ??chelle de simplifier encore le probl??me. Par exemple, apr??s avoir assum?? constante, parall??lement, une pression nonconvective dimensions entra??n??e flux entre les plaques parall??les, le r??sultant ??chelle (dimension) probl??me aux limites est:
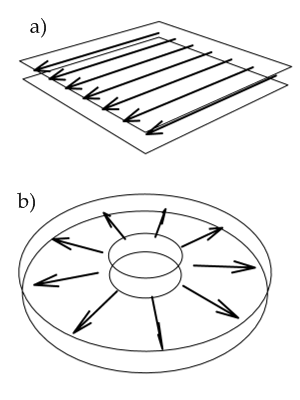
La condition limite est le aucune condition de glissement. Ce probl??me se r??sout facilement pour le champ d'??coulement:
Partir de ce point de plus grandes quantit??s d'int??r??t peuvent ??tre facilement obtenues, telles que la force de tra??n??e visqueuse ou d??bit net.
Des difficult??s peuvent survenir lorsque le probl??me devient un peu plus compliqu??. Une torsion apparemment modeste sur le flux parall??le ci-dessus serait l'??coulement radial entre des plaques parall??les; il se agit de la convection et donc la non-lin??arit??. Le champ de vitesse peut ??tre repr??sent??e par une fonction 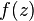 qui doit satisfaire:
qui doit satisfaire:
Cette ??quation diff??rentielle ordinaire est ce qui est obtenu lorsque les ??quations de Navier-Stokes sont ??crites et les hypoth??ses de flux appliqu??es (en outre, le gradient de pression est r??solu pour). Le terme non lin??aire en fait un probl??me tr??s difficile ?? r??soudre analytiquement (une longue solution implicite peut ??tre trouv?? qui implique int??grales elliptiques et racines de polyn??mes cubiques). Probl??mes avec l'existence r??elle de solutions surgissent R> 22,609 (environ), le param??tre R ??tant le Nombre de Reynolds avec ??chelles choisies de mani??re appropri??e. Ce est un exemple d'hypoth??ses de flux de perdre leur applicabilit??, et un exemple de la difficult?? de "haute" nombre de Reynolds se ??coule.

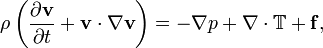
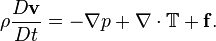

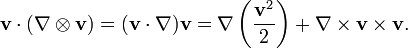

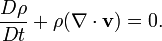

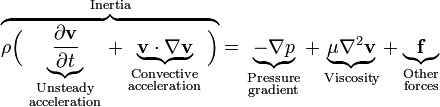


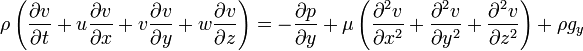
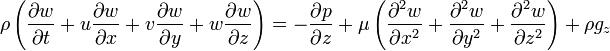

![\ Rho \ gauche (\ frac {\ U_r partielle} {\ t partielle} + U_r \ frac {\ de U_r partielle} {\ r partielle} + \ frac {u _ {\ theta}} {r} \ frac {\ U_r partielle } {\ partial \ theta} + u_z \ frac {\ U_r partielle} {\ z partielle} - \ frac {u _ {\ theta} ^ 2} {r} \ right) = - \ frac {\ p partielle} {\ r partielle} + \ mu \ left [\ frac {1} {r} \ frac {\ partial} {\ r partielle} \ left (r \ frac {\ de U_r partielle} {\ r partielle} \ right) + \ frac {1} {r ^ 2} \ frac {\ partial ^ 2 U_r} {\ partial \ theta ^ 2} + \ frac {\ de U_r partielle ^ 2} {\ z partielle ^ 2} - \ frac {U_r} {r ^ 2} - \ frac {2} {r ^ 2} \ frac {\ partial u _ {\ theta}} {\ partial \ theta} \ right] + \ rho g_r](../../images/181/18167.png)
![\ Rho \ gauche (\ frac {\ u _ {\ theta} partielle} {\ t partielle} + U_r \ frac {\ partial u _ {\ theta}} {\ r partielle} + \ frac {u _ {\ theta}} { r} \ frac {\ partial u _ {\ theta}} {\ partial \ theta} + u_z \ frac {\ partial u _ {\ theta}} {\ z partielle} + \ frac {U_r u _ {\ theta}} {r } \ right) = - \ frac {1} {r} \ frac {\ p partielle} {\ partial \ theta} + \ mu \ left [\ frac {1} {r} \ frac {\ partial} {\ partial r} \ left (r \ frac {\ partial u _ {\ theta}} {\ r partielle} \ right) + \ frac {1} {r ^ 2} \ frac {\ partial ^ 2 u _ {\ theta}} { \ partial \ theta ^ 2} + \ frac {\ partial ^ 2 u _ {\ theta}} {\ partial z ^ 2} + \ frac {2} {r ^ 2} \ frac {\ U_r partielle} {\ partial \ theta} - \ frac {u _ {\ theta}} {r ^ 2} \ right] + \ rho g _ {\ theta}](../../images/181/18168.png)
![\ Rho \ gauche (\ frac {\ u_z partielle} {\ t partielle} + U_r \ frac {\ de u_z partielle} {\ r partielle} + \ frac {u _ {\ theta}} {r} \ frac {\ u_z partielle } {\ partial \ theta} + u_z \ frac {\ u_z partielle} {\ z partielle} \ right) = - \ frac {\ p partielle} {\ z partielle} + \ mu \ left [\ frac {1} { r} \ frac {\ partial} {\ r partielle} \ left (r \ frac {\ u_z partielle} {\ r partielle} \ right) + \ frac {1} {r ^ 2} \ frac {\ partial ^ 2 u_z} {\ partial \ theta ^ 2} + \ frac {\ partial ^ 2 u_z} {\ z partielle ^ 2} \ right] + \ rho g_z](../../images/181/18169.png)

![\ Rho \ gauche (\ frac {\ U_r partielle} {\ t partielle} + U_r \ frac {\ de U_r partielle} {\ r partielle} + u_z \ frac {\ U_r partielle} {\ z partielle} \ right) = - \ frac {\ p partielle} {\ r partielle} + \ mu \ left [\ frac {1} {r} \ frac {\ partial} {\ r partielle} \ left (r \ frac {\ U_r partielle} {\ r partielle} \ right) + \ frac {\ partial ^ 2 U_r} {\ partial z ^ 2} - \ frac {} {U_r r ^ 2} \ right] + \ rho g_r](../../images/181/18172.png)
![\ Rho \ gauche (\ frac {\ u_z partielle} {\ t partielle} + U_r \ frac {\ de u_z partielle} {\ r partielle} + u_z \ frac {\ u_z partielle} {\ z partielle} \ right) = - \ frac {\ p partielle} {\ z partielle} + \ mu \ left [\ frac {1} {r} \ frac {\ partial} {\ r partielle} \ left (r \ frac {\ u_z partielle} {\ r partielle} \ right) + \ frac {\ partial ^ 2 u_z} {\ z partielle ^ 2} \ right] + \ rho g_z](../../images/181/18173.png)
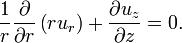
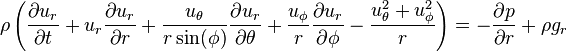
![\ Mu \ left [\ frac {1} {r ^ 2} \ frac {\ partial} {\ r partielle} \ left (r ^ 2 \ frac {\ de U_r partielle} {\ r partielle} \ right) + \ frac {1} {r ^ 2 \ sin (\ phi) ^ 2} \ frac {\ partial ^ 2 U_r} {\ partial \ theta ^ 2} + \ frac {1} {r ^ 2 \ sin (\ phi)} \ frac {\ partial} {\ partial \ phi} \ left (\ sin (\ phi) \ frac {\ U_r partielle} {\ partial \ phi} \ right) - 2 \ frac {U_r + \ frac {\ u_ partielle {\ phi}} {\ partial \ phi} + u _ {\ phi} \ lit b??b?? (\ phi)} {r ^ 2} + \ frac {2} {r ^ 2 \ sin (\ phi)} \ frac {\ partielle u _ {\ theta}} {\ partial \ theta} \ right]](../../images/181/18176.png)
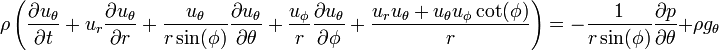
![\ Mu \ left [\ frac {1} {r ^ 2} \ frac {\ partial} {\ r partielle} \ left (r ^ 2 \ frac {\ partial u _ {\ theta}} {\ r partielle} \ right ) + \ frac {1} {r ^ 2 \ sin (\ phi) ^ 2} \ frac {\ partial ^ 2 u _ {\ theta}} {\ partial \ theta ^ 2} + \ frac {1} {r ^ 2 \ sin (\ phi)} \ frac {\ partial} {\ partial \ phi} \ left (\ sin (\ phi) \ frac {\ partial u _ {\ theta}} {\ partial \ phi} \ right) + \ frac {2 \ frac {\ U_r partielle} {\ partial \ theta} + 2 \ cos (\ phi) \ frac {\ partial u _ {\ theta}} {\ partial \ theta} - u _ {\ theta}} { r ^ 2 \ sin (\ phi) ^ 2} \ right]](../../images/181/18178.png)
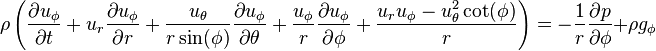
![\ Mu \ left [\ frac {1} {r ^ 2} \ frac {\ partial} {\ r partielle} \ left (r ^ 2 \ frac {\ partial u _ {\ phi}} {\ r partielle} \ right ) + \ frac {1} {r ^ 2 \ sin (\ phi) ^ 2} \ frac {\ partial ^ 2 u _ {\ phi}} {\ partial \ theta ^ 2} + \ frac {1} {r ^ 2 \ sin (\ phi)} \ frac {\ partial} {\ partial \ phi} \ left (\ sin (\ phi) \ frac {\ partial u _ {\ phi}} {\ partial \ phi} \ right) + \ frac {2} {r ^ 2} \ frac {\ U_r partielle} {\ \ partielle phi} - \ frac {u _ {\ phi} + 2 \ cos (\ phi) \ frac {\ partial u _ {\ theta} } {\ partial \ theta}} {r ^ 2 \ sin (\ phi) ^ 2} \ right]](../../images/181/18180.png)